Простое объяснение простоты

КДПВ с областями, которые нам придется посетить, чтобы ответить на ГЛАВНЫЙ вопрос.
Предисловие
Я часто слышал совет: сделай проще.
А что значит простой? Когда мы говорим, что X — простой, каковы наши ожидания от X? Когда мы говорим, что X проще Y — как мы это оцениваем?
Что проще:
“Небольшое предложение из пяти слов” или слово “Дезоксирибонуклеиновый”?
“6*5” или “481”?
Или так:
У вас есть экран настроек. Пять пунктов из них относятся к графике, другие пять к уведомлениям. Надо ли вам создавать отдельные пункты «графика» и «уведомления» в основном меню? Или оставить все 10 пунктов на одном экране? Что будет проще для пользователя?
Вы можете сказать, что это субъективно. Что это определяется неким “чувством простоты”, что для одного человека нечто может быть простым, а для другого сложным.
Окей, тогда скажите мне, зачем учитель тратит время на то, чтобы объяснить что-то проще? Зачем редактировать текст, пытаясь сделать его проще? Зачем программисты тратят время на ревью кода, пытаясь понять какое решение проще для понимания и расширения?
Если простота как-то коррелирует с нашей оценкой, то лучшая стратегия — убеждение. Давайте сделаем так, чтобы читатели поверили, что текст прост. Или коллеги, верили в то, что наше решение не сложно.
Изменит ли это качественно их взаимодействие с результатом нашей работы?
Нет.
Ваш текст не будет читаться проще от того, что его считают простым. С вашим кодом не станет легче работать, даже если все вокруг думают, что его сложность такая же, как у табуретки. Это не работает примерно по той же причине(ru, en), по которой вы не можете дать 5-ти своим друзьям по 1 кексу, если у вас есть только 2 коробки по 2 кекса в каждой. Даже если вы всей компанией будете год медитировать на то, что 2+2=5, печальную ситуацию с кексами это не изменит.
Еще раз. Есть объект, и какие-то его характеристики могут заставить вас думать(ru), что он простой. И если завтра ваша оценка изменится и остановится на отметке “сложный” — объекту на это будет плевать.
Можно прийти к выводу, что простота или сложность не зависят от наших ожиданий. Скорее наоборот, объект определяет то, какую характеристику мы ему дадим.
Мне хотелось понять, какой объект я ожидаю увидеть в реальности, если я убежден,(ru) что он прост. И наоборот, какие характеристики реального объекта заставляют меня думать, что он простой.
Зачем? Ну, может быть это сделает мою жизнь проще?)
Количество знаков: ~ 25k.
Если вы нашли непонятный или спорный момент — напишите об этом. Так вы поможете улучшить эту статью.
И ни в коем случае не верьте мне. Я не хочу, чтобы мои слова убеждали вас в моей правоте. Я хочу, чтобы их смысл убедил вас в его истинности.
- Оглавление. Каждая глава будет начинаться с него. В нем кратко перечислены вопросы, которые рассматриваются в главе, и даны ссылки для навигации на соответствующие подразделы.
- Ссылки на внешние ресурсы. Они представлены в виде *слово или фраза*(ссылки с laguage code) или обычных ссылок. Я старался сделать так, чтобы у вас был выбор, читать русский или английский источник. К сожалению, у меня не всегда получалось найти оба. Особенно это будет заметно во второй главе. Рунет беден на актуальную информацию по нейробиологии.
- Спойлер «Кратко». Находится сразу после названия подраздела главы. Его предназначение — упростить работу со статьей в случае, если вы ее уже прочитали. Вы можете использовать его для того, чтобы быстро ознакомиться со статьей. Но будьте осторожны! Во-первых, вы можете не понять, что там написано, без прочтения самого подраздела. Это сжатый тезиз, а не путь(ru, en) до него. Во вторыx, что еще более опасно — вам может показаться, что вы все поняли. Что такое ложное понимание и почему оно возникает будет объяснено в следующих главах.
- Спойлер «IT'S MATHEMATICS TIME». Используется, чтобы не пугать вас математическими выкладками. Он дублирует информацию, которая до него была представлена в виде текста, но более формальным образом.
На данный момент планируется 3 главы:
- Теоретически просто — эта глава посвящена формулировке вопроса и основным определениям с ним связанным. Вы находитесь здесь.
- Machine Ex Homo — глава, в которой мы посмотрим на наше сознание, начиная с верхнего поведенческого уровня и заканчивая нейронными связями в нашем . Глава написана и проходит редактуру.
- Просто чтение — посвящена чтению людьми любых моделей, будь то схемы, код, графы, текст. Это будет первая практическая глава в нашей серии, здесь мы будем применять наши знания, и смотреть на то, как должна быть структурирована информация для облегчения ее понимания. Глава в процессе написания.
Это не полный список вопросов, на которые я бы хотел найти ответ. Но начать я хочу с них.
Отдельно выйдет статья о том, почему я вообще занимаюсь этим вопросом. Скажем так, о мотивации автора, и о том, как он видит эту серию. Эта статья будет написана после первых трех глав.
Иногда я слышал слово «просто» в качестве аргумента в споре: «Я сделал так, потому что это проще!». Очень часто оппоненты пытались доказать, что «У них
Но когда я спрашивал людей, что по их мнению значит «просто», я слышал:
«Это субъективно». Или «Это common sense». Или «Ну, для каждого человека по-разному».
Меня приводило в замешательство то, что довольно умные люди очень долго спорят о вещи, которую они не могут точно определить и считают субъективной. Ведь если это вкусовщина, как например музыкальные предпочтения, то зачем они тратят на это время? Повторюсь, это были умные люди, и на холивары о музыкальных предпочтениях друг друга они время не тратили.
Я много об этом думал, и спустя год мне пришла в голову одна простая мысль: что если простота — это характеристика объекта, которую все же можно измерить? Это бы могло разрешить все споры и сэкономить огромное количество времени. И заверте…
Эта серия — результат тысяч часов работы по поиску и объединению информации. А так же сотен тысяч часов, потраченных людьми, чьи работы я для нее использовал.
На прочтение всей серии вы потратите пару часов. Десяток, если честно будете переходить по всем ссылкам.
Я уменьшил количество времени и сил, которое вы потратите для получения ответа на наш вопрос в сотни раз. И сэкономил вам время, которое ушло на то, чтобы правильно его задать.
Я не уверен, что это самое лучшее объяснение из возможных. Моя работа еще не закончена. Возможно, в процессе я пойму как его улучшить. На данный момент — это самое простое объяснение которое у меня есть.
Глава 1. Теоретически просто
В этой главе мы посмотрим на следующие темы:
- Как правильно задавать вопросы, и почему это важно? (Последовательность вопросов)
- Как связаны объекты, действия и их исполнители? (Простота в действии, Объективный субъективизм)
- Как определить сложность действия? (Простота в действии, Вероятно просто)
- Что такое системы и их модели и почему это удобный способ описания объектов? (Систематизация моделирования)
В конце главы мы немного поговорим о Бритве Оккама (Бегущий по лезвию). Статья о простоте смотрелась бы странно без упоминания этого принципа.
1.1 Последовательность вопросов
Характеристика «простой» может иметь два смысла:
1) Элементарный
2) Простой для каких-то действий
Нас интересует второй.
Наш следующий вопрос: Как оценить сложность действия и как связать ее с объектом?
Наше исследование начинается с вопроса. Задать вопрос правильно — это очень важно. Маленькое отступление:
— Окей, Deep Thought, каково ГЛАВНОЕ УСЛОВИЕ ПРОСТОТЫ?
— Надо подумать.
…
…
N миллионов лет спустя…
—
//По мотивам одной прекрасной книги
У нас есть ответ, но он ничего не дает. Вся информация о нем заключена в вопросе, а вопрос был не слишком конкретен. Мы не можем доказать, что 
Вопрос должен ограничивать область возможных ответов.
“Что такое просто?” — не слишком конкретный вопрос. Давайте уточним его. В начале статьи мы уже проделали часть этого пути:
Когда мы говорим что X — простой, что мы ожидаем от X?
По моим наблюдениям есть два основных кейса:
- X — это некий объект, не разбивающийся на составные части. Здесь слово «простой» можно заменить на слово «элементарный».

Это кирпич. И, в каком-то смысле, он — прост. - X — простой для выполнения c ним нужного нам действия. Например — диван простой если мы хотим на нем лежать, и сложный, если нам надо поднять его на девятый этаж.
Случай, когда объект элементарен — понятен. Но что делать, если нас интересует сложность в контексте действия?
Давайте подумаем. Мы совершаем действия с объектом.
В этом предложении есть три основных сущности:
- Действия — описание того, что происходит.
- Исполнители действий — скрываются под словом мы.
- Объекты — то, с чем совершается действие.
Тогда нас интересуют следующие вопросы:
- Как оценить простоту действия в зависимости от объекта, с которым оно выполняется?
- Какова связь между действием и его исполнителем?
На них мы и будем отвечать ниже.
1.2 Простота в действии
Сложность нашего действия — сумма сложностей вложенных в него действий.
Последовательность действий называется алгоритмом.
У действия есть результат — это изменение состояния системы, в которой было совершено действие.
Действия и объекты можно связать между собой с помощью понятия интерфейса. Интерфейс — это объект, который хранит информацию о том, какие действия возможны с объектом, его реализующим.
В отличии от алгоритмической сложности, мы не можем просто найти элементарные операции, и нам придется учитывать исполнителя наших действий.
Наш следующий вопрос — каково влияние исполнителя на действия?
Давайте посмотрим на действия.
Простота действия это нечто, что обратно зависит от его сложности. Чем сложнее действие, тем менее оно просто — это очевидно. Мы приходим к следующему вопросу:
Как определить сложность действия?
Что мы можем делать с действием? Мы можем разбивать его на последовательность других! Действие “прочитать статью” можно разбить на: “прочитать первый абзац”, “прочитать второй” и т.д. Их в свою очередь разложить как “прочитать первое предложение”, “прочитать второе”…
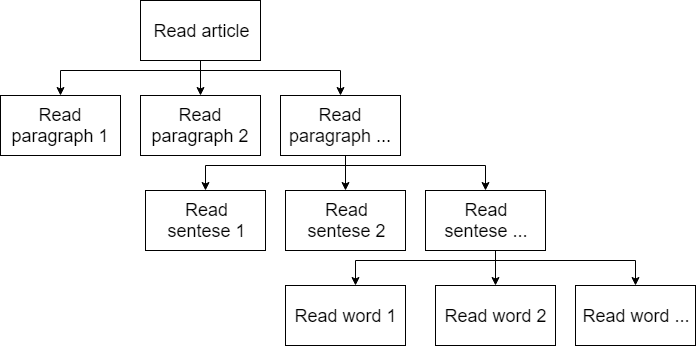
Подобным образом мы дойдем до действий, разница в сложности которых не будет для нас важна и не будет зависеть от объекта с которым оно выполняется (например, прочитать букву). Такие действия мы назовем элементарными.
Тогда сложность действия для конкретного объекта можно измерить в элементарных действиях, на которые оно разбивается.
Что еще характеризует действие?
Алгоритм
Описание последовательности действий, представляющих собой другое действие, я буду называть его алгоритмом(ru, en).
Действия эквивалентны когда одинаковы их алгоритмы.
Алгоритм может быть описан обобщенно, например:
Чтение: читать предложения, пока не кончится текст.
В таком виде чтение применимо ко многим текстам.
Однако, как вы понимаете, количество действий “читать предложения” при этом будет зависеть от количества предложений в тексте.
Результат
Действия выполняются не просто так, они к чему-то приводят. Так пусть у наших действий будут результаты!
Результат — это изменение состояния системы, в которой произошло действие. Вы нажали на выключатель, и его переход в состояние “включен” и загоревшийся на кухне свет — результат этого действия. Вы прочитали слово, и результат этого — изменение состояния вашего
Разные действия могут приводить к одному результату.
Связь с объектами
Вернемся к объектам. Как мы уже говорили, с ними можно совершать разные действия. Нам нужен способ понимать, для каких действий “предназначена” та или иная сущность.
Я начну с примера.
— И как мне тащить этот чемодан?
— У него ручка сбоку!
Ручка представляет собой полоску кожи с внешней стороны чемодана, которую прибили заклепками. Но нас в данном случае это не волнует. Нас волнует то, что на чемодане есть объект, за который можно держаться.
Все подобные объекты мы будем называть ручками. Они могут быть у чашки, двери, чемодана или ведра.
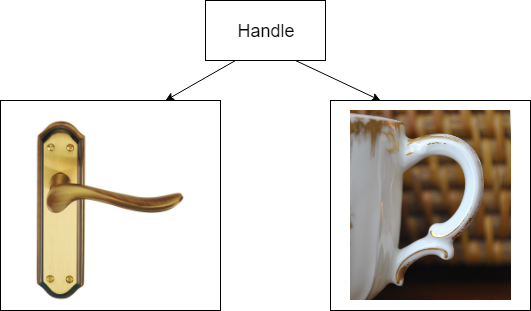
Мы пришли к тому, что у нас есть два описания ручки из примера:
- Как полоски кожи, прибитой заклепками к чемодану.
- Как концепции предмета за который можно взяться.
Первое — это описание реализации (en).
Второе — описание интерфейса.
Интерфейс — это объект, который хранит информацию о том, какими способами можно взаимодействовать с объектом его реализующим.
Зачем они нужны? Все просто: чаще всего нас не интересует как реализован объект.
Когда мы хотим включить свет — мы ищем переключатель, и нам не важно как он работает, нам важно лишь то, что мы можем переключить его состояние вкл/выкл.
Когда мы видим кнопку, мы уже знаем, что на нее можно нажать.
Когда нам говорят, что где-то есть ручка — мы уже знаем, что за нее можно взяться.
И это весьма удобно.
Итоги
Действие — это последовательность других действий, задающих его алгоритм. Результат действия — какое-то изменение системы.
Сложность действия равна количеству элементарных действий его алгоритма для конкретного объекта.
Отношения между объектами и действиями определяет интерфейс объекта. Он хранит информацию о том, какие действия можно совершить с объектом.
Наш следующий вопрос:
Какова связь между действием и его исполнителем?
1.3 Объективный субъективизм
Наш следующий вопрос — как теперь считать сложность?
Вы можете резонно заметить:
“Но ведь если выполнять одни и те же действия, результаты могут быть разными! Если профессор физики может бегло прочесть статью по теории струн и все понять, то я при таком же подходе ничего не добьюсь. А чтобы получить похожий результат, мне придется искать определения через слово, читать другие статьи и потратить намного больше действий”.
Это хорошее замечание. У меня есть ответ на него.
Как и у любой задачи, у нашей есть начальные условия. Если вы их меняете — вы меняете саму задачу. И это приводит к тому, что для ее выполнения требуются разные действия.
Вы читаете статью. Предположим, что прочитав пару страниц, вы отложили ее. Теперь, для того чтобы статья была прочитана, вам нужно потратить меньше действий. Но изменилась ли от этого сложность самой статьи? Нет. Изменилось действие, которое вы будете с ней совершать. Было: “прочитать статью”, стало: “пролистать статью до момента, где я закончил, и дочитать до конца”.
Как нам тогда поступить с действиями? Мы зафиксируем желаемый результат. Как мы помним, к нему можно прийти разными путями.
Далее, мы можем разбить исполнителей на примерно одинаковые группы. Таких групп ограниченное количество, если у нас не бесконечное число исполнителей.
Теперь для каждой группы мы опишем действия которые приведут ее к желаемому результату.
Мы получили какой-то набор действий для каждой из групп исполнителей. Но что теперь делать со сложностью?
1.4 Вероятно просто
У нас есть набор действий. Каждое из них относится к определенной группе исполнителей. Мы знаем как посчитать сложность каждого из этих действий для каждого конкретного объекта.
А что, если мы попробуем задать вероятность попадания исполнителя в одну из групп?
Задача превращается в классическую задачу по теорверу.
У нас есть величины сложности действий. У нас есть вероятности выполнения каждого из действий случайным человеком.
Мы можем найти “среднее значение” нашей сложности. Это так называемое математическое ожидание(ru). Для этого, нам нужно каждую сложность действия с объектом умножить на вероятность его совершения.
Откуда взять эти вероятности и как разбить исполнителей на группы, если вы еще не знаете кто конкретно будет выполнять действия с объектом? Хороший вопрос!
Его рассмотрение выходит за рамки нашей статьи, но я приведу один интересный на мой взгляд пример.
Вы автор. И ваша задача — написать статью на сайт в котором есть тематические разделы. Когда вы выложите статью, она отобразится в общей ленте и ленте “своего” раздела. У разделов есть подписчики, они составляют какой-то процент от аудитории сайта. Общая лента показывается всем. Будем считать, что подписанные на раздел разбираются в его теме, а не подписанные — нет.
Пусть наша статья будет по физике. Мы проанализировали аудиторию и знаем, что на раздел «физика» подписано 3% аудитории сайта. Мы узнали, что вероятность того, что подписчик этого раздела зайдет в статью из него — 80%. Еще мы узнали, что вероятность посещения статьи из общей ленты 5%.
Кто наш потенциальный читатель и стоит ли нам “оптимизировать” статью под человека, который не подписан на раздел “физика”? Иными словами, какова вероятность того, что нашу статью читает человек, разбирающийся в физике?
Итак, внимание, данная вероятность равна… Примерно 33%.
Чуть больше, чем две трети наших потенциальных читателей не разбираются в физике, и нам стоит это учесть.
Как так получилось? Вкратце: высокая вероятность посещения статьи человеком, разбирающимся в физике, компенсируется их малым количеством. Небольшой шанс посещения статьи из общей ленты начинает играть существенную роль в нашей оценке. Хотите узнать об этом подробнее? Вот ссылка на неплохую статью о теореме Байеса(ru, en).
Если вы хотите проверить:
Вероятность того, что какой-то человек посетит статью = вероятность посещения из общей ленты плюс вероятность посещения статьи из раздела. В общей ленте так же находятся наши «оставшиеся» физики, не посетившие статью в разделе. Тогда мы получаем, что вероятность посещения статьи физиком из общей ленты = 0.05*0.03*0.2 = 0.0003, или 0.03%.
Всего из общей ленты было 5% посетителей, значит из них не физиков 4.97%
Теперь находим отношение физиков к общему числу посетителей. Для этого делим всех физиков (2.4% + 0.03%) на общее число посетителей.
(2.4+0.03)/(2.4+4.97+0.03) = 0.328.
Ответ: ~33%
Мы поговорили о действиях и тех, кто их исполняет. Время перейти к последнему вопросу.
Мы часто использовали слово объект, но оно не дает нам никакой информации о нем. Нужно какое-то описание, достаточно абстрактное, чтобы мы могли применять его для многих сущностей, и достаточно информативное, чтобы мы смогли с ним работать.
Как описать объекты, с которыми мы работаем?
1.5 Систематизация моделирования
Система — это совокупность компонент, которыми могут быть определенные заранее элементы и построенные с их помощью подсистемы.
Модель — это отображение системы, базирующееся на другом множестве элементов (терминов модели).
Я решил попробовать обобщенно описать тексты, таблицы, схемы… etc. Но как это сделать?
Давайте вернемся на шаг назад и посмотрим, как происходит их “создание”, возможно это поможет нам.
Мы пишем текст. У нас есть некая идея, мы формулируем ее в словах и записываем. При этом идея может быть не только в форме других слов. Мы можем описывать картину, музыку, математические объекты.
Я пишу код. У меня есть требования, которые я “перевожу” в код. Они могут быть выражены словесно или представлять собой изображение, например набросок интерфейса.
Мы составляем схему. У нас есть какие-то объекты, отношения между которыми мы описываем этой схемой.
Есть в этих процессах что-то общее. У нас есть какая-то система. Мы переводим ее в другую систему, при этом не обязательно использующую те же “термины”.
Мне кажется, что для описания этого процесса подходит слово “Моделирование”.
Итак, модель — это система, описывающая другую систему с использованием заданных обозначений (терминов).
Это определение подталкивает к резонному вопросу:
Что такое система?
Система — это совокупность каких-то компонентов. Она задается множеством их возможных состояний и текущим их состоянием. Компоненты системы я часто буду называть объектами.
Ими могут являться элементы (нечто, определенное заранее) и другие системы, состоящие из этих элементов. Есть еще такие штуки как связи — они появляются, когда мы хотим ограничить или определить возможные состояния одного объекта в зависимости от других.
Пример:
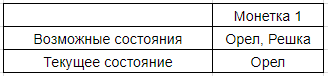
Есть система из 2-х монет. Одна из них в состоянии “орел”, другая в состоянии “решка”.
«Орел» и «решка» — это элементы нашей системы.
Монетка — это подсистема, которая состоит из элементов «орел» и «решка» и может находится в одном из этих состояний. Для первой монеты:
Предположим, что мы не можем перекидывать монетки и таким образом вносить изменения в систему. В этом случае наша система может быть описана как:

Если мы можем перекидывать монетки, то наша система описывается как:

Между некоторыми системами есть зависимости. Предположим, состояние второй монетки не может быть равно состоянию первой.
Тогда множество возможных состояний монетки 2, с учетом нашего ограничения — все предыдущие возможные состояния, кроме того в котором находится монетка 1.

В этом случае мы можем сказать что состояние монетки 2 определяет состояние монетки 1.
Теперь давайте посмотрим, что получится, если мы изменим множество возможных состояний монеток, добавив туда “ребро”.
Мы можем составить все пары для состояний монеток 1 и 2.

В этом случае мы говорим об ограничении возможных состояний монетки 2.
 — система.
— система.  — состояние системы.
— состояние системы.  — множество возможных состояний.
— множество возможных состояний. — текущее состояние.
— текущее состояние. Статический случай:

Если
 — элемент, то он остается как есть, т.к. по определению не разбивается.
— элемент, то он остается как есть, т.к. по определению не разбивается.Динамический случай:
 .
. Про связи.
Функция состояния некоторой системы от других систем может быть однозначной, и тогда мы говорим о том, что состояние определено состояниями других систем, или многозначной и тогда мы говорим об ограничении состояний системы.
Переводя в теорию множеств:
Есть некоторое множество систем 

Возьмем декартово произведение 

Положим 
Возьмем множество упорядоченных пар 
Если для одинаковых 


Если для одинаковых 

P.S.
Кстати, можно доказать, что имея всего лишь два элемента (0 и 1, например), вы можете описать любую систему, количество объектов которой — счетно. При условии, что вы можете неограниченно создавать последовательности элементов. На мой взгляд это интересный факт.
Я вдохновлялся статьями по теории систем(ru) и абстрактными автоматами(ru). Этот вариант математического описания понятия «система» чуть короче, чем найденные мною.
Вернемся к моделям
Моделью мы называем другую систему, которая является отображением первой. В общем случае она может быть построена из других элементов. Модель системы — карта, сама система — территория(en). Никто не мешает строить модели других моделей. Вы же можете нарисовать карту карты(en).
Давайте попробуем строить модели.
Начнем с классики: черный ящик.
У вас есть: “вход”, “выход” и ящик. Вы обозначаете компоненты, которые вы бы хотели менять, чтобы получить результат как “вход”, компоненты представляющие результат как “выход”, а остальную часть — как черный ящик. Такая модель не описывает внутренних зависимостей системы, а скрывает их. Мы не знаем как получается результат.
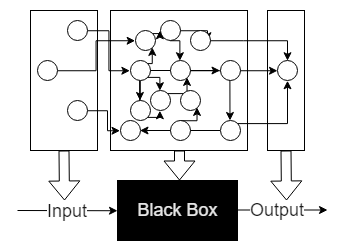
Такой подход часто используется в случаях, когда мы хотим изучить работу какой-то системы, но при этом не можем ее “вскрыть”. Например в психологии. Мы даем людям тестики, они решают их. Мы не знаем, что в этот момент происходит в голове у людей. Но, собрав достаточно данных, можно описать устройство ящика, которое будет давать похожие результаты. В части Machine Ex Homo мы посмотрим на это более подробно.
Теперь построим модель, отображающую все множество компонент и их возможных состояний.
Вы живете в Древней Греции. Ваш сосед Зенон(ru) уже достал вас. Этот Аидов сын каждый вечер вламывается к вам в дом с очередной мозговзрывающей загадкой(ru), а после этого вы проводите бессонную ночь в размышлениях. Вам надо поспать и для этого нужно заткнуть его хотя бы на пару дней.
Последний раз он прибегал с историей про Ахиллеса, бегущего за черепахой(ru). Во время этой ночи ваш взгляд упал на одно из ведер. В голову пришла интересная мысль: рассмотреть его апорию более предметно, используя ведерки и камни.
Вы хотите сделать так, чтобы у вас была возможность узнать положение Ахиллеса и черепахи относительно начальной точки, на каждый шаг черепахи. У нас есть: черепаха, которая шагает, Ахиллес, который в 10 раз быстрее черепахи. И их начальные положения: 1000 шагов и 0 шагов.
Наша модель пока не умеет представлять числа. И по ней совершенно невозможно различить, где Ахиллес, где черепаха, где путь.
С представлением натуральных чисел просто: возьмем ведро, положим количество камней, равное этому числу.
Теперь мы можем описать скорость и путь. В ведре, которое обозначает скорость Ахиллеса будет 10 камней. В ведре для скорости черепахи — один камень. Теперь перейдем к «ведрам пути». В черепашье положим тысячу камней, Ахиллесово оставим пустым. Когда черепаха будет делать шаг, переложим камни из скорости в путь. Готово?
Пока нет. У нас нет краски, чтобы подписать ведра. Только камни. Как справиться с этим?
Как вариант, мы можем поставить черепашье ведро «скорость» справа от ее «ведра пути». Проделать тоже самое с ведрами Ахиллеса. И отодвинуть ведра черепахи. Теперь мы знаем, что в комбинации «два ведра» — правое ведро скоростное, а левое — путевое.
Вы смотрите на две группы по два ведра. Для того, чтобы узнать какая из групп Ахиллесова — вам придется подойти, посмотреть в ведро, посчитать в нем камни, вспомнить, что скорость Ахиллеса 10 шагов, и сделать вывод о принадлежности ведер Ахиллесу. А если мы захотим внести какие-то изменения и сделать скорость Ахиллеса равной скорости черепахи? Тогда наш способ проверки на Ахиллесовость вообще перестанет работать!
Поэтому перед ведрами скорости и пути мы поставим «ведро имени». Теперь оно стало самым правым. И пусть наше правило выглядит так: если ведро имени — пустое, то следующие за ним ведра — черепашьи. А если там лежит камень, то эта группа ведер обозначает Ахиллеса.
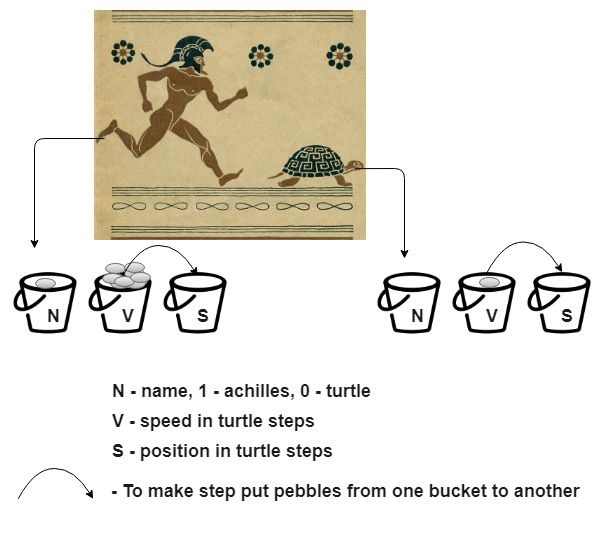
Я не рисовал камни в S, но думаю понятно, что для первого шага ахиллесово ведро пустое, а черепашье содержит 1000 камней.
Вы ликуете. Теперь Зенону придется изрядно подумать над тем, почему он решил, что сможет вечно продолжать процесс деления камней. По крайней мере вы на это очень надеетесь.
К сожалению, улучшить сон вам это не помогло. Зенон действительно не пришел на следующий вечер, но теперь вы сами глубоко задумались. Настанет ли тот момент, когда нельзя будет делить камни(ru)?
Смотрите, для каждого шага мы получили какое-то свое состояние каждого из рассматриваемых нами объектов. Положению Ахиллеса соответствует одно ведро, черепахи — другое. Для скоростей ситуация аналогична. Наша модель полностью описывает все возможные состояния всех объектов моделируемой системы.
Текст — это тоже модель системы. Терминами в этом случае являются слова. Они определены их смыслом, или множеством смыслов, которое ограничивается в зависимости от контекста.
Наши ощущения — это тоже модель, которую создает наш
Короче, с моделями вы сталкиваетесь постоянно.
Вы еще помните, зачем мы все это делали? На всякий случай: мы давали определение для модели, чтобы потом посчитать её сложность. Время пришло, давайте посмотрим, как можно это применять.
Вы — UX дизайнер. Ваша задача: сделать страницу настроек приложения. Вы знаете, что они не будут меняться в дальнейшем. Всего их десять штук: пять графических и пять настроек уведомлений.
Вы можете оставить их все на одном экране. У вас также появилась идея, что можно сделать на первом экране пункты «графика» и «уведомления», и переход на соответствующий экран с пятью настройками.
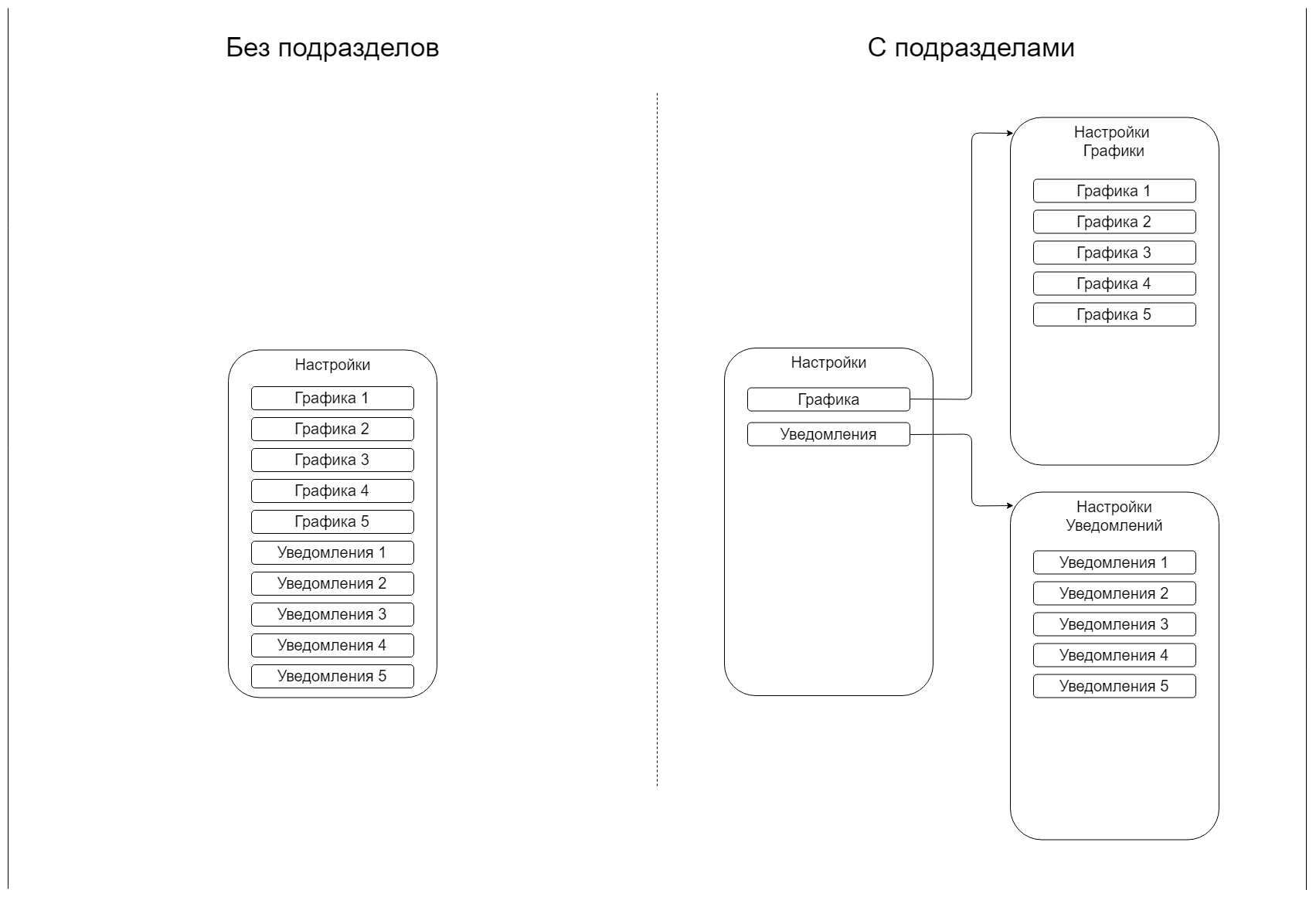
Давайте считать, что наш пользователь обладает очень плохой памятью и привычкой читать сверху вниз. Но при этом он все же достаточно умен, чтобы не ошибиться разделом, в случае когда мы сгруппировали опции. Названия экранов он не читает и переходит сразу к пунктам меню.
У нас всего 10 настроек, их можно отобразить на экране списком, и пользователь просто ткнет в нужный пункт. Мы считаем, что пользователю не нужно скроллить лист в этом случае. С другой стороны, если пользователю потребовались настройки из конца — ему будет проще найти их, ведь ему не придется читать весь список, он сможет пропустить половину ненужных ему пунктов.
Какая модель даст нам более простое взаимодействие?
Действия, которые может совершить пользователь c элементом списка: прочитать и ткнуть в него. Если переводить на язык интерфейсов: пункт меню обладает свойствами читабельности и тыкабельности. Все пункты у нас короткие, так что разницей в сложности их чтения — пренебрежем. Будем считать, что действия «ткнуть» и «прочесть» элементарны в нашем контексте. Их сложность 1.
Мы ожидаем, что пользователю с одинаковой вероятностью может потребоваться любой из пунктов. Выносить какие-то из них наверх смысла нет.
Разумеется, у вас уже есть какая-то догадка насчет ответа. Я предлагаю вам записать ее, а так же записать вашу уверенность, в том что ваш ответ правильный. Например, по шкале от 1 до 10, где 10 — абсолютно уверен, 1 — вообще не уверен. Вам потребуются эти данные для того, чтобы сравнить их с результатом. Под спойлером «Решение» будет находиться опрос. К сожалению, хабр не позволяет делать опросы в любом месте текста, так что ссылка ведет на гуглоформы. Там вы сможете пройти его и посмотреть статистику по общим результатам.
Я советую вам взять ручку, бумажку, открыть калькулятор и посчитать сложность самим. И только после этого открывать спойлер.
Прочитать первый пункт -> прочитать второй -> ткнуть пальцем, а сложность соответственно: 2+1 = 3.
Чтобы найти среднюю сложность нам потребуется найти сложность навигации до каждого из пунктов, сложить их и поделить на 10.
Для пунктов на одном экране: ((1+1)+(2+1)+(3+1)+(4+1)+(5+1)+(6+1)+(7+1)+(8+1)+(9+1)+(10+1))/10 = 6.5
Теперь перейдем к сложности варианта с разбиением на подменю. Для того, чтобы найти нужную опцию, сначала нам надо выбрать нужный раздел и ткнуть на него. Для первого пункта действия выглядят так:
Прочитать название первого раздела -> ткнуть -> прочитать название первого пункта -> ткнуть.
Сложность 4.
Давайте честно посчитаем:
((2+1+1)+(2+2+1)+(2+3+1)+(2+4+1)+(2+5+1)+(3+1+1)+(3+2+1)+(3+3+1)+(3+4+1)+(3+5+1))/10 = (4+5+6+7+8+5+6+7+8+9)/10 = 6.5
Они одинаковы?!
…
…
…
Честно говоря, когда я придумал этот пример, я ожидал другого ответа. Мне казалось, что способ с группировками в этой задаче лучше.
Как я и обещал, вы можете поучаствовать в опросе и посмотреть статистику по ответам. И пожалуйста, не пользуйтесь тем, что можете отправить несколько ответов. Я не хочу заставлять вас логиниться в гугл аккаунт, чтобы вам было удобнее отвечать и смотреть результат, а в обмен прошу не мешать собирать статистику.
Так, а если мы оставим пример таким же, но рассмотрим другое количество пунктов? 4 и 4, 3 и 3, 6 и 6?
Я снова предлагаю вам сделать все самостоятельно. Подсказка: прочитайте про сумму арифметической прогрессии и составьте уравнение, в зависимости от общего количества пунктов.
Ниже находится только ответ, так что, если вы хотите знать, как он получился, вам придется немного поработать.
При 6 и больше будет выигрывать вариант с разбиением.
При 4 и меньше будет выигрывать вариант с одним списком.
Этот пример я вставил в статью на этапе финальных правок. Мне было важно подытожить то, о чем мы говорили. Связать информацию из предыдущих глав в понятной форме. Так, чтобы вам было легко ее представить и попробовать использовать то, о чем мы говорили.
Я ошибся. Когда я писал этот пример, то думал, что знаю каким будет ответ. И сейчас я изрядно удивлен. Нет, это не правда. Когда я честно провел все вычисления, результат по мне очень сильно ударил. В моей голове происходило примерно следующее:
— *Хором* МЫ ОШИБЛИСЬ?!
— *Голос 2* Ну, да. И что с того?
— *Голос 1* Да я эти приложения днями и ночами вижу. Я кучу гайдлайнов прочитал. Я этих списков уже сотни сделал. У меня достаточно квалификации в моей области, чтобы поправлять ошибки наших же дизайнеров!
— *Голос 2* Ага, а дальше то что?
— *Голос 1* Я эту гребаную статью написал! Большая часть моей работы состоит в том, чтобы другим людям было проще взаимодействовать с моими решениями! Я занимаюсь этим годы! Не только в рабочее время, но и почти все свободное. Мой опыт давно перевалил за банальные 10к часов!
— *Голос 2* Парень, я вообще-то тоже ты. Ты не сказал ничего нового, перейди к сути.
— *Голос 1* Я делаю вывод, что мой пример синтетический. Он не отображает реальность, в ней все будет по другому, и поэтому ответ, который я предположил первым, будет правильным. Мой опыт позволил мне учесть намного больше, чем было в этом примере.
*Включаются сирены и красные лампы*
— *Голос из громкоговорителей* Говорит та часть твоего сознания, которою мы настроили для обнаружения ошибочных шаблонов в
— *Голос 1* Самообмана нет! Вы знаете, что все, что я сказал мы считаем правдой!
— *Голос 2* А ты знаешь, что есть большая разница между реальностью и твоим мнением насчет того, какая она должна быть.
— *Голос 1* Ну блииииииин, опять эти лекции.
— *Голос 2* Представь, что ты поверил в то, что люди умеют летать. Спасет ли тебя это при прыжке с крыши?
— *Голос 1* Не могу. Я же вижу, что другие люди не летают, значит не буду делать о себе такой идиотский вывод. И вообще, ты гиперболизируешь.
— *Голос 2* Ты сошел с ума. Или тебя накачали наркотиками. Или на тебя надели идеальный костюм виртуальной реальности, ты провел в ней 5 лет и все люди там летали, ты сам умел летать, твой
— *Голос 1* Ладно,
— *Голос 2* Окей, а теперь вернемся к разбору полетов. Хех, клевый каламбурчик. Ты придумал этот пример. Ты знал о его правилах. Ты знал, что ты сильно его упрощаешь, в сравнении с реальностью. Ты знал, как его решать. И ты ошибся в своем изначальном предположении.
— *Голос 1* Это не я! Я сделал выбор интуитивно, ты знаешь как это работает!
— *Голос 2* А ты знаешь, что это часто работает неправильно. И вот тебе еще одно доказательство.
— *Голос 1* А что с моим последним аргументом? Ведь это и правда приближение, и в реальности все будет по другому.
— *Голос 2* Этот аргумент — истинный. В реальности все будет по другому. Только из него не следует, что ты был прав.
Представь: ты начинаешь приближать пример к реальности. Ты честно считаешь отношения сложностей действий «ткнуть» и «прочитать», ты проводишь исследование, как люди смотрят на экран, какой части названия в этом списке им достаточно, чтобы понять, что это не тот пункт.
Ты дополняешь этот пример огромным количеством условий, он становится в сотни раз сложнее.
Прости, но в этом случае вероятность того, что ты получил правильный ответ «потому что интуиция» намного ниже, чем ~50% которые есть у случайного выбора.
Ты так уверен, что реальность встанет на твою сторону? Почему? Докажи.
— *Голос 1* Да не уверен я! Просто…
— *Голос 2* Сложно. Сложно признать, что ты ошибался, я знаю. Но ты понимаешь, почему нам это нужно. То, что эта ситуация произошла говорит лишь о том, что мы — тормоз и обучаемся медленнее, чем нам хотелось бы. Но мы знаем что надо делать.
— *Голос 1* Simple truth перечитать, что ли?
— *Голос 2* Очень хороший вариант. Нас это всегда успокаивает в таких ситуациях. Еще ты можешь глубоко подышать. И да, мы разобрались с этой ситуацией меньше чем за 1,5 минуты. Видал как быстро сработала система обнаружения ошибки? Мне кажется, мы заслужили пирожок. Его нет на полке, там гребаное Потенциальное Ведро, но мы его себе купим.
— *Голос 1* И все же интересно, что будет в реальности…
— *Голос 2* Ты что, забыл зачем мы пишем статью?!
…
…
…
Я извиняюсь за столь объемные отступление и пример. Возможно вы не готовы читать дальше, и вам хочется еще раз все обдумать. И это хороший выбор.
В начале есть оглавление, можете добавить статью в закладки и быстро вернуться к этому месту.
Вы все же решили продолжить? Тогда, у нас осталась последняя тема из тех, которые я хотел поднять.
1.6 Бегущий по лезвию
Бритва Оккама со стороны простоты системы.
Обозначим сложность изменения за 



Если 
Если 
Если 
Если предположить что сложность растет с количеством объектов в модели, и что у нас уже есть определенный набор моделей — мы получим, что наилучшим вариантом является модель с минимальным количеством объектов, что очень похоже на формулировку Бритвы Оккама.
Скорее всего вам известна Бритва Оккама, но я на всякий случай напомню:
“Не следует привлекать новые сущности без крайней на то необходимости”.
Вообще этот принцип интерпретируется так: из всех гипотез наиболее вероятна та, которая описывается самой короткой подпрограммой (или проще говоря — та, которая короче)(ru, en1, en2).
Как это выглядит в реальной жизни:
Если вы включили свет, и загорелась лампочка, то гипотезы могут быть такими:
- Выключатель замкнул электрическую цепь и ток пошел через лампочку.
- Выключатель пнул маленького гнома, который соединил провода, в результате чего цепь замкнулась и ток пошел через лампочку.
- Выключатель пнул маленького гнома, который толкнул вагонетку, в которой сидел маленький дракон, который испугавшись изверг пламя, которое расплавило припой, который соединил провода, в результате чего цепь замкнулась и ток пошел через лампочку.
Из этих гипотез предпочтительнее та, в которой содержится меньше сущностей, без гнома. Если же включая лампочку вы услышали тихую ругань из выключателя — предпочтительнее вторая гипотеза, потому что первая не объясняет, почему выключатель ругается, а последняя содержит избыточные сущности.
Буду честен. Когда я впервые услышал о Бритве Оккама, я не думал о гипотезах. А ее расплывчатая формулировка в словесном виде навела меня на мысль, что это общий принцип — уменьшай количество сущностей, которые есть в твоей системе и все будет круто.
Я сильно ошибался.
Но когда у меня появилось описание простоты системы, я понял как подправить мою неверную трактовку этого принципа. И сделать из нее нечто полезное.
У нас есть система До и После какого-то изменения.
Если разница сложностей До и После больше, чем сложность самого процесса внесения изменения — это изменение оправдано. Подразумевается, что изменение не повлияло на результат (по крайней мере на ту его часть, которая нам нужна). Назовем это… Необходимым условием упрощения.
Еще раз:
Ожидаемое упрощение системы после изменения должно быть больше, чем сложность самого изменения.
Если обозначить сложность изменения за 



Еще мы можем выразить некий аналог кпд для нашего изменения.

Если 
Если 
Если 
Зачем он нужен? Ну, например вы действуете в условиях, когда у вас ограничено время, и вы бы хотели расставить приоритеты изменениям которые вы хотите внести. Изменения с большим 
Пример:
У нас есть два текста, один с примером другой без.
С одной стороны — мы увеличили объем текста, тем самым усложнив его. Но с другой стороны, благодаря этому какая-то часть читателей не пойдет вбивать в гугл “пример бритвы оккама”, что является более сложным действием, чем просто чтение. Если по нашей оценке таких читателей будет много, то введение примера приведет к упрощению нашей статьи.
Нельзя забывать и про то, что для его описания мы тоже сделали какие-то действия, и у них была своя сложность. Если мы потратили слишком много действий, а упрощение было мало — введение нашей сущности “не окупается”.
Хм, а как связано это все с Бритвой Оккама?
Давайте предположим, что у нас уже есть несколько систем. И сложность их прямо зависит от количества сущностей (в реальном мире это не всегда правда, как мы уже выяснили). Результаты действий с этими системами нас устраивают.
Поскольку системы уже есть, то 


Что еще можно описать с помощью этого условия?
Например, можно оценить когда стоит применять различные практики улучшения кода, а когда это бессмысленно.
В самом деле, если вы пишете задачу в вузе, код которой прочтут один раз (или вообще не прочтут, а просто посмотрят как он работает), то вам не стоит париться над тем, чтобы он хорошо читался.
А вот если вы пишете для OpenSource проекта, и с вашим кодом будут работать сотни людей, или пишете свой проект, который планируете развивать, стоит озаботиться его качеством.
Если вы пишете конспект, вам стоит оценить, потребуется ли он вам в будущем. Если преподаватель будет проверять только его наличие, а всю информацию проще найти в гугле, то зачем усложнять?
Если вы пишете статью — определите как вы видите взаимодействие с ней. Например эта статья рассчитана не только на однократное прочтение. Я постарался оптимизировать ее для быстрого поиска. Именно поэтому под каждой частью есть спойлер «Кратко» и оглавление в начале.
Эх, если бы у нас был способ как-то описать, как человек будет читать нашу модель, и найти сложность этой модели для чтения. Мы бы могли точно сказать, как наши действия будут влиять на сложность этого процесса и применять нашу теорию в огромном количестве практических задач.
К сожалению, для этого нужно составить общий алгоритм чтения людьми любой модели. Если вам показалось, что это очень сложная задача — вы правы.
К счастью, часть этой работы я уже сделал.
В следующей главе, которая будет называться Machine Ex Homo мы будем разбирать, как наш
Короче — будет интересно, я обещаю.
Во первых, знайте — вы большой молодец. И я хочу сказать вам спасибо, потому что для меня важно, что вы ее прочитали.
И я хотел бы попросить о помощи.
Вернее не так: я потратил огромное количество времени, чтобы создать эту статью. Если она вам понравилась, вы сочли ее полезной или интересной, то мне кажется честным попросить у вас что-то взамен.
Нет, не деньги, все не настолько тривиально. Мне нужно ваше время.
Как я уже говорил, мне важно, чтобы мою статью читали. И мне важно качество моей статьи.
И, если вам не сложно, пробегитесь по публикации и сообщите об ошибках или идеях для ее упрощения. К сожалению, мое время ограничено, и я физически не могу сделать все идеально.
Если у вас появились другие идеи, как вы можете мне помочь, напишите их на почту simple.explanation.of.simple@gmail.com. То же самое вы можете сделать, если у вас просто появилось такое желание, но вы пока не придумали как. Расскажите о себе, и мы вместе подумаем, возможно найдется что-то, чем вам будет интересно заняться.
Лицензия:
CC BY-NC-SA 4.0
Автор: LonelyDeveloper97







