Cистема визуально-инерциальной навигации для дрона на C++

2026-02-06 в 14:16, admin, рубрики: c++, kalman filter, opencv, Raspberry Pi, SLAM, vio, visual odometry, дроны, навигация, робототехника

Дроны, которые работают на GPS, глушатся и это большая проблема для летательных аппаратов. Сигнал от спутников GPS проходит около 20 000 км и достигает антенны дрона с минимальной мощностью. Любая наземная глушилка, излучающая шум на частотах L1/L2/L5, для приемника дрона оказывается в тысячи раз громче спутников. Приемник слепнет, дрон теряет координаты, переходит в аварийный режим и сносится ветром.

И поэтому нам нужна MVIO (Monocular Visual Inertial Odometry).

Это технология, которая позволяет дрону понимать свое положение в пространстве, используя только одну камеру и IMU. В этой статье мы разберем реализацию такой системы на C++. Мы увидим, как объединить видеопоток и данные акселерометра в реальном времени, используя фильтр Калмана и библиотеку OpenCV.

Весь исходный код, конфиги и инструкции по сборке лежат в репозитории на GitHub.

Финальным результатом работы конвейера является стабильная реконструкция 3D-траектории полета в реальном времени, где высокочастотный дрейф инерциальных датчиков эффективно компенсируется визуальными ограничениями, обеспечивая гладкую оценку состояния системы.

Демонстрация работы MVIO: слева - видеопоток с отслеживаемыми характерными точками, справа - реконструкция 3D-траектории движения дрона и оценка текущей позы в реальном времени

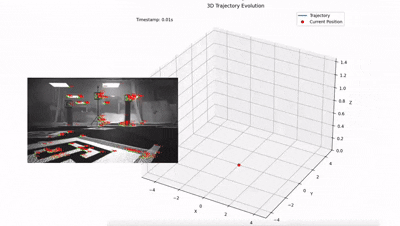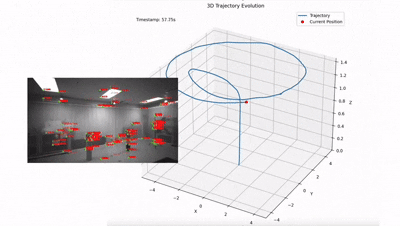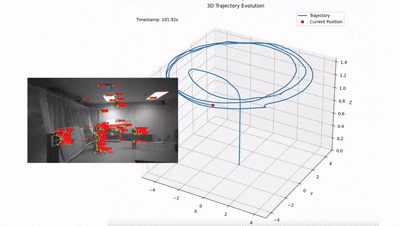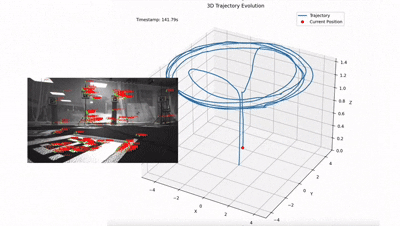
Монокулярное vs Стерео зрение

Стереокамера - это аналог человеческого зрения. У нас есть два глаза, разнесенных на фиксированное расстояние B. Если робот смотрит на объект двумя камерами одновременно, он видит его с небольшим смещением, диспаратностью d. Зная фокусное расстояние f и базу B, мы можем мгновенно вычислить глубину Z по школьной формуле триангуляции:

$Z=frac{f cdot B}{d}$

Однако, у нашего дрона камера одна. Закройте один глаз и попробуйте с ходу определить, насколько далеко от вас находится машина на парковке, это настоящий автомобиль в 50 метрах или игрушечная моделька в 50 сантиметрах? Геометрически на сетчатке они выглядят абсолютно одинаково. Это называется неопределенностью масштаба.

Чтобы понять глубину монокулярной камерой, дрон должен двигаться. Дрон делает кадр в точке A. Смещается в точку B. Делает кадр в точке B. По сути, мы создаем виртуальную стереопару, где базой служит расстояние, которое пролетел дрон между кадрами.

На схеме ниже показана траектория движения одной камеры в три последовательных момента времени $I_{k-1}, I_k, I_{k+1}$ .

Схема триангуляции в монокулярной одометрии: проекция 3D-точек мира на плоскости изображения движущейся камеры в последовательные моменты времени

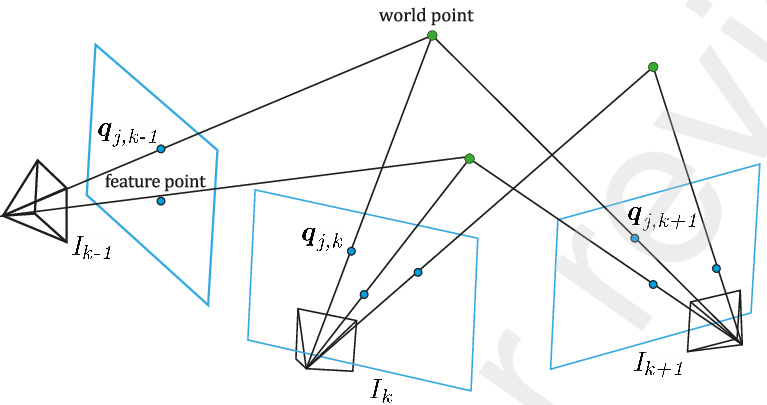
Зеленые точки - это реальные объекты в пространстве, которые остаются неподвижными. Синие точки на плоскостях - это их проекции на матрицу камеры, которые ползут по кадру по мере движения дрона.

Математика VIO занимается тем, что строит лучи от оптического центра камеры через пиксели на изображении. Точка пересечения этих лучей из разных кадров и дает нам координату объекта в 3D. Чем больше расстояние между кадрами, то есть база, тем точнее пересекаются лучи и тем надежнее мы вычисляем глубину.

Пиксельна GoPro с широким углом обзора и тот же пиксель на узкоугольной камере будут смотреть в совершенно разные точки пространства. Если мы ошибемся с направлением луча хотя бы на полградуса, на расстоянии в 10 метров наша зеленая точка уедет на метр в сторону, и карта рассыплется.

Чтобы превратить плоские координаты пикселейв реальные 3D-векторы направления, нам нужно математическое описание камеры дрона. В компьютерном зрении это называется Модель камеры-обскуры, а её цифровым воплощением служит матрица внутренних параметров K.

Давайте разберем её компоненты на примере нашего конфига camera.yaml

Фокусное расстояние - расстояние от линзы до матрицы сенсора

fx: 426.88
fy: 429.44

Если вы ошибетесь здесь, алгоритм будет неверно оценивать дистанцию. Если f завышено, алгоритму будет казаться, что объекты ближе, чем они есть, и он будет рассчитывать меньшую скорость полета дрона.

Оптический центр - точка на картинке, куда падает луч, идущий строго перпендикулярно центру линзы

cx: 424.99
cy: 245.67

Мы собираем эти параметры в одну структуру cv::Mat, которую OpenCV использует для всех расчетов

camera.cameraMatrix = (cv::Mat_<double>(3, 3) << 
    config.fx, 0.0,       config.cx,  
    0.0,       config.fy, config.cy,  
    0.0,       0.0,       1.0);

Без точной калибровки этих четырех цифр (fx, fy, cx, cy) любая навигация превратится в гадание. Матрица калибровки уникальна для каждой камеры, как отпечаток пальца, из-за микроскопических погрешностей сборки объектива. Вы не можете просто скопировать чужие настройки, для корректной работы навигации необходимо вручную откалибровать именно ваш сенсор.

Feature Detection и Feature Tracking

Обработка сырых данных сенсора, генерирующего поток порядка пикселей с частотой 30 Гц, накладывает жесткие ограничения на бюджет процессорного времени. В задачах визуальной одометрии это решается путем понижения размерности данных, перехода от анализа всего кадра к отслеживанию множества ключевых точек.

Ключевая точка - это точка с высоким локальным градиентом (углы, контрастные границы), которые можно устойчиво отслеживать. Низкотекстурированные участки (небо, однотонные стены) обладают низкой информационной энтропией и не создают необходимых геометрических ограничений для оценки движения.

Существуют классические алгоритмы вроде SIFT или SURF для детекции ключевых кадров, которые дают превосходное качество и устойчивы к любому вращению и масштабу. Но у них есть фатальный недостаток: они слишком тяжелые. Расчет SIFT на Raspberry Pi может занять 100-200 мс на кадр, что сразу убивает идею Real-Time навигации.

Поэтому в нашем проекте используется ORB - алгоритм, разработанный в лабораториях OpenCV как эффективная альтернатива тяжеловесам.

В основе ORB лежит FAST. Как следует из названия (Features from Accelerated Segment Test), он находит углы, сравнивая яркость пикселя с кругом из 16 соседей. Это происходит молниеносно, так как требует лишь простых сравнений светлее/темнее. Голый FAST теряется, если дрон наклоняется. ORB добавляет к нему вычисление ориентации, делая точки узнаваемыми даже при маневрах. Так же, в отличие от SIFT/SURF, которые долгое время были обременены патентами, ORB свободен и является частью стандартной поставки OpenCV.

Мы будем использовать ORB только для детекции, а не для трекинга. Трекинг осуществляется через оптический поток.

Как только ключевые точки найдены детектором ORB, стратегия меняется. Запускать детектор на каждом кадре и пытаться сопоставить новые точки со старыми по дескрипторам, то есть цифровым «отпечаткам» текстуры в виде бинарного кода, слишком вычислительно дорого или .

Вместо этого мы используем гипотезу когерентности движения, то есть кадры поступают с высокой частотой в 30 Гц, а значит, смещение точек между ними невелико, и их окрестность выглядит почти так же. Это позволяет применить методы оптического потока.

Для реализации этой идеи мы используем метод Лукаса-Канаде. Это классический алгоритм, который вычисляет смещение, предполагая, что вектор движения постоянен в небольшой окрестности точки. Это позволяет отслеживать перемещение признаков с субпиксельной точностью, избегая тяжелого перебора дескрипторов на каждом кадре

Взгляните на визуализацию работы алгоритма в реальном мире:

Визуализация оптического потока: цветные линии показывают траектории движения автомобилей, отслеживаемые алгоритмом Лукаса-Канаде

Здесь цветные линии представляют вектора скорости , которые вычисляет метод Лукаса-Канаде. Алгоритм цепится за контрастные элементы движущихся автомобилей и строит их трек во времени. Для нашего дрона ситуация зеркальная, так как мир статичен, а двигается сама камера, но математика смещения пикселей остается неизменной.

ESKF и IMU Преинтеграция

Визуальная одометрия (VO) дает нам траекторию без масштаба и облака точек, а IMU дает нам масштаб и гравитацию. Чтобы объединить их, мы используем Error-State Kalman Filter (ESKF).

Почему не обычный Kalman Filter?

Классический KF работает с линейными системами. Полет дрона глубоко нелинейный процесс, особенно когда речь заходит о вращениях.

В нашем фильтре мы отслеживаем 15 величин.

Где:

- Положение в мировых координатах
- Скорость
q - Ориентация, кватернион
- Смещение акселерометра
— Смещение гироскопа

Итого, размер ковариационной матрицы у нас , для кватерниона в ошибке мы используем 3 угла возмущения .

В коде инициализация матрицы выглядит так:

// P - матрица ковариации ошибок (15x15)
P.setZero();
P.block<3, 3>(0, 0) = Eigen::Matrix3d::Identity() * 1e-4;
// ...
P.block<3, 3>(9, 9) = Eigen::Matrix3d::Identity() * 1e-2;

Между двумя кадрами камеры IMU успевает выдать 6-10 измерений. Если мы будем запускать шаг предсказания фильтра на каждое сообщение IMU, это сильно нагрузит систему. К тому же, для инициализации нам нужно знать, как сместился дрон между ключевыми кадрами, не зная еще точной ориентации.

Здесь помогает техника IMU Preintegration.

Мы интегрируем показания акселерометра и гироскопа в локальной системе координат, связанной с предыдущим кадром . Эти преинтегрированные дельты зависят только от IMU и не зависят от глобального положения дрона.

Математически шаг пропогации для одного измерения IMU выглядит так:

$Delta p_{k+1}=Delta p_k + Delta v_k Delta t + frac{1}{2} R_k (a_t - b_a) Delta t^2$

$Delta v_{k+1}=Delta v_k + R_k (a_t - b_a) Delta t$

$Delta R_{k+1}=Delta R_k cdot Exp((omega_t - b_g) Delta t)$

В коде это реализовано в методе propagate:

void ImuPreintegrator::propagate(const std::vector<ImuData>& imuBuffer) {
    for (const auto& imu : imuBuffer){ 
        // ... расчет dt ...
        
        Eigen::Vector3d acc_corrected = acc_raw - bias_a;
        Eigen::Vector3d gyro_corrected = gyro_raw - bias_g;

        // Интегрируем позицию и скорость
        delta_p = delta_p + delta_v * dt + 0.5 * delta_R * acc_corrected * dt * dt;
        delta_v = delta_v + delta_R * acc_corrected * dt;

        // Интегрируем поворот (на многообразии SO3)
        delta_R = delta_R * dR_step;
    }
}

Эти накопленные дельты мы используем на этапе инициализации VIO, чтобы решить систему линейных уравнений и найти вектор гравитации и масштаб сцены .

В основном цикле фильтра мы используем данные IMU для предсказания следующего состояния. Самое важное здесь - это пропогация ковариации.

Уравнение обновления ковариации:

$P_{k+1}=F P_k F^T + Q$

Где - якобиан системы, а- матрица шума IMU. Чем больше шум акселерометра, тем быстрее растет пузырь неопределенности между кадрами.

Когда приходит новый кадр с камеры и мы успешно триангулировали точки или решили PnP, мы получаем измеренное положение дрона $p_{meas}$ и ориентацию $q_{meas}$ .

Фильтр сравнивает своё предсказание, основанное на IMU, с измерением камеры. Разница между ними это innovation.

Магия ESKF в том, что мы корректируем не только позицию, но и скрытые параметры смещения акселерометра и гироскопа.

void KalmanFilter::update_pose(...) {
    // Вычисляем невязку
    Eigen::Vector3d r_p = p_meas - p;
    // ...
    
    // Вычисляем усиление Калмана (Kalman Gain)
    Eigen::Matrix<double, 15, 6> K = P * H.transpose() * S.inverse();

    // Получаем вектор ошибки dx (размер 15)
    Eigen::Matrix<double, 15, 1> dx = K * r;

    // Внедряем ошибку в номинальное состояние (Injection)
    p += dx.segment<3>(0);
    v += dx.segment<3>(3);
    
    // Корректируем кватернион на малый угол
    // ...
    
    // Обновляем biases
    ba += dx.segment<3>(9);
    bg += dx.segment<3>(12);
}

Именно благодаря строкам ba += ... и bg += ... система самообучается. Через несколько секунд полета дрон «понимает», что его гироскоп немного врет, запоминает эту поправку и начинает летать намного точнее, даже если камера временно потеряет картинку.

Алгоритм

Теперь посмотрим на алгоритм после того как мы рассмотрели все компоненты по отдельности. Архитектуру нашей системы можно разделить на визуальный фронтенд, отвечающий за обработку изображений, и инерциальный бэкенд, выполняющий слияние данных. Входной точкой системы служит метод обновления, который принимает очередной кадр и пакет данных акселерометра.

Первым этапом всегда идет обработка инерциальных данных. В зависимости от того, инициализирован ли уже фильтр, мы либо выполняем шаг п��едсказания состояния ESKF, либо просто накапливаем преинтегрированные измерения в буфере для последующей инициализации.

if (isInitialized) {
  estimator->predict(imuBuffer);
} else {
  imu.propagate(imuBuffer);
}

Следом запускается модуль оптического потока, который мы обсуждали ранее. Нам важно не просто найти точки, а понять, насколько значимо сместился дрон. Для этого вычисляется средний параллакс всех видимых признаков. Если смещение меньше заданного порога, кадр считается неинформативным и отбрасывается, чтобы не засорять карту точками с плохой триангуляцией.

std::vector<cv::Point2f> projectedPoints = track(nextFrame);
// ...
float avgDisplacement = getAverageParallax(projectedPoints);

if (avgDisplacement > config.averageThreshold) {
   // Дальнейшая обработка ключевого кадра
}

Когда смещение достаточно велико, логика ветвится. Если в поле зрения камеры находится мало точек с известной глубиной, что характерно для начала работы или потери трека, система переходит в режим инициализации карты. Здесь вычисляется фундаментальная матрица и производится триангуляция новых трехмерных точек из двумерных соответствий.

if (count3D < config.min3DPoints) {
    // ...
    if (!computeEssentialMatrixAndPose(currentPoints, projectedPoints, E, R, t, mask)) {
        return;
    }
    // ...
    triangulateInitialFeatures(R, t, inlierOriginalPoints, ...);
}

В штатном режиме, когда карта уже насыщена ориентирами, положение камеры определяется через решение задачи Perspective-n-Point. Это позволяет жестко привязать текущий кадр к глобальной структуре и получить точную оценку позы, которая затем будет использована как измерение для фильтра Калмана.

if (!estimatePosePnP(projectedPoints, R_wc, t_wc, inlierIndices, pnpIndices)) {
    updateFrame(nextFrame, projectedPoints);
    return;
}

Ключевым моментом, связывающим фронтенд и бэкенд, является процедура выравнивания визуальной и инерциальной траекторий. Пока система не инициализирована, мы накапливаем историю движений в буфере. Как только данных достаточно, запускается решатель, который формирует переопределенную систему линейных уравнений. Матрица системы заполняется блоками, связывающими кинематические параметры движения, а вектор правой части содержит данные преинтеграции IMU.

Eigen::MatrixXd A = Eigen::MatrixXd::Zero(dim_eq, dim_x);
Eigen::VectorXd b = Eigen::VectorXd::Zero(dim_eq);

for (int k = 0; k < N; ++k) {
    // ... заполнение блоков матрицы для скоростей и гравитации ...
    A.block<3, 3>(row2, idx_g) = -0.5 * dt * dt * Eigen::Matrix3d::Identity();
    A.block<3, 1>(row2, idx_s) = (P_k1 - P_k); // Связь масштаба s с перемещением
    // ...
}

Eigen::VectorXd x = A.colPivHouseholderQr().solve(b);

Решение этой системы методом QR-разложения дает нам физический масштаб сцены и вектор гравитации. Полученные значения проходят строгую валидацию: масштаб должен быть положительным и лежать в разумных пределах, а норма вектора гравитации обязана быть близкой к земному ускорению 9.81 метра на секунду в квадрате.

Eigen::Vector3d g_est = x.segment<3>(3 * (N + 1));
double s_est = x(3 * (N + 1) + 3);

if (s_est > config.vioScaleMin && s_est < config.vioScaleMax &&
    g_est.norm() > config.vioGravityMin &&
    g_est.norm() < config.vioGravityMax) {
    this->scale = s_est;
    this->estimatedGravity = g_est;
    // ...
}

После успешной валидации создается и инициализируется объект фильтра Калмана. С этого момента система переходит в рабочий режим. Каждое успешное визуальное измерение, полученное через PnP или триангуляцию, преобразуется в глобальную систему координат и подается на вход корректора фильтра, подавляя дрейф акселерометров и гироскопов.

if (isInitialized) {
    // ... преобразование координат из камеры в IMU ...
    estimator->update_pose(t_wb, q_meas, R_cov);
    
    // Получение отфильтрованного состояния для траектории
    Eigen::Vector3d t_filt_body = estimator->getPosition();
}