Статья посвящена описанию метода CRF (Conditional Random Fields), являющимся разновидностью метода Марковских случайных полей (Markov random field). Данный метод нашел широкое применение в различных областях ИИ, в частности, его успешно используют в задачах распознавания речи и образов, обработки текстовой информации, а также и в других предметных областях: биоинформатики, компьютерной графики и пр.
Краткое описание метода
(кто не любит математики и боится формул, можно сразу перейти на «сравнение методов»).
Марковским случайным полем или Марковской сетью (не путать с Маковскими цепями) называют графовую модель, которая используется для представления совместных распределений набора нескольких случайных переменных. Формально Марковское случайное поле состоит из следующих компонентов:
- неориентированный граф или фактор-граф G = (V, E), где каждая вершина
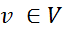является случайной переменной Х и каждое ребро 
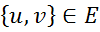представляет собой зависимость между случайными величинами u и v. - набор потенциальных функций (potential function) или факторов
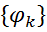, одна для каждой клики (клика — полный подграф G неориентированного графа) в графе. Функция 
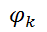ставит каждому возможному состоянию элементов клики в соответствие некоторое неотрицательное вещественнозначное число.
Вершины, не являющиеся смежными, должны соответствовать условно независимым случайным величинам. Группа смежных вершин образует клику, набор состояний вершин является аргументом соответствующей потенциальной функции.
Совместное распределение набора случайных величин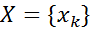 
в Марковском случайном поле вычисляется по формуле:
(1) 
,
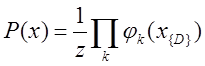где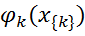 
– потенциальная функция, описывающая состояние случайных величин в k-ой клике; Z – коэффициент нормализации вычисляется по формуле:
(2) 
.
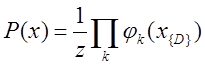Множество входных лексем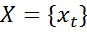 
и множество соответствующих им типов 
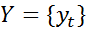в совокупности образуют множество случайных переменных 
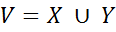. Для решения задачи извлечения информации из текста достаточно определить условную вероятность P(Y | X). Потенциальная функция имеет вид:
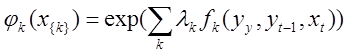, где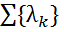 
вещественнозначный параметрический вектор, и
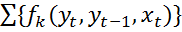— набор признаковых функций. Тогда линейным условным случайным полем называется распределение вероятности вида:
.
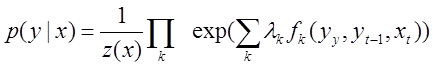Коэффициент нормализации тогда Z(x) вычисляется по формуле:
.
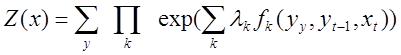Сравнение методов
Метод CRF, как и метод MEMM (Maximum Entropy Markov Models), относится к дискриминативным вероятностным методам, в отличие от генеративных методов, таких как HMM (Hidden Markov Models) или метод «Наивного Баеса» (Naïve Bayes).
По аналогии с MEMM, выбор факторов-признаков для задания вероятности перехода между состояниями при наличии наблюдаемого значения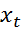 
зависит от специфики конкретных данных, но в отличие от того же МЕММ,
CRF может учитывать любые особенности и взаимозависимости в исходных данных. Вектор признаков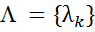 
рассчитывается на основе обучающей выборки и определяет вес каждой потенциальной функции. Для обучения и применения модели используются алгоритмы, аналогичные алгоритмам HMM: Витерби и его разновидность – алгоритм «вперед-назад» (forward-backward).
Скрытую Марковскую модель можно рассматривать как частный случай линейного условного случайного поля (CRF). В свою очередь, условное случайное поле можно рассматривать как разновидность Марковского случайного поля (см. рис).
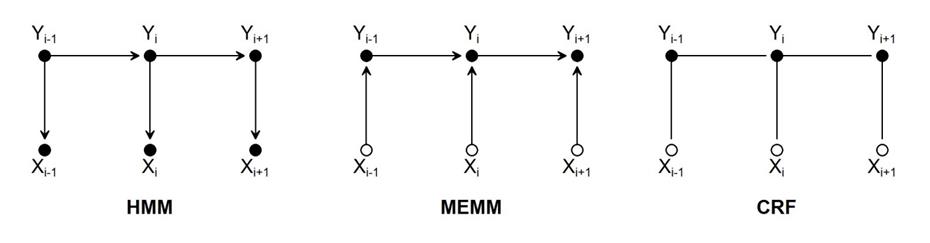
Рис. Изображение в виде графов для методов HMM, MEMM и CRF. Незакрашенные окружности обозначают, что распределение случайной величины не учитывается в модели. Стрелки указывают на зависимые узлы.
В условных случайных полях отсутствует т.н. label bias problem – ситуация, когда преимущество получают состояния с меньшим количеством переходов, так как строится единое распределение вероятностей и нормализация (коэффициент Z(x) из формулы (5)) производится в целом, а не в рамках отдельного состояния. Это, безусловно, является преимуществом метода: алгоритм не требует предположения независимости наблюдаемых переменных. Кроме того, использование произвольных факторов позволяет описать различные признаки определяемых объектов, что снижает требования к полноте и объему обучающей выборки. В зависимости от решаемой задачи, на практике достаточно объема от нескольких сотен тысяч до миллионов термов. При этом точность будет определяться не только объемом выборки, но и выбранными факторами.
Недостатком подхода CRF является вычислительная сложность анализа обучающей выборки, что затрудняет постоянное обновление модели при поступлении новых обучающих данных.
Сравнение метода CRF с некоторыми другими методами, используемыми в компьютерной лингвистике можно найти в работе [3]. В работе показано, что предлагаемый метод работает лучше остальных (по мере F1) при решении различных лингвистических задач. Например, в задачах автоматического нахождения в тексте именованных сущностей CRF демонстрирует несколько меньшую точность по сравнению с методом MEMM, но при этом значительно выигрывает в полноте.
Следует добавить, что реализация алгоритма CRF имеет хорошую скорость, что очень важно при обработке больших объемов информации.
На сегодняшний день именно метод CRF является наиболее популярным и точным способом извлечения объектов из текста. Например, он был реализован в проекте Стэндфордского университета Stanford Named Entity Recognizer. Так же этот метод успешно реализован для разных видов лингвистической обработки текста.
Список литературы
- Lafferty J., McCallum A., Pereira F. “Conditional Random Fields: Probabilistic Models for Segmenting and Labeling Sequence Data”. Proceedings of the 18th International Conference on Machine Learning. 282-289. 2001.
- Klinger R., Tomanek K.: Classical Probabilistic Models and Conditional Random Fields. Algorithm Engineering Report TR07-2-013. of Computer Science. Dortmund University of Technology. December 2007. ISSN 1864-4503.
- Антонова А.Ю., Соловьев А.Н. Метод условных случайных полей в задачах обработки русскоязычных текстов. «Информационные технологии и системы — 2013», Калининград, 2013.
http://itas2013.iitp.ru/pdf/1569759547.pdf - Stanford Named Entity Recognizer // http://www-nlp.stanford.edu/software/CRF-NER.shtml
Автор: elingur
