Многие алгоритмы являются детерминированными – то есть последовательность их действий зависит лишь от входных данных и программы. Но что будет, если разрешить алгоритму по ходу работы использовать случайные числа?
Оказывается, тогда становятся возможны интересные результаты, которых нельзя достигнуть с помощью обычных алгоритмов. Например, можно построить хеш-функцию, для которой противник не сможет легко подобрать коллизии. Или обработать большое множество чисел и сжать его во много раз, сохранив возможность проверять принадлежность чисел исходному множеству. Можно приближенно подсчитать количество различных элементов в потоке данных, располагая лишь небольшим объёмом дополнительной памяти. В этой лекции Максим Бабенко рассказывает школьникам, как именно это происходит.
Хэш-функции
Предположим, что мы хотим придумать структуру данных, которая в computer science называется ассоциативной таблицей. В этой таблице в два столбца записаны пары компонентов. Первый столбец называется «ключ», а второй – «значение». Ключом, например, может быть имя человека, а значением – его адрес. Наша задача – быстро выполнять поиск по этой таблице: находить строчку в таблице, где присутствует определенный ключ, и отдавать соответствующее ему значение. Вариант просмотреть всю таблицу сверху донизу нас не устраивает, так как мы хотим искать быстро. Если количество строк в таблице принять за n, то время поиска должно быть существенно меньше n. Мы считаем, что в нашей таблице все ключи уникальны. Если бы ключи были целыми числами, то все было бы достаточно просто. Нужно было бы создать массив, в котором элементы будут индексироваться возможными значениями ключа в диапазоне от нуля до m – 1, где m не слишком велико. Это подход хорош тем, что при таком способе хранения данных, для того чтобы по ключу k обратиться к соответствующей строке и найти соответствующее значение, нужно затратить константное время O(1). Недостаток этого способа заключается в том, что если вместо чисел в качестве ключей будут использоваться, например, строки, то придется кодировать эти строки числами. А при таком кодировании численный диапазон будет слишком велик.
И тут нам на помощь приходит хэширование. Допустим, у нас по-прежнему есть таблица размером m, но на этот раз m никак не будет связано с тем, какие у нас есть ключи. Ключи у нас – это некие целые числа. Как нам при таких условиях найти в таблице положение ключа k? Предположим, что мы знаем некоторую функцию – h(k), называемую хэш-функцией. Она для заданного k нам говорит, в какой ячейке из m возможных содержится этот ключ. Если не рассматривать, как именно работает хэш-функция, то все выглядит очень просто. Но тут есть подвох. Во-первых, у нас бесконечно много возможных значений ключей, а хэш-функция отображает на конечное множество. Поэтому, конечно же, когда два разных ключа после применения хэш-функции попадают в одну и ту же клетку: непонятно, как мы можем хранить их одновременно. Подобные ситуации называются коллизиями, и с ними нужно уметь бороться. Способов борьбы существует достаточно много. Один из простейших, но при этом довольно эффективный способ заключается в том, чтобы считать, что в ячейках содержатся не значения, и даже на пары ключ – значение, а целый список пар. Это все те пары, в которых ключи под действием хэш-функции приняли некоторое конкретное значение. Называется это разрешением коллизий методом цепочек.
Ключевой момент здесь – это выбор хэш-функции. Именно это влияет на эффективность. Если мы выберем h(k) = 0, то все хэши у нас будут равны нулю, и в итоге мы получим одну цепочку, в которой мы будем все время искать. Это очень медленно и невыгодно. Но если значения хэш-функции будут в какой-то мере случайны, то такого происходить не будет.
Случайность
Рассмотрим понятие случайности с точки зрения математики, а точнее, дискретный вариант этого понятия. Предположим, у нас есть обычный шестигранный кубик. Бросая его, мы генерируем некоторую случайность. Т.е. у нас есть множество элементарных событий – Ω. В нашем случае элементарным событием будет та грань, которая окажется сверху после полной остановки кубика. Обозначим грани (a, b, c, d, e, f). Далее нам нужно задать распределение вероятностей: создать функцию, которая для каждого элементарного события будет говорить, какова его вероятность от нуля до единицы. Т.к. кубик у нас ровный и шестигранный, то вероятность выпадения каждой стороны должна равняться 1/6.
Случайная величина в нашем случае – это любая функция, определенная на элементарных событиях. Если мы пронумеруем грани кубика числами от 1 до 6, то число, соответствующее выпавшей грани и будет случайной величиной.
Теперь рассмотрим понятие среднего случайной величины. Если элементарными событиями у нас являются сущности (a1, …, an), а вероятности им приписанные – (p1, …, pn), и наша функция отображает элементарные события на значения (x1, …, xn), то средним мы называем взвешенную сумму вида x1p1 + x2p2 + … xnpn. Т.е. нужно посмотреть, какие значения, и с какими вероятностями принимаются, после чего усреднить с коэффициентом, который равен вероятности наступления того или иного элементарного события.
Неравенство Маркова
Неформальный смысл этой леммы таков: если у случайной величины не очень большое среднее, то она не может часто принимать большие значения. Рассмотрим формальную постановку задачи и доказательство. Пусть будет задано дискретное вероятностное пространство (Ω, p) и случайная величина на нем – f * Ω → R1. Мы интересуемся вероятностью такого происшествия, что случайная величина приняла значение большее или равное ε, где ε – это некоторое положительное число.
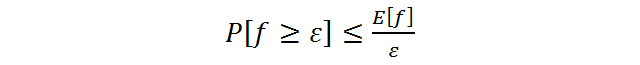
Перейдем к доказательству. Доказываемое неравенство можно переписать иначе:
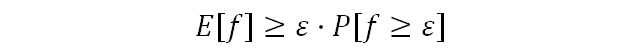
Вспомним, что E[f]=x1p1 + x22 + ⋯ + xnpn. Из этого мы можем сделать следующий вывод:
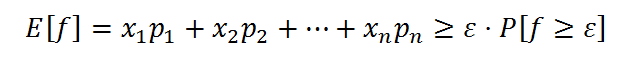
Посмотрев лекцию до конца, вы также узнаете, как приведенные выше построения помогают строить хэш-функции с низкой вероятностью коллизий, и выполнять другие алгоритмические задачи, которые без применения случайных чисел были бы невыполнимы или решались менее эффективно.
Автор: elcoyot