Данная статья скорее логическое продолжение моей статьи о балансере: «Создание робота балансера на arduino».
В ней будут очень кратко освещены: простая модель угловой стабилизации квадрокоптера с использованием кватернионов, линеаризация, построение управления для объекта и проверка его в Matlab, а так же проверка на реальном объекте. В качестве подопытного будет выступать Crazyflie 1.0.
Сейчас оно летает так (на момент съемок я не очень правильно выставил управление):
Построение динамической системы
Введем 2 системы координат: локальную, привязанную к земле, и вторую, связанную с коптером.

Вращение тела удобнее представлять, используя кватернионы, в связи с меньшим количеством необходимых вычислений. О них написано много статей, в том числе и на хабре. Я рекомендую к прочтению книгу «Бранец В.Н., Шмыглевский И.П. Применение кватернионов в задачах ориентации», спасибо Slovak из центра компетенций Matlab за подсказку.
Воспользуемся основным законом динамики вращательного движения:
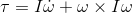 , где
, где
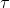 — моменты, действующие на тело,
— моменты, действующие на тело,
I — тензор инерции, а
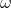 — угловые скорости по главным осям(в связанной системе координат).
— угловые скорости по главным осям(в связанной системе координат).
Таким образом:
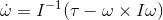 .
.
В силу теоремы о приведении тензора инерции к главным осям, тензор инерции представим в виде: 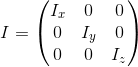 .
.
Внешние моменты определим через управления: 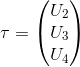 , где
, где
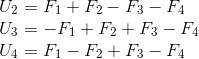
Таким образом, уравнения угловых скоростей в связанной системе координат:
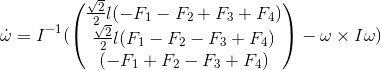
Замечу, что если бы мы учитывали положение коптера, можно было бы не вводить отдельные функции управлений, а сразу использовать в качестве них силы тяги, что удобнее и быстрее при расчетах. В данном случае система стабилизации не имеет никаких данных о необходимой сумме сил тяги, поэтому необходимо использовать именно такие управления…
Сила тяги пропеллера может быть примерно описана как 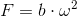 . Тогда уравнения можно записать через угловые частоты пропеллеров, если вы сможете управлять напрямую частотой моторов и знаете конкретное b:
. Тогда уравнения можно записать через угловые частоты пропеллеров, если вы сможете управлять напрямую частотой моторов и знаете конкретное b:
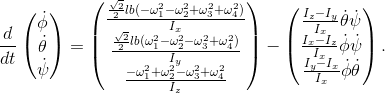 где
где
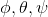 — углы эйлера
— углы эйлера
Замечу, что подбор коэффициента b у меня произведен вручную, простым подбором.
Также необходимо выписать уравнение для кватерниона вращения. Из свойств кватернионов следует, что
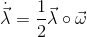 , где
, где 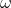 являются угловыми скоростями в связанной с ЛА системе координат, в ней гироскопы измеряют угловую скорость [1].
являются угловыми скоростями в связанной с ЛА системе координат, в ней гироскопы измеряют угловую скорость [1].
Попробуем стабилизировать только углы и угловые скорости:
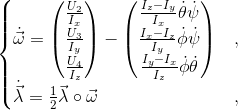
Или подробнее
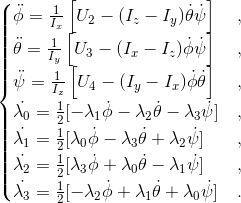
Введем вектор пространства состояний:
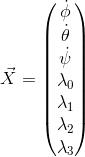 .
.
Необходимо заметить, что если в вектор пространства входит компонента 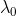 система перестает быть управляемой. Однако мы можем считать, что
система перестает быть управляемой. Однако мы можем считать, что 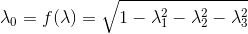 и убрать ее из вектора состояний, тем самым уменьшив количество координат [2].
и убрать ее из вектора состояний, тем самым уменьшив количество координат [2].
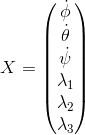
Вектор управлений:
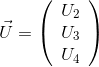 ,
,
Система представима в стандартном виде
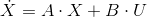 .
.
В нашем случае
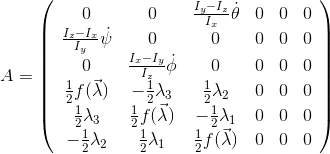 , а
, а
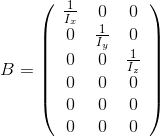
Линеаризация и построение управления
Линеаризируя систему вблизи начала координат получим следующие матрицы A и B:
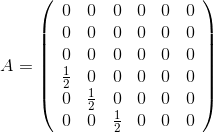 ,
,
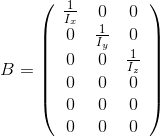
Как и в прошлый раз используем линейно-квадратичный регулятор. Напомню команду Matlab для его расчета:
[K,S,e]=lqr(A,B,Q,R)
Матрицы Q и R являются весовыми матрицами. Q штрафует за отклонение от нуля, а R за расход энергии управлением.
В результате получили матрицу K. В моей матрице коэффициентов все недиагональные элементы были очень малы (порядка 10^-4) и я не стал учитывать их.
Напомню, что для получения управления необходимо умножить матрицу K на вектор X. Конечно, в коде можно не вводить понятие матрицы и просто умножить каждую координату на некоторый коэффициент для быстродействия.
Проверка модели
Для проверки полученных результатов была создана модель в Matlab. Запустим ее с ненулевыми начальными условиями.
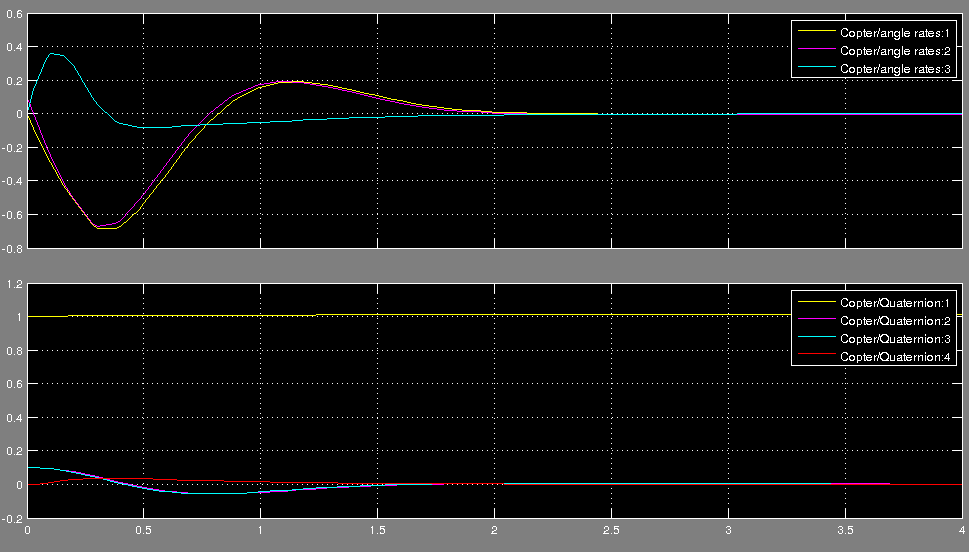
Первый график показывает как ведут себя угловые скорости, второй — изменение составляющих кватерниона. Заметьте, что скалярная величина кватерниона приходит в единицу, не смотря на то, что она не входит в уравнения линеаризованной системы. Как видно из графиков — модель стабилизируется.
Код
Crazyflie использует систему Free RTOS, где весь код разбит на модули, нас интересует код sensfusion6.c и stabilizer.c.
К счастью, фильтрация показаний акселерометра и гироскопа производится в кватернионах, проблема заключается в том, что сенсоры на коптере расположены для + схемы. Модель же я рассчитывал для X схемы. Отличие заключается только в выборе управлений U1 и U2.
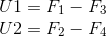
Необходимо добавить код получения кватерниона в sensfusion6.c:
void sensfusion6GetQuaternion(float* rq0,float* rq1,float* rq2,float* rq3){
*rq0=q0;
*rq1=q1;
*rq2=q2;
*rq3=q3;
}
Я не стал добавлять отдельный модуль для LQR регулятора, вместо этого я изменил stabilizer.c. Да, возможно, это и не самый интеллигентный способ, однако для проверки модели он подойдет.
Начать стоит с добавления переменных текущего и желаемого положения аппарата, а так же управлений:
static float q0Actual;
static float q1Actual;
static float q2Actual;
static float q3Actual;
static float q1Desired;
static float q2Desired;
static float q3Desired;
int16_t actuatorU1;
int16_t actuatorU2;
int16_t actuatorU3;
Желаемое положение по q0 не указываем в силу того, что нам не нужно его стабилизировать.
Произведем изменения в код получения команд. Коптер получает угол в градусах, математически правильнее сделать так:
сommanderGetRPY(&q1Desired, &q2Desired, &q3Desired);
q1Desired=cos((q1Desired/2+90)*0.01745);//*3.14/180/2;
q2Desired=cos((q2Desired/2+90)*0.01745);
q3Desired=cos((q3Desired/2+90)*0.01745);
Изменим «быстрый» цикл (250Гц) стабилизатора:
sensfusion6UpdateQ(gyro.x, gyro.y, gyro.z, acc.x, acc.y, acc.z, FUSION_UPDATE_DT);
sensfusion6GetEulerRPY(&eulerRollActual, &eulerPitchActual, &eulerYawActual);
sensfusion6GetQuaternion(&q0Actual, &q1Actual,&q2Actual,&q3Actual);
sensfusion6UpdateP(FUSION_UPDATE_DT);
sensfusion6UpdateV(acc.x, acc.y, acc.z, FUSION_UPDATE_DT);
actuatorU1=50*(1*(-gyro.x)+245*(q1Actual-q1Desired));
actuatorU2=50*(1*(gyro.y)-200*(q2Actual-q2Desired));
actuatorU3=50*(1.5*(gyro.z)+0*(q3Actual-q3Desired));
Подбор коэффициентов произведен опытным путем, так как не было возможности узнать зависимость между посылаемой на моторы командой и силой, которую выдает мотоустановка.
Также я изменил функцию распределения мощностей моторов:
static void distributePower(const uint16_t thrust, const int16_t u2, const int16_t u3, const int16_t u4)
{
motorPowerM1=limitThrust((thrust/4+u3/2+u4/4)*5);
motorPowerM2=limitThrust((thrust/4-u2/2-u4/4)*5);
motorPowerM3=limitThrust((thrust/4-u3/2+u4/4)*5);
motorPowerM4=limitThrust((thrust/4+u2/2-u4/4)*5);
motorsSetRatio(MOTOR_M1, motorPowerM1);
motorsSetRatio(MOTOR_M2, motorPowerM2);
motorsSetRatio(MOTOR_M3, motorPowerM3);
motorsSetRatio(MOTOR_M4, motorPowerM4);
}
Заключение
Исходя из того, что коптер стабилизирует свои углы, можно заключить, что математическая модель разработана верно. К сожалению, пока нет возможности получать свои координаты и скорости (интегрирование акселерометра дает огромную ошибку), поэтому коптер не гасит начальную скорость и не возвращается в начальную позицию.
Для решения этой задачи MIT, например, использует камеры и метки на своих коптерах.
Дополнительные материалы и источники
- Бранец В.Н., Шмыглевский И.П. «Применение кватернионов в задачах ориентации»
- Yaguang Yang «Analytic LQR Design for Spacecraft Control System Based on Quaternion Model»
- Ветка модифицированной прошивки на github
P.S. К сожалению, не могу поделиться моделью, а так же рассказать о расширенной модели с автопилотом и координатной стабилизацией в силу того, что это является частью моего будущего диплома, а все дипломы теперь проверяются на новизну и антиплагиат.
P.P.S. Я публикую данную статью на хабре, а не на новом GT в связи с тем, что остальные мои статьи схожей тематики остались именно на хабре.
Автор: Spin7ion







