После перехода на SQL Server с Oracle удивляет многое. Трудно привыкнуть к автоматическим транзакциям – после update не нужно набирать commit (что приятно), зато в случае ошибки не сможешь набрать rollback (что просто кошмарно). Трудно привыкнуть к архитектуре, в которой журнал используется и для отката, и для наката транзакций. Трудно привыкнуть к ситуации «писатель блокирует читателей, читатель блокирует писателей», а когда привыкнешь – ещё труднее отвыкнуть. И совсем не последнее место в рейтинге трудностей играет засилье кластеризованных индексов. По умолчанию первичный ключ таблицы – именно кластеризованный индекс, и поэтому почти у всех таблиц он есть.
На самом деле зверь этот совсем нестрашный и даже очень полезный. Давайте попробуем разобраться, зачем он нужен и как его использовать.
Файлы, страницы, RID
Данные любой таблицы физически сохранены в файле базы данных. Файл БД делится на страницы (page) – логические единицы хранения для сервера. Страница в MS SQL Server обязательно имеет размер 8 килобайт (8192 байта), из них под данные отдано 8060 байт. Для каждой строки можно указать её физический адрес, так называемый Row ID (RID): в каком файле она находится, в какой по порядку странице этого файла, в каком месте страницы. Страницу таблица присваивает целиком – на одной странице могут быть данные только одной таблицы. Более того, при необходимости считать/записать строку сервер считывает/записывает всю страницу, поскольку так получается гораздо быстрее.
Как устроен B-tree индекс?
B-tree означает balanced tree, «сбалансированное дерево». Индекс содержит ровно одну корневую страницу, которая является точкой входа для поиска. Корневая страница содержит значения ключей и ссылки на страницы следующего уровня для данных значений индекса. При поиске по индексу находится последнее значение, которое не превосходит искомое, и происходит переход на соответствующую страницу. На последнем, листьевом уровне дерева перечислены все ключи, и для каждого из них указана ссылка (bookmark) на данные таблицы. Естественным кандидатом на роль ссылки является RID, и он в самом деле используется в этом качестве для случая кучи. На следующем рисунке буквы B обозначают ссылки на строки таблицы.
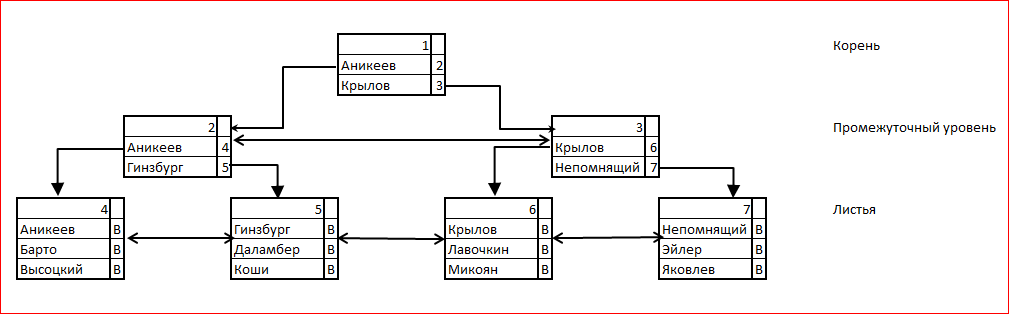
При добавлении записи в таблицу её необходимо также добавить в индекс. Новая запись индекса, ссылающаяся на запись таблицы, вставляется в страницу листьевого уровня. При этом может оказаться, что на этой странице нет свободного места. Тогда:
- Индексу выделяется новая страница – тоже на листьевом уровне.
- Половина записей из прежней страницы переносится на новую (чтобы при последовательном добавлении не напороться на ситуацию, когда для следующей строки снова придётся выделять страницу). Новая страница встраивается в горизонтальные ссылки: вместо Прежняя ↔ Следующая настраиваются ссылки Прежняя ↔ Новая ↔ Следующая.
- В родительскую страницу заносится ссылка на новую страницу, снабжённая соответствующим ключом. При этом может переполниться и родительская страница – тогда процесс разделения данных повторится на более высоком уровне. Если переполнение дойдёт до самого верха, то разделится надвое корневая страница, и появится новый корень, а высота дерева увеличится на 1.
Понятно, что добавление записей в таблицу при наличии индекса становится заметно более дорогостоящим процессом – каждое разбиение страницы требует обновления как минимум 4 страниц (разделяемую, следующую за разделяемой, новую, родительскую).
При этом наличие индекса резко ускоряет поиск данных: вместо сплошного сканирования можно вести двоичный поиск, спускаясь по дереву. Также за счёт наличия горизонтальных ссылок на страницы одного уровня пройти диапазон ключей индекса можно очень быстро. И мы плавно подходим к основным задачам выборки: поиск одного значения и сканирование диапазонов.
Куча мала
Рассмотрим некоторую модельную таблицу, организованную в виде кучи: какого-то определённого порядка в записях нет.
RID, который запись получает в самом начале, остаётся с ней почти всегда. В редких случаях записи в куче могут перемещаться на другую страницу – это происходит, когда после обновления строка перестаёт помещаться на то место, которое она занимала. Но в таком случае на прежнем месте остаётся ссылка на новое размещение – то есть, зная RID, полученный строкой при добавлении, строку можно найти всегда. Поэтому для индексов на куче наилучший выбор для ссылки на данные – именно RID.
Предположим, в таблице 200 тысяч записей, и в каждую страницу помещается от 48 до 52 записей. Будем считать, что таблица занимает 4000 страниц. Допустим, нам нужно найти все записи, в которых поле [City] имеет значение 'Perm'. Также допустим, что их всего 3, но мы об этом пока не знаем.
Серверу придётся просканировать все 4000 страниц. Даже если сервер найдёт все 3 записи, ему всё равно придётся идти до конца – ведь нет гарантии, что больше нужных записей нет. Итак, для выполнения запроса понадобится 4000 логических чтений страницы.
А если у нас есть индекс, в котором можно искать двоичным поиском – скажем, дерево высоты 3? Тогда серверу потребуется 3 чтения индексных страниц для того, чтобы найти адрес первой записи. Адреса второй и третьей записей будут лежать рядом – либо в той же странице, либо в следующей: страницы индекса по горизонтали соединены ссылками. То есть после максимум 4 чтений сервер наверняка знает RID всех трёх записей. Если сильно не повезёт, все 3 записи лежат в разных страницах. Таким образом, при наличии индекса после 7 логических чтений страницы все 3 записи наверняка будут найдены. 7 против 4000 – впечатляет.
Но так хорошо будет, когда записей мало. А если это не 'Perm', а 'Moscow', и нужных записей не 3, а 20 тысяч? Это не очень много, всего 10 процентов от общего количества записей. Но картина быстро становится не столь радужной.
За 3 чтения сервер найдёт первую запись. А затем ему потребуется считать 20 тысяч RID и 20 тысяч раз прочитать страницу, чтобы получить строку: мы помним, что сервер читает данные только целыми страницами. Вполне может получиться так, что нужные записи рассеяны по всей таблице, и для обеспечения 20 тысяч логических чтений потребуется считать большую часть страниц с диска. Ещё хорошо, если не все. Вместо 4 тысяч логических чтений мы получаем 20 тысяч.
Индекс очень хорошо работает на поиске небольшого количества значений, но плохо работает на прохождении больших диапазонов.
Оптимизатор запросов прекрасно осведомлён об этом. Поэтому если он ожидает, что поиск по индексу даст достаточно большой диапазон, вместо поиска по индексу он выберет полное сканирование таблицы. Это, кстати, одно из редких мест, где Оптимизатор может ошибиться, даже имея правильные статистики. Если на самом деле требуемые данные расположены очень компактно (например, 20 тысяч логических чтений – это 60 раз прочесть блок с диска и 19940 раз прочесть блок в кэше), то принудительное использование индекса даст выигрыш в памяти и в скорости.
А как же быть с диапазонами?
Проблема именно в том, что в конце поиска по индексу сервер получает не данные, а только адрес, по которому они лежат. Серверу ещё нужно идти по этому адресу и брать данные оттуда. Вот было бы здорово, если бы в конце пути сразу лежали данные!
Некоторые, собственно, и лежат. Значения ключей, например, лежат именно в индексе – за ними идти не нужно. Только за неключевыми полями. А что будет, если неключевые поля тоже положить в индекс? Ну допустим, не все, а только те, которые нужны сканирующему запросу?
А будет в таком случае индекс с добавочными (included) столбцами. Он проигрывает обычному индексу по размеру: его листьевые страницы содержат не только ключи и адреса строк, но и часть данных. В поиске одиночного значения такой индекс работает не хуже, а в сканировании диапазонов – намного, намного лучше. Если индекс покрывает запрос (то есть содержит все столбцы, перечисленные в запросе), то для выполнения запроса таблица не нужна вообще. Возможность взять все требуемые данные из индекса, не обращаясь к закладкам, даёт громадный выигрыш.
Вернёмся к нашему модельному примеру. Предположим, что требуемые для запроса столбцы включены в индекс. Для простоты предположим, что в листьевую страницу индекса попадают ровно 50 записей (ключи, добавленные столбцы, ссылки на записи). Тогда сканирование 20 тысяч записей потребует чтения всего лишь 400 страниц индекса – вместо 20 тысяч логических чтений для непокрывающего индекса.
400 против 20 тысяч – разница в 50 раз. Оптимизатор запросов недаром любит предлагать включить в индекс те или иные столбцы.
А может, стоит добавить в индекс все столбцы? Тогда любой запрос будет покрыт индексом обязательно. Более того, тогда в листьях даже не нужны RID, потому что ни за какими данными такой индекс не будет обращаться в таблицу, у него всё под рукой. Да в таком случае становится не нужна и сама таблица!
И мы пришли к концепции кластеризованного индекса. Он устроен как обычное B-дерево, но в его листьевых страницах вместо ссылок на записи таблицы расположены сами данные, а отдельной от него таблицы больше нет. Таблица не может иметь кластеризованный индекс, она может быть кластеризованным индексом.
Любое сканирование по ключу в кластеризованном индексе будет лучше, чем полный просмотр таблицы. Даже если просканировать нужно 97% всех записей.
Где подвох?
Первый – понятно где. Кластеризованный индекс – это таблица, а таблица может быть только одна. Сервер должен иметь мастер-копию данных, и только из одного индекса он готов выбросить все закладки и оставить только сами данные. Если есть ещё один индекс, в который включены все поля – в нём всё равно будут и адреса строк.
Есть и второй подвох. При наличии кластеризованного индекса в качестве адреса строки уже нельзя использовать RID. Записи в кластеризованном индексе отсортированы (физически – в пределах страницы, логически – горизонтальными ссылками между страницами). При добавлении записи или изменении ключевых полей запись перемещается в правильное место – часто в пределах страницы, но возможно и перемещение на другую страницу. Иными словами, RID в кластеризованном индексе перестаёт идентифицировать запись однозначно. Поэтому в качестве адреса строки, однозначно её идентифицирующего, используется ключ кластеризованного индекса.
То есть при поиске в некластеризованном индексе после прохода по его дереву мы получаем не адрес данных, а ключ кластеризованного индекса. Для получения самих данных нужно пройти дерево кластеризованного индекса тоже.
Представим себе сканирование диапазона в 20 тысяч записей по некластеризованному индексу, построенному на кластеризованном. Теперь понадобится выполнить не 20 тысяч логических чтений страницы по известному RID, а 20 тысяч поисков в кластеризованном индексе – и каждый поиск потребует 3, а то и более, логических чтений.
А если ключ кластеризованного индекса не уникален? А так не бывает. Для сервера он обязательно уникален. Если пользователь попросил создать неуникальный кластеризованный индекс, сервер к каждому ключу припишет 4-байтовое целое число, которое обеспечит уникальность ключа. Делается это прозрачно для пользователей: сервер не только не сообщает им точного значения числа, но и не выдаёт сам факт его наличия. Уникальность ключа нужна именно для возможности однозначной идентификации записей – чтобы ключ кластеризованного индекса мог служить адресом строки.
Так делать или не делать?
Вооружённые теорией, мы можем описать рациональную процедуру построения кластеризованного индекса. Следует выписать все индексы, которые нужны таблице, и выбрать из них кандидата на кластеризацию.
Не нужно делать кластеризованный индекс только для того, чтобы он был. Если по ключу индекса не предполагается сканирование – это не очень хороший кандидат для кластеризации (если по другим индексам сканирование предполагается – то даже очень плохой кандидат). Неправильный выбор кандидата на кластеризацию ухудшит производительность, потому что все остальные индексы станут работать хуже, чем работали на куче.
Предлагается следующий алгоритм выбора:
- Определить все индексы, по которым происходит поиск одиночного значения. Если такой индекс единственный – его и нужно кластеризовать. Если несколько – перейти к следующему шагу.
- Добавить к индексам с предыдущего шага все индексы, по которым предполагается сканирование диапазонов. Если таковых нет – кластеризованный индекс не нужен, несколько индексов на куче будут работать лучше. Если есть – каждый из них следует сделать покрывающим, добавив все столбцы, которые нужны сканирующим запросам по этому индексу. Если такой индекс единственный – его следует кластеризовать. Если их больше одного – перейти к следующему шагу.
- Однозначно лучшего выбора кандидата на кластеризацию среди всех покрывающих индексов нет. Следует кластеризовать какой-то из этих индексов, принимая во внимание следующее:
- Длина ключа. Ключ кластеризованного индекса является ссылкой на строку и хранится на листьевом уровне некластеризованного индекса. Меньшая длина ключа означает меньше места на хранение и более высокую производительность.
- Степень покрытия. Кластеризованный индекс содержит все поля «бесплатно», и покрывающий индекс с самым большим набором полей – хороший кандидат на кластеризацию.
- Частота использования. Поиск одиночного значения в покрывающем индексе – самый быстрый возможный поиск, а кластеризованный индекс – покрывающий для любого запроса.
Постскриптум. Почему он единственный?
Когда я начинал писать эту статью – я прекрасно понимал, почему у таблицы не может быть больше одного кластеризованного индекса. В середине написания я понимать это перестал и теперь уже не понимаю (хотя, что смешно, по-прежнему могу это объяснить). Сейчас у меня есть только гипотезы.
Кластеризованный индекс, во-первых, содержит все данные в листьевых вершинах, а во-вторых, не содержит никаких ссылок на данные таблицы (потому что никакой внешней по отношению к нему таблицы нет). Ну и что мешает завести несколько так устроенных индексов – содержащих все поля и не содержащих ссылки? Я не знаю. Могу только предложить.
Прежде всего – мы же можем завести сколько угодно индексов, в которые будут включены все поля. Значит, весь выигрыш, который нам сулит наличие нескольких кластеризованных индексов, относительно невелик: на листьевом уровне добавочных индексов не будет ссылок на данные, то есть мы сэкономим немного места. А какие проблемы повлечёт за собой создание нескольких кластеризованных индексов?
- Ключи кластеризованного индекса представляют собой ссылки на данные, которые хранятся в листьях некластеризованных индексов. Если бы кластеризованных индексов могло бы быть несколько, среди них всё равно пришлось бы выделять «основной», тот, ключи которого являются идентификаторами данных.
- Если в кластеризованный индекс нужно добавить неключевой столбец, то индекс придётся полностью перестроить, а некластеризованные индексы на нём не нужно менять вообще. Если бы кластеризованных индексов было несколько, перестраивать пришлось бы все, и невозможно было бы заранее определить, сколько времени это бы заняло.
- Возникло бы множество ситуаций, чреватых ошибками. Например, если при наличии нескольких кластеризованных индексов пользователь удаляет мастер-индекс (тот, ключи которого служат ссылками на данные в некластеризованных индексах), то серверу придётся автоматически выбрать новый мастер-индекс.
Сейчас я склоняюсь к мысли, что запрет множественных кластеризованных индексов связан с тем, что реализация этой концепции затратна и чревата ошибками (то есть понижением надёжности), а выгод принесла бы относительно мало. Иными словами, сделать несколько кластеризованных индексов технически можно, но дорого, неудобно и ни к чему.
Возможно, что я не вижу какие-нибудь соображения, вследствие которого делать несколько кластеризованных индексов нельзя. Буду очень признателен, если кто-то укажет мне эти соображения.
Удачи всем в кластеризации ваших индексов!
Автор: Yggaz






