Удивительно быстрые алгоритмы

в 14:04, , рубрики: Алгоритмы, динамическое программирование

Изучая программирование я встречаю примеры невозможных алгоритмов. Интуиция говорит, что такого не может быть, но компьютер опровергает её простым запуском кода. Как такую задачу, требующую минимум кубических затрат по времени, можно решить всего за квадрат? А вон ту я точно решу за линию. Что? Есть гораздо более эффективный и элегантный алгоритм, работающий за логарифм? Удивительно!

В этой статье я приведу несколько таких "ломающих шаблоны" алгоритмов, показывающих что интуиция может сильно переоценивать временную сложность задачи.

Интересно? Добро пожаловать под кат!

Вычисление n-го элемента реккурентной последовательности за логарифм

Под "реккурентной" я понимаю последовательность, удовлетворяющую следующему уравнению:

$ a_{n+k+1}=sum_{i=1}^{k} c_{i} a_{n + i} $

Первые $k$ элементов последовательности считаются заданными. Число $k$ называется мощностью последовательности, а $c_i$ коэффициентами последовательности. Типичный пример: числа Фибонначи, где $a_1=0$, $a_2=1$, $c_1=1$, $c_2=1$. Получаются всем известные числа: 0, 1, 1, 2, 3, 5, 8, 13,… Вроде бы никакой сложности нет вычислять n-ный элемент за линию, но оказывается это можно делать за логарифм!

Идея: а что, если представить вычисление $a_n$ как возведение в $n$-ю степень какого-нибудь объекта? Возводить в степень можно за логарифм, только что это будет за объект? Вообще, что нужно знать для вычисления $a_{n+2}$? Только $a_n$ и $a_{n+1}$. Значит этот объект, чем бы он ни был, должен содержать эти два числа. Ещё должен быть какой-то "естесственный" способ перемножать эти объекты. Ничего не напоминает? Очень похоже на матрицы: они составлены из чисел и их можно перемножать! Но есть ли такая матрица, перемножая которую с самой собой, мы будет последовательно получать числа Фибонначи?

Оказывается, есть! Вот она:
wake up, Neo
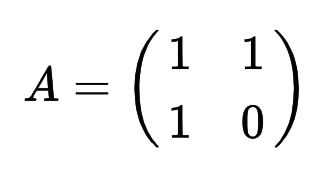
Можете сами проверить и убедиться, что $a_{n+1}=A^n_{1,1}$. Удивительно, но это работает!

Теперь посмотрим, сможем ли мы обобщить этот случай на любую реккурентную последовательность? Почему это сработало в случае Фибонначи? Очевидно, выполняет следующее тождество:

$$display$$ begin{equation*} begin{pmatrix} f_{n+1} & f_n \ f_n & f_{n-1} end{pmatrix} times begin{pmatrix} 1 & 1 \ 1 & 0 end{pmatrix} = begin{pmatrix} f_{n+2} & f_{n+1} \ f_{n+1} & f_n end{pmatrix} end{equation*} $$display$$

Всё дело в том, что "скалярное произведение" первой строчки левой и первого столбца правой матрицы как раз и вычисляет следующий элемент последовательности. Остальные просто копируются из исходной. Назовём такую матрицу $A$ генератором реккурентной последовательности. Попробуем посчитать таким образом последовательность "трибонначи":

$ t_1=1 \ t_2=1 \ t_3=1 \ ... \ t_{n+3}=t_{n+2} + t_{n+1} + t_n $

За генератор можно взять матрицу $A$:

$$display$$ begin{equation*} begin{pmatrix} 1 & 1 & 0 \ 1 & 0 & 1 \ 1 & 0 & 0 end{pmatrix} end{equation*} $$display$$

Почему именно такую? Понятно, что первый столбец должен состоять из коэффициентов реккуренного уравнения. В остальных единицы должны располагаться так, чтобы копировать нужные элементы. Получается следующее тождество:

$$display$$ begin{equation*} begin{pmatrix} t_{n+2} & t_{n+1} & t_n \ t_{n+1} & t_n & t_{n-1} \ t_n & t_{n-1} & t_{n-2} end{pmatrix} times begin{pmatrix} 1 & 1 & 0 \ 1 & 0 & 1 \ 1 & 0 & 0 end{pmatrix} = begin{pmatrix} t_{n+3} & t_{n+2} & t_{n+1} \ t_{n+2} & t_{n+1} & t_n \ t_{n+1} & t_n & t_{n-1} end{pmatrix} end{equation*} $$display$$

Выходит, в качестве первой матрицы $T$ надо взять:

$$display$$ begin{equation*} begin{pmatrix} t_5 & t_4 & t_3 \ t_4 & t_3 & t_2 \ t_3 & t_2 & t_1 end{pmatrix} = begin{pmatrix} 3 & 1 & 1 \ 1 & 1 & 1 \ 1 & 1 & 0 end{pmatrix} end{equation*} $$display$$

Тогда $t_{n+2}=(T times A^{n - 1})_{1, 1}$. Благодаря ассоциативности матричного умножения матричного умножения, мы можем сначала вычислить возведение $A$ в $n - 1$ степень, а потом уже перемножить $T$ и $A$. В случае Фибонначи $T$ совпадало с $A$.

Получается, общий вид генератора для реккурентной последовательности мощности $k$ будет иметь вид:

$$display$$ begin{equation*} begin{pmatrix} c_1 & 1 & 0 & 0 & cdots & 0 \ c_2 & 0 & 1 & 0 & cdots & 0 \ c_3 & 0 & 0 & 1 & cdots & 0 \ vdots & vdots & vdots & vdots & ddots & vdots \ c_{k-1} & 0 & 0 & 0 & cdots & 1 \ c_k & 0 & 0 & 0 & cdots & 0 end{pmatrix} end{equation*} $$display$$

Начальная матрица, на которую умножается генератор, содержит первые $2k - 1$ элементов последовательности, расположенные в "пирамидном" порядке.

Понятно, что такой алгоритм будет работать за $O(k^3 log n)$ по времени: каждое умножение матриц выполняется за $O(k^3)$, а всего $O(log n)$ таких умножений. Кубический множитель играет важную роль. Например, в случае Фибонначи, преимущество нашего алгоритма над линейным достигается только при $n ge 44$, а в случае Трибонначи вообще при $n ge 208$. Однако значение множителя можно понизить если в рекурсивном алгоритме возведения в степень делить не на два случая чётнечёт как обычно, а на три. Тогда в основании логарифма будет тройка, что понизит преимущество до $n ge 118$.

Следующий класс Matrix содержит методы умножения и возведения в степень квадратных матриц:

class Matrix:
    def __init__(self, n):
        self.n = n
        self.rows = [[0 for col in range(n)] for row in range(n)]

    def set(self, row, col, value):
        self.rows[row][col] = value

    def get(self, row, col):
        return self.rows[row][col]

    def __str__(self):
        result = ''
        for row in self.rows:
            result += ' '.join([str(col) for col in row])
            result += 'n'
        return result

    def __mul__(self, other):
        result = Matrix(self.n)
        for row in range(self.n):
            for col in range(self.n):
                s = sum([self.get(row, k) * other.get(k, col) for k in range(self.n)])
                result.set(row, col, s)
        return result

    def __len__(self):
        return self.n

    def __pow__(self, k):
        if k == 0:
            result = Matrix(len(self))
            for i in range(len(self)):
                result.set(i, i, 1)
        elif k == 1:
            result = self
        elif k == 2:
            result = self * self
        else:
            rem = k % 3
            prev = self.__pow__((k - rem) // 3)
            result = prev * prev * prev
            if rem:
                result *= self.__pow__(rem)
        return result

Внимание на метод __pow__: это определение операции M ** k, где M это объект класса Matrix. Он вычисляет её, рекурсивно разбивая каждый вызов на три кейса в зависимости от остатка от деления на 3. Это позволяет уменьшить константу времени работы алгоритма.

Определим наши $T$ и $A$ для Трибонначи, пользуясь Matrix:

A = Matrix(3)
A.set(0, 0, 1)
A.set(0, 1, 1)
A.set(1, 0, 1)
A.set(1, 2, 1)
A.set(2, 0, 1)
T = Matrix(3)
T.set(0, 0, 3)
T.set(0, 1, 1)
T.set(0, 2, 1)
T.set(1, 0, 1)
T.set(1, 1, 1)
T.set(1, 2, 1)
T.set(2, 0, 1)
T.set(2, 1, 1)
T.set(2, 2, 0)
n = int(sys.argv[1])
if n:
    print(T * A ** (n - 1))
else:
    print(T ** 0)

Этот код принимает аргумент $n$ — номер элемента последовательности Трибонначи, который мы хотим вычислить. Вот и всё, добавлю только, что такой алгоритм можно обобщить на нечисловые последовательности, нужно только чтобы элементы принадлежали какому-нибудь Кольцу. Упрощённо, это математическая структура, в которой определены сложение и умножение над произвольным множеством объектов.

Вычисление подмассива наибольшей длины за линию

Вторая задача звучит так: дан массив целых чисел A[1..n] (для простоты считаем что индексы идут с единицы). Надо найти подмассив A[i..j] с наибольшей суммой. В подмассиве присутствуют все элементы от i до j включительно. Эта задача интересна тем, что для неё существуют алгоритмы с временной сложностью $O(n^3)$, $O(n^2)$, $O(n log n)$ и даже $O(n)$.

Вкратце идея каждого алгоритма:

  1. Куб. Пройтись по всем подмассивам, каждый раз высчитывая их сумму заново. Получается три вложенных цикла. Самый простой, но самый медленный вариант.
  2. Квадрат. Пройтись по всем подмассивам, сохраняя текущую сумму.
  3. $O(n log n)$. Разбить массив пополам, рекурсивно рассмотреть три случая: искомый ответ полностью лежит в левой части, между ними, либо в правой.
  4. $O(n)$. Завести новый массив T[1..n], где i-тый элемент равен наибольшей сумме подмассива, оканчивающегося в i. Оказывается, можно считать $T$ за линию, а конечным ответом будет наибольшее из $T$. Это так называемый алгоритм Кадана

Нам интересен последний вариант. Давайте подумаем, как найти T[i + 1], зная T[i]? Если мы знаем сумму наибольшего подмассива, оканчивающегося в i, то следующий элемент может либо расширять его, либо начать новый подмассив. Действительно, T[i + 1] может быть либо T[i] + A[i + 1], либо A[i + 1], либо 0, если A[i + 1] < 0. Получаем реккурентную формулу:

T[0] = 0,
T[i + 1] = max{T[i] + A[i + 1], A[i + 1], 0} = max{T[i] + A[i + 1], 0}

Докажем последнее равенство. Понятно, что T[i] >= 0 для любого i. Пусть k = A[i + 1]. Рассмотрим три случая:

  1. k < 0. Тогда 0 превзойдёт k в первом max.
  2. k = 0. В первом max можно просто убрать второй аргумент.
  3. k > 0. Тогда max{T[i] + k, k, 0} = T[i] + k = max{T[i] + k, 0}.

Благодаря линейности и простоте уравнения, алгоритм получается совсем коротким:

def kadane(ints):
    prev_sum = 0
    answer = -1
    for n in ints:
        prev_sum = max(prev_sum + n, 0)
        if prev_sum >= answer:
            answer = prev_sum
    return answer

Заключение

В обоих задачах качественно повысить производительность нам помогла техника динамического программирования. Это не случайно, динамика часто даёт асимптотически оптимальные алгоритмы благодаря встроенной экономии: мы считаем всё только один раз.

А какие вы знаете удивительные алгоритмы?

Автор: Евгений Грязнов

Источник

* - обязательные к заполнению поля

Главная   |  Архив новостей  |   Android  |   Google  |   Apple  |   Microsoft  |   Информационная безопасность  |   Веб – разработка
Публикации RSS  |  Комментарии RSS
https://ajax.googleapis.com/ajax/libs/jquery/3.4.1/jquery.min.js