Программирование необычных шахмат

Написание своего шахматного движка - обширная тема, про которую пишут целые книги.

Однако очень многие шахматные программы работают со "стандартными" правилами шахмат и не могут работать при других правилах, хотя существуют сотни вариаций шахмат.

В этой заметке я покажу, каким образом можно написать достаточно быстрый и гибкий шахматный движок на С++, в котором можно задавать произвольный размер доски, расположение фигур, и создавать новые типы шахматных фигур.

Я запрограммировал 15 шахматных вариаций - для каждой опишу неожиданные ходы и результаты партий компьютера друг с другом.

Другие шахматные движки

Прежде чем сделать что-то свое, надо понять, как работают другие шахматные движки.

Есть Вики, посвященная программированию шахмат - https://www.chessprogramming.org/. В ней описаны основные концепции - представление доски, поиск, оценка позиции, базы дебютов и эндшпилей.

На Хабре по теме можно почитать эту отличную статью - https://habr.com/ru/post/329528/, там также покрыты важные темы.

Каждую концепцию в движке можно обсудить по порядку. Для реализации я использовал язык программирования C++.

Представление доски (часть 1)

Первое, что нужно обдумать - каким образом мы будем представлять доску (т.е. позицию в шахматной игре)?

"Доска" это объект, который должен закодировать в себе такую информацию:

• Местоположение фигур

• "Память" фигур: для пешек - можем ли походить на 2 шага вперед, может ли пешка быть взята на проходе; для короля - право на рокировку, и т.д.

• Кто сейчас ходит: белые или черные (но это не обязательно, в моем движке "доска" про это не знает)

Так как в процессе поиска лучшего хода перебирается сумасшедшее количество досок, нужно сразу сделать их так, чтобы они как можно быстрее работали.

Не будем тратить время на очевидно неоптимальные варианты (например, хранение фигур в виде списка std::list).

Я выбрал путь bitboard - это когда каждая клетка доски представлено одним числом. Для стандартной доски 8x8 это будет массив из 64 чисел. Таким образом, вся доска занимает цельный участок в памяти на стеке, что довольно важно для быстродействия движка.

В статье на Хабре (на которую ссылался в прошлом разделе) показано, что в стандартных шахматах хватает 14 бит на клетку (значит, тип числа может быть short или int). У каждого бита есть свое значение, в случае той статьи это AHIIIIEWB0MFFF, где F - тип фигуры, A - была ли длинная рокировка, и так далее. Это представление жестко привязано к существующим шахматным правилам и для шахмат с другими правилами не годится (конечно, такой задачи и не стояло, это просто констатация факта).

Bit storage

Так как каждая клетка на доске будет закодирована в одном числе, мы должны уметь удобно управлять битами в этом числе.

Для этого можно сделать "битовый контейнер".

В моей реализации тип для "битового контейнера" должен быть целочисленным: concept TPossibleStorageType.

"Битовый контейнер" работает поверх одного числа: class TBitStorage.

Как видим, у "контейнера" можно запросить хэндлер над группой последовательных битов (GetView()), и через него читать/записывать в биты значения без ручной возни с битовыми сдвигами: class TBitView.

В юнит-тестах к "контейнеру" можно посмотреть, как происходит работа с ним.

Представление фигуры

В моей реализации для bitboard используются 32-битные целые числа: class TPiece.

Этот объем предназначен для хранения данных. Каждый под-класс класса TPiece будет определять сам, какие данные он хочет хранить: для короля это возможность рокировки, для пешки это возможность походить на 2 клетки вперед, и так далее.

Как выглядит определение фигуры, можно посмотреть на примере пешки class TPawnPiece:

• Константы: id фигуры, стоимость фигуры, символы для вывода в консоль, изображения.

• "Память" фигуры: у пешки есть 4 состояния (т.е. для их записи достаточно 2 битов), на основании которых проверяется возможность взятия на проходе и хода на 2 клетки вперед. Вообще "память" это редкое свойство, в подавляющем большинстве фигуры (в том числе из нестандартных шахмат) всегда двигаются одинаково.

• Генерация ходов: об этом будет свой раздел ниже.

• Регистрация класса фигуры: техническая вещь, чтобы по piece id можно было получить данные класса.

Хоть мы и используем всего лишь одно 32-битное число, понятно что нет такой фигуры, которая действительно сможет утилизировать такой объем данных. То есть старшие биты числа всегда будут неиспользуемыми.

Особенность таких "битовых контейнеров" в том, что их можно "упаковать" внутрь других битовых контейнеров.

Например, чтобы использовать более оптимальный аналог std::optional<TPawnPiece>, можно завести другой 32-битный битовый контейнер, где нулевым битом будет флаг "пустоты", а начиная с первого бита будет исходный битовый контейнер. Посмотрите как сделан class TPieceOrEmpty<T>.

Представление доски (часть 2)

Каждая клетка доски, как уже упоминалось, должна быть представлена в виде 32-битного числа.

Для этого создан битовый контейнер class TBoardPiece, его состав:

• 1 бит - цвет фигуры (если есть).

• 10 битов - id фигуры (если клетка пустая, то эти биты равняются 0).

• остальные биты - битовый контейнер фигуры (то есть какой-нибудь подкласс TPiece).

Сама доска представляется так:

using TBoardPiecesContainer = std::array<TBoardPiece, 64>;

То есть это массив из объектов TBoardPiece.

Для объекта доски можно сделать удобные методы для обновления клеток: class TBoard.

Для позиции есть своя структура:

struct TBoardPosition {
    int Column;
    int Row;
};

Дамп доски в поток вывода

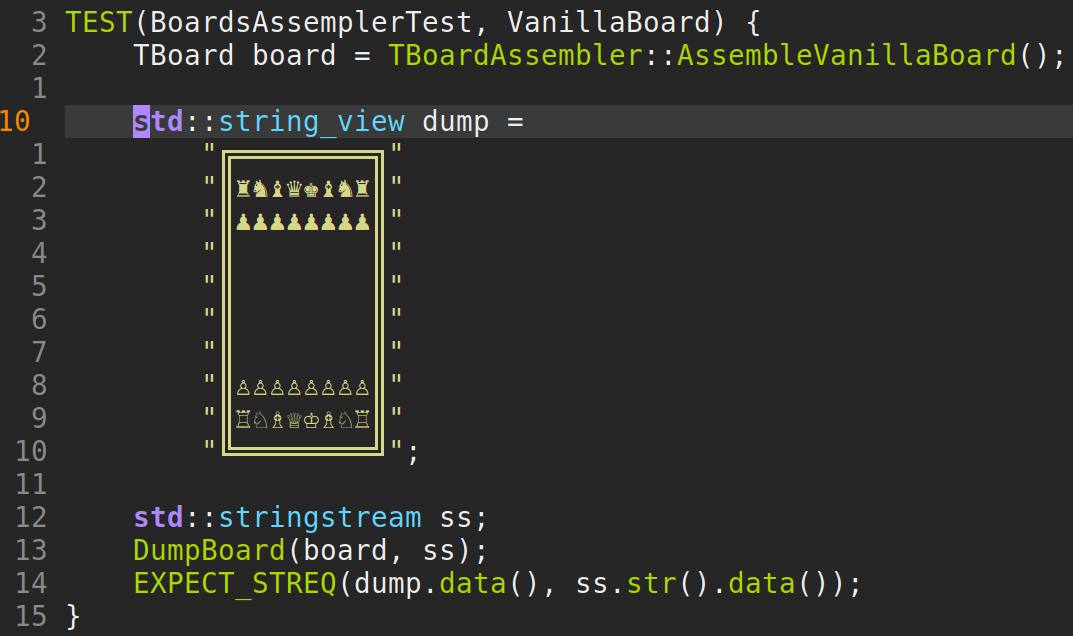
Желательно писать тестируемый код. На данный момент в программе 77 юнит-тестов. Так как проверять позицию на доске через список фигур очень неудобно, я это делаю через дамп доски в поток вывода (в тестах это std::stringstream). Стандартная доска дампится в такую строку (в моем редакторе кода зазоров между строк нет):

╔════════╗
║♜♞♝♛♚♝♞♜║
║♟︎♟︎♟︎♟︎♟︎♟︎♟︎♟︎║
║        ║
║        ║
║        ║
║        ║
║♙♙♙♙♙♙♙♙║
║♖♘♗♕♔♗♘♖║
╚════════╝

Таким методом можно достаточно просто тестировать всё, что связано с разными позициями (расстановку фигур, генерацию ходов, выбор лучшего хода, ...). Также дамп можно писать в консоль во время игры компьютера с самим собой.

Основы генерации ходов

В первую очередь нужно понять - что такое "ход", что меняется после его свершения? Один "ход" это несколько "обновлений". Одно "обновление" заменяет в какой-то клетке одну фигуру на другую. Как обычно, сразу сделаем достаточно оптимизированный вариант - держим все "обновления" на стеке (а не в std::vector/std::list):

struct TBoardUpdate {
    TBoardPosition Position;
    TBoardPiece NewBoardPiece;
};

struct TMove {
    std::array<TBoardUpdate, 10> Updates;
    std::size_t UpdatesCount = 0;
};

Тут мы рассчитываем, что за один ход не будет больше 10 обновлений.

В генерации ходов можно столкнуться с проблемой - у белых и у черных фигур разная "точка зрения": у белых пешка идет "вперед", а у черных она идет как бы "назад". Чтобы не дублировать код для двух цветов, надо создать class TOrientedBoardWrapper - обертку над объектом TBoard, которая проксирует метод GetBoardPiece с флагом инвертированности. Таким образом, генерацию ходов надо писать один раз, с "точки зрения белых".

Ходы (struct TMove) нужно хранить в каком-нибудь контейнере. Немного забегая вперед - иногда движку нужно знать не все ходы, а только их количество. Поэтому "контейнер" выглядит в виде интерфейса так:

struct IMoveContainer {
    ~IMoveContainer() = default;
    virtual void Add(const TMove& move) = 0;
    virtual void InverseMoves(const TBoard& board) = 0;
};

Метод Add добавляет ходы, метод InverseMoves инвертирует позиции во всех "обновлениях" в зависимости от размера доски.

У интерфейса есть две реализации - один действительно сохраняет ходы, другой только их количество:

struct TMoveContainer : IMoveContainer {
    std::array<TMove, 128> Moves;
    std::size_t MovesCount = 0;

    void Add(const TMove& move) override {
        Moves[MovesCount++] = move;
    }
    void InverseMoves(const TBoard& board) override;
};

struct TDummyMoveContainer : IMoveContainer {
    std::size_t MovesCount = 0;

    void Add(const TMove& move) override {
        MovesCount++;
    }
    void InverseMoves(const TBoard& /* board */) override {}
};

Если собрать все, что фигуре нужно для того, чтобы сгенерировать ходы, получится такая структура:

struct TMoveContext {
    // new moves should be written here
    IMoveContainer& Moves;

    // used to "look around" to see other pieces
    TOrientedBoardWrapper Board;

    // additional info about current piece
    const TBoardPosition Position;
};

Поэтому для каждой фигуры, находящейся на поле, вызывается метод ее класса

void FillMoves(TMoveContext& moveContext);

В этом методе фигура должна добавлять ходы в контейнер.

Генерация ходов у стандартных фигур

Среди всех стандартных фигур самая сложная "бизнес"-логика - у пешек. Можно посмотреть код в TPawnPiece::FillMoves, где описывается генерация ходов. В процессе этого используется "память" фигуры и доска.

Если у фигуры определен метод AfterMoveApply, то он вызывается после того, как на доску "применится" новый ход. У пешки есть метод TPawnPiece::AfterMoveApply, который меняет "статус" пешки. Это связано с тем, что по правилу "взятий на проходе" пешку можно взять только сразу после хода, иначе право на такое взятие теряется.

Для стандартных типов ходов есть вспомогательный метод:

enum class EMoveType {
    Leaper,
    Rider,
    Hopper,
};
void AddStandardMoves(TMoveContext& ctx, TBoardPiece boardPiece, EMoveType moveType, TBoardPosition deltaPosition);

Тип хода Leaper - ходы как у коня: единичный фиксированный сдвиг на позицию.

Тип хода Rider - ходы как у слона/ладьи/ферзя: фигура может переместиться на определенный сдвиг сколько угодно раз, пока не встретит "препятствие" (край доски/другая фигура).

Все ходы проверяются на корректность: нельзя выпрыгнуть за край доски или съесть фигуру одного цвета.

Тип хода Hopper рассмотрим в следующий разделах - такой тип есть у "нестандартной" фигуры.

Вот так выглядит генерация ходов у коня:

void TKnightPiece::FillMoves(TMoveContext& moveContext) {
    TBoardPiece boardPiece = moveContext.Board.GetBoardPiece(moveContext.Position);
    for (int colMult : {-1, 1}) {
        for (int rowMult : {-1, 1}) {
            AddStandardMoves(moveContext, boardPiece, EMoveType::Leaper,
                             {.Column = colMult * 2, .Row = rowMult * 1});
            AddStandardMoves(moveContext, boardPiece, EMoveType::Leaper,
                             {.Column = colMult * 1, .Row = rowMult * 2});
        }
    }
}

Вот так у слона:

void TBishopPiece::FillMoves(TMoveContext& moveContext) {
    TBoardPiece boardPiece = moveContext.Board.GetBoardPiece(moveContext.Position);
    for (int colDelta : {-1, 1}) {
        for (int rowDelta : {-1, 1}) {
            AddStandardMoves(moveContext, boardPiece, EMoveType::Rider,
                             {.Column = colDelta, .Row = rowDelta});
        }
    }
}

Ходы покрыты тестами, например для слона: bishop_piece_ut.cc.

Оценка позиции

"Оценка позиции" это функция, которая определяет относительную "стоимость" доски.

На Chessprogramming Wiki можно почитать, как выглядят такие функции. Я выбрал для оценки простую функцию, которая выглядит так:

f(p) = 20000(K-K')
       + 900(Q-Q')
       + 500(R-R')
       + 300(B-B' + N-N')
       + 100(P-P')
       + 10(M-M')

K,Q,R,B,N,P - количество белых королей, ферзей, ладей,
              слонов, коней, пешек соответственно
K',Q',R',B',N',P' - то же самое у черных
M - мобильность (количество доступных ходов)

Этого достаточно, чтобы компьютер пытался "выводить" фигуры в бой, и предпринимал попытки победить противника и объявить мат. Так как функция целочисленная, то стоимость фигур делится на 100 (пешка стоит 100 баллов, ферзь стоит 900 баллов). Условно считается, что если у противника на одну пешку меньше, но возможных ходов на 10 больше, то позиции равноценны.

Для белых выгоднее, чтобы функция f(p) была как можно выше, для черных наоборот - как можно ниже.

Минимакс

Алгоритм поиска лучшего хода основан на "минимаксе". Допустим, что сейчас ход белых. Они должны выбрать наиболее оптимальный ход: чтобы f(p) был как можно выше через N ходов. Черные также выбирают ход оптимально: чтобы f(p) был как можно ниже.

Этот алгоритм достаточно известный, о нем подробнее можно почитать в статье "Минимакс на примере игры в зайца и волков".

Для быстрой игры минимакс жизненно необходимо оптимизировать, главным образом путем отсечения некоторых веток из поиска в глубину. Алгоритм поиска хода должен смотреть на N ходов вперед, чтобы "понимать", какие есть опасности или перспективы.

Если мы будем смотреть все возможные ходы, то далеко на этом уехать нельзя. В начале партии есть 20 доступных ходов. У ферзя на пустой доске есть 27 доступных ходов. Можно прикинуть, что число порядка растет очень быстро.

Описание всех факторов, влияющих на поиск:

Альфа-бета отсечение

Это стандартное отсечение, рассмотренное в статье про минимакс (чуть выше). Его суть в том, чтобы выкинуть из рассмотрения ветки поиска, которые гарантированно не улучшат результат.

Сортировка ходов по интересности

Успех альфа-бета отсечения еще зависит от того, насколько "хорошие" ходы мы рассматриваем в начале. Если быстро найти хороший ход, то остальные не такие хорошие ходы выкидываются почти сразу. Логично сделать быструю сортировку ходов по влиянию на стоимость фигур (без учета мобильности - ее "дорого" считать).

Сортировка в коде есть тут - ссылка.

Пролонгация поиска

Если в текущем ходе произошло взятие фигуры, то рассматривать все следующие ходы нужно, даже если достигнут "предел" глубины, так как обычно на взятие прилетает "ответка", то есть происходит обычный размен фигур. Если не продлевать поиск, то минимакс за горизонтом не увидит плохие последствия.

На пролонгацию поиска есть тест, где лучше понятно, что происходит. В "обычных" условиях, при поиске на глубину 1, если можно взять коня или ладью, то происходит взятие ладьи - minimax_ut.cc. Если взятая фигура защищена, то это влияет на поиск - minimax_ut.cc.

Однако для пролонгации по взятию есть свой отдельный предел глубины - если его не поставить, то поиск может смотреть хоть на 30 ходов вперед.

Ситуации, когда король под шахом, не пролонгируются, потому что определение шаха "дорогое", поэтому алгоритм избегает мата обычным образом (в пределах стандартной глубины).

Zobrist-хэширование

Zobrist hashing это хэширование всей доски в одно число (в моем случае 32-битное). Его особенность - похожие позиции должны иметь кардинально разный хэш.

Попытки добавить хэширование выпило мне много крови. Планировалось, что хэшировать можно уже рассмотренные в минимаксе доски (точнее, их оценку), чтобы не повторять работу по вычислению. В действительности компьютер после хэширования заметно отупел и выбирал плохие ходы. После дебага выяснилось, что из-за альфа-бета отсечения, где многие ходы на доске "в глубине" выбрасываются, в хэш попадала неправильная оценка. Все попытки добавить нормальный хэш провалились из-за неполного перебора.

Сейчас хэш используется, чтобы компьютер не делал повторяющиеся ходы, потому что в игре с самим собой он любит попадать в вечный цикл повторяющихся ходов - minimax.cc.

Неиспользованные оптимизации

Так как я не ставил целью победить популярные шахматные движки (как Stockfish), в программе нет других сложных оптимизаций. Оптимизации разделяются на две группы: оптимизация самого кода и отсечение дерева поиска. Обе группы я описал выше.

Из-за того, что шахматы будут не только "стандартные", в движке нет базы данных дебютов или особой логики для эндшпиля. То есть штуки, полагающиеся на стандартные шахматные правила, намеренно не внесены в движок.

Графика

Для отрисовки шахматной доски я использовал библиотеку SFML. Я сделал два режима - показ доски в окне, и сохранение в картинку. В этом деле нет ничего интересного для статьи.

Варианты шахмат

Всего запрограммировано 15 шахматных вариантов. В порядке возрастания необычности есть такие разновидности: обычные шахматы (1 вариант), обычные фигуры на обычной доске с необычным набором фигур (4 варианта), необычные фигуры на обычной доске (6 вариантов), необычная доска и фигуры (4 варианта). Список вариантов:

1. Стандартные шахматы (Vanilla Chess)

2. Атака легкой кавалерии (Charge of the Light Brigade)

3. Орда (Horde)

4. Крестьянское восстание (Peasants' Revolt)

5. Weak!

6. Беролина (Berolina)

7. Бешеный король (Mad King)

8. Тутти-фрутти (Tutti-Frutti)

9. Королевский конь (Knightmate)

10. Попрыгунчик (Grasshopper)

11. Атомные шахматы (Atomic)

12. Шахматы Капабланки (Capablanca Chess)

13. Антилопа Гну (Wildebeest)

14. Шахматы гарантированного возмездия (Stratomic)

15. Действительно большие шахматы (Really Big Board)

Эти варианты я взял с Википедии: https://en.wikipedia.org/wiki/List_of_chess_variants.

Также в Википедии доступен огромный список необычных шахматных фигур: https://en.wikipedia.org/wiki/Fairy_chess_piece.

По умолчанию движок рассматривает полный перебор для 4 ходов, пролонгация взятий действует еще на 6 дополнительных ходов. То есть "вперед" мы смотрим на 10 ходов (из них на первые 4 - в полном объеме). Это довольно много - попробуйте сделать 10 ходов на доске, чтобы почувствовать. Эта настройка выбрана в большинстве вариантов (если не указано иное).

Картинки партий (а также логи) для всех шахматных вариантов можно смотреть в репозитории движка в этой директории. Например, для стандартных шахмат это под-директория vanilla. В статье будут склейки по интересным местам (склейки кликабельны). Внимание - описание склейки находится под склейкой (чтобы не путаться)!

Стандартные шахматы (Vanilla Chess)

Запускаем игру компьютера с самим собой.

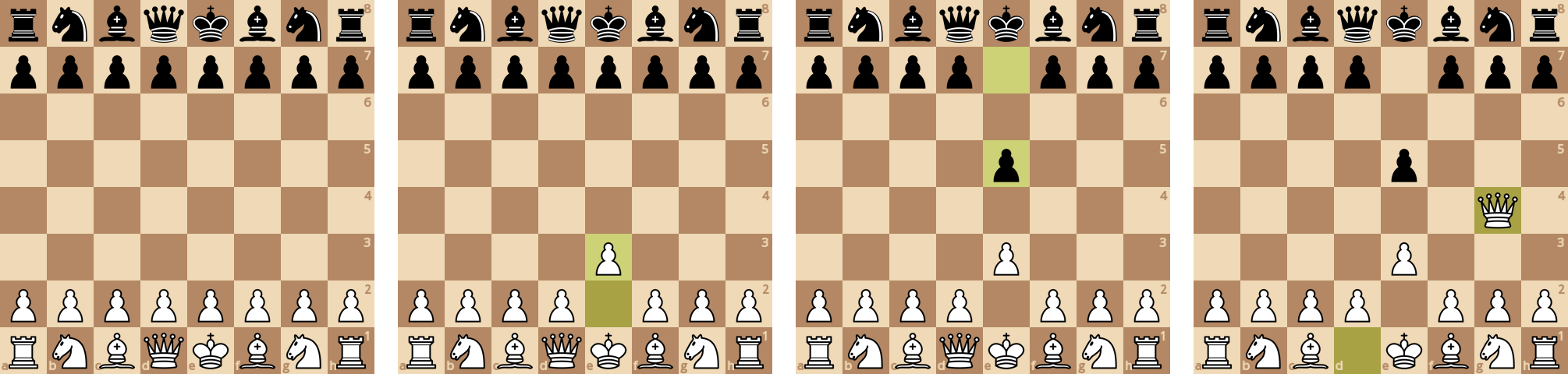
В стандартном дебюте белые выводят ферзя, потому что именно такой ход дает наибольший вклад в функцию оценки по параметру "мобильности". Так как в движке нет базы данных дебютов, то он не "знает" заведомо, что в шахматах так обычно не ходят.

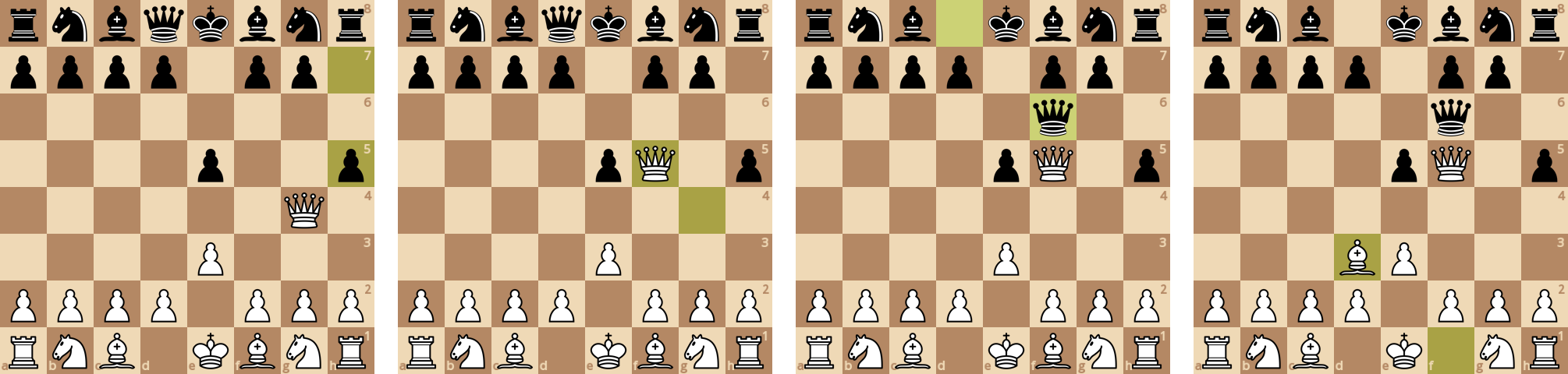
Черные также выводят ферзя, так как у них такая же оценка позиции.

После вывода фигур происходит размен ферзей.

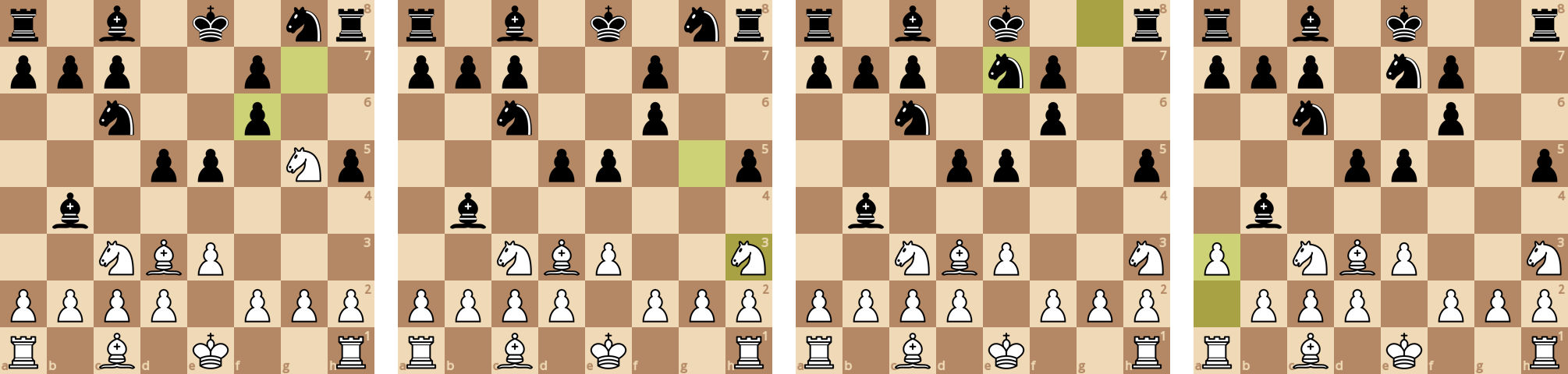
Далее партия развивается обычным образом. Пропустим несколько ходов...

В партиях иногда встречаются артефакты функции оценки - например, компьютер считает, что можно пожертвовать пешкой, чтобы разменять фигуры и уменьшить мобильность противника.

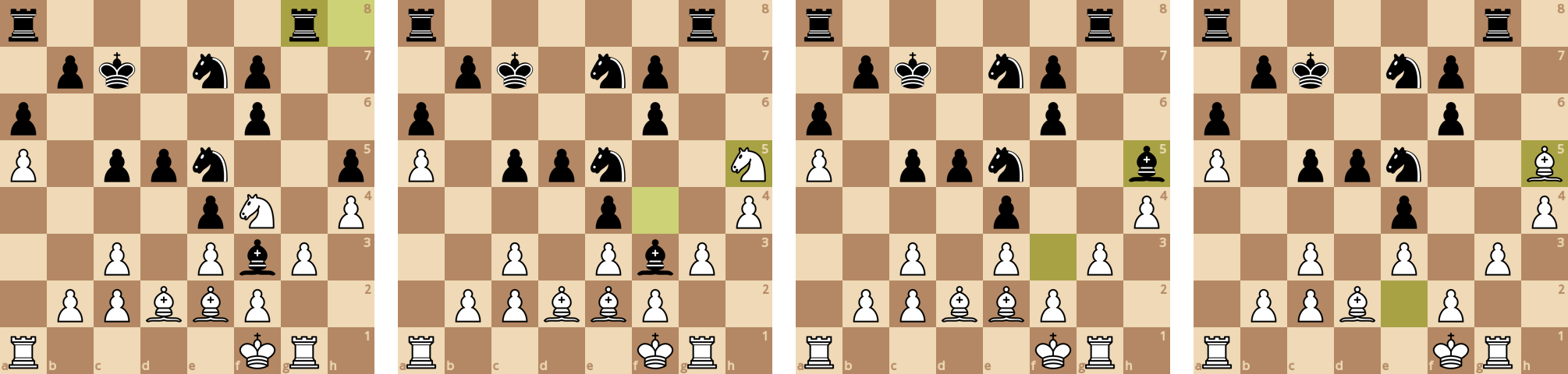
Стратегическое преимущество осталось за белыми. Ладья ходом на a4 создала угрозу - в будущем она может походить на f4 и создать "вилку", атакуя одновременно коня и пешку. Черные закрывают дорогу ладье ходом пешки на c4, но безрезультатно - белые разваливают остаток пешечного фронта и инициатива окончательно переходит к белым.

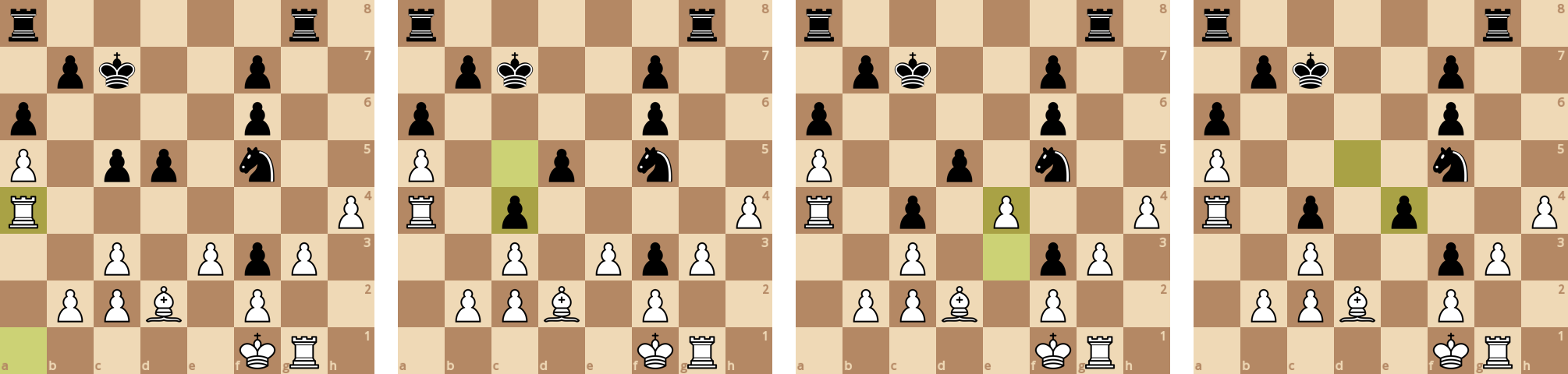
Черные отдают ладью, чтобы отсрочить поражение.

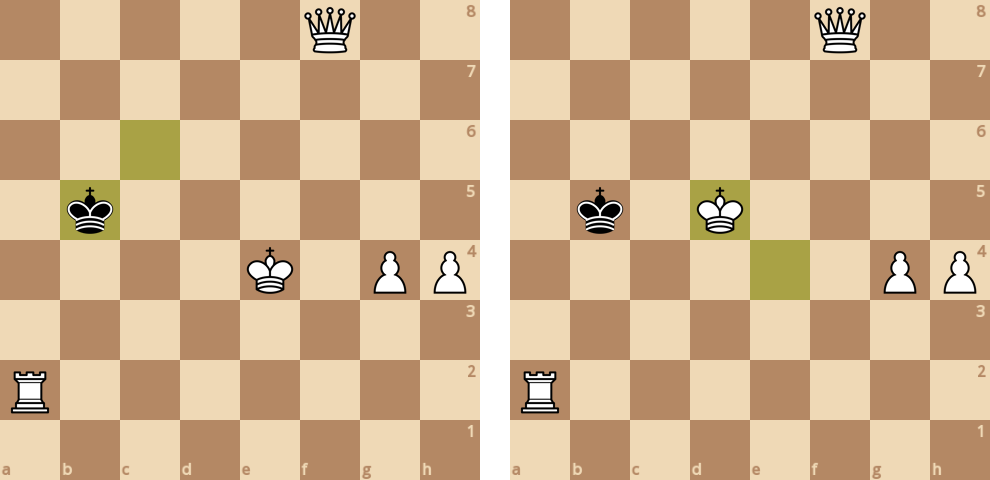
Черные предвидели мат и "сдали" партию, так как не нашли ни одного хода, где у них не съедают короля (мат в два хода: ♚b6 - ♕b8).

Эта партия состоит из 143 ходов, было проанализировано 18 355 708 досок, общее время расчета 92.3627 секунд (средняя скорость 198 735 досок/секунду).

Атака легкой кавалерии (Charge of The Light Brigade)

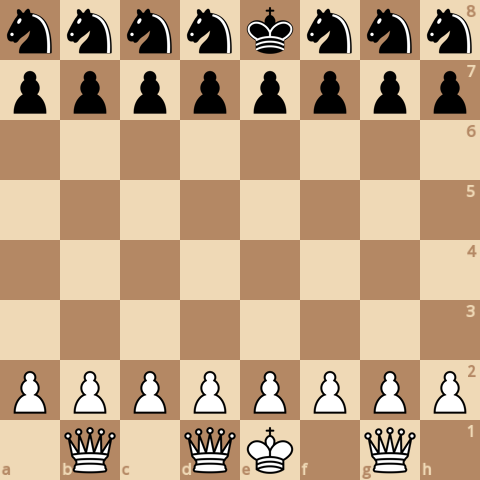
В этом варианте у белых есть 3 ферзя и 8 пешек, у черных есть 7 коней и 8 пешек. Автор этого варианта хотел показать, что не всегда "стоимость" позиции определяется ценностью фигур: если конь стоит 300 баллов, а ферзь 900 баллов, то у черных отставание в 600 баллов, но тем не менее у них превосходящая армия.

Посмотрим, правда ли, что конная кавалерия победит ферзей?

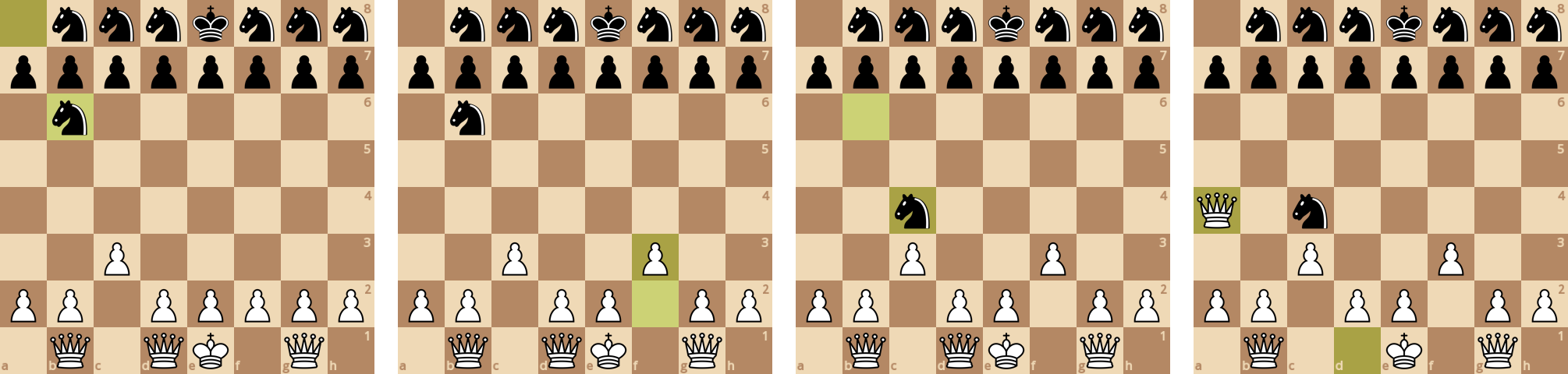
Белые пытаются сразу вывести ферзей, чтобы была лучшая мобильность. Это не очень хорошая тактика, потому что черные начинают выводить коней, одновременно с атаками на ферзей.

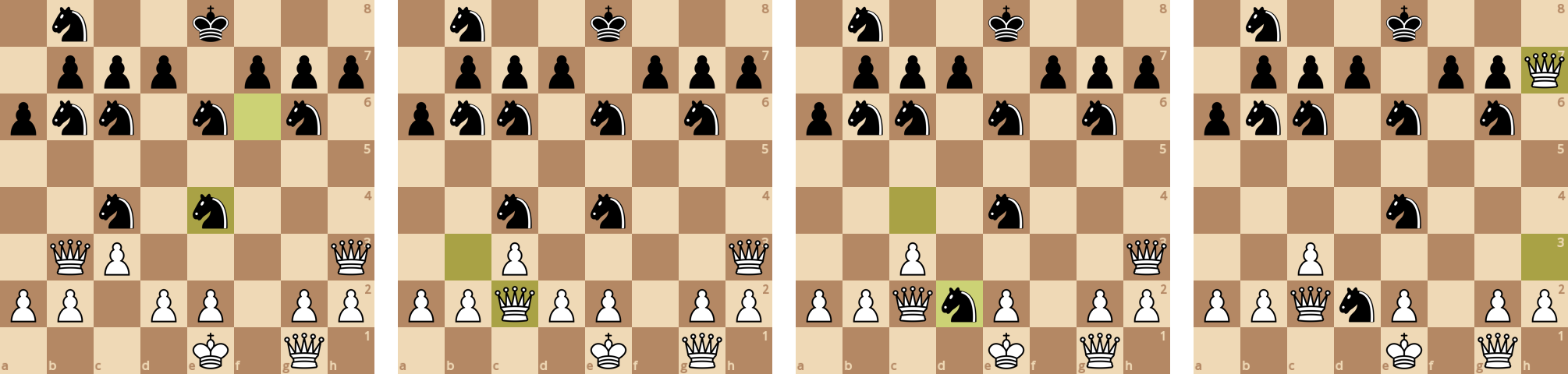
У черных намного более лучшая мобильность.

Белый ферзь берет коня на f4, чтобы избежать мгновенного мата (♞d3), но спустя пару шахов белые сдают партию, так как мат неизбежен (♔d3 - ♞c5).

Эта партия состоит из 89 ходов, было проанализировано 288 695 116 досок, общее время расчета 1467.55 секунд (средняя скорость 196 719 досок/секунду).

Орда (Horde)

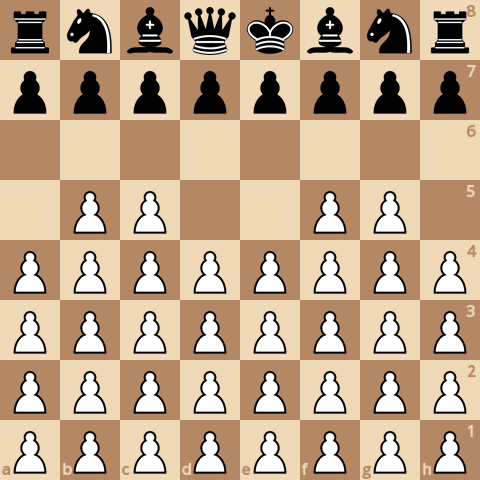
В этом варианте у белых 36 пешек. Черные для победы должны съесть все пешки. Этот вариант достаточно популярный, поддержан в многих онлайн-шахматах и про него даже есть книга.

Тактика для этого варианта заключается в том, что черным надо "освободить" какую-нибудь вертикаль, тогда все белые пешки будут съедены, так как они не имеют защиты "сзади".

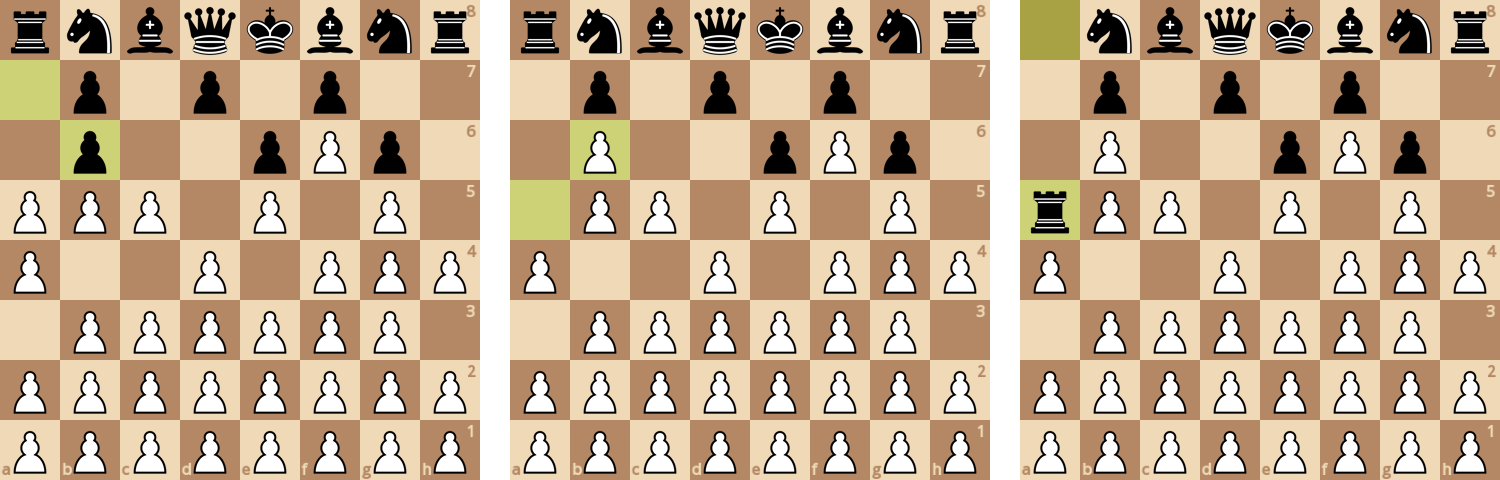
На склейке выше пример, как можно ломиться сквозь пешечную вертикаль.

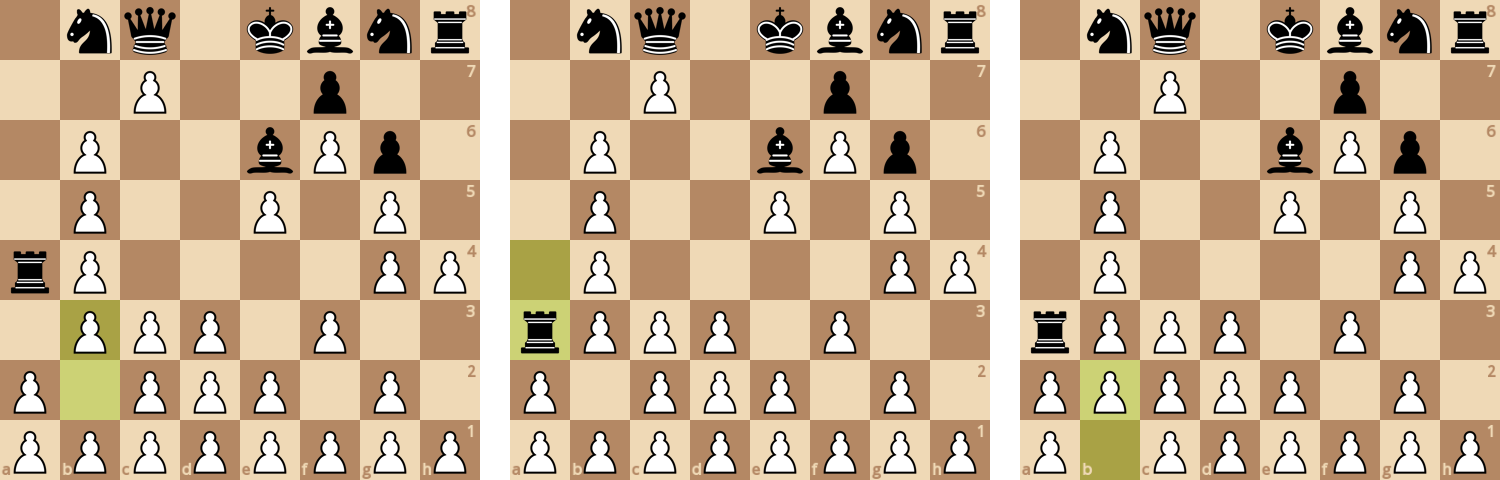
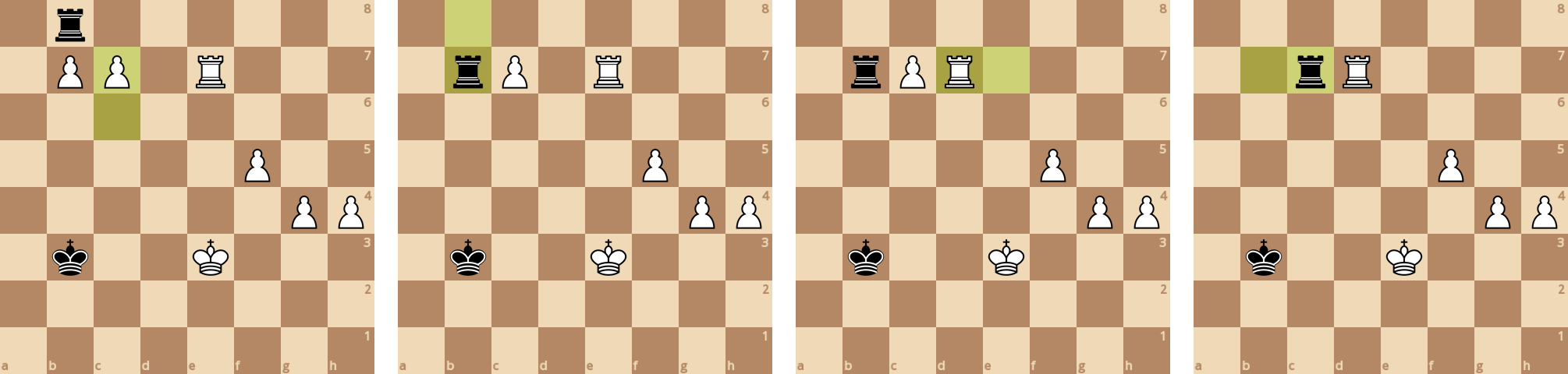
После 57 хода участь белых пешек предрешена - ладья теперь может съесть все пешки на первой горизонтали.

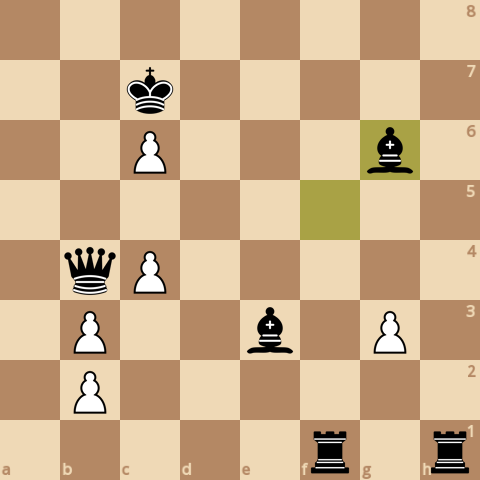
Эта партия состоит из 108 ходов, было проанализировано 128 196 318 досок, общее время расчета 672.735 секунд (средняя скорость 190 559 досок/секунду).

Крестьянское восстание (Peasants' Revolt)

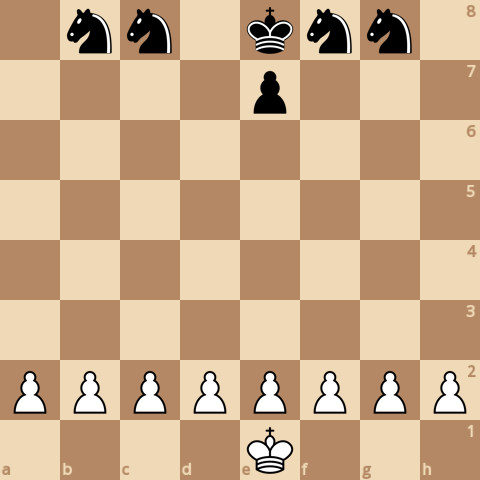
В этом варианте у белых есть только 8 пешек, у черных есть 1 пешка и 4 коня. У черных есть преимущество.

Так как дерево поиска очень маленькое, то можно было запускать полный перебор не только на 4 хода вперед, но и на 5 ходов, и на 6 ходов вперед. Во всех партиях белые проиграли.

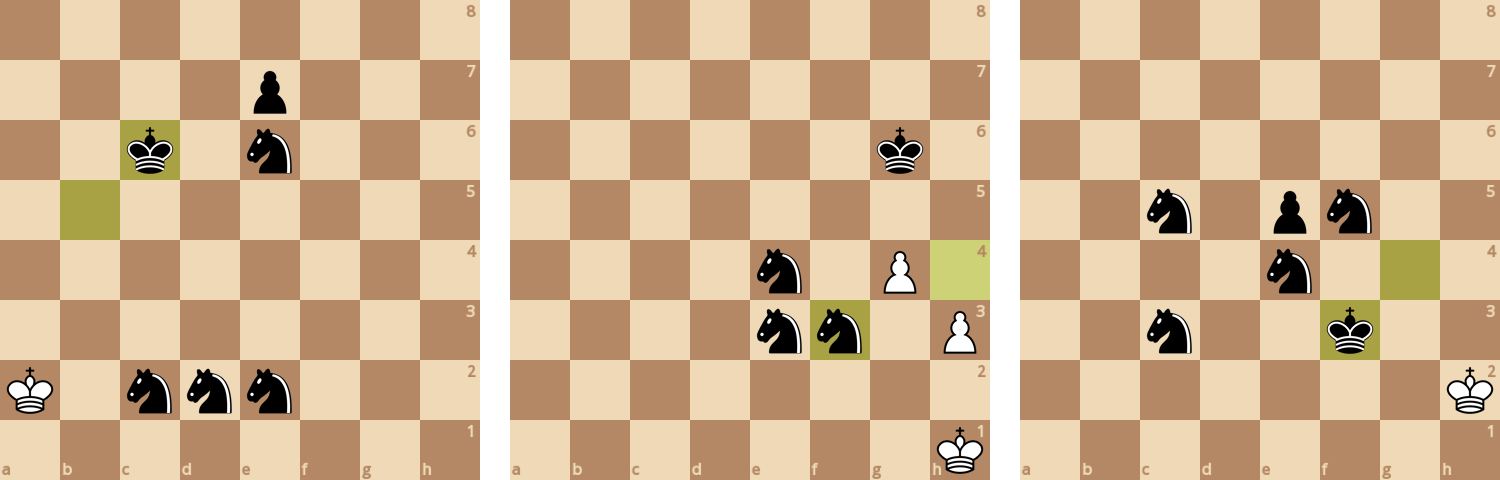
В переборе на 4 хода игра заняла 50 ходов, 2.64479 секунды на анализ (со скоростью 358 324 досок/секунду).

В переборе на 5 ходов игра заняла 56 ходов, 10.5065 секунды на анализ (со скоростью 376 271 досок/секунду).

В переборе на 6 ходов игра заняла 86 ходов, 371.099 секунды на анализ (со скоростью 334 532 досок/секунду).

Weak!

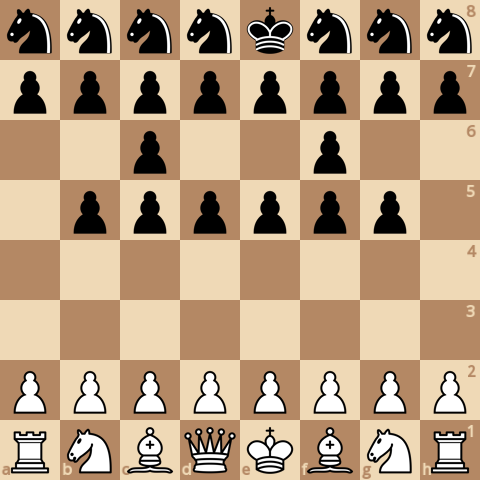
Это вариант средней интересности, с пешками и конями у черных.

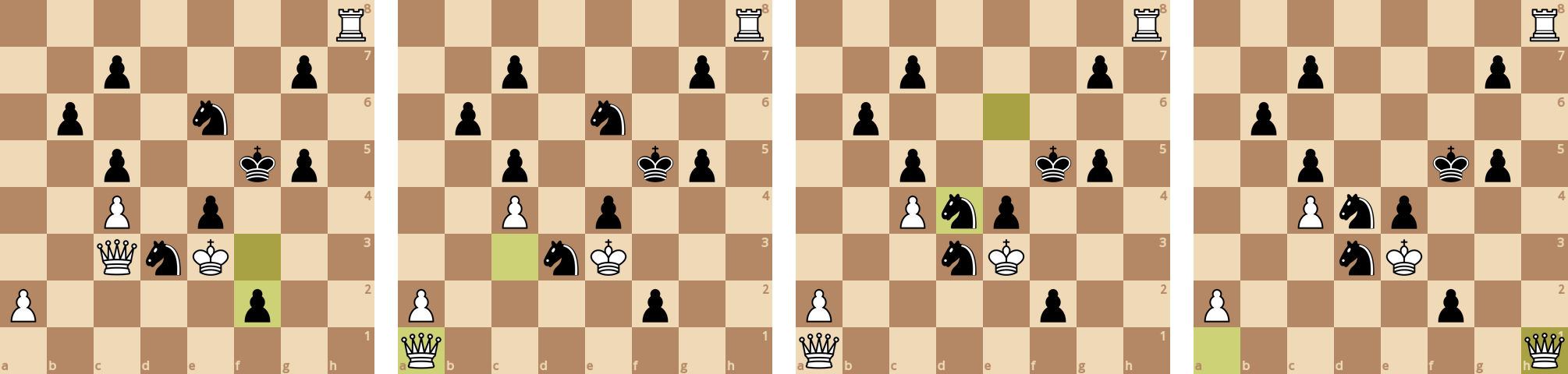
Черные разменяли коней на фигуры белых, но не смогли добиться выигрыша своими лишними пешками. Белые не попадали в "вилки" и не давали прохода черным пешкам.

Эта партия состоит из 143 ходов, было проанализировано 66 753 398 досок, общее время расчета 358.131 секунд (средняя скорость 186 393 досок/секунду).

Беролина (Berolina)

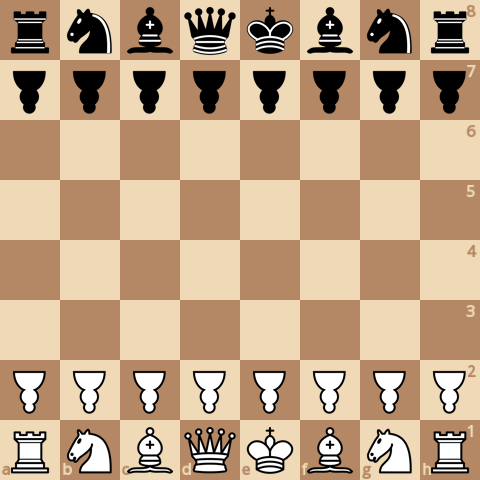
Теперь пора добавлять необычные фигуры. Шахматы Беролина - это вариант с "инвертированными пешками": пешки могут ходить только по диагонали (в любую сторону), а брать фигуры только по вертикали. Если пешка ходит в первый раз, она может походить на 2 диагонали вперед.

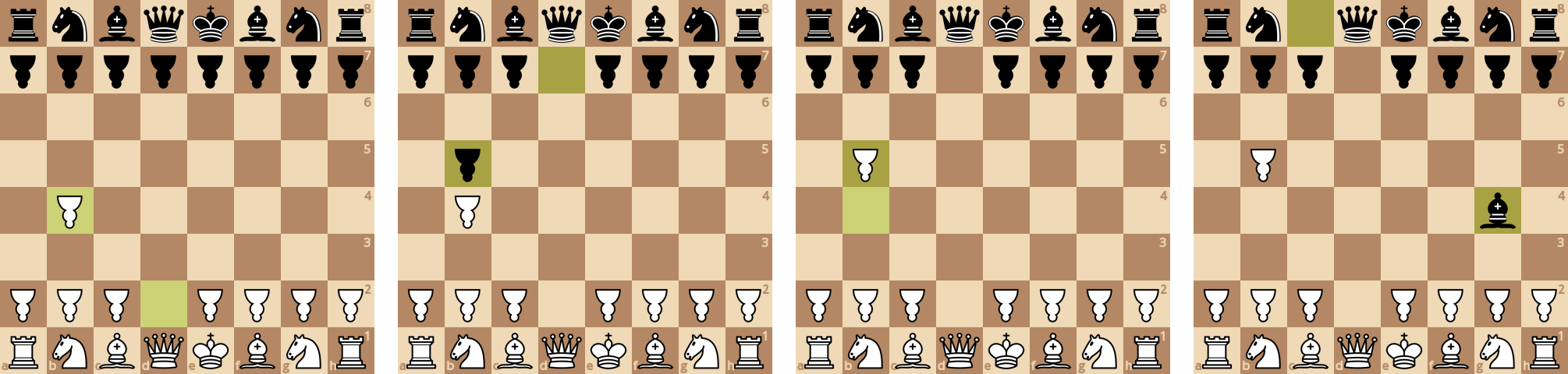
Стороны выводят свои ферзевые пешки.

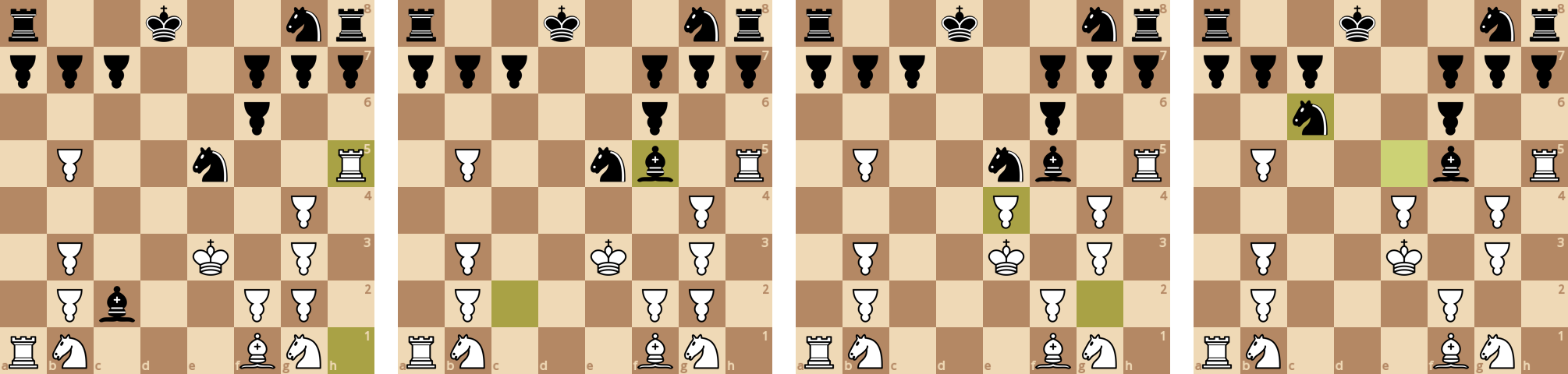
Белая ладья атакует незащищенного коня, слон закрывает ладье ход. Затем белая пешка опять атакует черного коня, и он отходит.

На склейке выше происходит необычный размен одной пешки и легкой фигуры - белая ладья становится немного мобильнее.

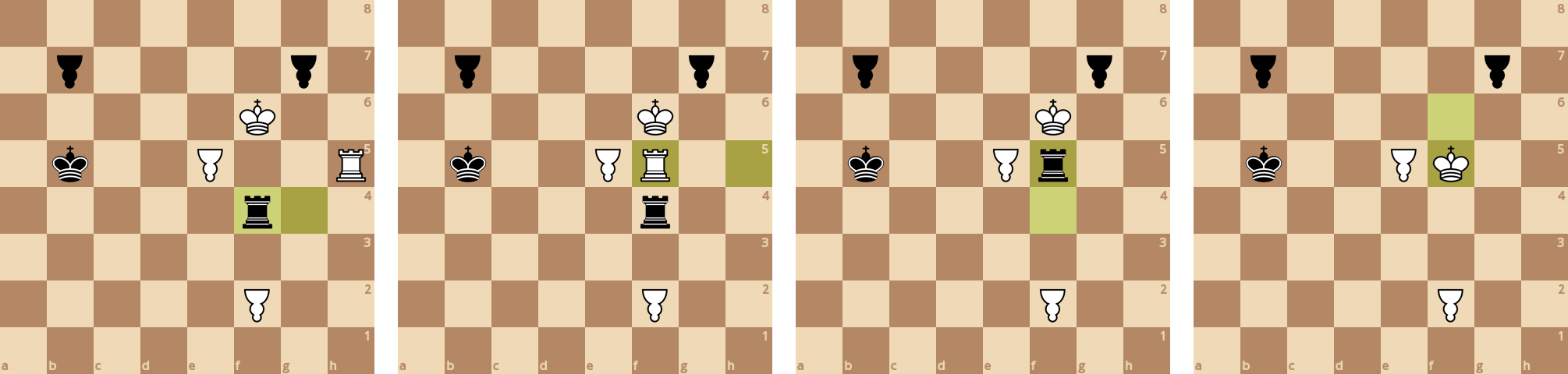
Белые выиграли партию - они смогли довести пешку до последней диагонали.

Игра довольно острая, можно посмотреть полную игру на github.

Эта партия состоит из 107 ходов, было проанализировано 101 661 065 досок, общее время расчета 571.838 секунд (средняя скорость 177 779 досок/секунду).

Бешеный король (Mad King)

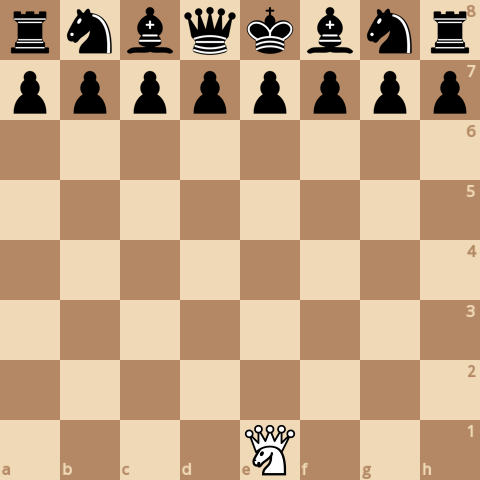
Вводится новая фигура - амазонка, она может ходить как ферзь и как конь. Эта фигура может поставить мат королю в одиночку. Вариант Mad King - у белых есть только одна амазонка, и надо поставить мат черным. Это "решенная" игра с выигрышом для черных, посмотрим что про это думает шахматный движок.

Черные гоняли амазонку по всей доске, не давая съесть ни одной фигуры. Единственное, чего добилась амазонка - съела пешку, но потом белые сдали партию, увидев неминуемое взятие амазонки.

Эта партия состоит из 54 ходов, было проанализировано 37 140 321 досок, общее время расчета 183.855 секунд (средняя скорость 202 008 досок/секунду).

Тутти-фрутти (Tutti-Frutti)

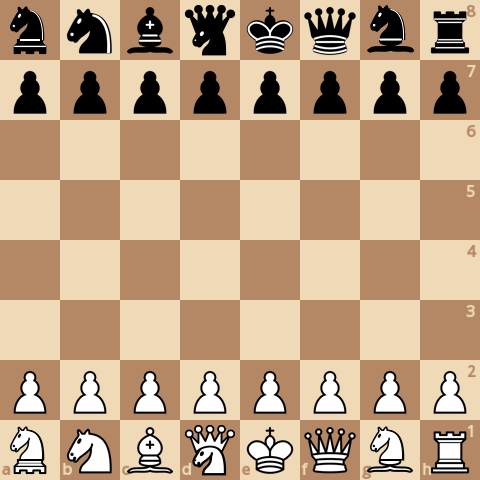
Тутти-фрутти это вариант с "усиленными" фигурами. Кроме амазонки, на доске стоят императрицы (ладья+конь) и принцессы (слон+конь).

Для новых фигур нужно определить их "стоимость". Я решил это так - если ладья стоит 500 баллов, слон стоит 300 баллов, ферзь (ладья+слон) стоит 900 баллов, то и императрица (ладья+конь) и принцесса (слон+конь) должны стоить 900 баллов. Амазонка (ладья+слон+конь) у меня стоит 1300 баллов.

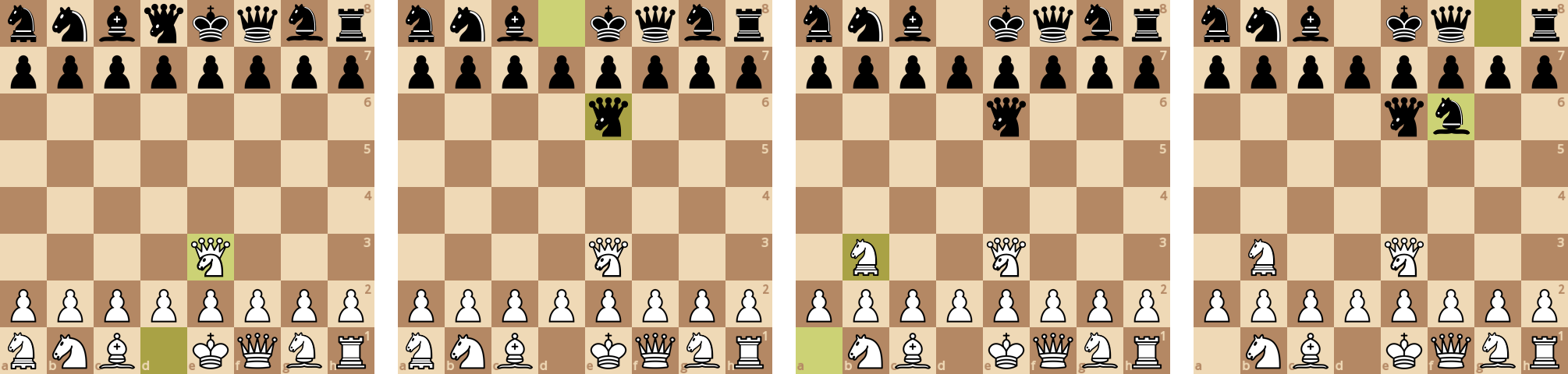
Игроки сразу выводят сильные фигуры.

Черные красиво отжимают ладью: их слон атаковал ферзя и одновременно позволил императрице сделать "вилку".

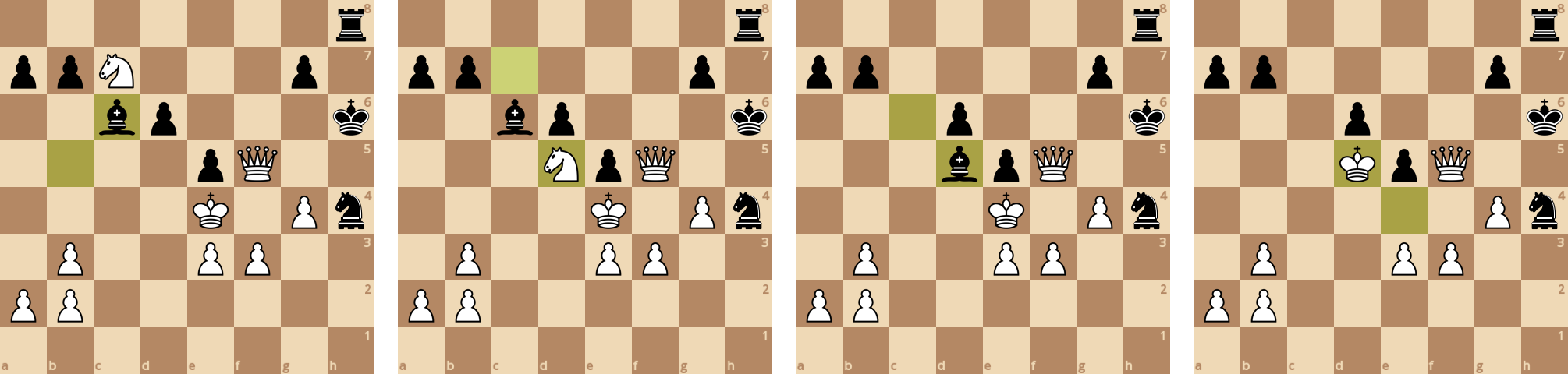
Черные заставили белых разменять фигуры, после чего с перевесом в ладью довели игру до своей победы.

Эта партия состоит из 120 ходов, было проанализировано 23 325 618 досок, общее время расчета 134.167 секунд (средняя скорость 173 855 досок/секунду).

Королевский конь (Knightmate)

В этом варианте конь и король меняются местами. Вместо двух коней есть две фигуры манн (от немецкого "Mann" - человек) - они двигаются как король, но являются обычными фигурами (могут быть съедены). Вместо короля есть королевский конь - он двигается как конь, но для победы ему нужно объявить мат. Я поставил "стоимость" манна в 150 баллов (как полторы пешки).

Здесь алгоритм очень крупно подставился - белые вывели королевского коня вперед, и черные стали выводить фигуры с помощью атаки на коня.

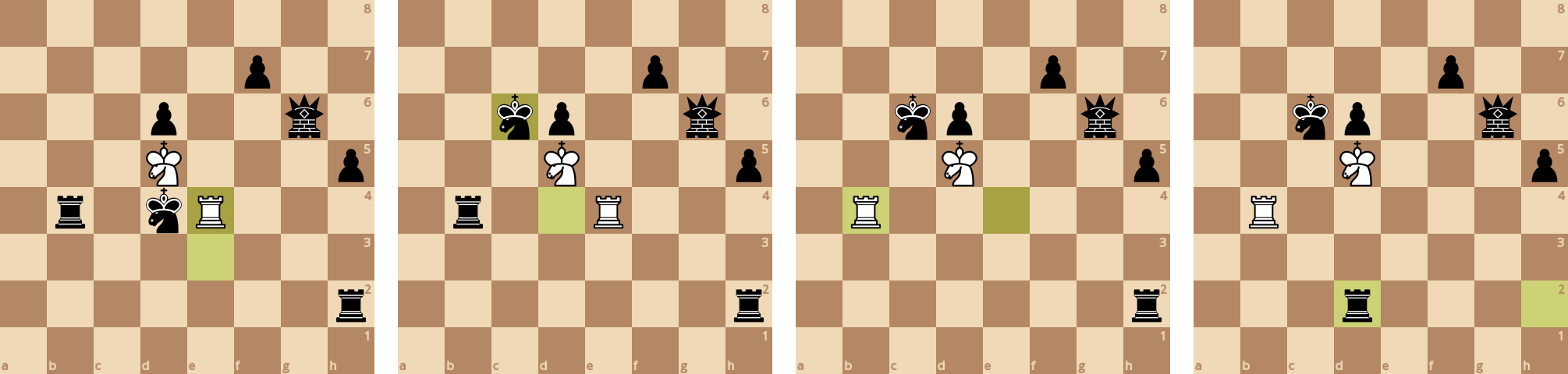
Белые забрали черную ладью, но не смогли защитить белую ладью - на 98 ходе черная ладья прогнала королевского коня. В итоге черные победили, загнав королевского коня в угол.

Эта партия состоит из 104 ходов, было проанализировано 20 463 291 досок, общее время расчета 119.934 секунд (средняя скорость 170 621 досок/секунду).

Попрыгунчик (Grasshopper)

У каждого игрока кроме стандартных фигур есть восемь попрыгунчиков (англ. grasshopper). Эти фигуры могут двигаться в любом направлении, но лишь "перепрыгивая" через другие фигуры (любого цвета).

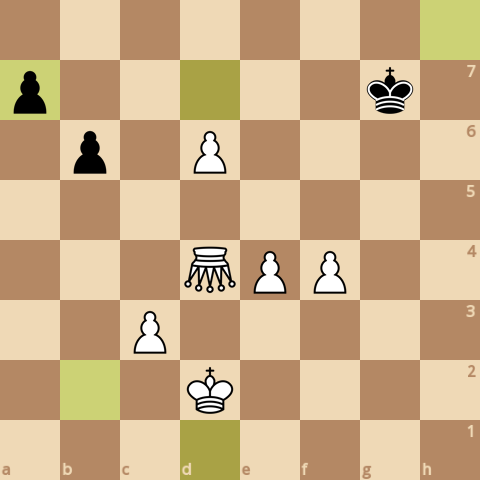
На изображении видны возможные ходы белого попрыгунчика - их 5 штук, в одном из ходов он может съесть черную пешку. Я поставил стоимость попрыгунчика в 200 баллов (как две пешки).

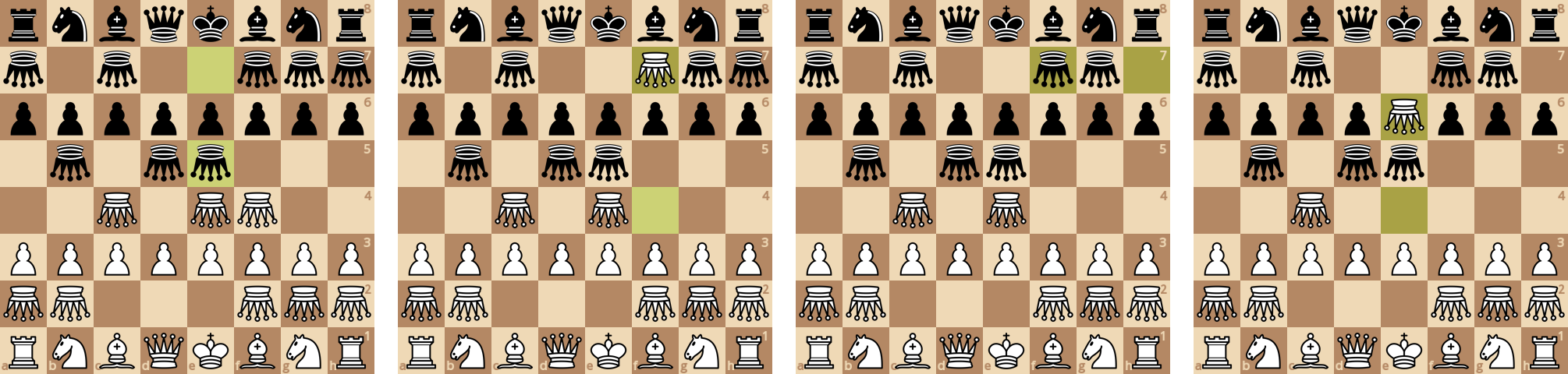
Попрыгунчики выводятся на доску и размениваются.

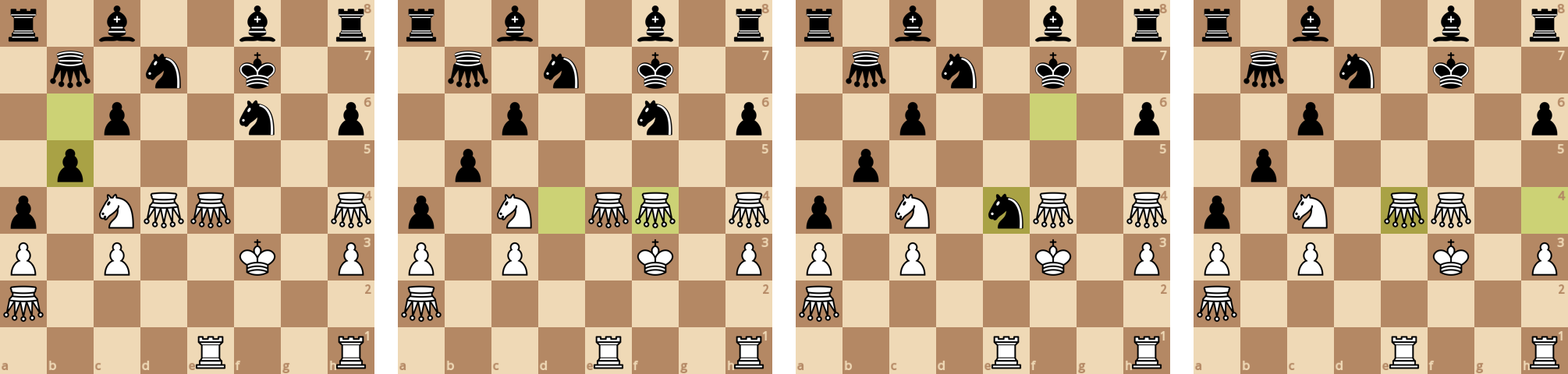
Белый попрыгунчик объявляет шах королю, от которого он избавляется ходом коня.

Белые понесли потери и им чуть не объявили мат - пришлось пожертвовать попрыгунчиком. На 120-м ходе белые сдали партию.

Эта партия состоит из 120 ходов, было проанализировано 116 240 217 досок, общее время расчета 963.316 секунд (средняя скорость 120 666 досок/секунду).

Атомные шахматы (Atomic)

Атомные шахматы - имеют стандартные правила, но при взятии какой-либо фигуры происходит "взрыв": атаковавшая фигура и все фигуры на соседних 8 клетках (независимо от цвета, и кроме пешек) убираются. По ссылке есть гифка, которая показывает это правило. Король тоже убирается, поэтому если взять фигуру рядом с ним, то противник выигрывает.

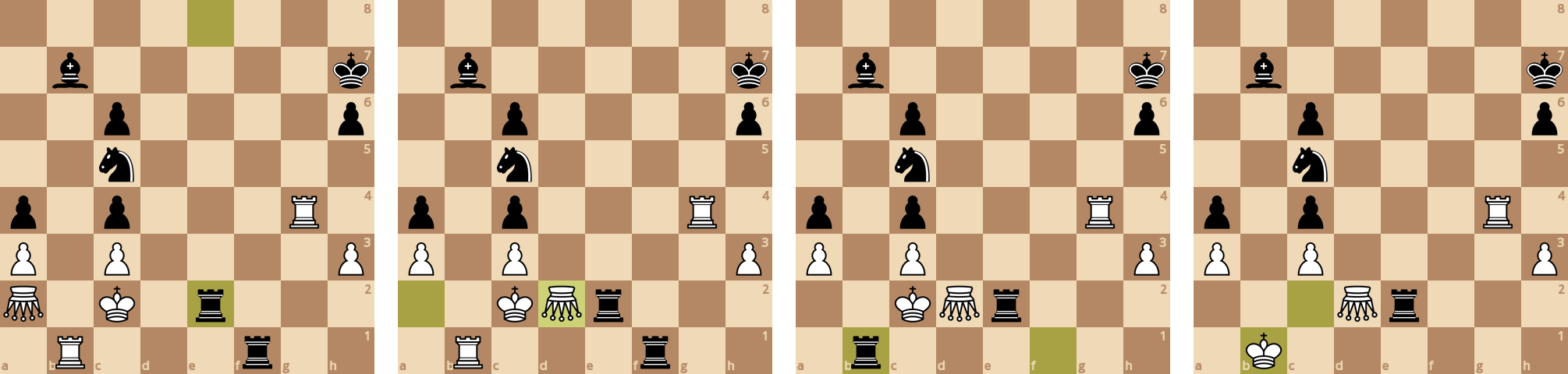
Партия сразу имеет острый характер. Уже на 3 ходу слон грозит взять пешку и взорвать короля, поэтому путь преграждается конем. То же самое делает ферзь, ход преграждается пешкой. Затем ферзь ходит ♕d5, и черные не могут его съесть, потому что этим взорвется черный конь, и белый слон в свою очередь взорвет короля, поэтому снова ход преграждается пешкой.

На склейке выше показан размен через взрывы в миттельшпиле. Обратите внимание - после 25 хода черная ладья может съесть белую, но это будет взаимное уничтожение и не поменяет баланс материала.

Игра довольно острая и стороны ходят очень осторожно. Единственные фигуры, которыми можно сравнительно безопасно играть - пешки, потому что взрывы на них не действуют. Кстати, король совершенно безоружен и никого съесть не может, потому что в таком случае он взорвется и автоматически проиграет.

Черные не могут спокойно съесть пешки из-за взрывов, поэтому белые без проблем проводят их вперед, а черные сдают партию на 90-м ходе.

Эта партия состоит из 90 ходов, было проанализировано 1 792 579 досок, общее время расчета 12.8841 секунд (средняя скорость 139 131 досок/секунду).

Так как дерево перебора меньше, то можно посмотреть на партию с полным перебором в 5 ходов на github, там ходят поумнее, но разбирать партию не буду, чтобы не раздувать статью.

Реализация атомных фигур сделана в шаблонном стиле без копипаста - atomic_pieces.h.

Шахматы Капабланки (Capablanca Chess)

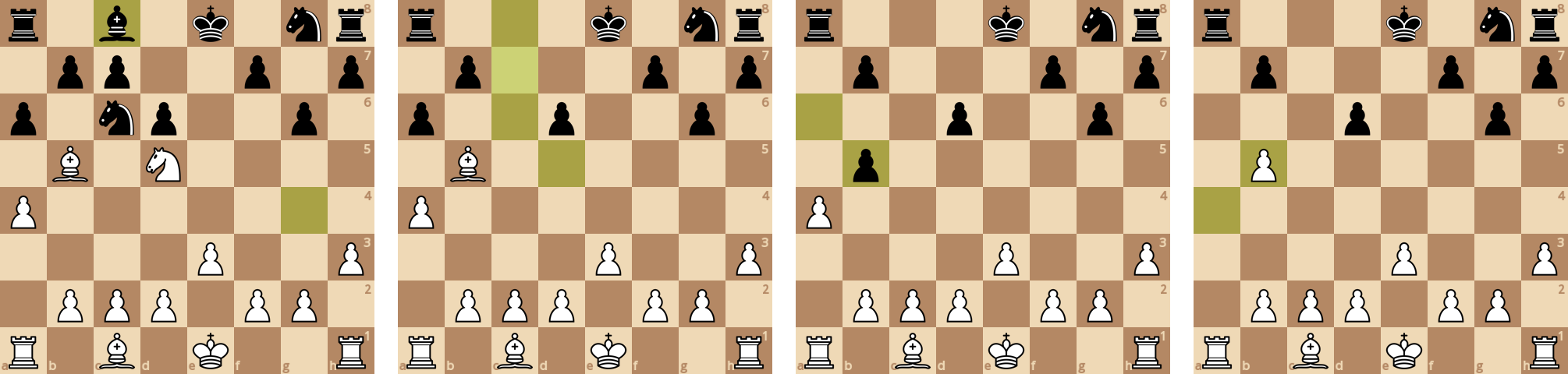
Настало время для шахмат с досками необычных размеров. Шахматы Капабланки - довольно известный вариант на доске 10x8 с уже знакомыми нам фигурами императрица и принцесса.

Игра идет в нормальном темпе, из заметок по варианту - ход пешками на вертикали d открывает угрозу для взятия пешек f2/f7.

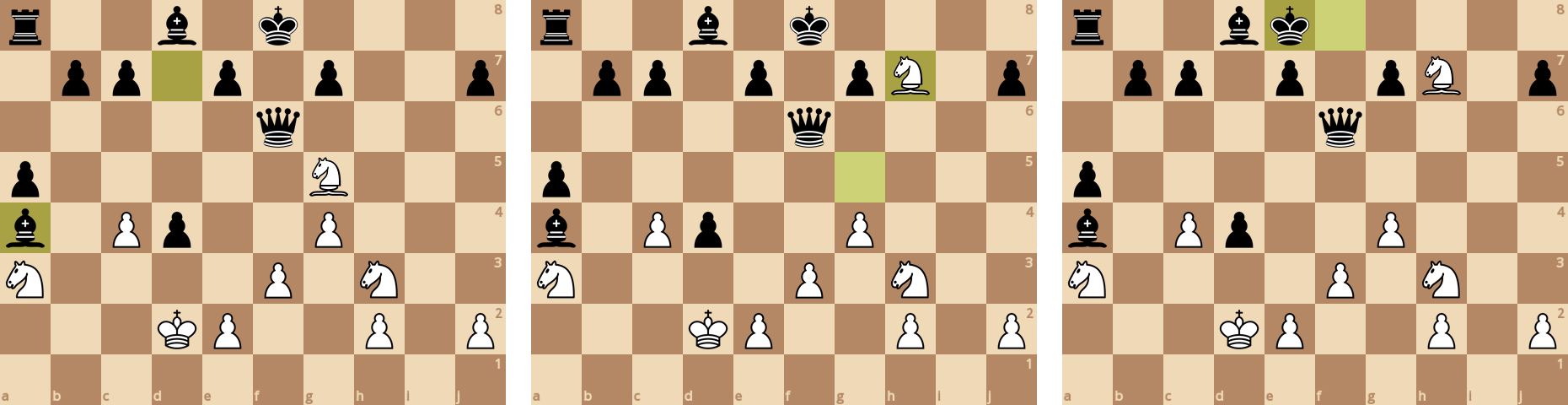
Белые проиграли ладью, и после размена все стало плохо. Белые сдали партию на 84 ходу.

Эта партия состоит из 84 ходов, было проанализировано 46 067 073 досок, общее время расчета 308.699 секунд (средняя скорость 149 229 досок/секунду).

Антилопа Гну (Wildebeest)

Wildebeest - это вариант средней интересности на доске 11x10. Там добавляются две фигуры, которые называются "верблюд" и "антилопа гну", но я не нашел для них иконки, поэтому у меня это две фигуры зебра и единорог.

Ходы зебры напоминают ходы коня, но "вектор" прыжков (3,1) вместо (2,1). Зебра ограничена одним цветом (как слон). Единорог может ходить как зебра и как конь. Я поставил стоимость зебры в 300 баллов, единорога в 600 баллов.

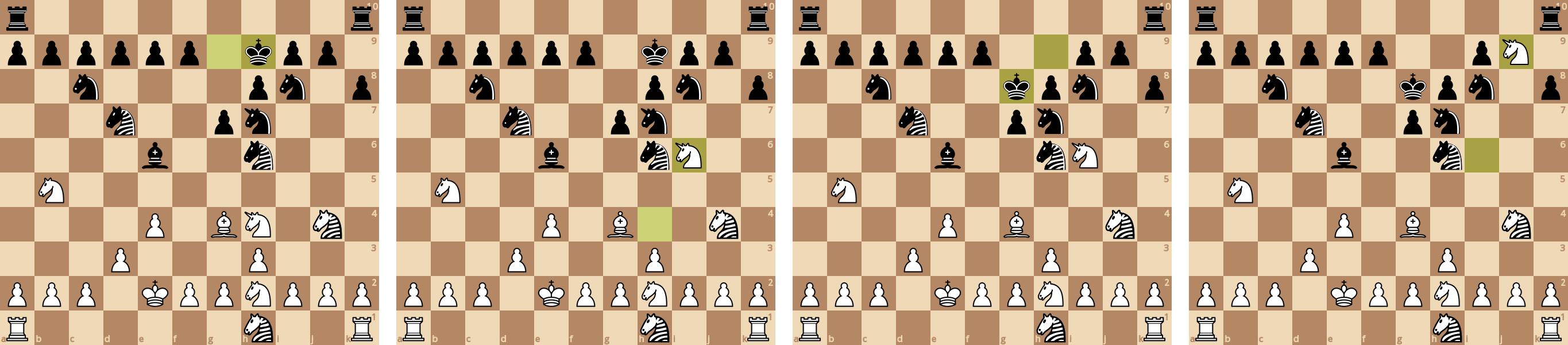
Белый единорог съедает пешку в миттельшпиле.

Каких-то интересных ходов не было, партия прошла вяло, белые постепенно проиграли. Эта партия состоит из целых 190 ходов, было проанализировано 235 850 073 досок, общее время расчета 2083.96 секунд (средняя скорость 113 173 досок/секунду).

Шахматы гарантированного возмездия (Stratomic)

Вариант Stratomic на доске 10x10 добавляет каждому игроку две ядерные ракеты. В игре есть "протокол эскалации" - ядерные ракеты можно запускать после того, как будет взята любая фигура кроме пешки. При запуске ядерной ракеты уничтожается сама ракета и все фигуры любого цвета, кроме короля, в выбранном игроком квадрате 3х3. Также ядерная ракета может ходить как король (чтобы обезопасить себя, если ее атакуют).

Размены не-пешечных фигур откладывались, но на 17 ходу произошла эскалация - был взят слон с шахом. После эскалации игроки обменялись ядерными ударами.

Так как я поставил стоимость ядерных ракет в 500 баллов, то, видимо, алгоритм посчитал неразумным тратить весь потенциал, и следующий ядерный удар произошел на 36 ходу.

Последний ядерный удар произошел на 45 ходу.

К эндшпилю у черных появилось преимущество - ладья против коня. Белые постепенно проиграли.

Эта партия состоит из 122 ходов, было проанализировано 113 019 048 досок, общее время расчета 2348.6 секунд (средняя скорость 48 121 досок/секунду).

Действительно большие шахматы (Really Big Board)

Действительно большие шахматы - вариант на доске 16x16. Пешки в первом ходе могут двигаться до 6 клеток вперед. Кроме рассмотренных ранее необычных фигур, добавилось еще четыре (названия мои): волшебник, чемпион, шут, дракон.

Волшебник ограничен своим цветом. Чемпион "протыкает" диагонали на две клетки. Шут называется так, потому что он бьёт не туда, куда "смотрит" (т.е. не по вертикали/горизонтали/диагонали). Стоимости фигур соответственно 300, 300, 500 баллов.

Дракон летает по "кругам" странным образом. Он может прилететь на исходное место, то есть игрок фактически может пропустить свой ход, если у него есть дракон. Стоимость дракона 500 баллов.

Вычисление на такой доске происходит в несколько раз медленнее, поэтому полный перебор был в 3 хода.

За мешаниной необычных фигур было довольно сложно следить за стратегией движка. Все закончилось внезапно, когда черные смогли объявить белым мат фактически в дебюте на 62 ходу.

Эта партия состоит из 62 ходов, было проанализировано 84 055 631 досок, общее время расчета 1969.06 секунд (средняя скорость 42 688 досок/секунду).