В этой статье я хочу рассказать о нашем собственном симуляторе, созданном для моделирования физики поездов в Assassin's Creed Syndicate. Действие игры происходит в Лондоне 1868 года, в период промышленной революции, когда развитие общества зависело от пара и стали. Для меня было огромным удовольствием поработать над уникальной возможностью реализации мира Лондона викторианской эпохи. Внимание к историческим и реальным деталям привело нас к созданию этой физической симуляции.
Введение
Сегодня писать свои физические движки не очень популярно. Однако бывают ситуации, в которых создание собственного физического симулятора с нуля чрезвычайно полезно. Такие ситуации могут возникать, когда есть особая необходимость в новой геймплейной функции или части симулируемого игрового мира. Именно такая проблема возникла у нас при разработке системы железных дорог и управления поездами в Лондоне 19-го столетия.
Стандартная система соединения европейских поездов приведена на Рис. 1 слева. Такая же система использовалась в поездах 19-го века в Лондоне [1]. Когда мы начали работу над поездами, то быстро осознали, что можно создать интересные взаимодействия и зависимости, симулируя стяжку физически. Поэтому вместо жёсткого скрепления вагонов мы соединили их подвижным сцепным устройством, управляющим движением всех вагонов поезда.
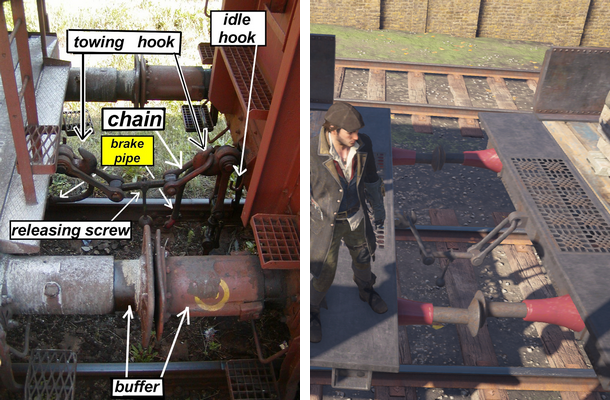
Рис. 1. Слева — детали винтовой стяжки (источник: Википедия [1]). Справа — соединительная система в Assassin’s Creed Syndicate.
В этом случае наша физическая симуляция даёт пару преимуществ:
- Извилистые железнодорожные пути проще контролировать с помощью 1D-симулятора. Принудительная вставка 3D-физики для использования ограничителей контроля за движением в одномерном пространстве — довольно рискованное решение. Она может быть очень чувствительна к возникающей нестабильности, из-за которой вагоны взлетят в воздух. Однако нам всё равно нужно было распознавать столкновения вагонов в полном 3D-пространстве.
- Подвижное соединение обеспечивает бóльшую свободу в дизайне геймплея. По сравнению с реальным миром, нам нужно гораздо большее расстояние между вагонами. Это требуется для того, чтобы иметь больше пространства для выполнения разных действий игрока и камеры (например, для взбирания на крышу вагона). Кроме того, наша стяжка соединена гораздо менее жёстко, чем в реальном мире, чтобы обеспечить более свободное относительное движение между вагонами. Это позволяет нам проще справляться с резкими поворотами железнодорожных путей, а распознавание столкновений между вагонами защищает от взаимопроникновения.
- Благодаря нашей системе мы можем выполнять расцепку вагонов (с учётом сил трения) и расчёт столкновений между отцепленными вагонами и остальной частью состава (например, при резкой остановке состава, когда отцепленные вагоны продолжают двигаться и в результате ударяются о состав).
Вот видео с примером работы нашей физики:
Мы начнём с раздела, в котором объясним, как контролируются поезда.
Примечание: чтобы упростить объяснения, мы обозначим термином «тягач» вагон, находящийся ближе к локомотиву, и термином «прицеп» вагон, расположенный ближе к хвосту поезда.
Управление локомотивом
Для управления локомотивом мы создали очень простой интерфейс, состоящий только из запросов требуемой скорости:
Locomotive::SetDesiredSpeed(float DesiredSpeed, float TimeToReachDesiredSpeed)Менеджер системы железных дорог отправляет такие запросы для каждого поезда, двигающегося в игре. Для выполнения запроса мы вычисляем силу, необходимую для создания требуемого ускорения. Мы используем следующую формулу (второй закон Ньютона):
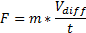
где F — вычисляемая сила, m — масса локомотива, 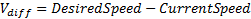 (требуемая скорость — текущая скорость), а t = TimeToReachDesiredSpeed (время для достижения требуемой скорости).
(требуемая скорость — текущая скорость), а t = TimeToReachDesiredSpeed (время для достижения требуемой скорости).
После вычисления силы мы передаём её в WagonPhysicsState как «силу двигателя» для приведения локомотива в движение (подробнее об этом в следующем разделе).
Поскольку физическое поведение поезда может зависеть, например, от количества вагонов (сталкивающиеся друг с другом вагоны создают цепную реакцию и толкают поезд вперёд), нам нужен способ обеспечить полное выполнение отправленного запроса требуемой скорости. Чтобы достичь этого, мы каждые 2 секунды повторно вычисляем скорость, необходимую для достижения требуемой скорости. Таким образом мы гарантируем, что отправленный запрос в результате будет выполнен. Но из-за этого мы не может точно соответствовать значению TimeToReachDesiredSpeed. Однако небольшие временны́е отклонения в игре приемлемы.
Кроме того, чтобы поддерживать скорость локомотива, заданную запросом SetDesiredSpeed, мы не позволяем ограничителю соединительной стяжки изменять скорость локомотива. Для компенсации отсутствия таких импульсов от ограничителей мы создали специальный метод для моделирования тяговой силы (подробнее о нём в разделе «Пуск поезда»). И, наконец, мы не позволяем реакции на столкновения изменять скорость локомотива, за исключением случая, когда поезд тормозит до нулевой скорости.
В следующем разделе описывается базовый уровень физической симуляции.
Шаг базовой симуляции
Вот структура, используемая для хранения физической информации о каждом вагоне (и локомотиве):
struct WagonPhysicsState
{
// Значения, изменяемые при интегрировании:
// расстояние вдоль путей и момент.
RailwayTrack m_Track;
float m_LinearMomentum;
// Скорость, вычисляемая из момента.
float m_LinearSpeed;
// Текущее значение сил.
float m_EngineForce;
float m_FrictionForce;
// Положение и поворот относительно мира, получаемые непосредственно от путей.
Vector m_WorldPosition;
Quaternion m_WorldRotation;
// Постоянная при симуляции:
float m_Mass;
}Как можно заметить, угловая скорость отсутствует. Даже если мы проверяем столкновения между вагонами с помощью 3D-коллайдеров (и поворот всегда соответствует направлению путей), поезда движутся в одномерном мире вдоль железнодорожных путей. Поэтому для физики не нужно хранить информацию об угловом движении. Кроме того, из-за одномерности симуляции, для хранения физических величин (сил, моментов и скорости) достаточно переменных типа float.
Для каждого вагона в качестве шага базовой симуляции мы используем метод Эйлера [2] (dt — это время одного шага симуляции):
void WagonPhysicsState::BasicSimulationStep(float dt)
{
// Вычисление производных.
float dPosition = m_LinearSpeed;
float dLinearMomentum = m_EngineForce + m_FrictionForce;
// Обновление момента.
m_LinearMomentum += dLinearMomentum*dt;
m_LinearSpeed = m_LinearMomentum / m_Mass;
// Обновление положения.
float DistanceToTravelDuringThisStep = dPosition*dt;
m_Track.MoveAlongSpline( DistanceToTravelDuringThisStep );
// Получение нового положения и поворота от путей.
m_WorldPosition = m_Track.GetCurrentWorldPosition();
m_WorldRotation = m_Track.AlignToSpline();
}Для реализации BasicSimulationStep мы используем три основных уравнения. Эти уравнения показывают, что скорость — это производная от положения, а сила — производная момента (точка над символом обозначает производную по времени) [2 — 4]:
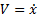
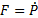
В третьем уравнении определяется момент P, являющийся произведением массы и скорости:
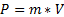
В нашей реализации приложение импульса к вагону является просто операцией суммирования с текущим моментом:
void WagonPhysicsState::ApplyImpulse(float AmountOfImpulse)
{
m_LinearMomentum += AmountOfImpulse;
m_LinearSpeed = m_LinearMomentum / m_Mass;
}Как можно увидеть, сразу после изменения момента мы пересчитываем скорость для более удобного доступа к этому значению. Это делается так же, как в [2].
Теперь, имея базовый метод расчётов изменений со временем, мы можем перейти к другим частям алгоритма.
Высокоуровневые шаги симуляции для одного поезда
Вот псевдокод полного шага симуляции для одного поезда:
// Часть А
Обновление скоростей пуска поезда
// Часть Б
Для всех вагонов поезда
ApplyDeferredImpulses (Приложение полученных импульсов)
// Часть В
Для всех вагонов поезда
UpdateCouplingChainConstraint (Обновление ограничителя соединительной стяжки)
// Часть Г
Для всех вагонов поезда
UpdateEngineAndFrictionForces (Обновление сил двигателя и трения)
SimulationStepWithFindCollision (Шаг симуляции и поиск столкновений)
CollisionResponse (Реакция на столкновение)Важно упомянуть, что, как и написано в псевдокоде, каждая часть выполняется последовательно для всех вагонов одного поезда. В части А реализуется особое поведение, связанное с пуском поезда. В части Б прикладываются импульсы, полученные при столкновениях. Часть В — это алгоритм решения для соединительной стяжки, гарантирующий, что мы не превысили максимальное расстояние для стяжки. Часть Г отвечает за силы двигателя и трения, шаг базовой симуляции (интегрирование) и обработку коллизий.
В алгоритме симуляции всегда сохраняется тот же порядок обновлений для вагонов поезда. Мы начинаем с локомотива и последовательно проходим по всем вагонам поезда, с первого до последнего. Поскольку мы можем использовать это свойство в симуляторе, оно упрощает формулировку вычислений. Мы используем эту характеристику только для контакта столкновений, для последовательной симуляции движения каждого вагона и проверки столкновения только с одним соседним вагоном.
Каждая часть этого цикла высокоуровневой симуляции подробно рассмотрена в последующих разделах. Из-за особой важности части Г мы начнём с неё и с SimulationStepWithFindCollision.
Симуляция со столкновениями
Вот код функции SimulationStepWithFindCollision:
WagonPhysicsState SimulationStepWithFindCollision(WagonPhysicsState InitialState, float dt)
{
WagonPhysicsState NewState = InitialState;
NewState.BasicSimulationStep( dt );
bool IsCollision = IsCollisionWithWagonAheadOrBehind( NewState );
if (!IsCollision)
{
return NewState;
}
return FindCollision(InitialState, dt);
}Сначала мы выполняем пробный шаг симуляции с полным изменением времени, вызывая
NewState.BasicSimulationStep( dt );и проверяя, обнаруживаются ли в новом состоянии какие-нибудь столкновения:
bool IsCollision = IsCollisionWithWagonAheadOrBehind( NewState );Если этот метод возвращает false, то можно использовать непосредственно новое вычисленное состояние. Но если обнаружено столкновение, мы выполняем FindCollision для нахождения более точного времени и состояния физики прямо перед событием столкновения. Для выполнения этой задачи мы применяем бинарный поиск, похожий на использованный в [2].
Вот цикл для нахождения более точного времени столкновения и состояния физики:
WagonPhysicsState FindCollision(WagonPhysicsState CurrentPhysicsState, float TimeToSimulate)
{
WagonPhysicsState Result = CurrentPhysicsState;
float MinTime = 0.0f;
float MaxTime = TimeToSimulate;
for (int step = 0 ; step<MAX_STEPS ; ++step)
{
float TestedTime = (MinTime + MaxTime) * 0.5f;
WagonPhysicsState TestedPhysicsState = CurrentPhysicsState;
TestedPhysicsState.BasicSimulationStep(TestedTime);
if (IsCollisionWithWagonAheadOrBehind(TestedPhysicsState))
{
MaxTime = TestedTime;
}
else
{
MinTime = TestedTime;
Result = TestedPhysicsState;
}
}
return Result;
}Каждая итерация всё больше приближает нас к точному времени столкновения. Мы также знаем, что нужно проверять столкновение только с одним вагоном, находящимся прямо перед текущим (или за ним, в случае движения назад). Для расчёта результата метод IsCollisionWithWagonAheadOrBehind использует проверку столкновения между двумя ориентированными коллайдерами (oriented bounding boxes, OBB). Мы проверяем столкновения в полном 3D-пространстве с помощью m_WorldPosition и m_WorldRotation из WagonPhysicsState.
Реакция на столкновение
Получив состояние физики прямо перед событием столкновения, мы должны вычислить соответствующий реактивный импульс j, чтобы приложить его и к тягачу (tractor), и к прицепу (trailer). Мы начнём с вычисления для текущей относительной скорости между вагонами перед столкновением:
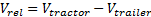
Схожее значение относительной скорости 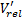 , после события столкновения:
, после события столкновения:
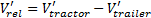
где 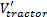 и
и 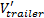 — скорости после приложения импульса реакции на столкновение j. Эти скорости можно вычислить с помощью скоростей до столкновения и импульса j следующим образом (
— скорости после приложения импульса реакции на столкновение j. Эти скорости можно вычислить с помощью скоростей до столкновения и импульса j следующим образом (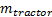 и
и 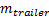 — это массы вагонов):
— это массы вагонов):
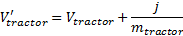
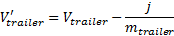
Теперь мы готовы определить коэффициент упругого восстановления r:
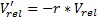
Коэффициент упругого восстановления определяет, насколько «упруга» реакция на столкновение. Значение r = 0 означает полную потерю энергии, значение r = 1 — отсутствие потери энергии (абсолютную упругость). Подставляя это уравнение в предыдущие формулы, получаем
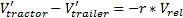
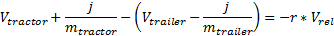
Упорядочим это уравнение, чтобы получить импульс j:
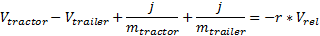
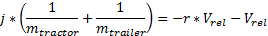
Наконец, мы можем вычислить импульс j:
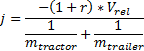
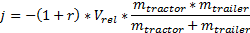
В игре мы используем коэффициент упругого восстановления r = 0.35.
Прикладываем импульс +j к тягачу и импульс -j к прицепу. Однако для тягача мы используем «отложенные» импульсы. Поскольку мы уже выполнили интегрирование для тягача и не хотим изменять его текущую скорость, то откладываем импульс на следующий кадр симуляции. Визуально это не очень заметно, потому что разница в один кадр мало видна. Такой «отложенный» импульс сохраняется для вагона и применяется в части Б следующего кадра симуляции.
Видео с примером остановки поезда:
Соединительная стяжка (цепь)
Можно воспринимать соединительную стяжку как ограничитель расстояния между вагонами. Чтобы удовлетворять требованию этого ограничителя расстояния, мы вычисляем и прикладываем соответствующие импульсы для изменения скоростей.
Мы начинаем вычисления с уравнения расстояния для следующего шага симуляции. Для каждых двух вагонов, соединённых стяжкой, мы вычисляем расстояния, которые они пройдут в течение ближайшего шага симуляции. Мы очень просто можем вычислить такое расстояние с помощью текущей скорости (и исследуя интегральные уравнения):

где x — расстояние, V — текущая скорость, а t — время шага симуляции.
Затем мы вычисляем формулу:
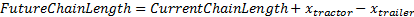
где:
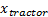 — расстояние, которое пройдёт тягач на ближайшем шаге симуляции.
— расстояние, которое пройдёт тягач на ближайшем шаге симуляции.
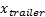 — расстояние, которое пройдёт прицеп на ближайшем шаге симуляции.
— расстояние, которое пройдёт прицеп на ближайшем шаге симуляции.
Если FutureChainLength больше максимальной длины соединительной стяжки, то ограничитель расстояния на следующем шаге симуляции будет разорван. Примем, что
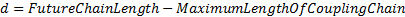
Если ограничитель расстояния будет разорван, то значение d будет положительным. В таком случае, чтобы удовлетворять условию ограничителя расстояния, нам нужно приложить такие импульсы, чтобы d = 0. Чтобы установить масштаб необходимых импульсов, используем массу вагона. Нужно, чтобы более лёгкий вагон двигался больше, а более тяжёлый — меньше. Назначим следующие коэффициенты 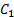 и
и 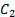
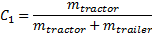
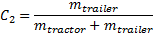
Заметьте, что 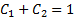 . Нам нужно, чтобы на следующем шаге симуляции прицеп прошёл с дополнительным расстоянием
. Нам нужно, чтобы на следующем шаге симуляции прицеп прошёл с дополнительным расстоянием 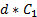 , а тягач — с расстоянием
, а тягач — с расстоянием 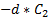 . Чтобы выполнить это приложением импульса, нам нужно умножить данное расстояние на массу, поделённую на время шага симуляции:
. Чтобы выполнить это приложением импульса, нам нужно умножить данное расстояние на массу, поделённую на время шага симуляции:
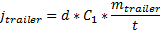
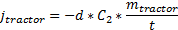
Если использовать следующий дополнительный коэффициент C
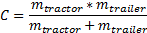
то можно упростить формулы импульсов до
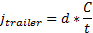

Можно заметить, что они имеют одинаковую величину, но разные знаки.
После приложения обоих импульсов вагоны, соединённые такой соединительной стяжкой, не разорвут ограничитель расстояния на следующем шаге симуляции. Эти импульсы изменяют скорости таким образом, что в результате в формулах интегрирования получаются положения, удовлетворяющие условию максимального расстояния для стяжки.
Однако даже после вычисления этих импульсов для одной соединительной стяжки существует вероятность разрыва максимального расстояния стяжки для других вагонов в поезде. Нам нужно будет несколько раз выполнить этот метод для сведения к конечному результату. Однако на практике выяснилось, что достаточно всего одного цикла. Его хватает для получения удовлетворительных общих результатов.
Мы выполняем эти вычисления последовательно для каждой соединительной стяжки в поезде, начиная с локомотива. Мы всегда прикладываем импульсы к обоим вагонам, соединённым стяжкой. Но в этом правиле есть одно исключение: мы никогда не прикладываем импульс к локомотиву. Нам нужно, чтобы локомотив сохранял свою скорость, поэтому импульс прикладывается только к первому вагону после локомотива. Этот импульс прикладывается только к прицепу, которому необходима компенсация для всего требуемого расстояния d (в таком случае имеем 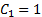 ,
, 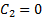 и
и 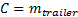 ).
).
Коррекция при резких поворотах
Поскольку симуляция выполняется вдоль одномерной линии, у нас возникают проблемы с идеальным соответствием для соединительной стяжки на крюке, когда вагоны двигаются на резких поворотах. В этой ситуации 1D-мир пересекается с 3D-миром игры. Соединительная стяжка располагается в 3D-мире, но импульсы (компенсирующие для удовлетворения условия ограничителя расстояния) прикладываются только в упрощённом 1D-мире. Для коррекции определения окончательного положения стяжки на крюке мы немного изменяем MaximumLengthOfCouplingChain в зависимости от относительного угла между направлениями тягача и стяжки. Чем больше угол, тем меньше максимально возможная длина стяжки. Сначала мы вычисляем скалярное произведение двух нормализованных векторов:
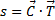
где 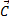 — нормализованное направление соединительной стяжки, а
— нормализованное направление соединительной стяжки, а 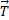 — вектор направления вперёд тягача. Затем мы используем следующую формулу для окончательного вычисления расстояния, которое нужно вычесть из физической длины соединительной стяжки:
— вектор направления вперёд тягача. Затем мы используем следующую формулу для окончательного вычисления расстояния, которое нужно вычесть из физической длины соединительной стяжки:
float DistanceConvertedFromCosAngle = 2.0f*clamp( (1.0f-s)-0.001f, 0.0f, 1.0f );
float DistanceSubtract = clamp( DistanceConvertedFromCosAngle, 0.0f, 0.9f );Как вы видите, мы не вычисляем точное значение угла, а используем непосредственно косинус. Это экономит нам немного вычислительного времени и этого достаточно для наших потребностей. Также можно использовать дополнительные числа на основании эмпирических тестов, чтобы ограничить значения в допустимых пределах. И, наконец, мы используем значение DistanceSubtract, чтобы удовлетворять условию ограничителя длины для соединительной стяжки:
MaximumLengthOfCouplingChain = ChainPhysicalLength - DistanceSubtract;Оказалось, что на практике эти формулы работают очень хорошо. Они обеспечивают правильное свешивание соединительной стяжки на крюке даже на резких поворотах маршрута путей.
Теперь мы рассмотрим особый случай — пуск поезда.
Пуск поезда
Как я упомянул ранее, мы не позволяем импульсам соединительной стяжки менять скорость локомотива. Однако нам всё равно нужен способ симуляции эффектов тяговой силы, особенно при пуске поезда. Когда локомотив запускается, он начинает тянуть другие вагоны, однако сам локомотив тоже должен замедляться соответственно массе вагонов. Чтобы достичь этого, мы изменяем скорости, когда поезд ускоряется с нулевой скорости. Мы начинаем с вычислений, основанных на законе уравновешивания момента. Этот закон гласит, что «момент системы постоянен, если на систему не действуют внешние силы» [3]. Это значит, что в нашем случае момент 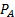 перед началом буксировки другого вагона должен быть равен моменту
перед началом буксировки другого вагона должен быть равен моменту 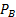 сразу после того, как соединительная стяжка потянет другой вагон:
сразу после того, как соединительная стяжка потянет другой вагон:
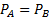
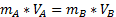
В нашем случае можно развернуть это до следующей формулы:
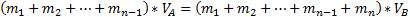
где 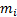 — масса i-того вагона (
— масса i-того вагона (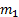 — масса локомотива),
— масса локомотива), 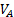 — текущая скорость локомотива (мы принимаем, что все уже движущиеся вагоны имеют одинаковую с локомотивом скорость),
— текущая скорость локомотива (мы принимаем, что все уже движущиеся вагоны имеют одинаковую с локомотивом скорость), 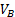 — скорость системы после буксирования (принимаем, что все буксируемые вагоны имеют одинаковую скорость). Если использовать дополнительное обозначение
— скорость системы после буксирования (принимаем, что все буксируемые вагоны имеют одинаковую скорость). Если использовать дополнительное обозначение 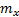 , определяемое как
, определяемое как
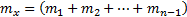
то можно упростить формулу следующим образом
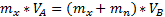
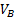 — это значение, которое мы ищем:
— это значение, которое мы ищем:
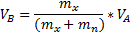
С помощью этой формулы можно просто установить новую скорость 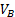 для локомотива и всех вагонов (от 2 до n), которые в данный момент тянутся соединительной стяжкой.
для локомотива и всех вагонов (от 2 до n), которые в данный момент тянутся соединительной стяжкой.
На Рис. 2 показано схематическое описание момента, когда локомотив 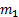 и два вагона начинают тянуть третий вагон
и два вагона начинают тянуть третий вагон 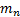 :
:
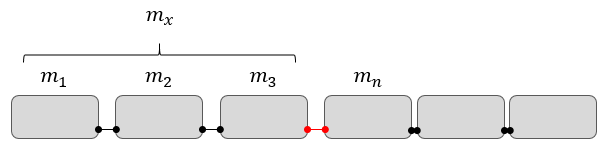
Рис. 2. Пуск поезда.
Вот видео пуска поезда:
Трение
Для вычисления силы трения (переменная m_FrictionForce в WagonPhysicsState) используются формулы и значения, выбранные после серии экспериментов и наиболее соответствующие геймплею. Значение силы трения постоянно, но мы дополнительно масштабируем её согласно текущей скорости (когда скорость ниже 4). Вот график стандартной силы трения для вагонов в игре:
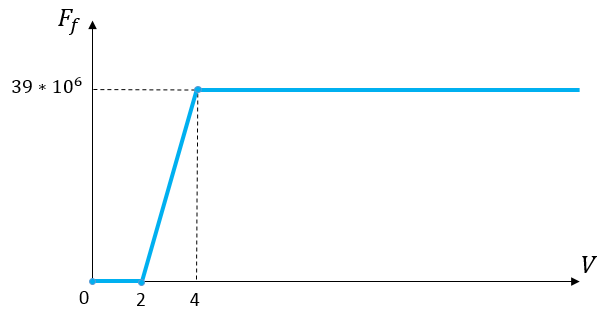
Рис. 3. Стандартная сила трения для вагонов.
Для отсоединённых вагонов используются другие значения:
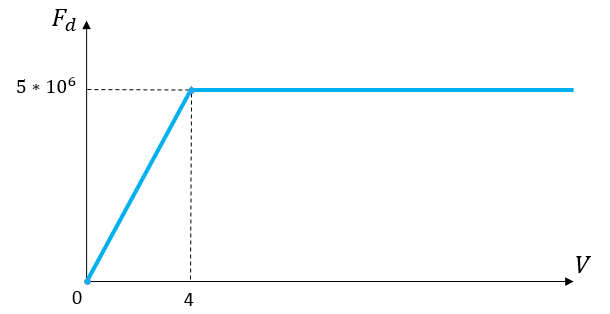
Рис. 4. Сила трения для отсоединённых вагонов.
Кроме того, мы хотели предоставить игроку возможность удобно перепрыгивать с вагона на вагон в течение короткого промежутка времени после отсоединения. Поэтому мы использовали меньшее значение трения и масштабировали его относительно времени, прошедшего после отсоединения вагона. Окончательное значение трения для отсоединённых вагонов задаётся следующим образом:
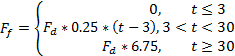
где t — время, прошедшее после события отсоединения (в секундах).
Как можно заметить, мы не используем трение в течение первых трёх секунд, а затем постепенно увеличиваем его.
Последние примечания
В игровых поездах мы добавили подвижные бамперы спереди и сзади вагонов. Эти бамперы не создают никаких физических сил. Мы реализовали их поведение как дополнительный визуальный элемент. Они двигаются согласно обнаруженному смещению соседнего бампера другого вагона.
Кроме того, как можно заметить, мы не проверяем в симуляторе столкновения между разными поездами. Менеджер системы железных дорог несёт ответственность за регулировку скоростей поездов, чтобы избегать столкновений. В нашей симуляции проверяются столкновения только между вагонами одного поезда.
Важно добавить, что в восприятии поездов очень важную роль играют игровые звуки и спецэффекты. Мы вычисляем различные, получаемые из физического поведения, величины для управления звуками и спецэффектами (например, звуками натягивания соединительной стяжки, ударов бамперов, торможения и т.д.).
Итог
Мы рассказали о нашем физическом симуляторе поездов, созданном для Assassin’s Creed Syndicate. Работа над этой частью игры доставила большое удовольствие и была очень сложной. В игровом процессе открытого мира существует множество геймплейных возможностей и различных взаимодействий. Открытый мир создаёт ещё больше сложностей обеспечения стабильных и устойчивых систем. Но после всей проделанной работы очень радостно наблюдать за поездами, перемещающимися в игре и вносящими свой вклад в качество игрового процесса.
Благодарности
Я хочу поблагодарить Джеймса Карнахана (James Carnahan) из Ubisoft Quebec City и Нобуюки Миура (Nobuyuki Miura) из Ubisoft Singapore за редактирование этой статьи и полезные советы.
Также я хочу поблагодарить моих коллег из студии Ubisoft Quebec City studio: Пьера Фортена (Pierre Fortin), который помог мне начать работать с физикой поездов и вдохновлял на развитие; Дейва Трембле (Dave Tremblay) за техническую поддержку; Джеймса Карнахана за все наши разговоры о физике; Матье Пьеро (Matthieu Pierrot) за вдохновляющий подход; Максима Бегина (Maxime Begin), который всегда готов был поговорить со мной о программировании; Винсана Мартино (Vincent Martineau) за помощь. Кроме того, я благодарен Мартену Бедару (Martin Bedard), Марку Паренто (Marc Parenteau), Джонатану Джендрону (Jonathan Gendron), Карлу Дюмону (Carl Dumont), Патрику Шарлану (Patrick Charland), Эмилю Уддестранду (Emil Uddestrand), Дамьену Бастиану (Damien Bastian), Эрику Мартелю (Eric Martel), Стиву Блези (Steve Blezy), Патрику Легаре (Patrick Legare), Гильерму Люпину (Guillaume Lupien), Эрику Жирару (Eric Girard) и всем остальным, работавшим над Assassin’s Creed Syndicate и создавшим такую потрясающую игру!
Справочные материалы
[1] “Buffers and chain coupler”, https://en.wikipedia.org/wiki/Buffers_and_chain_coupler [Прим. пер.: русскоязычная статья на Википедии довольно поверхностна. Подробнее о соединениях, используемых в составах, можно прочитать здесь.]
[2] Andrew Witkin, David Baraff and Michael Kass, “An Introduction to Physically Based Modeling”, http://www.cs.cmu.edu/~baraff/pbm/
[3] Fletcher Dunn, Ian Parberry, “3D Math Primer for Graphics and Game Development, Second Edition”, CRC Press, Taylor & Francis Group, 2011.
[4] David H. Eberly, “Game Physics. Second Edition”, Morgan Kaufmann, Elsevier, 2010.
Автор: PatientZero