В мире алгоритмов: Сортировка Вставками

От автора
Данная статья рассматривает один из алгоритмов сортировки массивов. Она предназначена для новичков или же для тех кто по каким-то причинам не знаком с данным алгоритмом. Исправления и поправки только приветствуются:)

Теория
Сортировка вставками (Insertion Sort) — это простой алгоритм сортировки. Суть его заключается в том что, на каждом шаге алгоритма мы берем один из элементов массива, находим позицию для вставки и вставляем. Стоит отметить что массив из 1-го элемента считается отсортированным.

Словесное описание алгоритма звучит довольно сложно, но на деле это самая простая в реализации сортировка. Каждый из нас, не зависимо от рода деятельности, применял алгоритм сортировки, просто не осознавал это:) Например когда сортировали купюры в кошельке — берем 100 рублей и смотрим — идут 10, 50 и 500 рублёвые купюры. Вот как раз между 50 и 500 и вставляем нашу сотню:) Или приведу пример из всех книжек — игра в карточного «Дурака». Когда мы тянем карту из колоды, смотрим на наши разложенные по возрастанию карты и в зависимости от достоинства вытянутой карты помещаем карту в соответствующее место. Для большей наглядности приведу анимацию из википедии.

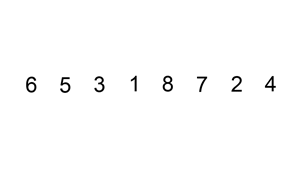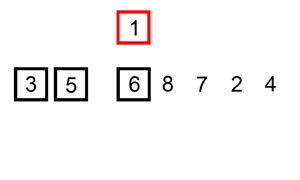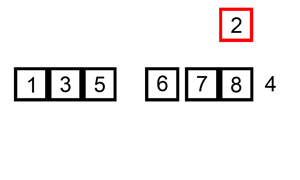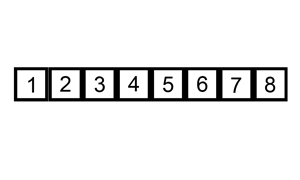
Реализация
Прежде чем приступить к реализации определимся с форматом входных данных — для примера это будет массив целочисленных (int) значений. Нумерация элементов массива начинается с 0 и заканчивается n-1. Сам алгоритм реализуем на языке C++. Итак приступим…
Основной цикл алгоритма начинается не с 0-го элемента а с 1-го, потому что элемент до 1-го элемента будет нашей отсортированной последовательностью (помним что массив состоящий из одного элемента является отсортированным) и уже относительно этого элемента с номером 0 мы будем вставлять все остальные. Собственно код:

for(int i=1;i<n;i++)     
	for(int j=i;j>0 && x[j-1]>x[j];j--) // пока j>0 и элемент j-1 > j, x-массив int
			swap(x[j-1],x[j]);        // меняем местами элементы j и j-1

Реализация сортировки очень проста, всего 3 строчки. Процедура swap меняет местами элементы x[j-1] и x[j]. Вложенный цикл ищет место для вставки. Рекомендую запомнить этот алгоритм, чтобы в случае необходимости написать сортировку не позориться сортировкой пузырьком:)

Анализ производительности
Сортировка вставками имеет сложность n² на практике же приблизительное количество перестановок вычисляется по формуле n²/2. Для доказательства был написан следующий код:

void Sort(int* arr,int n){
	int counter=0;
	for(int i=1;i<n;i++){
		for(int j=i; j>0 && arr[j-1]>arr[j];j--){
			counter++;
			int tmp=arr[j-1];
			arr[j-1]=arr[j];
			arr[j]=tmp;
		}
	}
	cout<<counter<<endl;
}

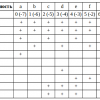
Количество перестановок для 100 элементов:

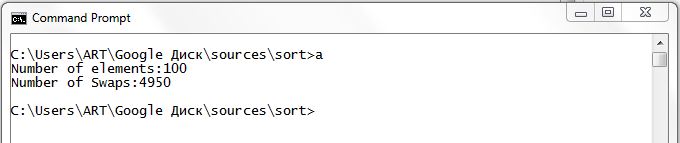
Итак при n=100 количество перестановок равно 4950, а не 10000 если бы мы высчитывали по формуле n². Имейте это ввиду при выборе алгоритма сортировки.

Эффективность
Сортировка вставками наиболее эффективна когда массив уже частично отсортирован и когда элементов массива не много. Если же элементов меньше 10 то данный алгоритм является лучшим. Не зря в быстрой сортировке (оптимизация Боба Седжвика) используется алгоритм сортировки вставками как вспомогательный, но об этом алгоритме мы поговорим позже…

Автор: artem_drozdoff

Источник