Иногда, если имеешь дело с числовыми последовательностями или бинарными данными, возникает желание “пощупать” их, понять, как они устроены, подвержены ли сжатию, если зашифрованы, то насколько качественно. Если речь идет о генераторах псевдо-случайных чисел, хочется знать, насколько они псевдо и насколько случайны.
В самом деле, что тут можно придумать, ну … матожидание, дисперсию посчитать или гистограмму какую построить…
Сейчас мы рассмотрим метод, позволяющий снимать, своего рода, отпечатки пальцев с числовых последовательностей.
- Пусть у нас есть генератор целых чисел, способный выдавать их достаточно много (10 000 000 в нашем случае).
- Выберем размер отпечатка, который сейчас будем “катать”, пусть Sz=1024
- Выделяем и обнуляем память для целочисленной двумерной квадратной матрицы размером Sz: Hists[Sz][Sz]
- Вычитываем из генератора числа и для каждого из них (Val) организуем цикл
for (size_t ix = 1; ix <= Sz; ix++) { size_t histix = Val % ix; Hists[ix-1][histix] ++; }Т.е. мы строит гистограммы остатков от деления входных значений на все числа в пределах выбранного размера отпечатка Sz.
- После прогона достаточного количества сгенерированных значений, у нас есть двумерная гистограмма остатков от деления на все числа в выбранном диапазоне. Отметим, что эта гистограмма не зависит от порядка, в котором генератором выдаются значения. С другой стороны, мы могли бы скармливать гистограмме не сами значения, а их отличия от предыдущего, например, тогда и порядок был бы частично учтен
- Далее мы выводим полученную гистограмму в удобном для просмотра виде (здесь использован gnuplot в режиме ‘pm3d map’) и любуемся открывшейся картиной. Стоит отметить, что в выдачу попадает не значение из Hists[ix][[iy], а скорректированное с учетом вероятности попадания (Hists[ix][iy]*(ix+1)/Sz)
Итак, начнем. А начнем мы со стандартного С-шного генератора rand:
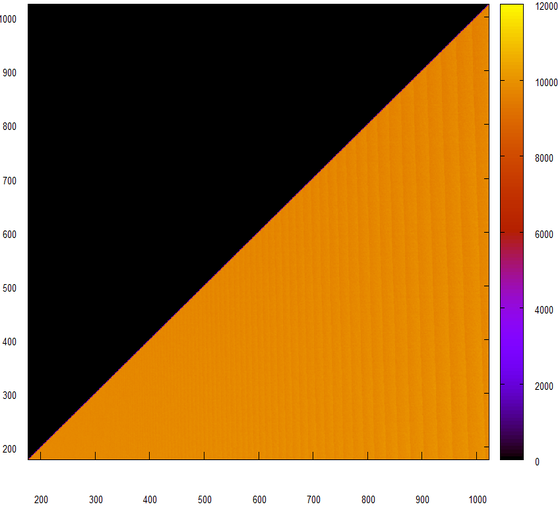
Ожидаемо, гистограмма получилась треугольная и плоская, но… а что это за странные полоски?
Рассмотрим подробнее.
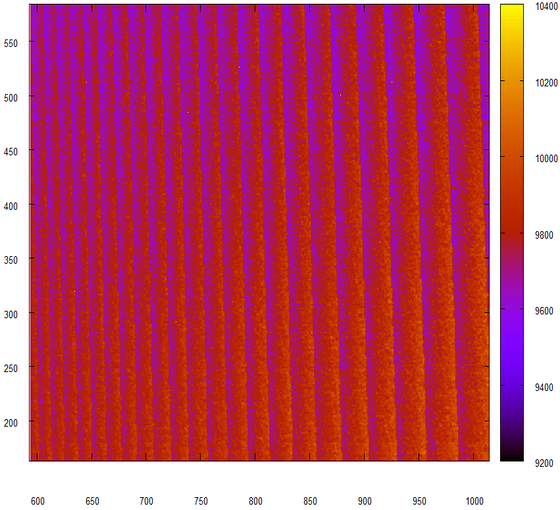
Похоже, этот генератор выдает не очень случайные числа. Ну что же, я всегда подозревал, что использование rand() в качестве генератора случайных чисел — “это верный признак дурного человека”(С).
Пожалуй, стоит посмотреть на “правильный” генератор случайных чисел. В качестве такового мы будем использовать оный, любезно предоставленный как-то Юрием Ткачевым.
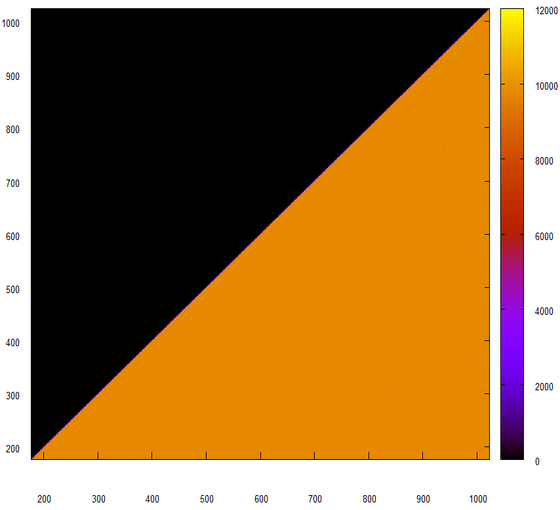
На первый взгляд выглядит неплохо. Присмотримся к этой гистограмме.
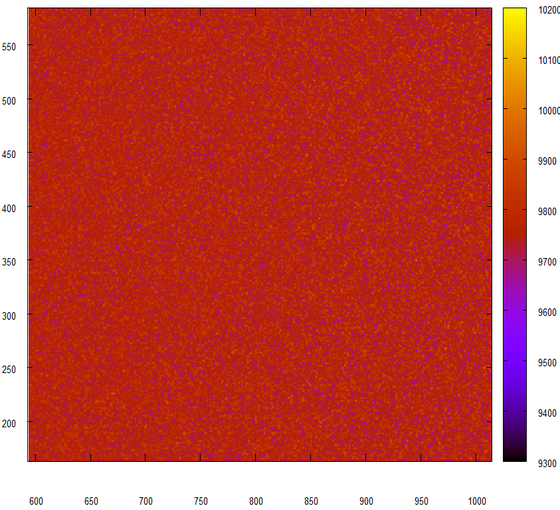
Да, это как раз то, что мы и ожидали получить от генератора случайных чисел. Попробуем немного пошевелить данные, будем учитывать только младшие 24 бита.
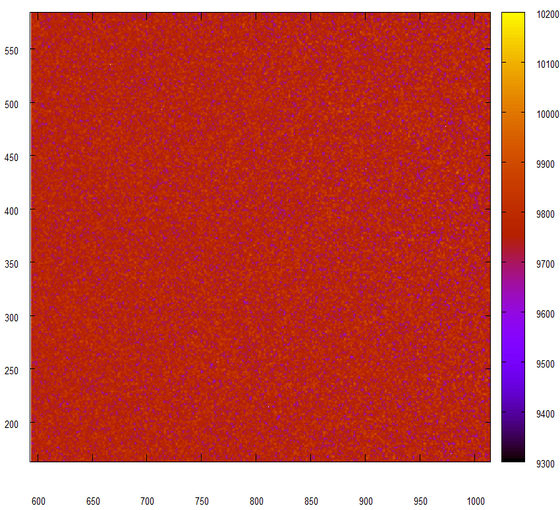
Ничего не изменилось, но ведь именно это мы и хотели увидеть. Еще эксперимент, на этот раз мы будем склеивать куски по 24 бита из двух последовательных чисел, выданных нашим замечательным генератором.
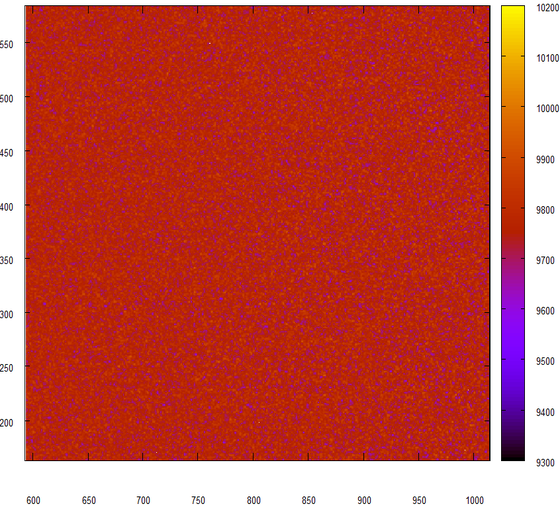
И опять никаких отличий! Просто великолепно!
Последняя попытка, на этот раз мы будем не склеивать 24-битовые куски, а перемножать их.
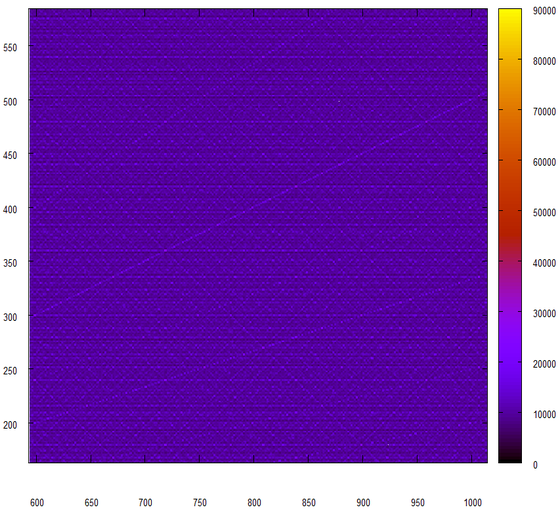
Бац! И такое ощущение, что из нашего генератора случайных чисел вылезло его псевдо-нутро.
То же, но в в другом масштабе:
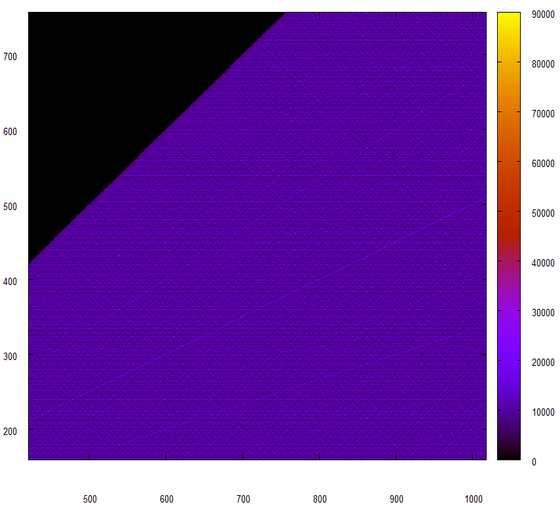
Ой-ой “сказали мы с Петром Ивановичем”(С).
Чтобы перевести дух и выиграть время для осмысления произошедшего, посмотрим, как выглядят данные другого рода:
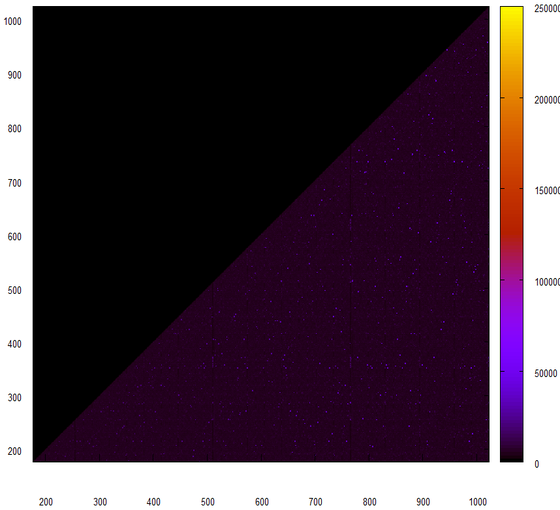
Вот это первые 10 млн 64-разрядных целых чисел, вычитанных из файла — образа базы данных.
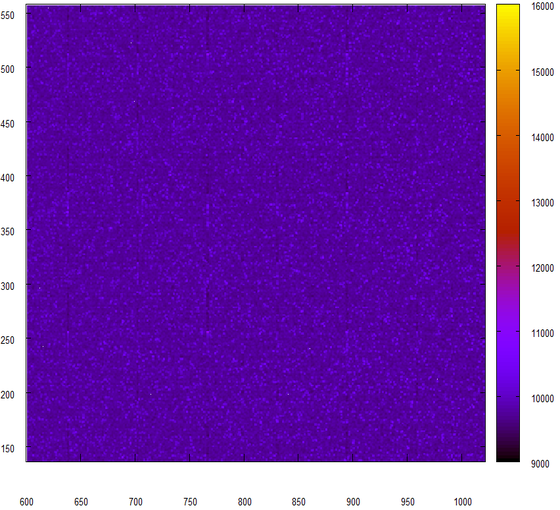
А вот так выглядят полученные таким же образом данные, источником которых служил zip-файл.
Это было бы похоже на случайные данные, но вертикальные полоски всё портят.
Так вот, пока внимательный читатель забавлялся чтением данных из файлов, автор решил посмотреть как ведут себя очень даже неслучайные последовательности. Начнем с F(n) = F(n-1) + 1 т.е. 0, 1, 2, 3…
Гистограмму самой последовательности и смотреть не будем, она треугольная и совершенно плоская, что интуитивно понятно и легко объяснимо. В самом деле, поскольку в наш метод не заложен порядок, такая последовательность ведет себя как идеальный генератор случайных чисел, который равновероятно заметает весь диапазон.
А вот распределение произведения из двух чисел, каждое от 0 до 4000 выглядит так:
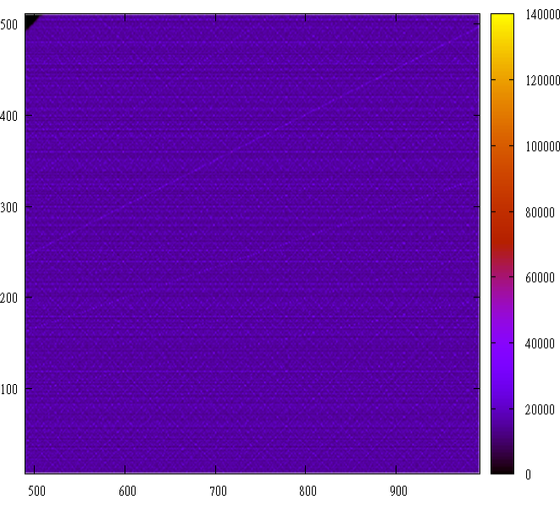
Очень знакомая картинка, не правда ли. Фактически, мы видим эталонный образец гистограммы произведения двух чисел.
В одном месте сошлись произведение и остатки от деления.
Довольно незатейливым образом мы вытащили из под полы магию чисел.
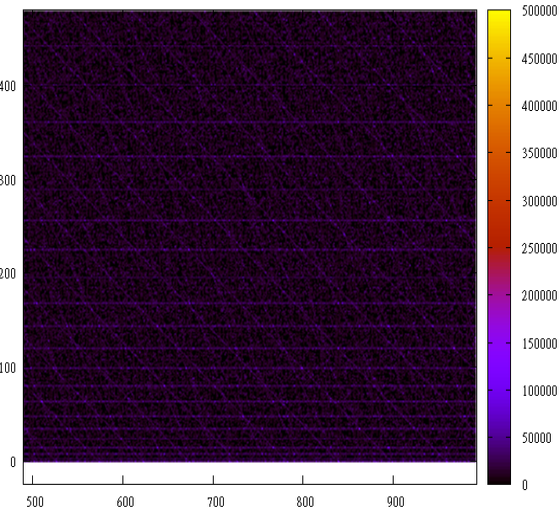
А вот так ведет себя последовательность F(n) = n * n т.е. 0, 1, 4, 9…
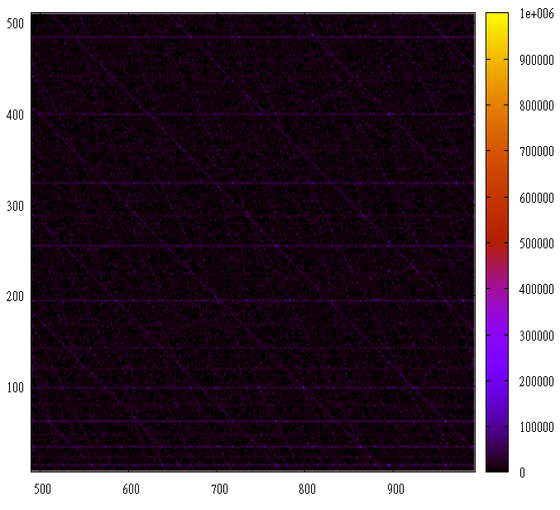
А здесь F(n) = 2 * n * ( 2 * n + 1) т.е. 0*1, 2*3, 4*5…
Ну и напоследок автор не смог удержаться от показа распределения первых 10 млн простых чисел.
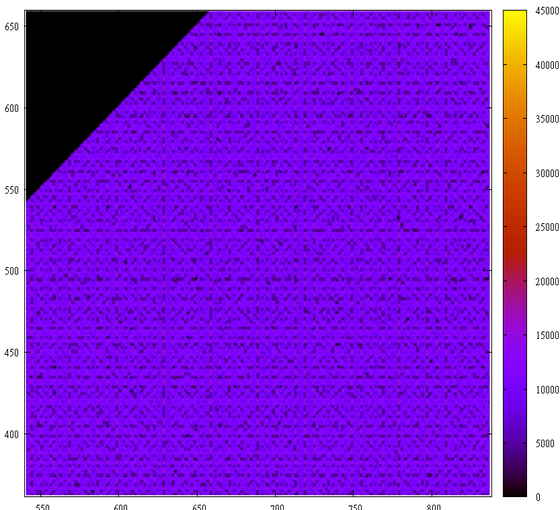
И их “слепка” — первых 10 млн непростых чисел (просто красиво).
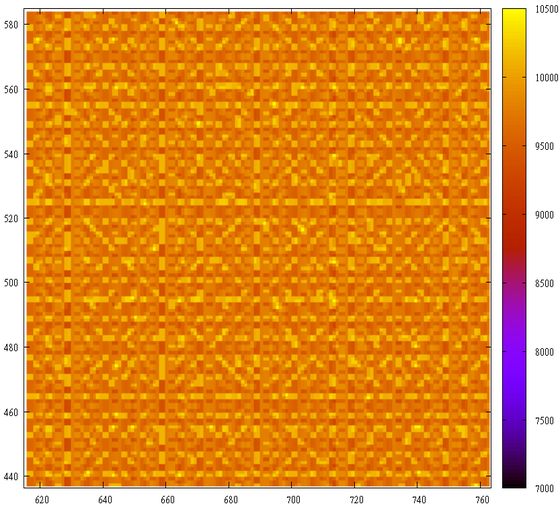
Что ж, будьте бдительны и “всегда, нет, никогда”(С) не перемножайте последовательности:).
PS. Отдельную благодарность автор выражает Александру Артюшину за деятельное обсуждение subj.
Автор: zzeng