Квантовая физика и алгоритм Брезенхема

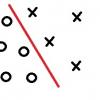
Если пространство недискретно, то почему Ахиллес обгоняет черепаху? Если же пространство дискретно, то как частицы реализуют алгоритм Брезенхема?

Я давно задумываюсь над тем, что собою представляет Вселенная в целом и законы её работы в частности. Порою описания некоторых физических явлений на той же Википедии достаточно запутаны, чтобы оставаться непонятными даже для человека, который не шибко далёк от данной области. Тем более не повезло мне подобным — тем, кто от этой области по крайней мере был весьма далёк. Однако, с несколько другой плоскостью — алгоритмами, я, будучи программистом, сталкиваюсь почти ежедневно. И однажды, в процессе реализации некоего подобия 2d-физики в консоли, я подумал: «А ведь Вселенная — это по сути такая же консоль неизвестной размерности. Есть ли причины думать, что для линейного движения на, так сказать, экране этой консоли, частицы не должны реализовывать алгоритм Брезенхема?». И кажется, причин нет.

Всех, кому интересно, что вообще такое алгоритм Брезенхема, как он может быть связан с физикой и как это может повлиять на её интерпретацию — добро пожаловать под кат. Возможно, Вы найдёте там косвенное подтверждение существования параллельных Вселенных. Или даже вложенных друг в друга Вселенных.

Алгоритм Брезенхема

Говоря простым языком, чтобы нарисовать на тетрадном листке в клеточку линию толщиной в одну клетку, Вам понадобится закрашивать последовательно идущие клетки, стоящие в ряд. Предположим, что плоскость тетрадного листка дискретна по клеткам, то есть Вы не можете закрасить две соседних половинки соседних клеток и сказать, что закрасили клетку со смещением в 0.5, ибо дискретность заключается в непозволении подобного действия. Таким образом, закрашивая последовательно клетки, стоящие в ряд, Вы получите отрезок желаемой длины. Теперь представим, что Вам необходимо повернуть его на 45 градусов в любом направлении — теперь уже Вы будете закрашивать клетки по диагонали. По сути это — прикладное применение нашим мозгом двух простейших функций:

f(x) = 0

и

f(x) = x

А теперь представим, что отрезок необходимо повернуть ещё на 10 градусов, например. Тогда мы получим классическую однородную линейную функцию:

f(x) = x * tan(55)

И нарисовать график этой функции обычной ручкой на обычном листке не составит труда для любого ученика 7 класса. Однако что делать в случае с нашим предполагаемым листком бумаги, который дискретен по клеткам? Ведь тогда возникает необходимость выбирать, какие именно клетки закрашивать при рисовании линии. Тут нам на помощь и приходит алгоритм Брезенхема.

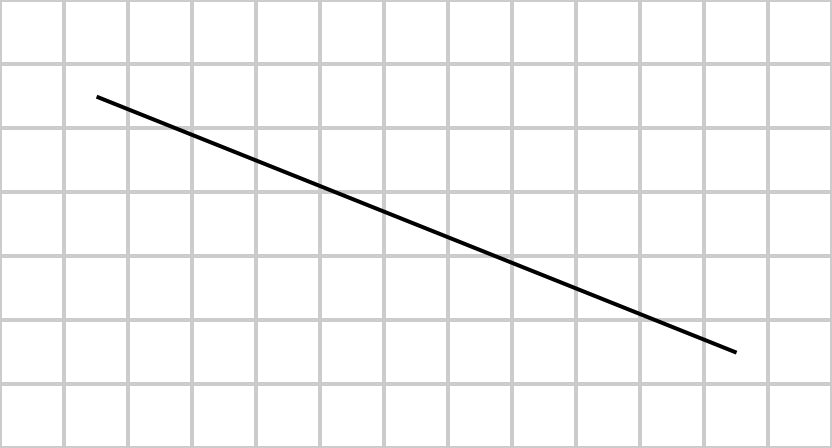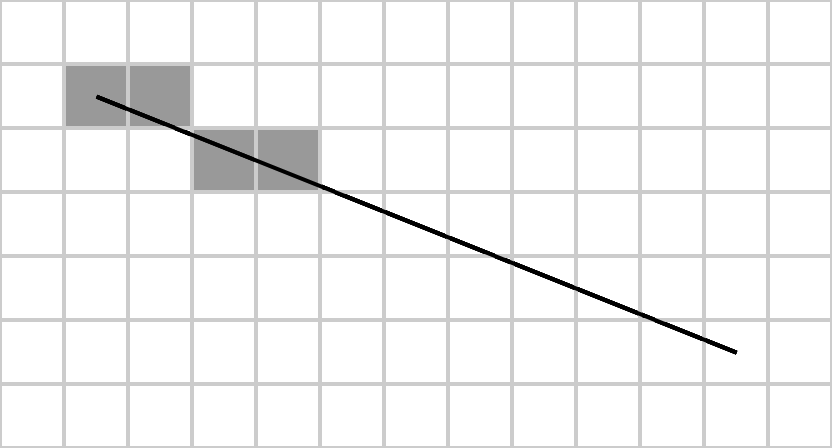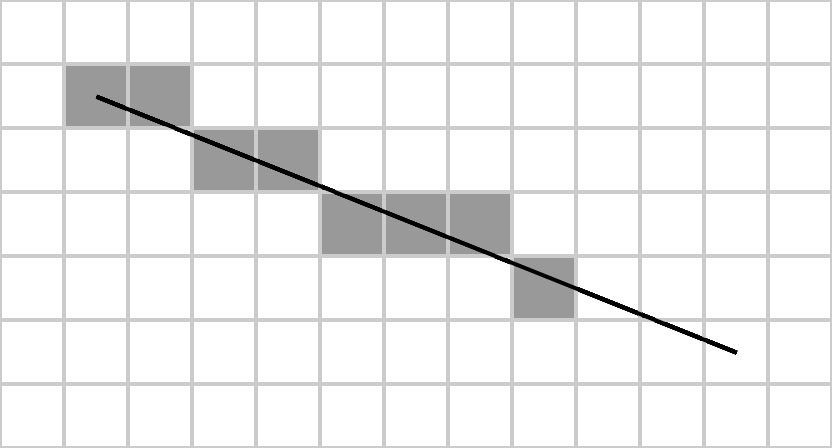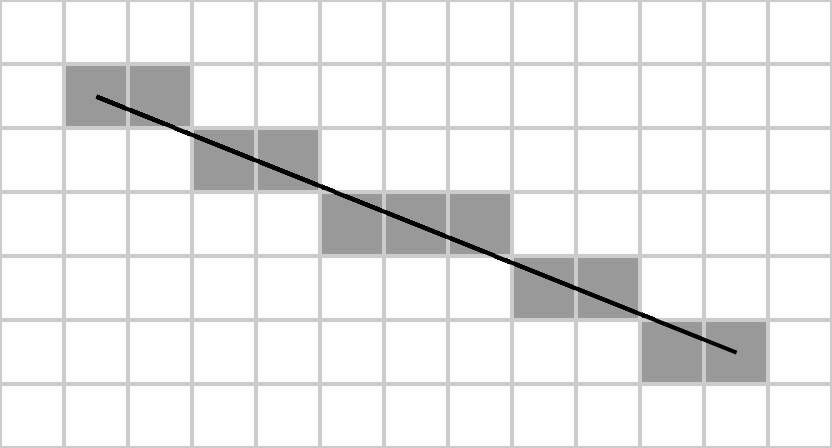
Сей аглоритм был разработан Джеком Брезенхемом в 1962 году, когда тот работал в IBM. Он до сих пор используется для реализации виртуальной графики во многих прикладных и системных комплексах, начиная с оборудования на производстве и заканчивая OpenGL. Используя этот алгоритм, можно рассчитать максимально подходящее приближение для заданной прямой при заданном уровне дискретности плоскости, на которой эта прямая располагается.

var draw = (x, y) => { ... }; // функция для рисования точки
var bresenham = (xs, ys) => {
    // xs, ys - массивы [x1, x2] и [y1, y2] соответственно
    let deltaX = xs[1] - xs[0],
        deltaY = ys[1] - ys[0],
        error = 0,
        deltaError = deltaY,
        y = ys[0];
    for (let x = xs[0]; x <= xs[1]; x++) {
        draw(x, y);
        error += deltaError;
        if ((2 * error) >= deltaX) {
            y -= 1;
            error -= deltaX;
        };
    };
};

А теперь представьте, что пространство, которое окружает нас, всё таки дискретно. Причём не важно, заполнено ли оно ничем, частицами, переносчиками, полем Хиггса или ещё чем — есть некое понятие минимального количества пространства, меньше которого ничто не может быть. И не важно, относительно ли оно и верна ли теория относительности касательно него — если пространство искривлено, то локально там, где оно искривлено, оно всё равно будет дискретно, даже если с другой позиции может показаться, будто имело место быть изменение того самого минимального порога в любую сторону. При таком предположении получается, что некое явление, или сущность, или правило, должно реализовывать алгоритм Брезенхема для любого рода движения как частиц материи, так и переносчиков взаимодействий. В какой-то мере это объясняет квантование движения частиц в микромире — они принципиально не могут двигаться линейно, не «телепортируясь» из кусочка пространства в другой кусочек, ибо тогда получится, что пространство вовсе не дискретно.

Возможно, я попал в порочный круг. Однако, есть несколько неоднозначной полноты аргументов в пользу того, что пространство всё таки дискретно.

Почему Ахиллес обгоняет черепаху?

Однажды древнегреческий философ Зенон описал подобную ситуацию:

Быстроногий Ахиллес никогда не догонит неторопливую черепаху, если в начале движения черепаха находится впереди Ахиллеса. Допустим, Ахиллес бежит в десять раз быстрее, чем черепаха, и находится позади неё на расстоянии в тысячу шагов. За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползёт сто шагов. Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.

Взято отсюда. На самом деле, для опровержения подобного заявления можно прибегнуть к рассуждениям о сходимости рядов, или же упростить абстракцию: на самом деле Ахиллес обгоняет черепаху потому и только потому, что в какой-то момент расстояния между черепахой и Ахиллесом и между черепахой и следующей её позицией становятся равны. Таким образом, в следующий момент Ахиллес, обладая большей скоростью, сравняется с черепахой, а затем и перегонит её. Я могу ошибаться, но кажется, это прямое доказательство дискретности пространства с помощью мысленного эксперимента. Ибо, если пространство может быть бесконечно мало, то Ахиллес никогда не достигнет момента «сразу за черепахой», а всегда будет на расстоянии бесконечного количества кусочков пространства позади неё.

Время шло, и место мыслителей Древней Греции заняли относительно современные физики. Так, в 1899 году Макс Планк, основываясь на реальных физических величинах, предложил миру планковскую систему единиц, в коей, среди прочих, имеет место быть планковская длина. Суть суждений Планка о минимально возможной длине пространства, доступной для предсказуемого взаимодействия, строится на гипотезе о том, что масштабы наблюдаемого и приближение этого наблюдаемого к евклидовой геометрии — значения прямо коррелирующие. Говоря проще: чем больше объект, тем точнее он описывается с помощью евклидовой геометрии, и наоборот. Евклидова геометрия — это, грубо говоря, та, которая не Лобачевского в которой через одну точку можно провести только одну прямую, параллельную данной. Таким образом, следуя гипотезе о корелляции «уровня евклидности» и масштабов, можно заявить, что имеет место быть некий нижний порог размера пространства, при пресечени которого объект или явление в этом участке пространства уже нельзя описывать с помощью евклидовой геометрии. Макс Планк знал гравитационную постоянную и скорость света, а также некоторые параметры фотона и с помощью этих данных вычислил данный порог: он равен примерно 1,616229(38) * 10 ^-35 м. Исходя из умозаключений о том, что существует данный предел, кто-то предположил, что если он есть, то он должен влиять на квантование движения фотонов. Другими словами, поведение фотонов должно отличаться при различных уровнях настоящей минимальной длины пространства. Так, примерно 300 миллионов лет назад что-то в космосе вспыхнуло достаточно сильно, чтобы 28 марта 2011 г. редакция журнала APS Physics получила данные об этой вспышке от NASA, где её назвали GRB 041219A. Эта гамма-вспышка вошла в 1% самых ярких вспышек в истории наблюдений за космосом и, основываясь на данных её съёмки, учёные пришли к выводу о том, что размер зерна пространства, если предположить, что оно дискретно, должен быть примерно равен 10 ^-48 м. ^{[1] [2]}

Ещё одним косвенным подтверждением дискретности пространства может служить суждение, исходящее из вышеописанного: если при определённом уменьшении масштабов наблюдаемого, сие теряет способность быть описанным с помощью евклидовой геометрии, то очевидно, что при преодолении минимального порога расстояния метод геометрического описания субъекта всё равно должен быть. Пусть в такой геометрии одной параллельной прямой может соответствовать более одной другой прямой, проходящей через точку, не принадлежащую исходной прямой, или в такой геометрии вообще нет понятия параллельности прямых или даже вовсе понятия прямых, однако имеет место быть любой, гипотетически представляемый метод описания геометрии объекта меньше минимальной длины. И, как известно, есть одна теория, претендующая на способность описать такую геометрию в пределах известного минимального порога. Это теория струн. Она предполагает существование чего-то, что учёные зовут струнами или бранами, сразу в 10/11/26 измерениях в зависимости от интерпретации и математической модели. Мне лично кажется, что примерно так всё и обстоит и для обоснования своих слов я проведу с Вами мысленный эксперимент: на двумерной плоскости при полной «евклидности» её геометрии работает уже упоминавшееся правило: через одну точку можно провести только одну прямую, параллельную данной. Теперь масштабируем это правило на трёхмерное пространство и получим два из него вытекающих новых правила:

1. Аналогичное — через одну точку можно провести только одну прямую, параллельную данной
2. На указанном расстоянии от данной прямой может быть бесконечность-X прямых, и эта бесконечность-X в Y раз меньше бесконечности-Z всех прямых, параллельных данной, независимо от расстояния, где Y — это, грубо говоря, возможное количество толщин прямой в пределах пространства

Говоря проще, если добавить измерение при построении прямых, но не добавлять измерение при расчёте подчинения прямых правилам евклидовой геометрии, то вместо двух возможных параллельных прямых, получим «цилиндр» возможных прямых вокруг центра — исходной прямой. А теперь представьте, будто мы живём в мире Супер Марио и пытаемся спроецировать такой цилиндр на собственное двумерное пространство — по рассчётам параллельных прямых быть не может, но по наблюдениям их целая бесконечность-X. Что мы предположим? Правильно, мы введём ещё одно измерение для построения прямых, но не станем добавлять его для расчёта подчинения прямых правилам евклидовой геометрии. По сути, увидев проекцию такого цилиндра на родное двумерное пространство мы придумаем теорию струн в своём двумерном мире.

Параллельные и вложенные Вселенные?

Может оказаться так, что древние философы, которые видели в модели атома поведение небесных тел и наоборот, были, скажем, не шибко дальше от истины, чем те, кто утверждал, будто это полная чушь. Ведь если освободиться от всяких знаний и рассудить логически — теоретически нижний предел есть не более чем фикция, придуманная нами для ограничения действия привычной нам евклидовой геометрии. Говоря другими словами — всё, что меньше планковской длины, а точней, так сказать настоящей планковской длины, просто не поддаётся исчислению методами евклидовой геометрии, однако же это не значит, будто оное не существует! Вполне может оказаться так, что каждая брана — это набор мультивселенных и так сложилось, что в пределах от планковской длины до неизвестного X геометрия реальности евклидова, ниже планковской длины — например главенствует геометрия Лобачевского или сферическая геометрия, или ещё какая, никак не ограничивая наш полёт фантазии, а выше предела X — например одновременно недезаргова и сферическая геометрия. Мечтать не вредно — могли бы сказать Вы, коли б не тот факт, что даже для однозначно квантового движения, не говоря уже о линейном (которое всё равно квантуется на уровне микромира) частицы должны реализовывать алгоритм Брезенхема, если пространство дискретно.

Иначе говоря, или Ахиллес никогда не догонит черепаху, или мы в Матрице вся обозримая Вселенная и известная физика, скорей всего — лишь капля в огромном океане возможного разнообразия реальности.

1. Публикация в журнале APS Physics о съёмке гамма-вспышки GRB 041219A.
2. Доклад NASA об обнаружении и исследовании этой вспышки.

Автор: лейтенант Буэндиа

Источник