Прошло два месяца с момента моей предыдущей публикации о конкурсах по функциональному программированию, и я спешу порадовать заинтересованных читателей новым отчётом о проведённом конкурсе. На этот раз, в декабре, я немного сплоховал, из-за чего конкурс получился смазанным, скомканным. Хотя, по свидетельству одного из участников, задача была интересной, несмотря на то, что это опять поиск по дереву состояний. Но у меня на работе была сдача одного из проектов, поэтому я опубликовал заготовленную задолго заготовку, а прорекламировать конкурс и позабыл. В итоге приняло участие только два человека. Ну и вы сами можете всё это изучить: условие, результат.
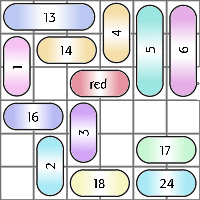
В качестве задачи участникам была сформулирована необходимость реализовать решатель для игр типы Rush Hour или Traffic Jam — на квадратной парковке при помощи использования свободных мест для разгребания заблокированного пути необходимо освободить «красную» машину — своеобразные «расширенные пятнашки». В общем, я думаю, большинство читателей понимает, о чём речь.
Собственно, на конкурс было представлено два решения — одно на языке программирования Clojure, а второй — на JS. В честь того, что конкурс был заключительным в этом году, призы уже получили все участники. Ну а я традиционно представлю решение конкурсной задачи на языке программирования Haskell. Так что если кому-то интересно —
Реализация решения на языке Haskell
Прежде всего необходимо определить все требуемые типы данных. У нас имеется две главные сущности — парковка и машины на ней. Так что для этих сущностей и определим типы:
data Car = Vertical
{
place :: Place,
lngth :: Length
}
| Horizontal
{
place :: Place,
lngth :: Length
}
deriving (Eq, Ord, Show)
Это описание одной машины. Машина может быть расположена вертикально или горизонтально. У каждой машины, независимо от способа её расположения, есть два параметра — координата её «головы» и длина в клетках парковки. Соответственно, для парковки определяются её размеры в клетках, а также задаётся список стоящих на ней машин. При этом выделяется «красная» машина. Это определяется следующим образом:
data Parking = Parking
{
board :: Board,
redCar :: Car,
cars :: [Car]
}
deriving (Eq, Ord, Show)
Идентификаторы Place, Length и Board являются простыми синонимами ради украшательства:
type Board = (Int, Int)
type Place = (Int, Int)
type Length = Int
Собственно, теперь всё готово для реализации решения. Начнём, как обычно, сверху. Вот определение функции solve, которая решает задачу при помощи всем известного алгоритма A*. Ничего в этом примечательного нет, поскольку решатели для всех подобных задач проще всего быстро закодировать именно при помощи алгоритма A*.
solve :: Parking -> Maybe [Parking]
solve = aStar neighbours (_ _ -> 0) (const 0) goal
Здесь не используются функции для вычисления расстояния между состояниями и эвристики, хотя можно было бы придумать что-нибудь этакое. Например, расстоянием может быть количество клеток, на которые отодвигается машина. А эвристикой может служить, например, то, что если в результате перехода к новому состоянию освобождается путь «красной машине», такое состояние более предпочтительно. Однако здесь необходимо исследование, поскольку подобные подходы могут снизить эффективность алгоритма.
ФП(ФП)-2013: ИРИДИЙ
Теперь продолжим рассмотрение с предиката goal, который определяет целевые состояния для поиска. Когда этот предикат даёт на очередном шаге поиска на полученном состоянии значение True, поиск останавливается. Вот его определение:
goal :: Parking -> Bool
goal p = case redCar p of
Vertical (x, y) _ -> all (not . isThereAnyCar (redCar p) p) [(x, y') | y' <- [y .. snd (board p)]]
Horizontal (x, y) _ -> all (not . isThereAnyCar (redCar p) p) [(x', y) | x' <- [x .. fst (board p)]]
В общем-то, всё просто. Берём «красную» машину и в зависимости от того, вертикально она расположена или горизонтально (это — элемент универсальности решения; во всех виденных мною играх такого рода «красная» машина расположена горизонтально, имеет 2 клетки в длину и находится на третьей горизонтали) смотрится, есть ли перед ней до конца парковки какие-либо машины. Если машин нет, то есть путь свободен, то состояние определяется как целевое.
Здесь в определении используется функция isThereAnyCar, которая возвращает значение True тогда, когда на заданной клетке парковки есть какая-либо машина. Она определяется так:
isThereAnyCar :: Car -> Parking -> Place -> Bool
isThereAnyCar c p (x, y) = any isThereACar $ removeCar c $ redCar p : cars p
where
isThereACar (Vertical (x', y') l) = (x == x') && (y >= y') && (y <= y' + l - 1)
isThereACar (Horizontal (x', y') l) = (y == y') && (x >= x') && (x <= x' + l - 1)
Эта функция определена специальным образом. Она вычисляет требуемое значение для некоторой заданной машины, которую мы намереваемся двигать на следующем шаге. Это значит, что саму эту машину необходимо исключать из списка машин, которые проверяются, не находятся ли они на заданном месте на парковке. Это делается при помощи функции removeCar, определение которой следующее:
removeCar :: Car -> [Car] -> [Car]
removeCar c' cs = l1 ++ l2
where
(l1, _:l2) = break (((==) `on` place) c') cs
Можно было бы воспользоваться функцией delete из модуля Data.List, а не городить этот «велосипедик», но так уже вышло, из кода определения не выкинешь.
Теперь перейдём к определению функции, возвращающей множество соседних состояний для поиска neighbours. Вот её определение:
neighbours :: Parking -> Set Parking
neighbours p = S.unions $ map neighbours' $ redCar p : cars p
where
neighbours' c = case c of
Vertical (x, y) l -> S.fromList $
map (replaceCar c) $
filter (not . intersects c p)
[(x, y') | y' <- [1 .. snd (board p)],
y' < y || y' > y && y' + lngth c - 1 <= snd (board p)]
Horizontal (x, y) l -> S.fromList $
map (replaceCar c) $
filter (not . intersects c p)
[(x', y) | x' <- [1 .. fst (board p)],
x' < x || x' > x && x' + lngth c - 1 <= fst (board p)]
replaceCar c xy = if ((==) `on` carX) c (redCar p) && ((==) `on` carY) c (redCar p)
then Parking (board p) c{place = xy} $ cars p
else Parking (board p) (redCar p) $ findAndMoveCar c (cars p) xy
Тут есть опять два однотипных куска кода, относящихся к вариантам, когда машина расположена вертикально и горизонтально. Получается так, что для каждой машины списка, в том числе и для «красной» машины, берутся все свободные клетки, которые расположены на той же вертикали или горизонтали, и по ним смотрится, может ли машина на них попасть (не пересекается ли при этом с другой машиной). Если не пересекается, то такое новое состояние добавляется в возвращаемое множество.
Тут используется несколько определений дополнительных функций. В первую очередь, это предикат, который для заданной машины и положения на парковке определяет, пересекает ли эта машина на заданном месте какую-либо другую машину. Вот его определение:
intersects :: Car -> Parking -> Place -> Bool
intersects c p (x, y) = any (isThereAnyCar c p) carPlaces
where
carPlaces = case c of
Vertical _ lngth -> [(x, y') | y' <- [y .. y + lngth - 1]]
Horizontal _ lngth -> [(x', y) | x' <- [x .. x + lngth - 1]]
И, наконец, определение трёх совсем уж служебных функций, чьи определения говорят сами за себя:
carX :: Car -> Int
carX = fst . place
carY :: Car -> Int
carY = snd . place
findAndMoveCar :: Car -> [Car] -> Place -> [Car]
findAndMoveCar c' cs xy = l1 ++ c{place = xy}:l2
where
(l1, c:l2) = break (((==) `on` place) c') cs
Всё…
В представленной реализации есть, как минимум, четыре явных недочёта, над которыми предлагается подумать пытливым читателям:
- Плохо, что для типов
CarиParking(особенно для второго) не реализован специальный экземпляр классаShowдля приятного глазу представления парковки. Можно было бы рисовать при помощи псевдографики саму парковку, например. - Для решения задачи важен алгоритм действий, а не набор состояний парковки, что возвращает алгоритм А*. Поэтому, в идеале, решение необходимо дополнить тем, что программа должна выводить перечень действий типа «Передвинуть машину с клетки (X1, Y1) на клетку (X2, Y2)» или ещё как-то.
- Всё-таки можно и нужно поразмыслить над функцией вычисления расстояния и эвристикой для реализации алгоритма A*
- В представленной реализации решения есть одна логическая ошибка (в функции вычисления соседних состояний), которая приводит к неприятным последствиям для сложных конфигураций. Кто первый в комментариях укажет на неё — получит приз.
Как всегда с разработанным исходным кодом всякий желающий может ознакомиться здесь.
Мои предыдущие статьи о конкурсах по ФП на Хаброхабре:
- Конкурсы в 2011 году: Альманах конкурсов по ФП за 2011 год
- Конкурсы в 2012 году: Альманах конкурсов по ФП за 2012 год
- Игра в «кошки — мышки», поиск минимальной стратегии
- Немного стеганографии: о подготовке апрельского конкурса по ФП
- Июньский конкурс по ФП: поиск закодированной фразы мудреца
- Игра Wordament — реализация помощника на языке Haskell
- Rocket Science for Fun and Fun. Запускаем космические корабли
Автор: Darkus
