О близости вершин

«До того, как вы постигнете это, оно кажется чудом. Но после в нем нет ничего особенного.»

Не, не про горы, — про графы. В математике есть вопросы, формулировка которых доступна каждому, а вот решение нетривиально и без специальной подготовки трудно объяснимо. Одну из подобного рода проблем кратко можно выразить так — как правильно считать расстояния в направленных графах? Данную несколько абстрактную проблему можно свести к вполне конкретной мотивирующей задаче. Она умещается на одном рисунке:

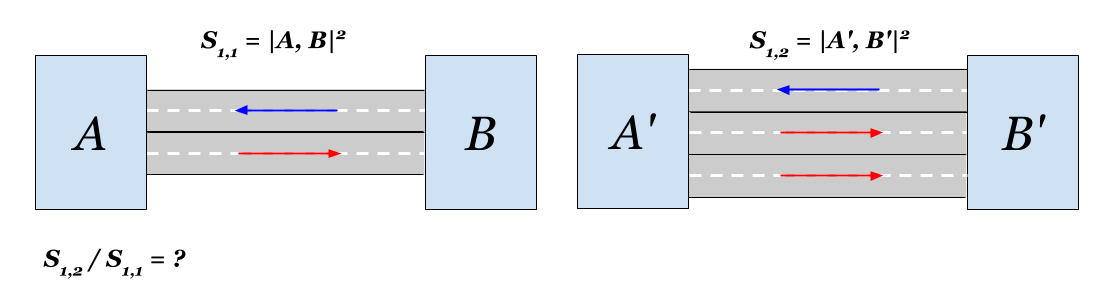
1. Постановка задачи. Я живу на одном, ну а ты на другом.

Небольшой городок разделен (например, рекой, хотя в контексте вершин более подходит ущелье) на два района (части) и . Сообщение между районами осуществляется по единственной дороге (мосту), имеющей две полосы: в сторону от к и обратно. В связи с ростом населения встал вопрос об увеличении пропускной способности дороги. Денег как обычно в обрез и хватает только на одну полосу в одном направлении. Понятно, что даже одна полоса сблизит районы, но вот вопрос — насколько именно? Вы — городской сумасшедший математик, и именно вас пригласили для того, чтобы получить обоснованный ответ.

Насколько будут ближе районы, если построить еще одну полосу в одном направлении?

Формулировка для продвинутых

Вместо кёнигсбергских мостов можно использовать чуть более строгий язык теории графов. Итак, есть направленный граф с двумя вершинами (узлами) и . Величина связи (проводимость, пропускная способность) в прямом и обратном направлении изначально равны. Вопрос — насколько изменится расстояние между узлами, если проводимость в одном из направлений увеличить вдвое?

И да, если вы настоящий сварщик математик, то сможете предложить (и обосновать) решение для любых значений прямой и обратной связей. В идеале — для графа с любым количеством узлов и связей.

Мера близости и пьяные блуждания

Понятно, что обычное (километровое) расстояние между районами не зависит от наличия или отсутствия дороги. Поэтому тут не подойдет,- нам надо опираться на связи. Чем более районы связаны — тем они ближе, — больше жителей могут добраться до другого района в единицу времени.

Для оценки меры близости между узлами ненаправленного графа можно использовать так называемое резистивное расстояние. Ранее мы уже описывали на хабре свойства данного расстояния в нескольких статьях.

Резистивное расстояние эквивалентно понятию эффективного сопротивления, если речь идет об электрической сети. Поэтому на электрическом языке задачу можно сформулировать так. Между двумя узлами встречно включены два диода равных проводимостей. Как изменится сопротивление между данными точками, если добавить еще один диод? (Извиняюсь, если электрический язык подвел и я ерунду тут написал).

Также эффективное сопротивление можно трактовать на марковском языке вероятностей пьяных случайных блужданий (желающим углубиться в тему — гуглить «Random walks and electric networks»).

Резистивное расстояние квадратично, — соответствует квадрату линейного расстояния. Квадратичные расстояния называют также квадрансами. Но поскольку другие (линейные) расстояния в данной задаче не используются, то и термин квадранс нам тут не нужен. (Тут и без него птичьего языка хватает).

Вообще, термин «резистивное расстояние» тоже не выглядит удачным. Он подразумевает, что речь идет о каком-то необычном неизвестном науке расстоянии. На самом деле резистивное расстояние — это обычное евклидово расстояние. Но в аффинном пространстве. Мы используем эту его особенность далее.

А в чем, собственно, проблема?

Если мы знаем, что такое «резистивное расстояние», то почему не можем его «просто взять и посчитать» для заданного графа?

Хм. В принципе легко. Если речь о ненаправленном графе. Если бы город построил полосы в обоих направлениях, то резистивное расстояние уменьшилось бы ровно вдвое. Поскольку сопротивление обратно пропорционально проводимости, а проводимость (пропускная способность) увеличилась в два раза. А если бы добавил по две полосы в каждом направлении, то расстояние уменьшилось бы в 3 раза. Тут все достаточно тривиально. (И наверное, кто-то здесь уже может догадаться об общем виде решения. А мы едем дальше).

Когда встречные связи не равны, то все усложняется. Причем достаточно сурово.

Нет простого легального общепринятого способа определения близости вершин (резистивных расстояний) в направленном графе.

(Это мой тезис — возможно, кто-то сможет переубедить меня). «Нет» — тут означает, что его нет в учебниках, вики, и в головах (точнее — есть много разных способов от разных авторов, которые требуют разных допущений и определений). Сам-то способ есть (хотя и не такой уж простой). В данной статье мы как раз его и описываем.

Само определение расстояния при наличии направленных связей требует уточнения, если речь идет о направленном графе (некоммутативной метрике, извиняюсь). Можно говорить о расстоянии от до , а можно от до . И скорее всего данные расстояния не всегда равны. Про какие именно расстояния идет речь в задаче?

Евклидово расстояние рулит

Вынырнем и сделаем глубокий вдох. Мы уже упоминали, что резистивное расстояние является обычным евклидовым. Это означает, что его определение можно свести к определению евклидова расстояния как нормы разности двух элементов:

Данное определение не зависит от порядка элементов — это коммутативное расстояние, близость (точнее дальность) элементов. Точка в выражении означает операцию скалярного произведения (пространство метрическое). Соответственно, выражение (1) можно раскрыть:

Здесь , — нормы элементов. Когда речь идет за графы, то нормы элементов как правило равны нулю. В исходной задаче про нормы ничего не сказано, поэтому можно принять их нулевыми (подробнее про то, что означают нормы элементов в аффинном пространстве есть тут. А если еще более подробно, то тут). Тогда выражение для искомого расстояния принимает вид:

Согласно выражению (3) все, что надо для решения задачи — это найти скалярные произведения элементов (узлов) в направленном графе (легко сказать, а как это сделать?).

Попутно формула (3) показывает, что наша общая (коммутативная) мера близости между элементами и является суммой двух направленных расстояний:

— направленное расстояние от до ,
— направленное расстояние от до .

2. Решение. Долгая дорога в дюнах

Гул затих. Веселье кончилось. Дальше идут унылые подробности описания сути метода расчета скалярного произведения между узлами направленного графа. Это та часть, которую я не знаю, как рассказать «по-простому на пальцах». Но именно здесь самое важное в статье. То, ради чего стоило тратить на нее время.

Общий ход рассуждений следующий. Мы аккуратно и без эмоций новых дополнительных предположений перенесем известные свойства метрики симметричных пространств на несимметричные. Все, что нужно — это учесть особенности метрики в аффинных пространствах.

Любой связный граф (неважно — направленный или нет) задает аффинное метрическое пространство. Некоторые свойства таких пространств в симметричном (коммутативном) исполнении были (сумбурно) описаны в уже упоминавшейся серии статей или более точно и подробно в упоминавшемся лонгриде. Не спешите переключаться, — ниже приведем (правда, скороговоркой) основные выжимки.

Аффинное метрическое пространство (ненаправленный граф)

Что важно. Сначала общеизвестное.

1. Аффинность пространства означает, что понятия вектор и элемент в пространстве отличаются. Вектор — это разность элементов. Это казалось бы несущественная особенность, приводит к существенным последствиям, если в пространстве определена метрика.

2. Пространство задается базисом, состоящим элементов. Вершины графа и есть базис пространства. Связи в графе определяют его метрические свойства.

3. Характеристикой связности графа является матрица смежности. Но для метрических (и прочих) свойств более важен лапласиан графа (матрица Кирхгофа) .

4. Лапласиан графа — это почти метрический тензор. «Почти» — тут означает, что он неполон. Лапласиан является вырожденной матрицей и потому не обратим. А стандартный метрический тензор вполне себе обратим.

Теперь менее известное.

5. Различие между элементами и векторами в метрическом аффинном пространстве приводит к существованию в нем нуль-вектора . Скалярное произведение элементов с нуль-вектором в коммутативном (симметричном) пространстве равно единице (в некоммутативном зависит от направления умножения). Без нуль-вектора пространство графа не является полным! Это важно.

6. Дуальным по отношению к нуль-вектору является ортогональный центр базиса . Это такой элемент, который ортогонален всем остальным элементам базиса (кроме нуль-вектора). Напомним, что ортогональность элементов означает, что их скалярное произведение равно нулю. Ортоцентром треугольника является описанная окружность. Да, в полном аффинном пространстве элемент с ненулевой нормой — это не точка, а n-мерная сфера.

7. Лапласиан графа в совокупности с координатами ортогонального центра становится полным (полноценным метрическим тензором). Другими словами полный лапласиан — это обычный лапласиан графа , но окаймленный барицентрическими координатами ортогонального центра.

8. Обращение полного лапласиана позволяет получить полный грамиан — матрицу скалярных произведений элементов базиса (в нашем случае — вершин графа). Данный грамиан также является полноценным метрическим тензором пространства.

9. Окаймлением полного грамиана является кортеж из единиц (скалярные произведения элементов базиса и нуль-вектора). В углу — ноль, это норма самого нуль-вектора.
Известная матрица Кэли-Менгера — это почти правильный грамиан.

В итоге приходим к тому, что согласно п.8 задача определения скалярных произведений (а, значит, и расстояний) между узлами графа сводится к определению исходного метрического тензора базиса .

Нужен метод построения полного грамиана графа по заданному (неполному) лапласиану .

В случае симметричных связей построение полного грамиана по лапласиану (и наоборот) не вызывает особых затруднений. В этом случае скалярные произведения элементов базиса и нуль-вектора коммутативны — не зависят от порядка умножения:

Для направленных графов (некоммутативных пространств) задача усложняется. Хотя бы потому, что само количество возможных связей в направленном графе удваивается.

Некоммутативное аффинное пространство (направленный граф)

Про свойства лапласиана направленного графа мы тоже уже писали на хабре. Рассказывали, как можно использовать потенциалы лапласиана для ранжирования объектов. В терминах базисов потенциалы лапласиана — это дуальные координаты нуль-вектора (аннулятор лапласиана).

В данной статье нас интересуют метрические свойства. Если граф направленный, то скалярное произведение между его вершинами зависят от порядка:

Это означает, что дуальные координаты в направленных графах расщепляются (на левые и правые). Значения скалярных произведений нуль-вектора и элементов базиса (окаймление грамиана) тоже зависят от порядка множителей. И поэтому в отличие от коммутативного пространства здесь одна половина дуальных координат нуль-вектора неизвестна и подлежит определению.

Однако известных величин тоже много.

Во-первых, известен сам лапласиан. Кроме того известно, что сумма его строк равна нулю (в общем случае это необязательное требование, но для лапласианов направленных графов это обычно так). Еще важно, что барицентрические координаты элементов единственны, поскольку не зависят от метрики пространства. То есть окаймление лапласиана графа является симметричным как для направленного, так и для ненаправленного графа (именно этот пункт я не сразу осознал). Наконец, нам известны нормы элементов базиса (обычно в графах они равны нулю).

Осталось подставить все известные и неизвестные в тождество, связывающее лапласиан и грамиан:

Здесь — это тождественная матрица. В этом тождестве смысл перехода от неполного лапласиана к полному.

Заткнулись и считаем

Перейдем от слов к делу. Вот как выглядит лапласиан для графа из двух узлов:

Для простоты мы обозначили связи цифрами: . Предполагается, что значения связей известны — через них мы будем выражать все остальные величины.

Полный лапласиан включает в себя координаты ортоцентра :

Здесь — норма ортоцентра (в симметричном случае интерпретируется как квадрат радиуса), и — коэффициенты разложения ортоцентра по базису (барицентрические веса).

Полный грамиан выглядит примерно так:

Здесь кортежи и отражают дуальные координаты нуль-вектора. Данные координаты являются аннуляторами лапласиана (при умножении на лапласиан дают нулевой вектор — не путать с нуль-вектором!).

Для решения задачи нам надо найти сумму значений грамиана: .

Считаем количество неизвестных: — всего 7 (да-да, — чтобы выяснить значение одного несчастного расстояния, нам надо рассчитать еще семь дополнительных величин). На входе есть две известных связи — и . Тождество даст 9 уравнений. Итого 7+2 = 9, — все сходится (удивительно). Осталось просто решить систему уравнений.

Для графа из двух узлов решение (все неизвестные) можно выразить в явном виде. Приведем конечные выражения для интересующих нас величин. Введем понятие общей геометрической связности — это величина, обратная норме ортогонального центра . Ее размерность совпадает с размерностью связей графа. Для графа из двух узлов (и двух связей) геометрическая связность имеет симпатичное выражение:

Через данную связность можно выразить скалярные произведения узлов:

Можно перевести скалярные произведения в направленные расстояния (3):

Искомое коммутативное расстояние между узлами определяется суммой:

Бабушка приехала

Наконец-то. Выражение (4) — это и есть искомая формула.

Расстояние между вершинами графа из двух узлов обратно пропорционально квадратному корню из произведения встречных связей.

Можно нагрузить школьный учебник еще одной бесполезной формулой.

Если связи равны, то результат совпадает с резистивным расстоянием в ненаправленных графах:

Посчитаем, что там с нашим городком. Если проложить вторую полосу, то связь в одном направлении увеличится в два раза. Соответственно, новое расстояние можно выразить в терминах исходного:

Расстояние между районами уменьшится в раз. Это же было очевидно, да?

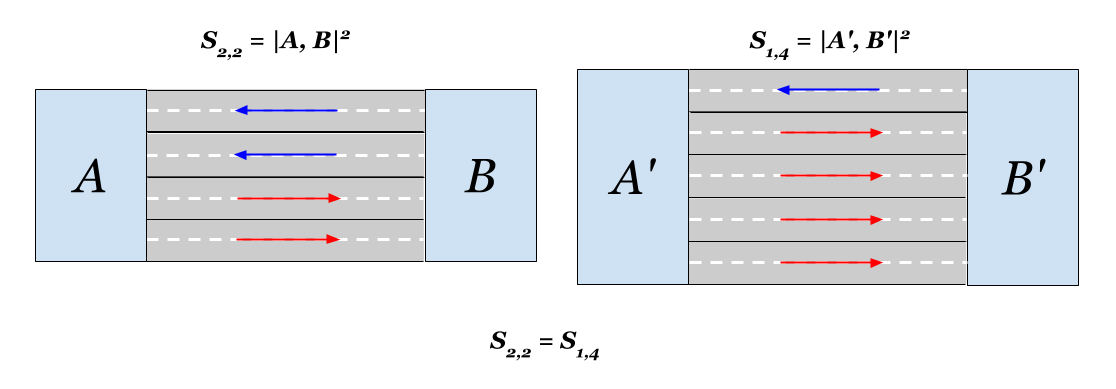
Получается также, что с точки зрения расстояний добавление к двухполосной дороге по одной полосе с каждой стороны эквивалентно добавлению трех полос с одной. Евклидова близость в обоих случаях увеличится в два раза. Занятно.

На этом все. Спасибо за внимательность ).

Приложение. Явные выражения для остальных элементов матриц нашего графа

Координаты ортоцентра:

Скалярные произведения базиса и нуль-вектора (аннулятор лапласиана):

Автор: dmagin

Источник