Быстрая, экономная, устойчивая…

Если вам понадобится алгоритм сортировки массива, который:

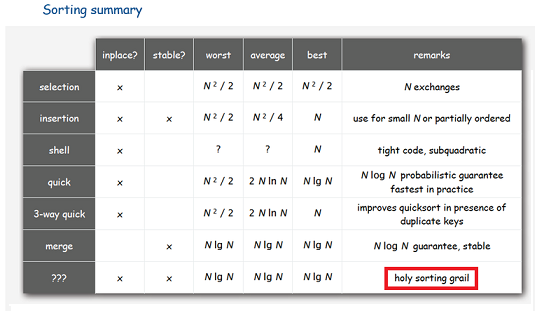
• Работал бы гарантированно за O(N*log(N)) операций (обменов и сравнений);
• Требовал бы O(1) дополнительной памяти;
• Был бы устойчивым (то есть, не менял порядок элементов с одинаковыми ключами)

то вам, скорее всего, предложат ограничиться любыми двумя из этих трёх пунктов. И, в зависимости от вашего выбора, вы получите, например, либо сортировку слиянием (требует O(N) дополнительной памяти), либо пирамидальную сортировку (неустойчив), либо сортировку пузырьком (работает за O(N²)). Если вы ослабите требование на память до O(log(N)) («на рекурсию»), то для вас найдётся алгоритм со сложностью O(N*(log(N)²) — довольно малоизвестный, хотя именно его версия используется в реализации метода std::stable_sort().

На вопрос, можно ли добиться выполнения одновременно всех трёх условий, большинство скажет «вряд ли». Википедия о таких алгоритмах не знает. Среди программистов ходят слухи, что вроде бы, что-то такое существует. Некоторые говорят, что есть «устойчивая быстрая сортировка» — но у той реализации, которую я видел, сложность была всё те же O(N*(log(N)²) (по таймеру). И только в одном обсуждении на StackOverflow дали ссылку на статью B-C. Huang и M. A. Langston, Fast Stable Merging and Sorting in Constant Extra Space (1989-1992), в которой описан именно такой алгоритм.

Авторы говорят, что их алгоритм не первый, и ссылаются на работу L. Trabb Pardo, Stable sorting and merging with optimal space and time bounds 1974 года. Это около 80 страниц отсканированного текста, и разобраться в нём я не пытался.

Сразу скажу для тех, кто попробует разобраться в статье Huang и Langston, что реализовать алгоритм в том виде, в каком он там описан, мне не удалось. Приём, который они используют в пункте 4.3, не работает, потому что утверждение «That is, it directly follows that the head of the rightmost block of a second-sublist series will temporarily have a key strictly greater than that of the record to its immediate right» верно не всегда. К счастью, в некоторых более поздних работах удалось найти способ, позволяющий обойти эту неприятность, и теперь я могу сказать, что алгоритм, удовлетворяющий всем трём условиям, действительно существует.

Итак, начнём...

Основные операции

Для работы с массивом нам понадобятся функции:

• SWAP1(A,B) — обменять местами два элемента. Сложность равна 1.
• SWAPN(A,B,K) — обменять местами K пар элементов массивов A и B. Сложность равна K.
• ROTATE(A,K,L) — переставить два подряд идущих фрагмента массива A, длина первого равна K, длина второго — L. Сложность не превосходит K+L.
• BinSearchLeft(X,A,L) — найти самое левое место для вставки элемента X в упорядоченный массив A длины L. Допустимые значения результата — от 0 до L. Сложность — log(L).
• BinSearchRight(X,A,L) — найти самое правое место для вставки элемента X в упорядоченный массив A длины L. Допустимые значения результата — от 0 до L. Сложность — log(L).

Ищем буфер для обмена.

Сначала немного терминологии.
Про элементы, для которых функция сравнения выдала результат, что они равны, будем говорить, что «у них совпадают ключи», хотя физически никаких ключей может не существовать. Соответственно, можно определить число различных ключей в массиве и элементы с различными ключами.

Два состояния массива будем называть эквивалентными, если элементы с одинаковыми ключами в них находятся в одинаковом порядке. Главная проблема устойчивых in-place сортировок — не потерять эту эквивалентность, или всегда уметь её восстановить.

Пусть длина массива равна N. Если N<16, то такой массив мы сортировать не будем, а вызовем вместо этого сортировку вставками — на общую асимптотику это не повлияет.

Выберем число S, равное степени двойки, близкое к sqrt(N). Определим K=[N/S]. И попробуем найти в массиве K+S попарно различных ключей.

Первая идея заключается в том, что если мы возьмём для каждого ключа самый левый элемент массива с этим ключом, и соберём все такие элементы в начале массива (сохранив порядок остальных элементов), то эквивалентность не нарушится, но это даст нам пространство, в котором мы можем свободно переставлять и сравнивать друг с другом элементы.

В процессе поиска мы будем держать найденные ключи в непрерывном фрагменте массива, и двигать его вперёд по мере нахождения новых ключей: перебирая элементы массива, будем бинарным поиском искать их в фрагменте найденных ключей, и если не нашли — то за одну операцию ROTATE подгоняем массив с ключами к найденному элементу, а за вторую — ставим новый элемент на нужное место в этом фрагменте.

Ключи собираются в порядке возрастания, что позволяет экономить время на проверку, встретился ли нам уже элемент с таким же ключом, что и у текущего элемента. Число перемещений фрагмента с ключами не больше числа найденных ключей, так что сложность этого этапа составляет, в худшем случае, N*log(NKeys) сравнений и 2*N+NKeys² обменов. Поскольку NKeys у нас порядка 2*sqrt(N), то пока мы за границу не вышли.

Теперь у нас есть два варианта. Либо мы нашли заказанные K+S ключей, либо не нашли. Эти случаи обрабатываются слегка по-разному. Кроме того, есть случай, когда число различных ключей меньше 4 — для него тоже есть своя обработка.

Случай A. Различных ключей много.

У нас есть K+S различных ключей, собранных в начале массива. Первые K из них мы объявим «ключами для маркировки фрагментов» и пока трогать не будем. Остальные S будут буфером для слияния. Все оставшиеся элементы исходного массива — «данными», сейчас они лежат в конце массива.

A.1. Этап классической сортировки слиянием.

Напишем ещё две функции. Одна будет называться MergeLeft, другая MergeRight. Им подаются на вход фрагменты массивов, состоящие из трёх частей. В случае MergeLeft это буфер длины P, отсортированный фрагмент длины Q и отсортированный фрагмент длины R, где S≥R. Функция должна слить второй и третий фрагменты, положить результат в начало, а элементы буфера в произвольном порядке в конец данного фрагмента. Функция MergeRight работает зеркально — на входе у неё два отсортированных фрагмента, а за ними буфер, а на выходе — наоборот, буфер, а за ним отсортированный фрагмент. Выглядит это примерно так:

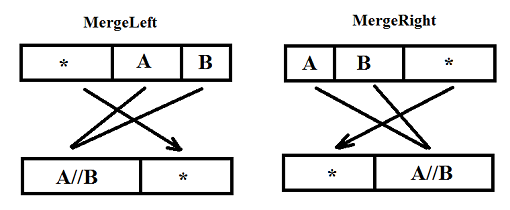
Сложность обеих функций не превосходит Q+R — как по сравнениям, так и по обменам.
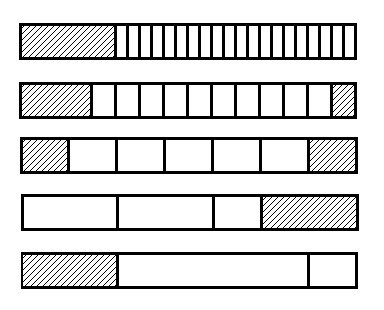
Пользуясь функцией MergeLeft, мы можем отсортировать данные сначала по парам, потом по четвёркам,… вплоть до фрагментов длины S (напомню, что S — степень двойки). Каждый раз при сортировке M элементов мы используем кусочек буфера длины M/2, который в результате уезжает в правую часть массива. На этапе сортировки пар мы воспользуемся кусочком буфера длины 2, так что в итоге к моменту, когда отсортированные куски будут длины S, массив данных у нас окажется прижатым влево, а S элементов буфера будут справа. Теперь мы можем использовать MergeRight, отсортировать фрагменты длиной 2*S, и заодно, вернуть буфер в начало.

A.2. Этап блочной сортировки.

Сейчас у нас отсортированы фрагменты длиной G=2*S. Мы будем сливать их попарно, потом ещё раз попарно и т.д., пока не достигнем размера всего массива данных. Для этого у нас есть буфер длиной S и массив с ключами длиной K, где K ≤ L/S (L — полная длина массива данных).
Итак, цикл «пока G ≤ L».

Мы хотим слить два подряд идущих фрагмента длины G, причём непосредственно перед ними находится буфер длины S (G и S — степени двойки). Делим наши фрагменты на блоки длины S. Пусть их получилось K₁. Второй фрагмент в самом конце массива мог иметь длину меньше G, и после деления от него может остаться неполный блок, его мы тоже посчитаем (хотя двигать не будем). Возьмём первые K₁ ключей (они лежат в начале исходного массива), отсортируем их (например, вставками) и запомним индекс ключа с номером G/S (сейчас он равен G/S, но потом будет меняться) — назовём его midkey. Каждому ключу соответствует свой блок. Мы их используем, во-первых, чтобы различить первый и второй сливаемые фрагменты, а во-вторых, чтобы поддержать порядок блоков с одинаковыми элементами. Потому что сейчас мы их будем перемешивать как попало.

Отсортируем блоки. Порядок будет определяться первыми элементами, а если они равны — то соответствующими этим блокам ключами. Единственная сортировка, которой мы можем здесь воспользоваться — это сортировка выбором минимального элемента, поскольку она требует не более K₁ обмена (и K₁²/2 сравнений): обмен двух блоков это дорогая процедура, но, поскольку S это примерно sqrt(N), то весь этап сортировки укладывается в O(N) операций. Когда мы переставляем два блока, то переставим и соответствующие им ключи, не забывая следить за ключом midkey. Неполный блок (если он есть) при этой сортировке мы не трогаем!

Блоки, ранее принадлежавшие первому фрагменту, мы будем обозначать буквой A, а блоки, принадлежавшие второму — буквой B. При нашей сортировке порядок блоков, соответствовавших каждому фрагменту,
сохранился.

Неполный блок всегда принадлежит фрагменту B. Просмотрим блоки, идущие перед ним, чтобы узнать, перед каким блоком его следовало бы вставить. Возможно, что его придётся вставить в самое начало, или оставить на месте — в алгоритме на эти случаи нужно обратить особое внимание. На следующем этапе трогать блоки, которые следовало бы подвинуть (все они из фрагмента A), мы пока не будем.

Теперь начнём сливать блоки. Ситуация в каждый момент у нас будет такой:

• Сначала идёт некоторое количество полных слитых блоков, про которые известно, что мы их больше не трогаем.
• Потом несколько (T, возможно, T=0) элементов следующего блока, которые тоже уже на месте.
• Потом S элементов буфера
• Потом S-T элементов, место для которых ещё не определено. Все они принадлежат одному фрагменту — A или B, и мы знаем, какому.
• Дальше идут необработанные блоки, тип которых мы можем определить, сравнив соответствующий им ключ с midkey.

Выглядит это примерно так:

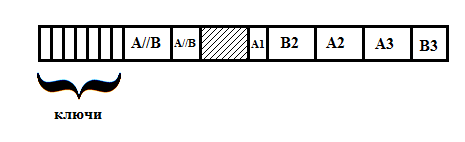
Здесь A//B — отсортированный участок, A1 — недообработанный блок, A2,A3,B2 — необработанные блоки, B3 — неполный блок в конце (возможно, его настоящее место перед A2 или A3).
В начале у нас слитых блоков нет, T=0, а тип S-T элементов, идущих после буфера, определяется по первому ключу.

Чтобы обработать очередной блок, нам придётся написать ещё одну функцию SmartMergeLeft (и она не последняя!). На вход ей, как и MergeLeft, подаются буфер и два фрагмента, причём порядок этих фрагментов может быть неправильным (тогда при слиянии надо будет в случае равных элементов брать элемент из второго фрагмента). Функция должна переставлять элементы в начало только до тех пор, пока оба фрагмента непусты. Как только один из них кончится, она должна перенести оставшиеся элементы другого фрагмента в конец (если второй фрагмент кончился раньше), сообщить их число, и то, в каком фрагменте они были.
Примерно так:

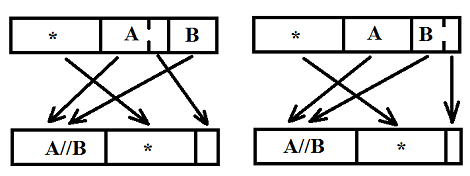
В первом случае сначала кончились элементы из B, и в конце остались последние элементы из A, а во втором — наоборот.
Пользуясь этой функцией, мы легко можем продвинуться на один блок. Если тип следующего блока такой же, как у последних необработанных элементов, мы меняем их с буфером, и говорим, что T=0, а необработанным является новый блок (ситуация такая же, как в начале). Если типы разные, вызываем SmartMergeLeft, и она всё делает сама — элементы, которые останутся в конце блока, и будут необработанными.

Так, перебирая блоки, мы дойдём либо до конца, либо до того места, где должен стоять неполный блок из конца фрагмента B. Здесь у нас несколько вариантов.

Либо последние оставшиеся необработанные элементы — из фрагмента B. Тогда последний из этих элементов меньше, чем первый элемент из следующего за ним блока A (если такой есть), и мы можем смело обменять необработанные элементы с буфером.

Либо эти элементы из фрагмента A. Тогда мы просто виртуально приклеиваем их к следующим за ними блокам (опять же, если они есть).
В обоих случаях получаем одну и ту же ситуацию — буфер, за ним элементы из фрагмента A, потом — не более, чем S элементов из фрагмента B. Готовая ситуация для функции MergeLeft. Вызываем её — и фрагменты слиты, причём буфер оказался после них.

Проходим этой процедурой по всем парам фрагментов длины G, пока не дойдём до конца массива данных. После чего сдвигаем все данные вправо на S элементов (возвращая буфер в начало), и удваиваем значение S.
Конец цикла.

A.3. Завершение.

У нас получился отсортированный массив данных, перед которыми идут в случайном порядке найденные в начале ключи. Отсортируем их (опять вставками), и нам останется слить два отсортированных фрагмента без использования дополнительного буфера. На этот раз нас спасёт то, что один из них очень короткий.

Функция MergeWithoutBuffer получает на вход два отсортированных фрагмента длины P и Q. Предположим, что P<Q. Пока первый элемент первого фрагмента не больше первого элемента второго фрагмента, будем уменьшать P на 1, сдвигая начало фрагмента вправо. Если P достигнет нуля — мы победили. Иначе найдём с помощью BinSearchLeft правильное положение k первого элемента во втором фрагменте, и с помощью ROTATE поменяем первый фрагмент и первые k элементов второго фрагмента. Уменьшим Q на k, сдвинем начало фрагментов. Если Q достигло нуля — функция выполнена, иначе повторяем её с начала. Сложность этой функции — P^2+Q. Если исходно было P≥Q, то делаем то же, но в зеркальном порядке.

Для завершения сортировки вызываем MergeWithoutBuffer(Arr,K+S,N-K-S). Всё готово.

Случай B. Различных ключей мало, но больше трёх.

В этой ситуации места на буфер и на ключи одновременно у нас нет, будем использовать их по очереди. Пусть различных ключей всего M. Обозначим через K максимальную степень двойки, не превосходящую M, и оставим себе K ключей (они в начале массива), остальное пустим на данные.

B.1. Этап классической сортировки слиянием.

Этот этап не отличается от A.1, только вместо буфера длиной S мы будем использовать массив ключей длиной K (это степень двойки). Прогулявшись по массиву вперёд и назад, получим отсортированные фрагменты длиной G=2*K.

B.2. Этап блочной сортировки.

Допустим, что фрагменты длиной G у нас уже слиты, и мы хотим объединить их попарно. Поскольку буфера у нас нет, мы можем сами выбрать размер блока. Число ключей для разметки блоков у нас не превосходит K. Возьмём K₁=min(K,K₂), где K₂ — степень двойки, ближайшая к (2*G*M)^1/3 (напомним, что M — число различных ключей в массиве). Размером блока у нас будет S=2*G/K₁.

Сортируем ключи и блоки так же, как в A.2. Для этого буфера не нужно.
Теперь нам нужно пройтись по массиву и слить блоки. Напишем функцию SmartMergeWithoutBuffer, являющуюся гибридом MergeWithoutBuffer и SmartMergeLeft. В ней предполагается, что первый фрагмент короче второго. Она работает так же, как MergeWithoutBuffer, но учитывает, что порядок фрагментов мог быть неправильным, а кроме того, сообщает, сколько элементов и из какого фрагмента остались в конце массива. Вызывая эту функцию вместо SmartMergeLeft, а функцию MergeWithoutBuffer — вместо MergeLeft в конце, получим слитые фрагменты.

Казалось бы, здесь мы и проиграли — максимальная длина блока в худшем случае (K=4,G=N/2) равна N/4, а значит, функции SmartMergeWithoutBuffer может потребоваться O(N^2) операций. Но нас спасает то, что число различных ключей в массиве мало — и можно показать, что сложность SmartMergeWithoutBuffer не превосходит P*m+Q, где m — число различных ключей в первом фрагменте. А поскольку сумма числа различных ключей по всем K/2 блокам фрагмента длины G (сделайте глубокий вдох и перечитайте — проще я сформулировать не могу) не превосходит K/2+M, то на слияние двух фрагментов длины G потратится не более O(G) операций.

B.3. Завершение.

Этот этап не отличается от A.3.

Случай C. Различных ключей не больше трёх.

Здесь мы пишем обычную сортировку слиянием (без рекурсии — сортируем по 2, потом по 4 элемента и т.д.), а для слияния фрагментов используем MergeWithoutBuffers. Поскольку различных ключей в массиве мало, её сложность будет линейной от длины сливаемых фрагментов, а значит, общая сложность — O(N*log(N)).

Реализация и выводы.

Реализация получилась громоздкой — почти 400 строк на C++. Скорость работы сильно различается для случаев A и B. Хуже всего ситуация, когда различных ключей много, но чуть-чуть меньше, чем нужно для перехода к случаю A — в этой ситуации алгоритм работает медленнее, чем в случае A, примерно в 3 раза. Тем не менее, оценка сложности N*log(N) сохраняется.

На больших массивах (примерно от 10 миллионов) алгоритм почти всегда (кроме случаев совсем уж маленького числа различных ключей) обыгрывает InPlaceStableSort (тот, который за O(N*log(N)²)). Но тягаться с std::stable_sort он не в силах: хоть немного памяти найдётся всегда, а в этом случае std::stable_sort быстро переключается на обычный MergeSort, и легко и непринуждённо обгоняет всех, включая quicksort :). Так что реализованный алгоритм имеет лишь теоретическое значение.

Но всё-таки, он существует :)

Автор: Mrrl

Источник