
Эпизод с основанием Microsoft – один из наиболее известных в компьютерной истории. В 1975 году Пол Аллен вылетел в Альбукерк, чтобы продемонстрировать интерпретатор BASIC, которые они с Биллом Гейтсом написали для микрокомпьютера Altair. Поскольку у них не было работающего компьютера Altair, они проверили свой интерпретатор при помощи написанного ими эмулятора, выполнявшегося на компьютерной системе Гарварда. Эмулятор был основан только на опубликованных спецификациях процессора Intel 8080. Когда Аллен, наконец, запустил интерпретатор на реальном компьютере Altair – перед человеком, который, как они надеялись, купит их ПО – он даже не знал, заработает ли программа. Она заработала. В следующем месяце Аллен и Гейтс официально основали новую компанию.
За более чем сто лет до интерпретатора BASIC Аллена и Гейтса, Ада Лавлейс написала и опубликовала компьютерную программу. Она тоже написала программу для компьютера, о котором знала только по описанию. Но её программа, в отличие от интерпретатора BASIC, никогда не выполнялась, потому что компьютер, для которого она была написана, так и не был построен.
Программу Лавлейс часто называют первой в мире компьютерной программой. Но не все согласны с тем, что её следует так называть. Наследие Лавлейс оказывается одной из самых горячо обсуждаемых тем компьютерной истории. Уолтер Айзексон писал, что диспут по поводу степени и достоинств её вкладов представляет «небольшую академическую важность». С неизбежностью диспут подогревает тот факт, что Лавлейс была женщиной. Историки цитировали всякого рода свидетельства, чтобы доказать, что оказываемые ей почести соответствуют случаю, или, наоборот, незаслуженны. Но они тратят гораздо меньше времени на объяснение технических деталей её опубликованной работы, что обидно, поскольку именно технические детали представляют самую интересную часть этой истории. Кому же неинтересно было бы узнать, как должна была работать программа, написанная в 1843 году?
Честно говоря, программу Лавлейс тяжело объяснить обывателям. Но именно запутанность её программы делает её такой примечательной. Достойна она зваться первым программистом, или нет, её программа была записана с такой точностью, которая превзошла всё, что было до этого. Она тщательно продумала, какие операции можно объединить в группы, которые можно будет повторять – изобретя, таким образом, цикл. Она поняла, как важно отслеживать состояние изменяющихся переменных, и придумала запись, отражающую эти изменения. Я, как программист, поражён тем, насколько работа Лавлейс напоминает опыт написания софта сегодня.
Так давайте же поближе познакомимся с программой Лавлейс. Она разработала её для подсчёта чисел Бернулли. Чтобы понять, что это такое, необходимо вернуться на пару тысячелетий в прошлое, к началу одной из наиболее старых задач математики.
Суммы степеней
Пифагорейцы жили на берегах Средиземного моря и поклонялись числам. Одним из их хобби было составление треугольников из гальки.
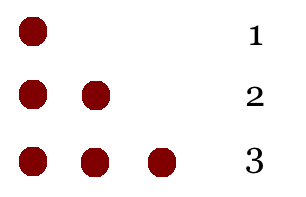
Один камень, за которым идёт ряд из двух камней, вместе составляют треугольник из трёх камней. Добавьте ещё один ряд из трёх камней, и получится треугольник из шести камней. Эту процедуру можно продолжать, каждый раз добавляя ряд с количеством камней, увеличивающимся на единицу. Треугольник из шести рядов содержит 21 камень. А сколько камней будет в треугольнике из 423 рядов?
Пифагорейцы искали способ подсчитать сумму следующего ряда, не проводя суммирование:
1+2+3+⋯+n
В итоге они поняли, что если расположить два треугольника одинакового размера рядом друг с другом так, чтобы они образовали прямоугольник, можно найти площадь прямоугольника и разделить её на два, чтобы получить количество камней в каждом из треугольников:
1+2+3+⋯+n = n(n+1)/2
Архимед изучал схожую проблему. Его интересовала следующая последовательность:
12+22+32+⋯+n2
Её можно представить себе, как столбик из квадратов всё большего размера (состоящих из крохотных кубиков), стоящих один на другом в виде пирамиды. Архимед хотел узнать, есть ли лёгкий способ сказать, сколько кубиков потребуется для создания пирамиды с, допустим, 423 уровнями. Он записал решение задачи, которое тоже допускает геометрическую интерпретацию.
Три пирамидки можно составить вместе, чтобы они сформировали прямоугольную призму, с одного конца которого есть небольшой выступ в один кубик высотой. Этот выступ представляет собой треугольник, подчиняющийся тем же правилам, что и каменные треугольники пифагорейцев. Поэтому объём всей фигуры задаётся следующим уравнением:
3(12+22+32+⋯+n2) = (n+1)n2+(1+2+3+⋯+n)
Подставляя уравнение пифагорейцев для суммы первых n целых чисел, и проведя некоторые алгебраические операции, получим:
12+22+32+⋯+n2=n(n+1)(2n+1)/6
В 499 году индийский математик и астроном Ариабхата опубликовал свою работу, известную, как Ариабхатия, в которой была приведена формула для вычисления суммы кубов:
13+23+33+⋯+n3=(1+2+3+⋯+n)2
Формулу для суммы первых n положительных целых чисел в четвёртой степени опубликовали только 500 лет спустя.
К этому времени у вас мог появиться вопрос – а нет ли какого-нибудь универсального метода для вычисления суммы первых n целых чисел, возведённых в степень k? Математики тоже этим интересовались. Йохан Фаульхабер, немецкий математик, слегка подвинутый на нумерологии, смог вывести формулы для суммы целых вплоть до 17-й степени, опубликовав их в 1631 году. Но это заняло у него много лет, и общего решения он не дал. Блез Паскаль, наконец, придумал обобщённый метод в 1665 году, который, правда, зависел от подсчёта суммы целых чисел, возведённых в предыдущие степени. К примеру, для подсчёта суммы первых n положительных целых чисел, возведённых в 6-ю степень, вам нужно было сначала узнать, как подсчитать сумму первых n положительных целых чисел, возведённых в 5-ю степень
Более практичное обобщённое решение было приведено в посмертно опубликованной работе швейцарского математика Якоба Бернулли, умершего в 1705. Бернулли начал с того, что вывел формулы для подсчёта сумм первых n положительных целых чисел, возведённых в первую, вторую, третью и четвёртую степени. Он записал их в виде многочленов:
1+2+3+⋯+n = 1/2n2+1/2n
12+22+32+⋯+n2=1/3n3+1/2n2+1/6n
13+23+33+⋯+n3=1/4n4+1/2n3+1/4n2
Используя треугольник Паскаля, Бернулли понял, что эти многочлены следуют предсказуемой закономерности. По сути, Бернулли разбил коэффициенты каждого члена на два множителя, один из которых он мог определить при помощи треугольника Паскаля, а другой – вывести из интересного свойства, по которому все коэффициенты в многочлене в сумме равнялись единице. Понять, какую экспоненту поставить у каждого члена, было несложно, поскольку они тоже следовали предсказуемой закономерности. Множители каждого коэффициента, которые нужно было вычислять по правилу «сумма равна единице», сформировали последовательность, которая стали известна, как числа Бернулли.
Открытие Бернулли не означало, что сумму первых n положительных целых чисел, возведённых в любую степень, теперь можно было вычислить тривиально. Чтобы подсчитать сумму первых n положительных целых чисел, возведённых в степень k, необходимо было узнать все числа Бернулли вплоть до k-того. А каждое число Бернулли можно было подсчитать, только зная все предыдущие. Но высчитывать длинную последовательность чисел Бернулли было несравненно легче, чем подсчитывать каждую сумму возведённых в степень чисел, поэтому открытие Бернулли стало большим прорывом для математики.
Бэббидж
Чарлз Бэббидж родился в 1791 году, почти через сто лет после смерти Бернулли. У меня всегда было такое представление о нём, что он разработал, но не построил механический компьютер. Но я никогда точно не понимал, как этот компьютер должен был работать. Как оказалось, основные идеи понять довольно легко. Программа Лавлейс должна была работать на одной из машин Бэббиджа, поэтому нам надо сделать ещё одно небольшое отступление и поговорить о том, как эти машины работали.
Бэббидж придумал две отдельных механических вычислительных машины. Первая называлась разностной машиной. До изобретения карманных калькуляторов, люди полагались на логарифмические таблицы для подсчёта произведения больших чисел. Большие логарифмические таблицы принципиально не так уж сложно составить, но количество вычислений, требовавшееся для их составления, приводило к тому, что во времена Бэббиджа в них часто содержались ошибки. Раздражённый этим, Бэббидж решил создать машину, способную механически создавать таблицы логарифмов, не допуская ошибок.
Разностная машина была не компьютером, потому что она умела только складывать и вычитать. Она пользовалась методом, придуманным французским математиком Гаспаром де Прони, разбившим процесс построения таблицы на мелкие шаги. Эти шаги требовали только сложения и вычитания, что означало, что для построения таблицы можно задействовать небольшую армию людей, не обладавших способностями к математике. Метод де Прони, известный, как метод разделённых разностей, можно было использовать для составления таблицы по любому многочлену. А многочлены уже можно было использовать для приближённого вычисления логарифмических и тригонометрических функций.
Чтобы представить себе, как работал этот процесс, рассмотрим следующую простую полиномиальную функцию:
y = x2+1
Метод разделённых разностей находит разницу между последовательными значениями y для разных значений x. Затем находятся разницы между этими разностями, и затем, возможно, ещё разницы между последними разностями, до тех пор, пока не появляется постоянная разность. Эту разность затем можно использовать для получения следующего значения полинома через сложение.
Поскольку указанный многочлен имеет лишь вторую степень, мы можем найти постоянную разность после всего лишь двух столбцов разностей:
| x | y | Diff 1 | Diff 2 |
|---|---|---|---|
| 1 | 2 | ||
| 2 | 5 | 3 | |
| 3 | 10 | 5 | 2 |
| 4 | 17 | 7 | 2 |
| 5 | ? | ? | 2 |
| … | … | … | … |
Теперь, зная, что постоянная разность равна 2, мы можем найти значение y, когда x равно 5, при помощи одного сложения. Сложив 2 и 7, последнее значение в столбце Diff 1, мы получим 9. Сложив 9 и 17, последнее значение в столбце y, мы получим 26 – наш ответ.
У разностной машины Бэббиджа для каждого разностного столбца таблицы был свой физический столбец с шестерёнками. Каждая шестерёнка представляла десятичную позицию, а весь столбец – десятичное число. У разностной машины было восемь колонок с шестернями, поэтому она могла составлять таблицы полиномов вплоть до седьмой степени. Колонки изначально ставили на значения, совпадающие с ранним рядом таблицы разностей, просчитанным заранее. Оператор затем должен был поворачивать коленчатый вал, что заставляло постоянную разность перемещаться по машине, когда значения, хранившиеся в каждой из колонок, добавлялись к следующим.
Бэббидж сумел построить небольшую часть разностной машины и использовать её для демонстрации своих идей на вечеринках. Но, даже потратив столько денег, что их хватило бы на постройку двух крупных боевых кораблей, он так и не смог завершить свою машину. В начале XVIII века Бэббидж не нашёл никого, кто смог бы изготовить нужное ему количество шестерней с нужной точностью. Рабочую версию разностной машины построили лишь в 1990-х годах, после появления высокоточных станков.
В итоге Бэббидж потерял интерес к разностной машине, поняв, что можно создать куда как более мощную и гибкую машину. Его "аналитическая машина" сегодня известно, как механический компьютер Бэббиджа. Аналитическая машина основывалась на тех же колонках шестерней, что и разностная, но если у последней было всего восемь колонок, то у аналитической их должно было быть несколько сотен. Аналитическую машину можно было бы программировать при помощи перфокарт, как жаккардовый ткацкий станок, и она могла бы делить и умножать, а не только складывать и вычитать. Для выполнения одной из этих операций часть машины под названием «мельница» перестраивала бы себя в нужную конфигурацию, считывала бы операнды с других колонок, использовавшихся для хранения данных, а потом писала бы результат на другие колонки.
Бэббидж назвал её аналитической машиной, поскольку она была достаточно мощной для того, чтобы заниматься чем-то, напоминающим матанализ. Разностная машина могла выдавать таблицы полиномов, но аналитическая машина могла бы подсчитать, к примеру, коэффициенты полиномиального размножения другого выражения. Это была удивительная машина, но британское правительство приняло мудрое решение отклонить запрос на её финансирование. Поэтому Бэббидж направился за границу, в Италию, чтобы там попробовать найти себе поддержку.
Примечания переводчицы
В Турине Бэббидж познакомился с итальянским инженером и будущим премьер-министром Луиджи Федерико Менабреа. Он убедил Менабреа написать обзор возможностей аналитической машины. В 1842 Менабреа опубликовал работу по этой теме на французском языке. В следующем году Лавлейс опубликовала перевод работы Менабреа на английский.
Лавлейс, известная тогда, как Ада Байрон, познакомилась с Бэббиджем на вечеринке в 1833 году, когда ей было 17, а ему 41. Лавлейс была поражена разностной машиной Бэббиджа. Но она смогла разобраться, как та работает, поскольку в детстве её активно обучали математике. Её мать, Анабелла Милбанк, решила, что твёрдая математическая основа образования дочки отвадит от неё дикую и романтическую натуру, которой обладал её отец лорд Байрон, знаменитый поэт. После знакомства в 1833 году Лавлейс и Бэббидж оставались в общем социальном кругу и часто переписывались.
Ада Байрон вышла замуж за Уильяма Кинга в 1835. Кинг позднее стал графом Лавлейсом, вследствие чего Ада стала графиней Лавлейс. И даже родив троих детей, она продолжала обучаться математике, взяв в учителя Огастеса де Моргана, открывшего законы Моргана. Лавлейс сразу распознала потенциал аналитической машины, и с готовностью согласилась работать с ним для продвижения этой идеи. Её друг предложил ей перевести работу Менабреа для английской аудитории.
В работе содержалось краткое описание работы разностной машины, а потом было показано, насколько бы её превзошла аналитическая машина. Аналитическая машина должна была быть настолько мощной, что могла бы «сформировать результат перемножения двух чисел, каждое из которых состоит из двадцати знаков, всего за три минуты». Менабреа дал и другие примеры возможности машины, демонстрируя, как она решала бы простую систему линейных уравнений и раскладывала бы результат перемножения двух биномов. В обоих случаях Менабреа представил то, что Лавлейс назвала «диаграммами развития», описывавшими последовательность операций, необходимых для вычисления правильного ответа. Это были программы, в том же смысле, в каком программа Лавлейс была программой, и они были опубликованы за год до её работы. Но, как мы увидим, программы Менабреа были всего лишь примерами возможного. Все они были тривиальными в том смысле, что не требовали никакого разветвления или циклов.
Лавлейс добавила несколько примечаний к своему переводу работы Менабреа, и в сумме они оказались длиннее оригинальной работы. Именно там она сделала свой основной вклад в вычисления. В примечании А, которое Лавлейс сделала к изначальному описанию аналитической машины, она подробно, и иногда лирически объясняла, что эта машина сможет выполнять произвольные математические операции. Она предвидела, что машина, подобная этой, не будет ограничена работой с числами, и сможет обрабатывать любые объекты, «чьё взаимное фундаментальное взаимодействие можно выразить абстрактной наукой операций, и которые можно приспособить к операционным записям и механизму машины». Она добавила, что когда-нибудь такая машина сможет, например, сочинять музыку. Такое предвидение было тем более примечательно, что сам Менабреа считал эту машину лишь инструментом для автоматизации «длительных и скучных вычислений», который бы освободил интеллектуальные возможности гениальных учёных для более передовых исследований. Чудесное предвидение Лавлейс, продемонстрированное в примечании А, является одной из главных причин того, почему мы чествуем её сегодня.
Другое знаменитое примечание – примечание G. Лавлейс начинает его, утверждая, что, несмотря на впечатляющие возможности, нельзя сказать, что аналитическая машина «думает». Именно это примечание Алан Тьюринг позже будет называть «возражением Ады Лавлейс». Тем не менее, продолжает Лавлейс, машина способна на удивительные вещи. Для демонстрации возможности обработки более сложных задач, Лавлейс предлагала свою программу для вычисления чисел Бернулли.
Полный её текст, в виде расширенной «диаграммы развития», формат которой Лавлейс описывает в примечании D, можно посмотреть тут. Это, по сути, список операций, обозначенных математическими символами. Не похоже, чтобы Бэббидж или Лавлейс зашли так далеко, чтобы разработать набор операционных кодов для аналитической машины.
Хотя Лавлейс описывала метод вычисления полной последовательности чисел Бернулли до определенного предела, приведённая ею программа показывала только один шаг этого процесса. Она подсчитывала число, которое она назвала B7, известное современным математикам, как восьмое число Бернулли. Поэтому её программа решала следующее уравнение:
B7=−1(A0+B1A1+B3A3+B5A5)
Тут каждый член представляет коэффициент в полиномиальной формуле для суммы целых чисел, возведённых в определённую степень. Тут речь идёт о восьмой степени, поскольку восьмое число Бернулли впервые появляется в формуле для суммы целых положительных чисел, возведённых в восьмую степень. Числа B и A представляют два вида множителей, открытых Бернулли. Числа от B1 до B7 – различные числа Бернулли, пронумерованные согласно Лавлейс. Числа от A0 до A5 представляют собой множители коэффициентов, которые Бернулли мог вычислить при помощи треугольника Паскаля. Значения A0, A1 и A3 приведены ниже. Здесь n обозначает индекс чесла Бернулли в последовательности нечётных чисел Бернулли, начинающихся с первого. В программе Лавлейс n = 4.
A0=−1/2⋅(2n−1)/(2n+1)
A1=2n/2
A3=2n(2n−1)(2n−2)/(2⋅3⋅4)
A5=2n(2n−1)(2n−2)(2n−3)(2n−4)/(2⋅3⋅4⋅5⋅6)
Я перевёл программу Лавлейс на язык C, и так, наверное, её будет проще читать. Сначала её программа вычисляет A0 и результат умножения B1A1. Затем начинается цикл, повторяющийся дважды, для вычисления B3A3 и B5A5, поскольку они считаются по одной схеме. После подсчёта каждого перемножения, результат добавляется к предыдущим, поэтому к концу программы получается полная сумма.
Очевидно, что перевод на C не может быть точным воспроизведением программы Лавлейс. Он объявляет переменные в стеке, а переменные Лавлейс больше были похожи на регистры. Но он делает более очевидной наиболее пророческую часть программы Лавлейс. В программе на C есть два цикла while, один внутри другого. У программы Лавлейс не было циклов while, но она сгруппировала операции, и описала в примечании, почему они должны повторяться. Переменная v10 из оригинальной программы и в переводе на C, работает счётчиком, уменьшающимся с каждым проходом цикла – подобная конструкция знакома каждому программисту. В общем, кроме изобилия переменных с непонятными именами, программа на C не выглядит чем-то незнакомым.
Стоит также отметить, что перевод программы Лавлейс на C был не очень сложным, благодаря одной детали в её диаграмме. В отличие от таблиц Менабреа, в её таблице есть столбец «признак изменения значения переменной», благодаря которому гораздо проще отслеживать изменение состояния. Она добавляет каждой переменной надстрочный индекс, чтобы обозначить хранящиеся в них последовательные значения. Индекс 2, к примеру, означает, что используемое значение – это второе значение, присвоенное переменной с начала программы.
Первый программист?
После того, как я перевёл программу Лавлейс на язык C, я смог запустить её на компьютере. К моему разочарованию, результат получался неверный. После поиска ошибок я, наконец, понял, что проблема была не с моим кодом – баг содержался в изначальной программе!
В «диаграмме развития» Лавлейс пишет в четвёртой операции v5 / v4. Но правильно будет v4 / v5. Эта ошибка могла появиться при печати, а не у Лавлейс. Так или иначе, это самый старый компьютерный баг. Я удивился тому, что порядка десяти минут потратил на поиск самого первого бага в истории.
Джим Рэндал, другой блогер, переведший программу Лавлейс на Python, также отметил этот баг с делением и две других проблемы. О чём говорят нам небольшие ошибки в опубликованной программе Ады Лавлейс? Возможно, о том, что она пыталась написать не просто демонстрацию, а настоящую программу. Ведь нельзя же писать что-то, кроме игрушечных программ, избегая ошибок?
В одной из статей Википедии написано, что Лавлейс первая опубликовала «сложную программу». Возможно, именно так и стоит воспринимать её достижение. Менабреа в своей работе опубликовал «диаграммы развития» за год до публикации перевода Лавлейс. Бэббидж также написал более двадцати программ, так и не опубликованных. Поэтому не совсем верно писать, что Лавлейс написала или опубликовала первую программу, хотя всегда можно поспорить о том, что считать программой. И всё равно, программа Лавлейс намного опередила всё, что было опубликовано до неё. В самой длинной программе Менабреа было 11 операций и не было циклов и ветвлений. В программе Лавлейс было 25 операций и вложенный цикл (а, следовательно, и ветвление). Менабреа в конце своей работы написал следующее:
После постройки машины трудности сведутся к изготовлению карточек; но поскольку это всего лишь перевод алгебраических формул, посредством некоей простой записи будет довольно просто перепоручить их выполнение какому-нибудь рабочему.
Ни Бэббидж, ни Менабреа особенно не интересовались применением аналитической машины к задачам, выходящим за пределы математических проблем, которые и подвигли Бэббиджа к созданию вычислительных машин. Лавлейс поняла, что аналитическая машина была способна на гораздо большее, чем могли представить себе Бэббидж и Менабреа. Лавлейс также уловила, что «изготовление карточек» не станет механической работой, и что этим можно заниматься плохо или хорошо. Сложно оценить это, не понимая её программу из примечания G, и не видя, сколько заботы она проявила при её разработке. Но, проделав это, вы можете согласиться с тем, что Лавлейс, даже не будучи самым первым программистом, была первым программистом, заслужившим это название.
Автор: SLY_G






Класс