Алгоритм решения кроссвордов из регулярных выражений

Наверное, каждый, кто интересуется регулярными выражениями и читает Хабр, видел этот кроссворд из регулярных выражений:

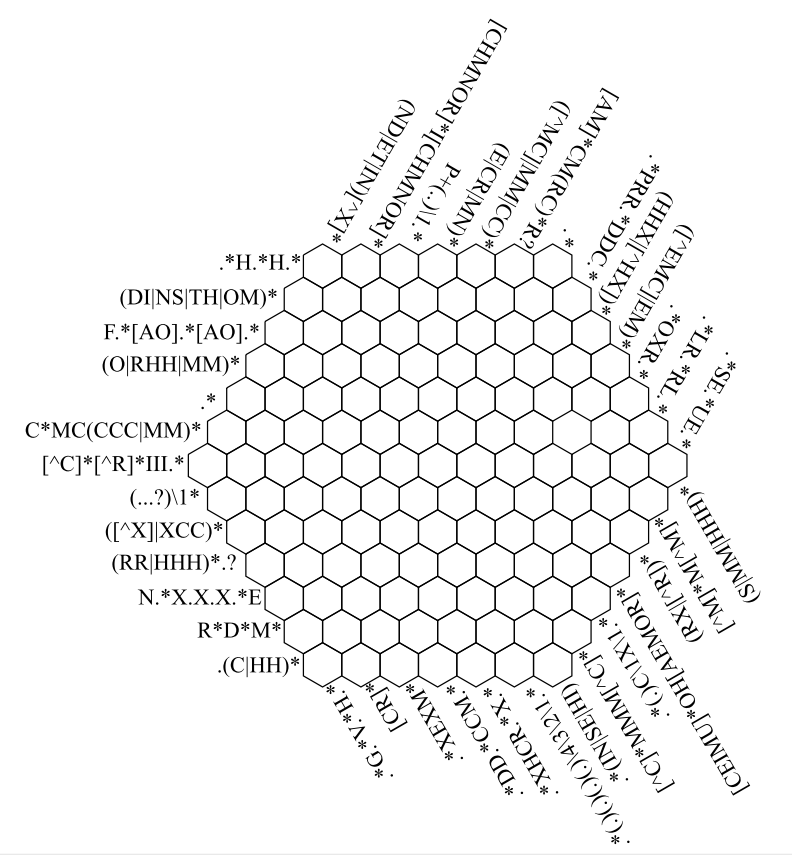
На его решение нужно от 30 минут до нескольких часов, а вот ваш компьютер способен решить его всего за несколько минут. Да и не только этот кроссворд, а любой кроссворд из регулярных выражений под силу алгоритму под катом.

Постараюсь приводить как можно меньше кода — весь код, написанный на Python3, вы найдете на ГитХабе.

Шаг 0. Условные обозначения и аксиомы

Аксиома. Если кроссворд из регулярных выражений имеет единственное конечное решение, то все символы, которые встретятся в решении заданы не отрицательными символьными классами и не метасимволом .

То есть пусть в неком кроссворде есть только символьные классы: [ABC], [^ABC], ., тогда решение кроссворда будет состоять исключительно из символов A, B и C.

Атом. "Атомом" будем называть символьный класс, одиночный литерал или метасимвол символьного класса, которые входят в состав разбираемого регулярного выражения.

Один "атом" — один символ в тексте. Понятие "атом" будет использовано, чтобы не путать их с символьными классами внутри регулярного выражения.

Например, регулярное выражение [ABC]*ABC[^ABC].w состоит из семи "атомов" [ABC], A, B, C, [^ABC], . , w

Карта кроссворда, карта. Массив с зависимостями между различными регулярными выражениями для одной ячейки поля кроссворда. Карта содержит сведения, что в данной ячейке поля находится (к примеру) 1-ый символ 3-го регулярного выражения, а также 5-ый символ 8-го регулярного выражения, а также 3-ий символ 12-го регулярного выражения. Проще говоря — в каких позициях регулярные выражения взаимопересекаются.

Шаг 1. Перебираем все варианты для "атомов"

Если попробовать решить кроссворд "в лоб" полным перебором всех символов, то сразу же возникнет проблема, что не получится ждать несколько миллионов лет- слишком много вариантов. И все же- алгоритм представляет собой полный перебор, но не отдельных символов, а "атомов".

Для примера, возьмем регулярное выражение .*(IN|SE|HI). В данном кроссворде оно должно представлять собой строку длиной 13 символов.

Сначала найдем в регулярном выражении все уникальные "атомы" регулярным выражением:

reChars = r"[^?[a-z]+]|[a-z]|."
reCharsC = re.compile( reChars, re.I )

Оно ищет символьные классы, одиночные символы и метасимвол "точка". На текущий момент нет поддержки метасимволов вроде w, d и т.п., только самое необходимое.

В рассматриваемом выражении мы найдем такие "атомы":

[ '.', 'I', 'N', 'S', 'E', 'H' ]

"Атомы" необходимо "атомизировать", чтобы рассматривать их строковую запись как неразрывное единое целое, а не отдельные символы:

def repl( m ):
    return "(?:"+re.escape( m.group(0) )+")"
self.regex2 = reCharsC.sub( repl, self.regex )

На входе .*(IN|SE|HI), на выходе (?:.)*((?:I)(?:N)|(?:S)(?:E)|(?:H)(?:I)). Что это даст? Теперь можно делать перебор всех "атомов" на длину 13 "атомов", к полученной строке применять self.regex2 и проверять на соответствие. Для примера:

Рег. выражение	"Атомное" рег.выражение	Длина	Строка	Результат
.*(IN|SE|HI)	(?:.)*((?:I)(?:N)|(?:S)(?:E)|(?:H)(?:I))	13	SE...........	не соответствует
-*-	-*-	-*-	..S.H.I......	не соответствует
-*-	-*-	-*-	...........IN	соответствует
-*-	-*-	-*-	...........SE	соответствует
-*-	-*-	-*-	...........HI	соответствует
[^X]*	(?:[^X])*	3	[^X][^X][^X]	соответствует

Результатом полного перебора к рассматриваемому регулярному выражению будет массив из трех элементов:

[ '...........IN', '...........SE', '...........HI' ]

Согласитесь, что весьма очевидный результат?

Поэкспериментировать с разными регулярными выражениями можно так:

import regexCrossTool as tool
print( tool.singleRegex( regex, length ).variants )

Шаг 2. Оптимизация

В предыдущем шаге было так просто сказано, что регулярное выражение .*(IN|SE|HI) даст всего 3 возможных варианта строки, но ведь на самом деле в выражении 6 "атомов" и длина 13 "атомов", что означает 6 в 13 степени вариантов для перебора.

Несколько дней перебора- не самая радужная перспектива, поэтому первая оптимизация по сути только для этого выражения, но на самом деле все оптимизации написаны честным образом — они разбирают регулярное выражение на входе и оптимизируют вычисления, если встретили подходящий шаблон.

Выражение .*(IN|SE|HI) оптимизировать весьма легко:

reCh = r"(?:"+reChars+")+"
re1 = r"(?!^)((?:"+reCh+r"|)+"+reCh+r")$"

Ищем альтернативу в конце строки, проверяем, что все части альтернативы имеют одну длину, выделяем все, что слева от этой альтернативы и обрабатываем отдельно с учётом того, что длина ожидаемого результата уменьшиться на длину части альтернативы.

singleRegex( ".*", 11 ) вернет всего один возможный вариант ...........
В цикле проходим по всем возвращенным вариантам и по всем частям альтернативы. Конкатенации возвращаем как результат для исходного регулярного выражения.

Время работы сократилось с нескольких дней до 20 минут. Хороший результат, но нужно лучше.

Следующая оптимизация очень похожа на первую. Оптимизируем регулярное выражение, которое представлено всего одной альтернативой и квантификатором к альтернативе. В данном кроссворде таких выражений несколько: (DI|NS|TH|OM)*, (O|RHH|MM)*, (E|CR|MN)*, (S|MM|HHH)*

Вместо полного перебора напишем несложную рекурсивную функцию:

def recur( arr, string, length ):
    res = []
    for i in arr:
        newstr = string + i
        lenChars = len( reCharsC.findall( newstr ) )
        if lenChars == length: res.append( newstr )
        elif lenChars > length: pass
        else:
            recres = recur( arr, newstr, length )
            for j in recres: res.append( j )
    return res

recur( r"(DI|NS|TH|OM)*", "", 12 )

Результат получим за доли секунды, а не за полторы минуты, как до оптимизации.

Ещё одна оптимизация применима к большинству регулярных выражений.
Ищем два и более одиночных литерала, не внутри символьного класса [...] и если до этих литералов не было скобки (.

Скобки избегаем, потому что она может означать что угодно: группу, условие, рекурсию. Парсить регулярные выражения регулярными выражениями не лучшая идея, поэтому лучше не заморачиваться сложными оптимизациями. Пусть оптимизируется что может, а что не может- подождём.

Забыл добавить, что все оптимизации проходят рекурсивно, поэтому к одному регулярному выражению может быть применено несколько оптимизаций. Рассмотрим выражение [AO]*abc[AO]*def — оно будет оптимизировано в 2 прохода.

Сначала заменим abc на [a], получим [AO]*[a][AO]*def, на втором проходе заменим def на [aa], получим [AO]*[a][AO]*[aa]

В результате вместо семи уникальных символьных классов [ '[AO]', 'a', 'b', 'c', 'd', 'e', 'f' ] стало три [ '[AO]', '[a]', '[aa]' ] — так полный перебор пойдет значительно быстрее, а перед тем как вернуть результат нужно произвести обратные замены [a] на abc и [aa] на def.

Итог оптимизаций: все варианты для всех регулярных выражений считаются примерно 40 секунд.

Шаг 3. Создаем карту кроссворда

Алгоритм находится в модуле hexaMap.py и рассматривать его смысла нет.
Передаешь ему длину минимальной грани гексагонального поля, а в ответ возвращается карта этого поля.

import hexaMap
maps = hexaMap.getMap( 7 )
printer = hexaMap.getPrinter( 7 )

printer — функция, которая получив результат вычислений распечатает решение в соответствии с картой.

Шаг 4. Объединение

Регулярное выражение .*(IN|SE|HI) вернет три варианта [ '...........IN', '...........SE', '...........HI' ], разместим их друг под другом, чтобы было понятнее о чем далее идет речь:

...........IN
...........SE
...........HI

В нулевой позиции может встретиться только метасимвол ., и так далее вплоть до 10-ой позиции.
В 11-ой позиции может быть три символа I, S, H
В 12-ой позиции может быть три символа N, E, I

Создадим сеты (set()) для каждой позиции отдельно — это и есть объединение.
Объединение происходит для каждого регулярного выражения отдельно и показывает в результате какие символы могут быть в определенных позициях в данном регулярном выражении.

Метасимволы и символьные классы тоже будут преобразованы в сеты. Помните аксиому? Создадим полный список символов из которых состоит решение кроссворда:

def getFullABC( self ):
    result = set()
    for i in self.cross.regexs:
        for j in reCharsC.findall( i ):
            if not re.match( r"[^", j ) and not j == ".":
                result = result.union( self.char2set( j ) )
    return result

self.fullABC = self.getFullABC()

Этот полный список соответствует метасимволу ., а отрицательные классы получаются путем вычитания из полного списка символов в отрицательном классе. Для конвертации "атомов" в сеты служит функция:

    def char2set( self, char ):
        char=char.lower()
        result = None
        def convDiap( diap ):
            return re.sub( r"([a-z])-([a-z])", repl, diap, flags=re.I )
        def repl( m ): # d-h -> defgh
            res = ""
            for i in range( ord( m.group(1) ), ord( m.group(2) )+1 ):
                res+= chr( i )
            return res
        char = char.replace( ".", "[a-z]" )
        char = convDiap( char )
        if re.fullmatch( "[a-z]", char, re.I ):
            result = set( [char] )
        elif re.fullmatch( r"[[a-z]+]", char, re.I ):
            result = set( char.replace( "[", "" ).replace( "]", "" ) )
        elif re.fullmatch( r"[^[a-z]+]", char, re.I ):
            result = set( char.replace( "[", "" ).replace( "]", "" ).replace( "^", "" ) )
            result = self.fullABC - result
        return result

Строчка char = char.lower() делает решение кроссворда регистронезависимым, если потребуется решать регистрозависимый кроссворд, то нужно будет убрать ее и все флаги re.I в коде, но это уже чистый хардкор, а не кроссворд.

Шаг 5. Пересечение

Результаты объединения просматриваем в соответствии с картой. К примеру, 1-ый символ 3-го регулярного выражения после объединения может содержать {'a', 'b', 'c', 'd'}
5-ый символ 8-го регулярного выражения после объединения может содержать {'a', 'c', 'd', 'x'}
3-ий символ 12-го регулярного выражения после объединения может содержать {'c', 'f', 's'}
Значит, в данной ячейке поля кроссворда может быть только символ c

Получив результат пересечения его нужно поместить обратно в результат объединения во все три измерения. Сеты {'a', 'b', 'c', 'd'}, {'a', 'c', 'd', 'x'}, {'c', 'f', 's'} заменяем на сет {'c'}.

Шаг 6. Фильтрация вариантов

В предыдущем шаге мы изменили результаты пересечения.
Например в 1-ый символ 3-го регулярного выражения вместо {'a', 'b', 'c', 'd'} вернули {'c'}, соответственно из вариантов нужно удалить те, которые давали в данную позицию {'a', 'b', 'd'}.

Если на этом шаге был удален хотя бы один вариант в любом регулярном выражении, то возвращаемся к шагу 4, то есть снова и снова объединяем, пересекаем и фильтруем, пока эти действия приносят плоды.

Вот что получим в результате:

      n h p e h a s         
     d i o m o m t h        
    f * * n x * x p h       
   m m * m m m * r h h      
  m c x n m m c r x e m     
 c m c c c c m m m m m m    
* r x r c m i i i h x l s   
 * * e * r * * * * o r e    
  v c x c c * h * x c c     
   r r r r h h h r r u      
    n c x d x * x l e       
     r r d d * * * *        
      g c c h h * *  

Звёздочки стоят там, где сеты продолжают содержать несколько значений, а значит — хвала создателям кроссворда, они создали его настолько грамотно, что без анализа обратных ссылок его невозможно решить.

Шаг 7. Анализ обратных ссылок

Обратные ссылки — единственное, что не было должным образом обработано в вариантах, потому что, например, регулярное выражение (...?)1* на длину 6 вернет единственный вариант ......, то, что в нем есть обратная ссылка никак не использовалось.

Анализ- громкое слово. В игру вновь вступает полный перебор. После полного перебора снова пробуем шаги 4-6 и так до получения результата:

      n h p e h a s         
     d i o m o m t h        
    f o x n x a x p h       
   m m o m m m m r h h      
  m c x n m m c r x e m     
 c m c c c c m m m m m m    
h r x r c m i i i h x l s   
 o r e o r e o r e o r e    
  v c x c c h h m x c c     
   r r r r h h h r r u      
    n c x d x e x l e       
     r r d d m m m m        
      g c c h h c c  

А что дальше?

Дальше можно решать кроссворды из любых регулярных выражений, какие бы замысловатые конструкции они не содержали, ведь алгоритм честно применяет это "атомизированное" регулярное выражение к "атомам", а значит в нем могут быть все возможные синтаксические конструкции любой сложности.

Если в кроссворде есть символьные классы, которые не поддерживаются на текущий момент- добро пожаловать на ГитХаб, ведь для добавления новых символьных классов нужно изменить лишь char2set и reChars.

Если хочется, чтобы в кроссворде могли быть символы вроде (, [, то опять же- ГитХаб открыт. Достаточно вместо парсинга регулярных выражений регулярными выражениями строить полноценное синтаксическое дерево регулярного выражения и анализировать его.

Спасибо за внимание, надеюсь, что Вы не заскучали от чтения этой небольшой статьи.

Автор: ReinRaus

Источник