В данной статье рассмотрены методы создания криптографических алгоритмов на основе SP-сетей. Приведены требования к криптографическим алгоритмам. Предложен метод для блочного шифрования данных на основе геометрического представления данных.
Алгоритмы шифрования и дешифрования данных широко применяются в компьютерной технике в системах сокрытия конфиденциальной и коммерческой информации от злонамеренного использования сторонними лицами.
На ранних стадиях развития криптографии методы шифрования данных были очень простые: сдвиги, перестановки, замены и т.д. На данной стадии развития вычислительной техники взлом этих методов занял бы несколько секунд.
В настоящее время построения криптостойких систем может быть осуществлено путём многократного применения простых криптографических преобразований (примитивов). В качестве таких примитивов Клод Шеннон предложил использовать подстановки (substitution) и перестановки (permutation). Схемы, реализующие эти преобразования, называются SP-сетями. Часто используемыми криптографическими примитивами являются также преобразования типа циклический сдвиг или гаммирование.
Важным требованием к криптоалгоритму является отсутствие линейности (то есть условия f(a) xor f(b) == f(a xor b)), в противном случае облегчается применение дифференциального криптоанализа к шифру.
Полная утрата всех статистических закономерностей исходного сообщения является важным требованием к симметричному шифру. Для этого шифр должен иметь «эффект лавины» — должно происходить сильное изменение шифроблока при 1-битном изменении входных данных (в идеале должны меняться значения половины бит шифроблока).
При разработке алгоритмов шифрования необходимо (в общем случае) сделать невозможным (в соотношении время/деньги) расшифровку методом полного перебора и любыми другими методами без знания ключа.
В данной работе рассматривается оригинальный метод шифрования, названный геометрическим, который позволяет нарушить нелинейность алгоритма.
Суть геометрического метода шифрования
Введем следующие обозначения:
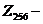символы алфавита (8-битное представление символов), мощность алфавита равна 256 символов (символы ASCII кодировки)
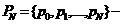исходный текст сообщения, где 
;
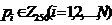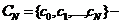зашифрованный текст, где 
;
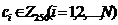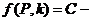процесс шифрования, где 
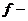алгоритм шифрования, а 
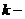ключ шифрования.
В качестве примера нарушения линейности алгоритма рассмотрим следующий пример.
Пускай имеется открытое сообщение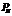 
=“Hello world”. Получим для этой строки коды символов:72 101 108 108 111 32 119 111 114 108 100.
Расположим эти коды на координатной сетке, приняв за Х-номер символа, за Y-код (значение) символа.
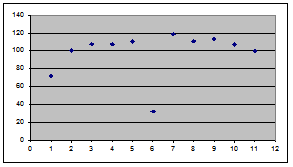
Рис. 1 Распределение исходного сообщения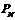 
на координатной сетке
Интерполированные данные представляют собой кривую на плоскости:
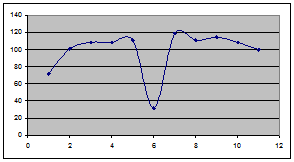
Рис. 2 Интерполированное сообщение на координатной сетке
Произведем перестановку элементов сообщения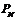 
так, что 
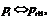где 
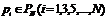. Получим новое сообщение 
.
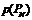Следующим действием добьемся увеличения «эффекта лавины». Для этого поменяем местами элементы, равноудаленные на m элементов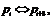 
— где 
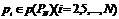. Получим новое сообщение 
.
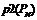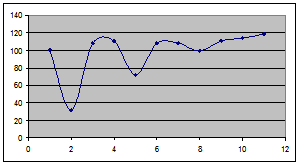
Рис. 3 Интерполированное сообщение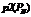 
на координатной сетке.
Интерполяцию набора точек произведем с помощью полинома Лагранжа
,
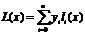где каждый элемент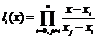 
.
Если проводить интерполяцию всего сообщения, то степень полинома Лагранжа будет возрастать факториально. Этот факт делает процесс интерполирования (для больших сообщений) очень трудоемким.
Именно поэтому будем исходное сообщение разбивать на группы. Размер группы может быть произвольным и зависит от ключа—от 3 до 5 символов в группе (для примера рассмотрим группу из 3 символов).
Для частного случая (группы из 3 элементов) полинома Лагранжа примет такой вид: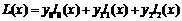 
(1)
Получим развернутый вид первого из трех слагаемых полинома:
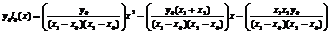(2)
Обозначим каждый коэффициент при неизвестных через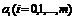 
, где m—количество элементов в группе (в нашем случае m=3).
В результате, получим следующий вид полинома Лагранжа:
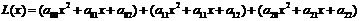(3)
Интерполировать блоки сообщения будем так, что последний элемент текущего блока будет первым элементом следующего. После интерполирования блоков сообщения получим набор кривых, изображенных на графике.
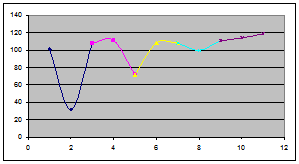
Рис 4. Интерполированное сообщение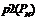 
блоками по 3 элемента
Предположим, что все коэффициенты полинома Лагранжа—это целые числа.
Представим полином в виде вектора.
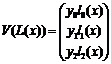(4)
Далее каждый элемент вектора разложим по формуле (2) и произведем замену коэффициентов при неизвестных через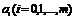 
, не учитывая самих неизвестных х, получим матрицу размерностью 3х3:
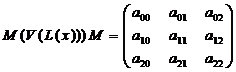(5)
Теперь собственно самая важная часть—необходимо произвести замену всех элементов матрицы по заранее определенному алгоритму.
Предлагается оригинальный вариант—выполнять перемешивание не символов блока, а всех битов из двоичного представления символов. Тогда количество вариантов станет достаточно большим для попыток взлома методом полного перебора—8 бит в каждом символе, 3 символа в строке—получаем 24 символа в строке, учтем 3 строки—получим 72 позиции. Соответственно вариантов будет порядка 72!=6*10103.
Представим элементы матрицы в бинарном виде:
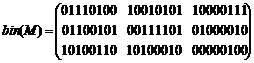(6)
Теперь в зависимости от ключа произведем циклические сдвиги по строкам и столбцам:
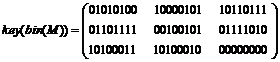(7)
Предположим, имеется такая часть ключа—…10 10100 00111 10….
Алгоритм перемешивания будет таким:
1. читаем два бита справа—10 (соответствует 2 в десятичной системе)— этим действием мы выбрали строку;
2. читаем следующие 5 бит справа—00111 (7 в десятичной системе)— этим мы выбрали количество разрядов для сдвига;
3. читаем следующие 5 бит справа—10100 (20 в десятичной системе)— этим мы выбрали столбец;
4. читаем следующие 2 бит справа—10 (2 в десятичной системе)— этим мы выбрали количество разрядов для сдвига.
Для сдвига одной строки и одного столбца необходимо по 7 бит информации (на каждый сдвиг). Предполагая, что будут сдвигаться все строки и столбцы (3 строки и 24 столбца) получим длину ключа 3*7+24*7=189. Округлим в большую сторону и получим максимальную длину ключа равную 192 бита.
Теперь на основе данной матрицы построим полином Лагранжа и получим новые значения для Yi: 164, 70, 248, 79, 126, 147, 105, 42, 216, 23, 152. И соответствующее им зашифрованное сообщение: « O і` цкУк ».
Расшифровка выполняется в обратном порядке. Если представить алгоритм шифрования в виде мнемосхемы:
.
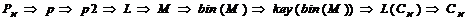Тогда алгоритм расшифровки будет выгладить следующим образом
.
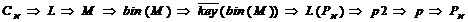Обозначения в мнемосхеме:
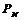—исходное сообщение;
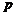—результат первого перемешивание элементов;
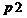—результат второго перемешивание элементов;
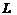—результат интерполирования сообщения;
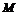—матрица, полученная из коэффициентов полинома Лагранжа;
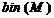—представление матрицы в двоичной форме;
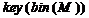— результат применения ключа;
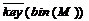— результат применения ключа в обратном порядке;
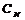—зашифрованное сообщение.
В статье предложен оригинальный метод шифрования данных, основанный на представлении данных в геометрическом виде. Метод имеет большую криптостойкость за счет нарушения линейности алгоритма и огромного числа возможных блоков данных.
Предложенный криптографический алгоритм может быть использован для защиты, как личных данных, так и некоторой секретной информации.
Прошу прощение за качество оформления. Жду комментариев и предложений.
Автор: karazhanov
