Введение
При формировании картографического изображения местности в поперечной равноугольной цилиндрической проекции Гаусса-Крюгера возникают проблемы, связанные с большими погрешностями и искажением формируемого изображения при удалении от осевого меридиана. Корнем этих проблем является то, что проекция Гаусса-Крюгера представляет собой шестьдесят “лепестков” шести-градусных зон, между которыми искусственно вносится расстояние 500 км. Это происходит из-за того, что стандартные методы визуализации не учитывают сужение зон к полюсам, а представляют их как прямоугольные. Для преодоления этих проблем существуют методы сшивания карт по одному осевому меридиану.
Метод «GKZone»
Одним из таких методов является метод динамического совмещения осевых меридианов, позволяющий компенсировать угол и расстояние между ними. Использование такого метода позволяет отобразить 2D карту в проекции Гаусса-Крюгера без видимых искажений, а также избежать избыточности исходных данных. Принцип данного метода состоит в том, что множество фрагментов листа карты, полученных при подготовке массивов данных, формируют, так называемые, зоны-лепестки.
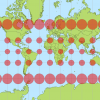
Для увеличения точности расположения объектов и уменьшения визуального искажение (ничтожно малое), можно задать нестандартный размер одной зоны равной, например, 1º или даже меньше. Размеры фрагментов, которыми заполняются зоны, задаются произвольно. Чем меньше размер фрагмент, тем выше качество визуализации.
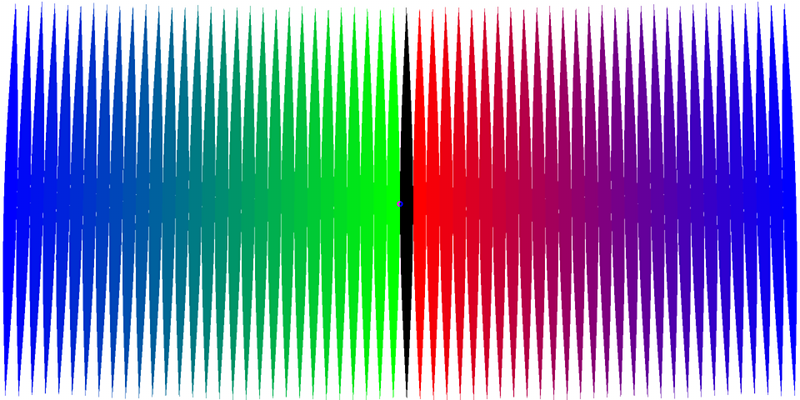
Рисунок 1. Пример разделения развернутой земной поверхности на зоны с шагом 6º
Метод совмещения заключается в следующем:
- Совершить пересчет координат точки интереса(относительно широты которой производиться склеивания) из геодезической/геоцентрической системы координат в проекцию Гауса-Крюгера.
- Определить координаты двух точек соприкосновения соседних осевых меридианов.
- Рассчитать угол поворота одной зоны относительно другой на текущей широте.
- Исходя из полученного угла сформировать матрицу преобразования для каждых соседних меридианов.
- Для позиционирования фрагмента необходимо умножить его координаты на соответствующую матрицу преобразования.
После выполнения перечисленных действий, мы получаем неразрывную сшитую карту. На рисунках 2 и 3 представлены изображения сшитых зон относительно различных северных широт.
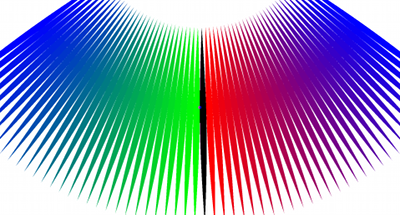
Рисунок 2. Сшито на 20° с.ш.
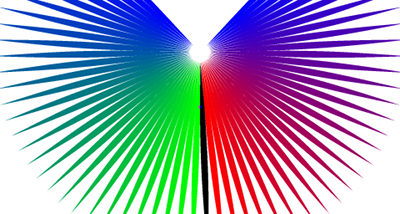
Рисунок 3. Сшито на 50° с.ш.
Причем координата широты у фрагментов склеиваемых зон остается неизменной, изменяется только координаты долготы. При слиянии зон таким способом, во время визуализации картографической информации местности, полностью отсутствует зрительная деформация и минимизируется погрешность. На рисунке 4 показано, что окружность будет изображена без видимых искажений, если карта будет сшита описываемым образом.

Рисунок 4. Изображение окружности
Заключение
Большое значение в визуализации картографической информации имеет качество изображения, но минимизация погрешностей отображения и возможность расчета приблизительного расстояния по полученному изображению также играет большую роль. Описанный метод удовлетворяет оба параметра и успешно используется при разработке картографических систем.
К сожалению данный метод применим только для карт масштабов до 1:1000000, так как при увеличении масштаба становятся явно видны участки совмещения.
Список литературы
- Курс высшей геодезии, П, С. Закатов, Москва «НЕДРА» 1976
- ГОСТ Р51794-2008
От автора
Данная статья является выдержкой из статьи для будущей конференции. Детали и расчеты я решил пока не выкладывать, так как они еще редактируются. Название метода — GKZone, конечно не самое удачное, но это рабочее название метода в исходном коде. Поэтому приветствуются предложения по более понятному названию метода.
Надеюсь данная статья будет полезна для людей, интересующихся картографией, потому что проекция Меркатора широко освещена в различных источниках, а проекция Гаусса-Крюгера нет.
Жду конструктивной критики статьи и предложений по ее улучшению.
Автор: xorbot