
Когда вы входите в мой дом… эм… Мы с женой хотели, чтобы у нас были какие-либо произведения искусства в доме, которые были бы личными и также связанными с тем, чем мы занимаемся. И поэтому вы можете увидеть две вещи: одна из них это кривая дракона, я расскажу вам о ней больше через минуту. И другая это вот эта работа. Это строчка из “Дороги к мудрости” Пита Хайна:
 Должны мы,
Должны мы,
Чтоб к мудрости
Вечной добраться,
Что нам
Так заманчиво
Брезжит,
Опять
И опять,
И опять
Ошибаться,
Но реже
И реже,
И реже.
Это одна из моих любимых фраз. Своего рода история всей моей жизни — это совершение ошибок и попытки научиться чему-то на них. Эту фразу спроектировали в форме суперэллипса, который является одним из великих открытий Пита Хайна. Этот эллипс более полный и он использовался во многих архитектурных изделиях.
И так, какова идея кривой дракона? Это то, что появилось на свет благодаря паре физиков в поздних шестидесятых.

Возьмите кусок бумаги и согните его, снова согните, и снова и вы делаете это n раз. N равно девяти в случае с кривой дракона на стене слева.

Когда вы смотрите на это, вы видите, что некоторые сгибы загнуты вверх, а некоторые внутрь. Если вы представите, что движетесь по этой кривой, то вы поворачиваете налево здесь, затем поворачиваете налево здесь, опять поворачиваете налево здесь, но затем вы поворачиваете направо и затем другой поворот направо, и опять поворот налево и так далее.

Это узор, состоящий из лево и право. Самое потрясающее, что если вы продолжите эту кривую, проделаете это 9 раз, а затем откроете все эти сгибы под углом девяносто градусов, то вы получите дорожку, которая начинает заполнять пространство и создает прекрасный практический узор. Начнем здесь, от этой плитки, например.

Если вы немного приблизите камеру, то увидите, что мы с женой написали здесь наши имена, но мы можем поговорить об этой истории позже. Эта кривая начинается, поворачивает налево, снова налево, затем направо, затем налево, затем снова налево и так далее. Это именно тот узор, который вы получите, складывая бумагу. Так как я сложил лист 9 раз, на стене показано 512 шагов. Ну, вероятно, 511. Кривая заканчивается вот здесь и она все продолжается, но в середине она становится очень запутанной.
Замечательная вещь, с точки зрения гиковского искусства, заключается в том, что вам нужно только три вида плитки.

Вам нужна абсолютно пустая плитка или плитка, на которой только одна петля, как здесь, или плитка, на которой две петли, как эта. И, разумеется, я могу взять плитку с двумя петлями и перевернуть ее, допустим, в эту сторону. Тогда она не будет соединяться здесь, но она образует вот здесь изолированный круг.

Я должен был посчитать сколько мне понадобится пустых плиток, сколько понадобится плиток с одной петлей и прочее. Мы сделали макет из оберточной бумаги и картона и хранили его в квартире, в которой мы жили, пока наш дом проектировали. И мы решили, что это классный дизайн и было бы круто иметь подобное в нашем доме, когда его наконец построили.

Нам обоим нравилась плитка от HIT Ceramics в Саусалито, Калифорнии и у нас был макет дизайна, поэтому мы пошли, чтобы посмотреть на керамику и поговорить с людьми работающими там. И нам было интересно смогут ли они сделать под заказ для нас определенное количеством пустых плиток, плиток с одной петлей и т.д. Они ответили, что да, они могут это сделать, но они делают плитки квадратиком 3.5 дюйма.
А для моего дизайна требовались 2 дюймовый квадратики. Вычисления никак нельзя было изменить, даже если бы я сменил 9 на 8. Это был бы такой же интересный узор, но в то же время он был бы огромным и не выглядел бы нормально в таком масштабе.
Такого вида узор очень привлекателен именно в таком размере, а не в большем размере. Мы видимо выглядели очень расстроенными и разочарованными, потому что человек, с которым мы разговаривали, увидел, что мы расстроены, так как мы проехали весь этот путь с этой прекрасной идеей. И он сказал: “Погодите, в июне мы уходим в отпуск, закрываем нашу фабрику, но у нас тут есть охранник.
Вы можете прийти и использовать наше оборудование, мы позволим вам использовать нашу глину и изготовить плитки. Если вы собираетесь обрезать их по размеру 2х2 дюйма, то я позволю вам надеть наши очки и мы потом обожжем плитку для вас. Так мы и сделали. Мы пошли туда и провели там целый день, делая всю эту плитку, в том числе несколько запасных плиток. И мы разместили наши инициалы на этой плитке, на начальной точке. Затем был произведен обжиг этой плитки. Некоторые отметины от огня все еще можно иногда увидеть, плитка кое-где немного треснула во время обжига.

У нас их все же было 9. После восьми шагов линия находится здесь, после 16 здесь, на 32 шаге я здесь.
Шли годы, я наконец разместил главу в своей книге “Веселье и игры”, в которой говорится об этом. И я прочитал все статьи по этой теме, я написал о кривой дракона и пришел к шокирующему открытию, что это *показывает на стену* неверно.

Вы получаете эту кривую за счет 9 сгибов, но 9 сгиб я сделал не в том направлении. Вместо того чтобы пойти в эту сторону, я пошел в другую.
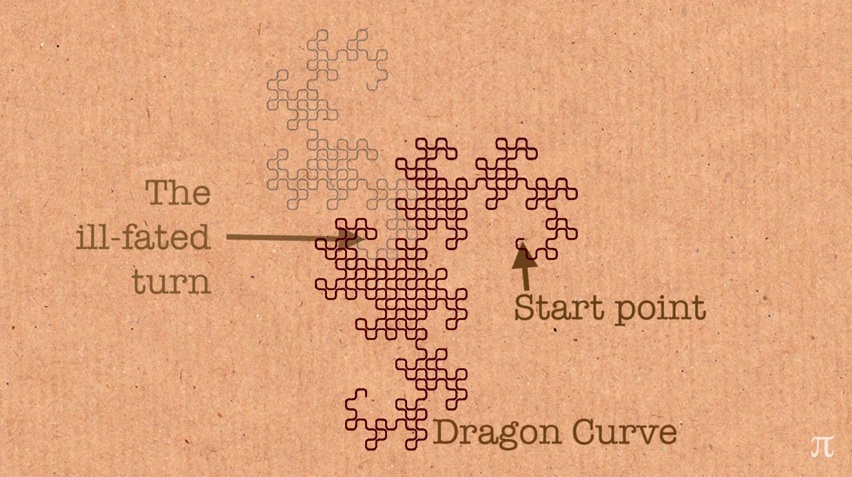
Последняя половина этой кривой на самом деле имеет другой сгиб. С точки зрения математики я жил с этой кривой 30 лет и не осознавал, что у меня математическая ошибка в дизайне.
— Что вы чувствуете по этому поводу?
— Я прочувствовал смысл фразы:
Чтоб к мудрости
Вечной добраться,
Что нам
Так заманчиво
Брезжит,
Опять
И опять,
И опять
Ошибаться,
Но реже
И реже,
И реже.
О школе GoTo
- 17-30 июня, 15-28 июля, 12-25 августа
Летние проектные GoTo школы в Подмосковье. - Группа в ВК
- Подписаться на рассылку
Автор: MagisterLudi







