
Нормальное распределение (распределение Гаусса) всегда играло центральную роль в теории вероятностей, так как возникает очень часто как результат воздействия множества факторов, вклад любого одного из которых ничтожен. Центральная предельная теорема (ЦПТ), находит применение фактически во всех прикладных науках, делая аппарат статистики универсальным. Однако, весьма часты случаи, когда ее применение невозможно, а исследователи пытаются всячески организовать подгонку результатов под гауссиану. Вот про альтернативный подход в случае влияния на распределение множества факторов я сейчас и расскажу.
Краткая история ЦПТ. Еще при живом Ньютоне Абрахам де Муавр доказал теорему о сходимости центрированного и нормированного числа наблюдений события в серии независимых испытаний к нормальному распределению. Весь 19 и начало 20 веков эта теорема послужила ученым образцом для обобщений. Лаплас доказал случай равномерного распределения, Пуассон – локальную теорему для случая с разными вероятностями. Пуанкаре, Лежандр и Гаусс разработали богатую теорию ошибок наблюдений и метод наименьших квадратов, опираясь на сходимость ошибок к нормальному распределению. Чебышев доказал еще более сильную теорему для суммы случайных величин, походу разработав метод моментов. Ляпунов в 1900 году, опираясь на Чебышева и Маркова, доказал ЦПТ в нынешнем виде, но только при существовании моментов третьего порядка. И только в 1934 году Феллер поставил точку, показав, что существование моментов второго порядка, является и необходимым и достаточным условием.
ЦПТ можно сформулировать так: если случайные величины независимы, одинаково распределены и имеют конечную дисперсию отличную от нуля, то суммы (центрированные и нормированные) этих величин сходятся к нормальному закону. Именно в таком виде эту теорему и преподают в вузах и ее так часто используют наблюдатели и исследователи, которые не профессиональны в математике. Что в ней не так? В самом деле, теорема отлично применяется в областях, над которыми работали Гаусс, Пуанкаре, Чебышев и прочие гении 19 века, а именно: теория ошибок наблюдений, статистическая физика, МНК, демографические исследования и может что-то еще. Но ученые, которым не достает оригинальности для открытий, занимаются обобщениями и хотят применить эту теорему ко всему, или просто притащить за уши нормальное распределение, где его просто быть не может. Хотите примеры, они есть у меня.
Коэффициент интеллекта IQ. Изначально подразумевает, что интеллект людей распределен нормально. Проводят тест, который заранее составлен таким образом, при котором не учитываются незаурядные способности, а учитываются по-отдельности с одинаковыми долевыми факторами: логическое , мысленное проектирование, вычислительные способности, абстрактное
Второй пример: изменения финансовых показателей. Исследования изменения курса акций, котировок валют, товарных опционов требует применения аппарата математической статистики, а особенно тут важно не ошибиться с видом распределения. Показательный пример: в 1997 году нобелевская премия по экономике была выплачена за предложение модели Блэка — Шоулза, основанной на предположении нормальности распределения прироста фондовых показателей (так называемый белый шум). При этом авторы явно заявили, что данная модель нуждается в уточнении, но всё, на что решилось большинство дальнейших исследователей – просто добавить к нормальному распределению распределение Пуассона. Здесь, очевидно, будут неточности при исследовании длинных временных рядов, так как распределение Пуассона слишком хорошо удовлетворяет ЦПТ, и уже при 20 слагаемых неотличимо от нормального распределения. Гляньте на картинку снизу (а она из очень серьезного экономического журнала), на ней видно, что, несмотря на достаточно большое количество наблюдений и очевидные перекосы, делается предположение о нормальности распределения.
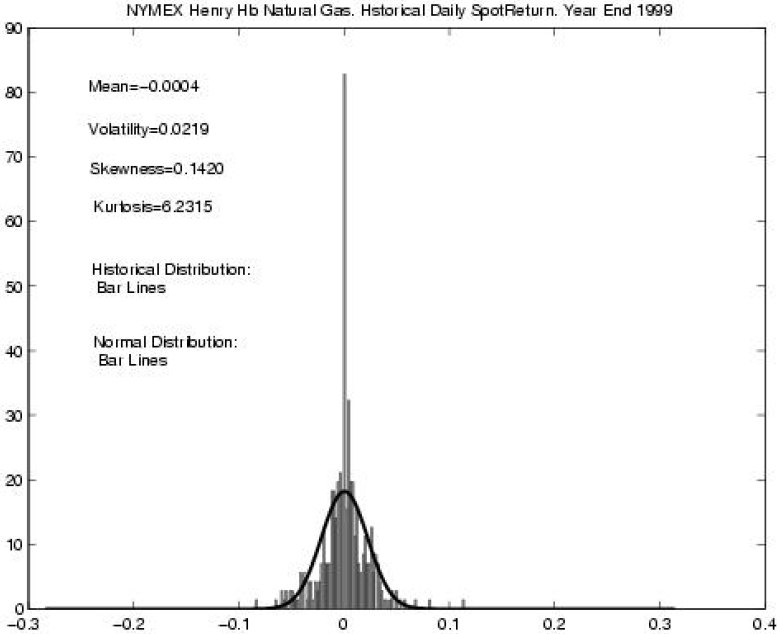
Весьма очевидно, что нормальными не будет распределения заработной платы среди населения города, размеров файлов на диске, населения городов и стран.
Общее у распределений из этих примеров – наличие так называемого «тяжелого хвоста», то есть значений, далеко лежащих от среднего, и заметной асимметрии, как правило, правой. Рассмотрим, какими еще, кроме нормального могли бы быть такие распределения. Начнем с упоминаемого ранее Пуассона: у него есть хвост, но мы же хотим, чтобы закон повторялся для совокупности групп, в каждой из которых он наблюдается (считать размер файлов по предприятию, зарплату по нескольким городам) или масштабировался (произвольно увеличивать или уменьшать интервал модели Блэка — Шоулза), как показывают наблюдения, хвосты и асимметрия не исчезают, а вот распределение Пуассона, по ЦПТ, должно стать нормальным. По этим же соображениям не подойдут распределения Эрланга, бета, логонормальное, и все другие, имеющие дисперсию. Осталось только отсечь распределение Парето, а вот оно не подходит в связи с совпадением моды с минимальным значением, что почти не встречается при анализе выборочных данных.
Распределения, обладающее необходимыми свойствами, существуют и носят название устойчивых распределений. Их история также весьма интересна, а основная теорема была доказана через год после работы Феллера, в 1935 году, совместными усилиями французского математика Поля Леви и советского математика А.Я. Хинчина. ЦПТ была обобщена, из нее было убрано условие существования дисперсии. В отличие от нормального, ни плотность ни функция распределения у устойчивых случайных величин не выражаются (за редким исключением, о котором ниже), все что о них известно, это характеристическая функция (обратное преобразование Фурье плотности распределения, но для понимания сути это можно и не знать).
Итак, теорема: если случайные величины независимы, одинаково распределены, то суммы этих величин сходятся к устойчивому закону.
Теперь определение. Случайная величина X будет устойчивой тогда и только тогда, когда логарифм ее характеристической функции 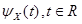 представим в виде:
представим в виде:
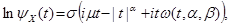
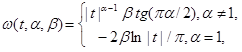
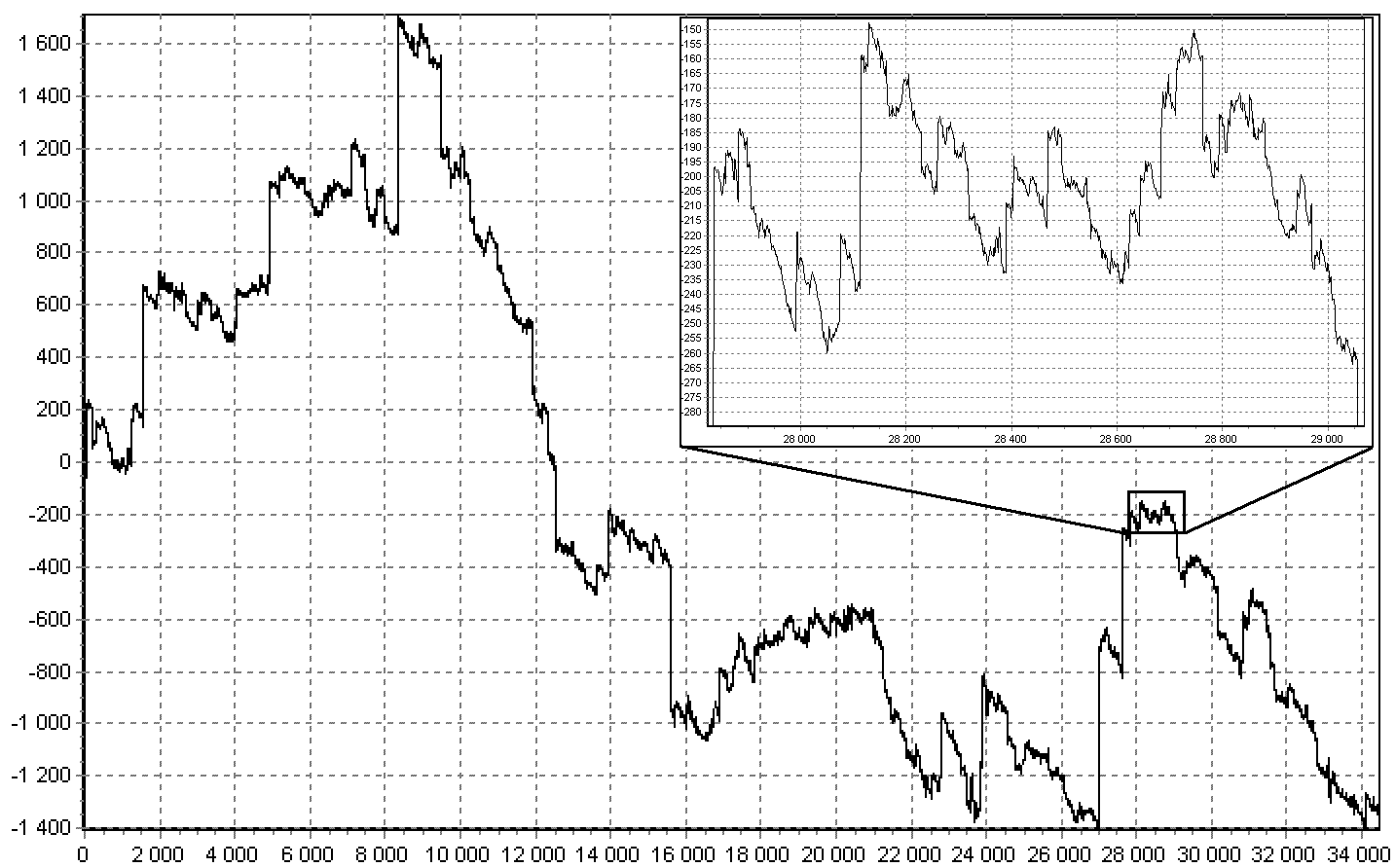
где 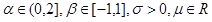 .
.
В самом деле, ничего сильно сложного здесь нет, просто надо объяснить смысл четырех параметров. Параметры сигма и мю – обычные масштаб и смещение, как и в нормальном распределении, мю будет равно математическому ожиданию, если оно есть, а оно есть, когда альфа больше одного. Параметр бета – асимметрия, при его равенстве нулю, распределение симметрично. А вот альфа это характеристический параметр, обозначает какого порядка моменты у величины существуют, чем он ближе к двум, тем больше распределение похоже на нормальное, при равенстве двум распределение становиться нормальным, и только в этом случае у него существуют моменты больших порядков, также в случае нормального распределения, асимметрия вырождается. В случае, когда альфа равна единице, а бета нулю, получается распределение Коши, а в случае, когда альфа равна половине, а бета единице – распределение Леви, в других случаях не существует представления в квадратурах для плотности распределения таких величин.
В 20 веке была разработана богатая теория устойчивых величин и процессов (получивших название процессов Леви), показана их связь с дробными интегралами, введены различные способы параметризации и моделирования, несколькими способами были оценены параметры и показана состоятельность и устойчивость оценок. Посмотрите на картинку, на ней смоделированная траектория процесса Леви с увеличенным в 15 раз фрагментом.
Именно занимаясь такими процессами и их приложением в финансах, Бенуа Мандельброт придумал фракталы. Однако не везде было так хорошо. Вторая половина 20 века прошла под повальным трендом прикладных и кибернетических наук, а это означало кризис чистой математики, все хотели производить, но не хотели думать, гуманитарии со своей публицистикой оккупировали математические сферы. Пример: книга «Пятьдесят занимательных вероятностных задач с решениями» американца Мостеллера, задача №11:

Авторское решение этой задачи, это просто поражение здравого смысла:

Такая же ситуация и с 25 задачей, где даются ТРИ противоречащих ответа.
Но вернемся к устойчивым распределениям. В оставшейся части статьи я попытаюсь показать, что не должно возникать дополнительных сложностей при работе с ними. А именно, существуют численные и статистические методы, позволяющие оценивать параметры, вычислять функцию распределения и моделировать оные, то есть работать так же, как и с любым другим распределением.
Моделирование устойчивых случайных величин. Так как все познается в сравнении, то напомню сначала наиболее удобный, с точки зрения вычислений, метод генерирования нормальной величины (метод Бокса – Мюллера): если 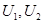 – базовые случайные величины (равномерно распределены на [0, 1) и независимы), то по соотношению
– базовые случайные величины (равномерно распределены на [0, 1) и независимы), то по соотношению 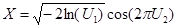 получится стандартная нормальная величина.
получится стандартная нормальная величина.
Теперь зададим заранее альфу и бету, пусть V и W, независимые случайные величины: V равномерно распределена на 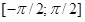 , W экспоненциально распределена с параметром 1, определим
, W экспоненциально распределена с параметром 1, определим 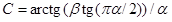 и
и 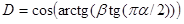 , тогда по соотношению:
, тогда по соотношению:
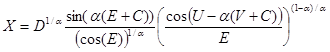
получим устойчивую случайную величину, для которой мю равна нулю, а сигма единице. Это так называемая стандартная устойчивая величина, которую для общего случая (при альфа не равном единице), просто достаточно помножить на масштаб и прибавить смещение. Да, соотношение сложнее, но оно все равно достаточно простое, чтобы его использовать даже в электронных таблицах (Ссылка). На рисунках снизу показаны траектории моделирования модели Блэка — Шоулза сперва для нормального, а затем для устойчивого процесса.
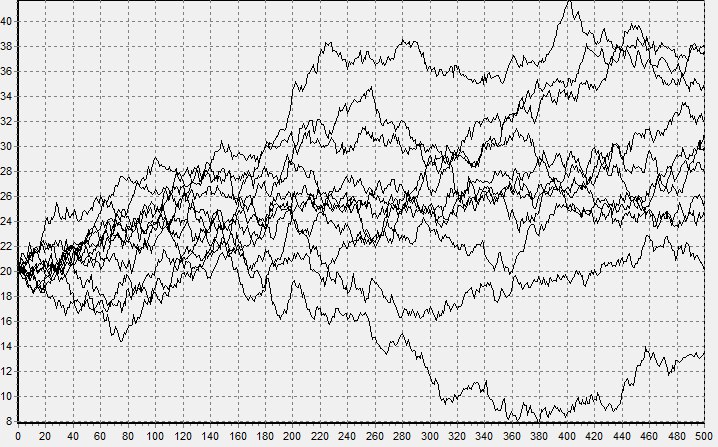
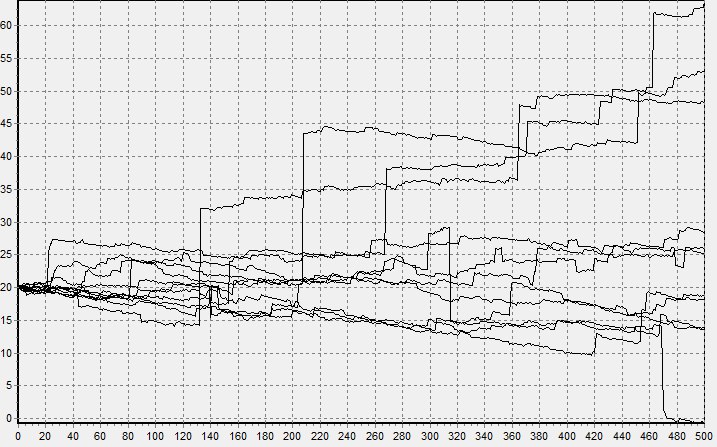
Можете поверить, график изменения цен на биржах больше похож на второй.
Оценка параметров устойчивого распределения. Так как вставлять формулы на хабре достаточно сложно, я просто оставлю ссылку на статью, где подробно разбираются всевозможные методы для оценки параметров, или на мою статью на русском языке, где приводятся только два метода. Также можно найти замечательную книгу, в которой собрана вся теория по устойчивым случайным величинам и их приложениям (Zolotarev V., Uchaikin V. Stable Distributions and their Applications. VSP. M.: 1999.), или ее чисто научный русский вариант (Золотарев В.М. Устойчивые одномерные распределения. – М.: Наука, Главная редакция физико-математической литературы, 1983. – 304 с.). В этих книгах также присутствуют методы для вычисления плотности и функции распределения.
В качестве заключения могу лишь порекомендовать, при анализе статистических данных, когда наблюдается асимметрия или значения, сильно превосходящие ожидаемые, спрашивать самих себя: «правильно ли выбран закон распределения?» и «а все ли с нормальным распределением нормально?».
Автор: paunch






