Рекурсия: см. рекурсия.
Все программисты делятся на 112 категорий: кто не понимает рекурсию, кто уже понял, и кто научился ею пользоваться. В общем, гурилка из меня исключительно картонный, так что постигать Дао Рекурсии тебе, читатель, всё равно придётся самостоятельно, я лишь постараюсь выдать несколько волшебных пенделей в нужном направлении.
Прикладное программирование всегда занимается решением прикладных задач путем прикладывания усилий программиста для достижения результата в неидеальных условиях. Именно исходя из неидеальности этого мира и ограниченности ресурсов и складывается потребность в программистах: кому-то ведь надо помогать теоретикам упихать их стройную и красивую теорию в практику.
— Как она сложена?
— Превосходно! Только рука немного торчит из чемодана.
Именно пытаясь разместить стройную теорию алгоритма в жесткий рюкзак реальных ресурсов и приходится постоянно кроить по живому, перепаковывать, и вместо красивых и стройных определений Фибоначчи:
def fib(n):
if n<0: raise Exception("fib(n) defined for n>=0")
if n>1: return fib(n-1) + fib(n-2)
return n
приходится городить всевозможные грязные хаки, начиная от:
@memoized
def fib(n):
if n<0: raise Exception("fib(n) defined for n>=0")
if n>1: return fib(n-1) + fib(n-2)
return n
И заканчивая вообще:
def fib(n):
if n<0: raise Exception("fib(n) defined for n>=0")
n0 = 0
n1 = 1
for k in range(n):
n0, n1 = n1, n0+n1
return n0
Так что же такое рекурсия?
Рекурсия, по сути, это доказательство по индукции. Мы рассказываем, как получить результат для некоего состояния, предполагая что у нас есть результат для другого набора состояний, так же рассказываем, как получить результат в тех состояниях, к которым всё скатывается так или иначе.
Если вы ждете гостей и вдруг заметили на своем костюме пятно, не огорчайтесь. Это поправимо.
Например, пятна от растительного масла легко выводятся бензином. Пятна от бензина легко снимаются раствором щелочи.
Пятна от щелочи исчезают от уксусной эссенции. Следы от уксусной эссенции надо потереть подсолнечным маслом.
Ну, а как выводить пятна от подсолнечного масла, вы уже знаете...
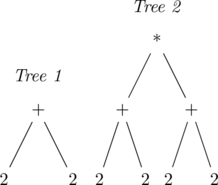Теперь давайте рассмотрим классический пример: обход дерева в глубину. Впрочем нет, давайте рассмотрим другой пример: нам надо распечатать дерево выражений в форме обратной польской записи. То есть для дерева 1 мы хотим напечатать «2 2 +» а для дерева 2 «2 2 + 2 2 + *».
begin{tikzpicture}
node (is-root) {+}
child { node {2} }
child { node {2} };
path (is-root) +(0,+0.5tikzleveldistance)
node {textit{Tree 1}};
end{tikzpicture}
begin{tikzpicture}
node (is-root) {*}
child { node {+} [sibling distance=1cm] child {node{2}} child {node{2}} }
child { node {+} [sibling distance=1cm] child {node{2}} child {node{2}} };
path (is-root) +(0,+0.5tikzleveldistance)
node {textit{Tree 2}};
end{tikzpicture}
Как легко видеть, задача превращается в простой «обход дерева в глубину»: для каждого узла выводим содержимое всех его дочерних элементов, после чего выводим сам узел. То есть код будет:
class TreeNode(object):
def __init__(self, value=None, children=[]):
self.value = value
self.children = children
def printTree(node):
for child in node.children:
printTree(child)
print node.value,
def main():
tree1 = TreeNode("+", [ TreeNode(2), TreeNode(2) ])
tree2 = TreeNode("*", [ TreeNode("+", [ TreeNode(2), TreeNode(2) ]), TreeNode("+", [ TreeNode(2), TreeNode(2) ]) ])
print "Tree1:",
printTree(tree1)
print
print "Tree2:",
printTree(tree2)
print
if __name__ == "__main__":
main()
Казалось бы, всё отлично! Код прекрасно работает до тех пор, пока дерево соответствует требованиям: любой узел имеет массив детей (возможно пустой) и какое-либо значение. Кто скажет какое еще требование к этому дереву?
Не буду томить. Требование: не сильно большая глубина дерева. Как так? А вот как:
def buildTree(depth):
root = TreeNode("1")
node = root
for k in range(depth):
node = TreeNode("--", [ node ])
return node
def depthTest(depth):
tree = buildTree(depth)
print "Tree of depth", depth, ":",
printTree(tree)
def main():
for d in range(10000):
depthTest(d)
Запускаем, и ууупс! «Tree of depth 997: RuntimeError: maximum recursion depth exceeded». Лезем в документацию, и обнаруживаем функцию sys.getrecursionlimit. А теперь давайте отойдём от мира интерпретируемых языков, и перейдём в мир языков, которые запускаются прямо на процессоре. Например, на C++.
Мысленно перепишем 1-в-1 этот код на С++ (оставлю эту задачу читателю в качестве разминки), и попробуем найти предел, когда приложение упрется в ограничение…
#include <string>
#include <vector>
#include <iostream>
using namespace std;
class TreeNode {
public:
string value_;
vector<TreeNode*> children_;
TreeNode(const string& value, const vector<TreeNode*>& children):
value_(value), children_(children) {}
virtual ~TreeNode() {}
};
void printTree(const TreeNode* node) {
for(auto i : node->children_)
printTree(i);
cout << node->value_ << " ";
}
TreeNode* buildTree(const int depth) {
auto root = new TreeNode("1", {});
auto node = root;
for(int i = 0; i<depth; i++) {
vector<TreeNode*> children;
children.push_back(node);
node = new TreeNode("--", children);
}
return node;
}
void depthTest(const int depth) {
auto tree = buildTree(depth);
cout << "Tree of depth " << depth << ": ";
printTree(tree);
cout << endl;
}
int main() {
for(int d=60000;; d+=16384) {
depthTest(d);
}
}
Запускаем… «Bus error (core dumped)». Судя по gdb, в момент падения стек глубиной 104790 фреймов. А что произойдёт, если мы захотим печатать не просто подряд через пробелы, а выводить еще "{" и "}" вокруг выражений? Ну то есть для дерева 1 чтобы результатом было {2 2 +} а для дерева 2 — {{2 2 +}{2 2 +}*}? Перепишем…
def printTree(node):
opened = False
for child in node.children:
if not opened:
print "{",
opened = True
printTree(child)
print node.value,
if opened:
print "}",
Ничего не изменилось, по прежнему падает при попытке распечатать дерево глубиной 997. А теперь то же самое, но на плюсах… Опа. Глубина стека при падении — 87327. Стоп. Мы всего-то добавили одну локальную переменную, никак не влияющую на алгоритм и суть происходящего, а предельный размер дерева сократился на 17%! А теперь самое весёлое — всё это сильно зависит от опций компилятора, от того, на какой платформе выполняется, в какой ОС и с какими настройками.
Но не это самое смешное. Давайте представим, что эту функцию использует другая функция. Всё хорошо, если она одна такая — мы можем подсчитать, на сколько же фактических шагов меньше максимальная глубина. А если эта функция используется из другой рекурсивной? Тогда возможности этой функции будут зависеть от глубины другой функции.
Вот таким образом наш прекрасный простой алгоритм перестаёт внезапно влезать в наш несовершенный чемодан. Предоставлю читателю самому представить как хорошо иметь подобные ограничения в сервисе, который запущен в продакшене и предоставляет некий сервис ничего не подозревающим хакерам, которые только и делают, что тычут в этот сервис своими грязными fuzzy тестерами.
Так в чем же проблема?
Использование рекурсивного алгоритма подразумевает использование практически не контролируемого ресурса: стека вызовов.
Во-1х, мы не можем точно знать сколько уже его использовано. Во-2х, мы не можем точно знать, сколько его еще осталось. В-3их мы не можем гарантировать доступность определённого размера этого ресурса к каждому вызову. В 4-ых, мы не можем фиксировать расход данного ресурса. Таким образом, мы попадаем в зависимость от ресурса, контролировать и распределять который чертовски сложно. В результате, мы не можем гарантировать каких либо характеристик данной функции/сервиса. Хорошо, если наш сервис работает в managed контексте: java, python, .net итп. Плохо, если сервис работает в неконтролируемой среде: javascript (с которым вообще всё плохо). Еще хуже, если сервис работает на C++, и глубина рекурсии зависит от данных, переданных пользователем.
Что же делать?
Если мы работаем не на микроконтроллере, о объёме стека можно не задумываться: для обычной цепочки вызовов его должно хватать. При условии, разумеется, что мы заботимся гигиене локальных переменных: большие объекты и массивы выделяются используя память (new/malloc). Однако использование рекурсии подразумевает, что вместо ограниченного количества вызовов, у нас их будет просто счетное.
Итак, чтобы избавиться от проблем, созданных рекурсией, можно сделать следующее (от простого к сложному):
— Жестко ограничить максимальный размер/формат/числа во входящих данных. Привет, zip бомбам и иже с ними — порой даже маленький входящий пакет может устроить большой переполох.
— Жестко ограничить максимальную глубину вызовов некоторым числом. Важно помнить, что это число должно быть ОЧЕНЬ небольшим. То есть порядка сотен. И обязательно добавить тесты, которые проверяют, что программа с этим максимальным числом не ломается. Причем с максимальным числом на всех возможных ветках исполнения (привет выделению локальных переменных по требованию). И не забывать проверять этот тест на разных опциях компилияции и после каждого билда.
— Жестко ограничить объём используемый стека. Используя сложные обходные маневры и знания о практической реализации исполнения в железе можно получить размер стека, который использован сейчас (типа взятия адреса локальной volatile переменной). В некоторых случаях (например, через libunwind в linux'е) можно получить так же доступный объём стека текущему потоку, и взять между ними разницу. При использовании подобного метода важно иметь тесты, проверяющие, что отсечение работает гарантированно и при всех вариантах входных данных — например, может получиться весело, если проверка идёт в одном методе, который рекурсивен через 3-4 других. И оно может упасть в промежуточном… Но только в режиме релиза, после inline'а некоторых функций, например. Впрочем, тут еще важны тесты на максимальную допустимую сложность, чтобы невзначай не отсечь часть корректных входных запросов, которыми клиенты реально пользуются.
— Лучший способ: избавиться от рекурсии.
И не лги, что ты волен и свят — Ты пленен и неволен.
Я раскрыл пред тобой небосвод!
Времена изменяют свой ход — Посмотри на ладони…Беспредельная сладость свободы
Отринуть свободу
© Сергей Калугин
Да-да. После постижения Дао рекурсии постигаешь так же Дао отказа от рекурсии. Практически все рекурсивные алгоритмы имеют нерекурсивные аналоги. Начиная от более эффективных (см. выше Фибоначчи), и заканчивая эквивалентными, использующими очередь в памяти вместо стека вызовов.
Каноническая нерекурсивная реализацию обхода дерева в глубину:
def printTree(node):
stack = [ (node, False, False) ]
while len(stack)>0:
i = len(stack)-1
node, visited, opened = stack[i]
if not visited:
for child in reversed(node.children):
if not opened:
print "{",
opened = True
stack.append( (child, False, False) )
visited = True
stack[i] = (node, visited, opened)
else:
print node.value,
if opened:
print "}",
del stack[i]
Как легко видеть, алгоритм не изменился, но вместо использования стека вызовов используется массив stack, размещенный в памяти, и хранящий как контекст обработки (в нашем случае — флаг opened) так и контекст обработки (в нашем случае — до или после обработки детей). В случаях, когда нужно что-то делать между каждым из рекурсивных вызовов, либо добавляются фазы обработки. Обратите внимание: это уже оптимизированный алгоритм, складывающий всех детей в стек сразу, и именно поэтому складывающий в обратном порядке. Это гарантирует сохранение того же порядка, что и у исходного нерекурсивного алгоритма.
Вот этот же код, только написанный «в лоб», сохраняя контекст (заодно, выводящий запятые между элементами):
def printTree(node):
stack = [ (node, 0) ]
while len(stack)>0:
i = len(stack)-1
node, phase = stack[i]
if phase < len(node.children):
child = node.children[phase]
if phase == 0:
print "{",
if phase > 0:
print ",",
stack.append( (child, 0) )
stack[i] = (node, phase+1)
else:
print node.value,
if phase>0:
print "}",
del stack[i]
Да, переход на безрекурсивные технологии не совсем бесплатен: мы платим периодически более дорогим — динамическим выделением памяти для организации стека. Впрочем, это окупается: в «ручной стек» сохраняются не вообще все локальные переменные, а только минимально необходимый контекст, размер которого уже можно контролировать. Вторая статья расходов: читабельность кода. Код, записанный в нерекурсивном виде несколько сложнее для восприятия за счет ветвлений от текущего состояния. Решение этой проблемы лежит уже в области организации кода: вынесение шагов в отдельные функции и грамотное их наименование.
Злоключение
Несмотря на наличие некоего «налога на обезрекурсивание», я лично считаю его обязательным к уплате в любом месте, где идёт обработка данных, так или иначе поступивших от пользователя.
А как не используете рекурсию вы?
Автор: datacompboy
