Предложен оригинальный новый алгоритм блочного шифрования, предназначенный для реализации на широко распространенных микроконтроллерах общего назначения. Алгоритм «NASH» основан на принципах современной «легковесной криптографии», но использует управляемые сдвиги, что позволяет при сохранении уровня стойкости ограничиваться меньшим числом раундов, повышая скорость обработки данных. Алгоритм «NASH» может быть использован для защиты обмена данными между устройствами в так называемых сетях «интернета вещей», а также для защиты данных, записываемых на компактные персональные носители (флэш-память, карты MicroSD и т. д.).
Ключевые слова: шифрование, блочный алгоритм шифрования, легковесная криптография, раундовая функция, управляемые сдвиги, развертка ключа.
В связи с широким распространением в промышленных системах, системах управления и массовых бытовых устройствах потребительского рынка микроконтроллеров общего назначения они стали относительно дешевы и широко доступны. В то же время их возможности изменились настолько, что стало возможно говорить о реализации сложных криптографических преобразований [1, 2]. Однако реализация на микроконтроллерах стандартов шифрования не может обеспечить приемлемой скорости шифрования. Поэтому для достижения высокой скорости было предложено несколько специальных алгоритмов шифрования, получивших название «легковесных» [3, 4, 5]. Наиболее эффективными среди них следует признать алгоритмы SPECK и SIMON, разработанные АНБ [6, 7]. В них выражена идея алгоритма шифрования, состоящего из большого количестве простых преобразований, которая высказывалась в письмах 50-х годов в АНБ лауреатом нобелевской премии по экономике Джоном Нэшэм [9].
Мы поставили своей целью разработать легковесный алгоритм блочного шифрования, который не уступал бы по стойкости упомянутым алгоритмам АНБ, но позволял бы несколько сократить количество раундов, что делает его еще более быстрым. В честь Джона Нэша (John Nash) мы назвали алгоритм NASH.
Схема алгоритма
Схема алгоритма NASH выглядит следующим образом. Текст разбивается на полублоки по 2**n бит, блок шифруется r раундов на последовательности раундовых ключей k(i), получаемых из главного ключа по алгоритму «расширения ключа». Блок данных разбивается на левый и правый полублоки (L(i), R(i)) по 2**n бит каждый, с которыми на (i+1)-м раунде производятся следующие преобразования
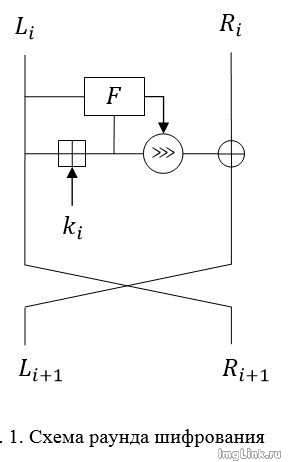
Уравнения шифрования блока данных на (i+1)-м раунде выглядят так:
R(i+1)=L(i)
L(i+1)=((L(i)⊞k(i))⋙F(L(i),L(i)⊞k(i)))⊕R(i)
В последнем раунде шифрования блока не меняются местами полублоки L(i+1), R(i+1).
Детали раундового преобразования
Размер полублока равен 2**n, где n=5 или 6, соответственно размер полублока равен 32 или 64 бита. Соответственно предлагается размер блока 64 или 128 бит.
Смешивание с раундовым ключом k(i): ⊞ – функция сложение двух целых чисел по модулю 2^n.
Управляемый циклический сдвиг:
- для размера блока 64 бита (полублока – 32 бита) — циклический сдвиг вправо на одно из 4 значений (11, 14, 10, 19).
- для размера блока 128 бит (размер полублока – 64 бита) — циклический сдвиг вправо на одно из 4 значений (37, 34, 38, 29).
Функция управления сдвигами
Интерпретируем полублок L(i) как вектор значений булевой функции от n переменных, и первый выходной бит F получаем как значение данной функции на наборе битов из L(i)⊞k(i) вида 2**i-1, где i=1, …, n, то есть как значение L(i) ((L(i)⊞k(i))[2**1-1,…,2**n-1]), нумерация битов полублока от 0 до 2**n-1.
Интерпретируем L(i)⊞k(i) как вектор значений булевой функции от n переменных, и второй выходной бит F получаем как значение данной функции на наборе битов из L(i) вида 2**i-1, где i=1,…, n, то есть как (L(i)⊞k(i))(L(i) [2**1-1,…,2**n-1]), нумерация битов полублока от 0 до 2^n-1.
Для размера блока 64 бита (соответственно, полублока – 32 бита):
00 соответствует циклическому сдвигу на 11;
01 соответствует циклическому сдвигу на 14;
10 соответствует циклическому сдвигу на 10;
11 соответствует циклическому сдвигу на 19.
Число раундов r:
для размера блока 64 (полублока — 32): r=24;
для размера блока 128 (полублока — 64): r=28.
Размер ключа: 128, 192 или 256 бит.
Функция выработки раундовых ключей
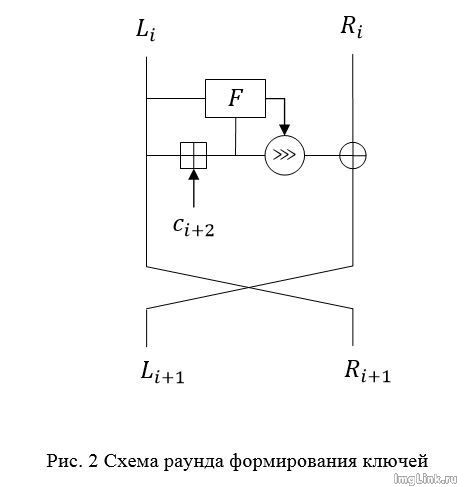
L(0)=с(0), R(0)=с(1), где значение константы с(i) получается следующим образом.
Ключ разбивается на L блоков длины 2^n, еще 8-L блоков получаем как значения квадратного корня из первых простых чисел (√2, √3, √5 и т. д., оставляем только мантиссу – дробную часть без порядка. C99 / C11 80-бит long double берем биты из последних 64 бит).
Данные блоки соответствуют с(0), с(1), …, с(7).
Далее при вычислении с(i) берем константу с(i) с индексом (i mod 6)+2 и складываем его по модулю 2 с номером раунда с(i)=i⨁с((i mod 6)+2).
В качестве раундового ключа берем k(i)=L(i+1).
2. Interenet of Things. 2016 URL: http:// www.gemalto.com / iot
3. McKay K., Bassham L., Turan M., Mouha N., DRAFT NISTIR 8114 Report on Lightweight Cryptography Computer Security Division Information Technology Laboratory NIST, 2016 URL: www.nist.gov
4. D. Dinu, Y. Le Corre, D. Khovratovich, L. Perrin, J. Großschädl, A. Biryukov, Triathlon of Lightweight Block Ciphers for the Internet of Things, Report on Lightweight Cryptography Lightweight Cryptography Workshop 2015, Computer Security Division Information Technology Laboratory NIST, 2015 URL: www.nist.gov
5. N. Mouha, B. Mennink, A. Van Herrewege, D. Watanabe, B. Preneel, I. Verbauwhede, Chaskey: a Lightweight MAC Algorithm for Microcontrollers, Lightweight Cryptography Workshop 2015, Cryptography Computer Security Division Information Technology Laboratory NIST, 2015 URL: www.nist.gov
6. H. Tschofenig, M. Pegourie-Gonnard, Performance of State-of-the-Art Cryptography on ARM-based Microprocessors, NIST Lightweight Cryptography Workshop 2015
7. R. Beaulieu, D. Shors, J. Smith, S. Treatman-Clark, B. Weeks, L. Wingers, Simon and Speck: Block Ciphers for the Internet of Things, National Security, Agency 9800 Savage Road, Fort Meade, MD, 20755, USA, Memo 9 July 2015
8. C. Shannon, Communication theory of secret systems, Bell Systems Techn. J. (1949) 656-715
9. J. Nash, Letter to NSA, 1955, URL: www.nsa.gov/public_info/press_room/2012/nash_exhibit_shtm
Автор: lancrypto