За 10 лет существования ivi мы собрали базу из 90000 видео разной длины, размера и качества. Каждую неделю появляются сотни новых. У нас есть гигабайты метаданных, которые полезны для рекомендаций, упрощают навигацию по сервису и настройку рекламы. Но извлекать информацию непосредственно из видео мы начали только два года назад.
В этой статье я расскажу, как мы разбираем фильмы на структурные элементы и зачем нам это нужно. В конце есть ссылка на репозиторий Github с кодом алгоритмов и примерами.
Из чего состоит видео?
Видео-ролик имеет иерархическую структуру. Речь о цифровом видео, поэтому на самом нижнем уровне — пиксели, цветные точки, из которых состоит неподвижная картинка.
Неподвижные картинки называются кадрами — они сменяют друг друга и создают эффект движения.

На монтаже кадры нарезают на группы, которые по задумке режиссёра меняют местами и склеивают обратно. Последовательность кадров от одной монтажной склейки до другой в английском языке называют термином shot. К сожалению, русская терминология неудачная, потому что в ней такие группы тоже называются кадрами. Чтобы не запутаться, давайте использовать английский термин. Только введём русскоязычный вариант: «шот».
Шоты объединяют в группы по смыслу, они называются сценами. Сцена характеризуется единством места, времени и персонажей.
Мы можем легко получить отдельные кадры и даже пиксели этих кадров, потому что так устроены алгоритмы кодирования цифрового видео. Эта информация необходима для воспроизведения.
Границы шотов и сцен получить гораздо сложнее. Могут помочь исходники из программ для монтажа, но нам они не доступны.
К счастью, это умеют делать алгоритмы, пусть и не идеально точно. Об алгоритме деления на сцены я сейчас и расскажу.
Зачем нам это надо?
Мы решаем задачу поиска внутри видео и хотим автоматически протегировать каждую сцену каждого фильма на ivi. Разделение на сцены — важная часть этого пайплайна.
Знать, где начинаются и кончаются сцены, нужно и для создания синтетических трейлеров. У нас уже есть алгоритм, который их генерирует, но пока что детекция сцен там не используется.
Рекомендательной системе тоже полезно разбиение на сцены. Из них получают признаки, которые описывают, какие фильмы нравятся пользователям по структуре.
Какие есть подходы к решению задачи?
Задачу решают с двух сторон:
- Берут целое видео и ищут границы сцен.
- Сначала делят видео на шоты, а потом объединяют их в сцены.
Мы пошли вторым путём, потому что его проще формализовать, и есть научные статьи на эту тему. Мы уже умеем делить видео на шоты. Осталось эти шоты собрать в сцены.
Первое, что хочется попробовать — это кластеризация. Взять шоты, превратить в векторы, а потом классическими алгоритмами кластеризации векторы разбить на группы.
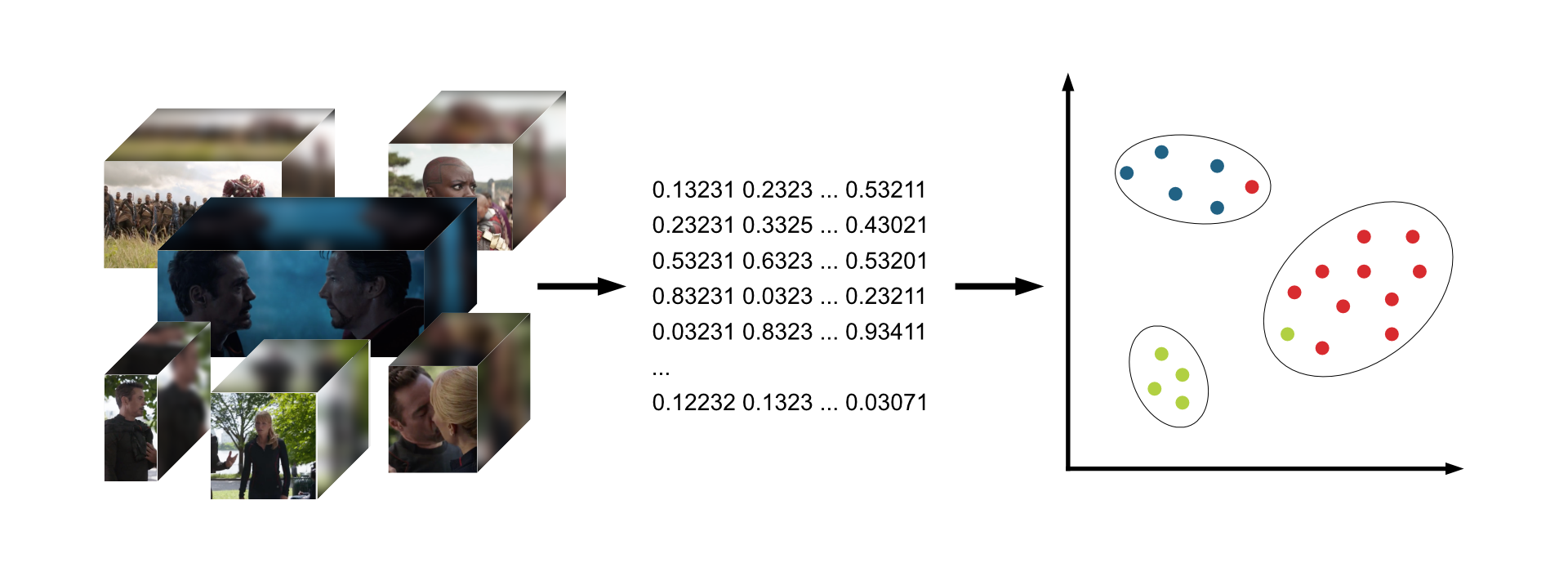
Главный недостаток такого подхода: он не учитывает, что шоты и сцены следуют друг за другом. Между двумя шотами одной сцены не может стоять шот из другой сцены, а при кластеризации такое возможно.
В 2016 году Дэниел Ротман и его коллеги из IBM предложили алгоритм, который учитывает временную структуру, и сформулировали объединение шотов в сцены как задачу Optimal Sequential Grouping:
- дана последовательность из
шотов
- нужно так разделить её на
отрезков так, чтобы это разделение было оптимально.
Что такое оптимальное разделение?
Пока будем считать, что 
Очевидно, что нужна какая-то метрика. Метрик придумали аж три, в их основе лежит идея попарных расстояний между шотами.
Подготовительные этапы такие:
- Превращаем шоты в векторы (гистограмму или выходы предпоследнего слоя нейронной сети)
- Находим попарные расстояния между векторами (евклидово, косинусное или какое-то другое)
- Получаем квадратную матрицу
, где каждый элемент — это расстояние между шотами
и
.

Эта матрица симметрична, а на главной диагонали у неё всегда будут нули, потому что расстояние вектора до самого себя равно нулю.
Вдоль диагонали прослеживаются тёмные квадраты — области, где соседние шоты похожи друг на друга, соответственно меньше расстояние.
Если мы выбрали хорошие эмбеддинги, которые отражают семантику шотов, и выбрали хорошую функцию расстояния, то эти квадраты — и есть сцены. Найдём границы квадратов — найдём и границы сцен.
Глядя на матрицу, израильские коллеги сформулировали три критерия оптимального разбиения:

Какой из критериев оптимального разбиения выбрать?
Хорошая лосс-функция для задачи Optimal Sequential Grouping имеет два свойства:
- Если фильм состоит из одной сцены, то где бы мы ни пытались разделить его на две части, значение функции всегда будет одинаковым.
- При правильном разбиении на сцены значение будет меньше, чем при неправильном.
Оказывается, 


В первом эксперименте сделаем синтетическую матрицу попарных расстояний, заполнив её равномерным шумом. Если попытаемся разделить на две сцены, получим следующую картинку:
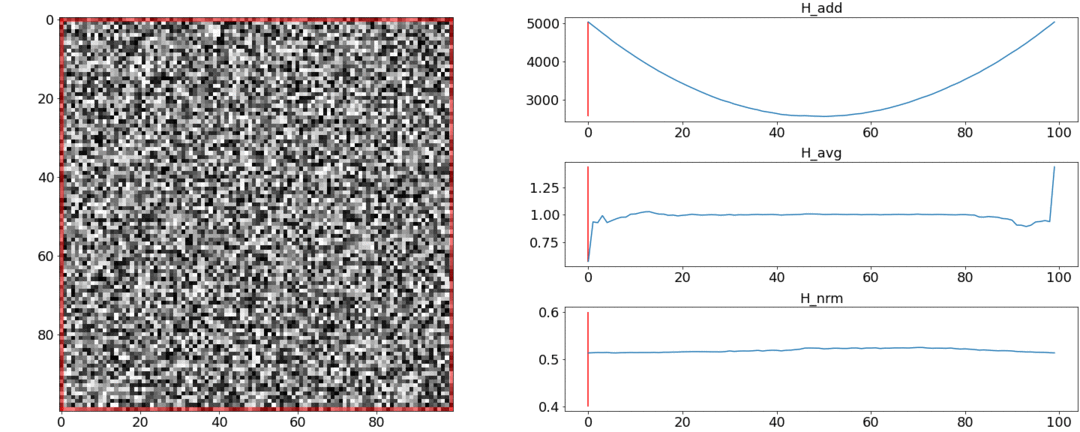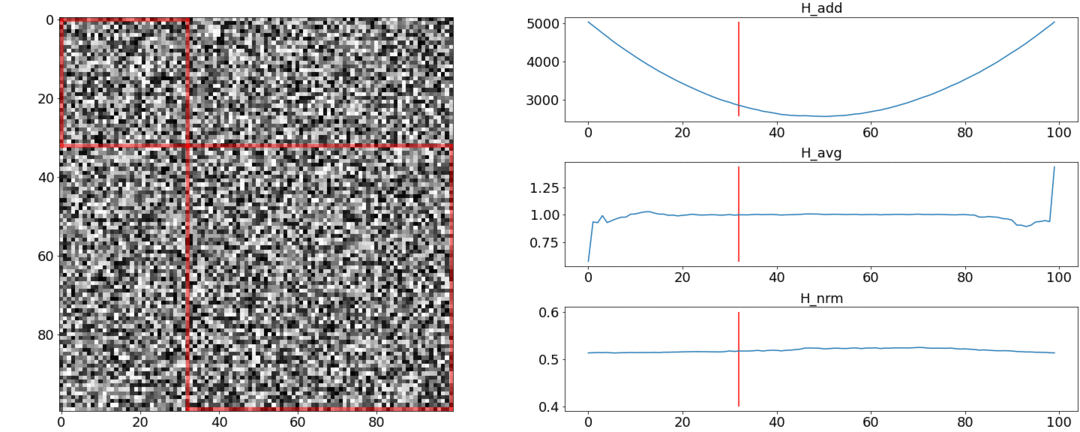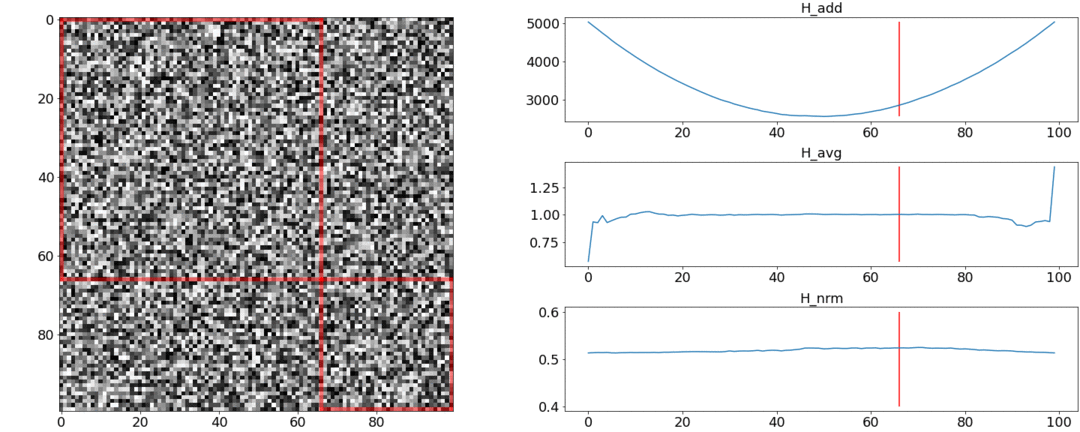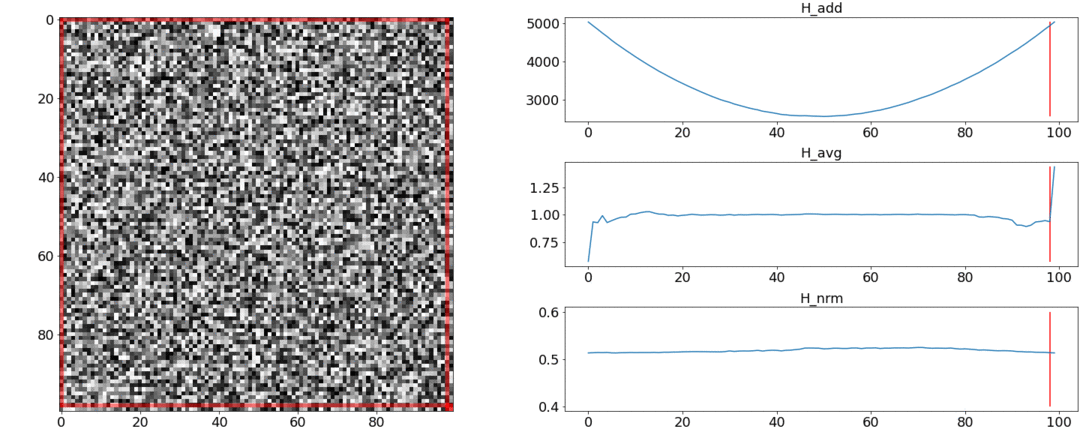



Во втором эксперименте сделаем такую же матрицу с равномерным шумом, но вычтем из неё два квадрата, как если бы у нас было две сцены, слабо отличающиеся друг от друга.
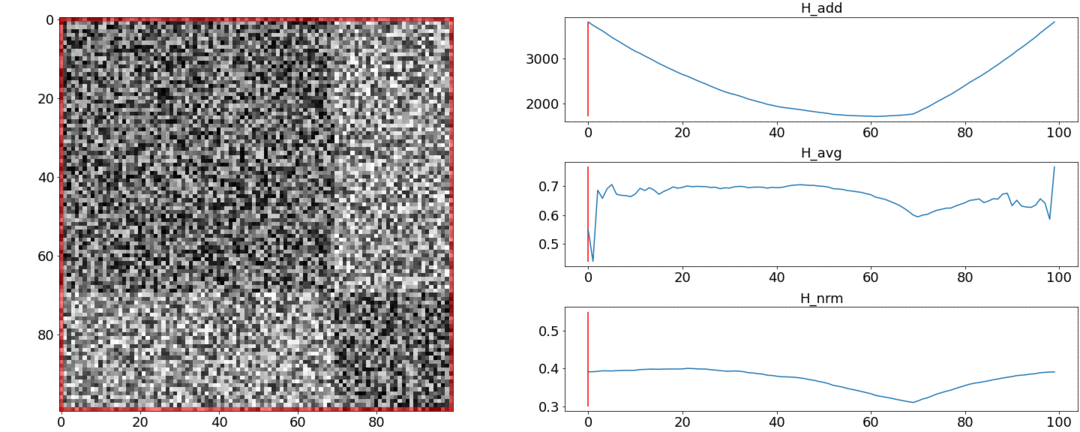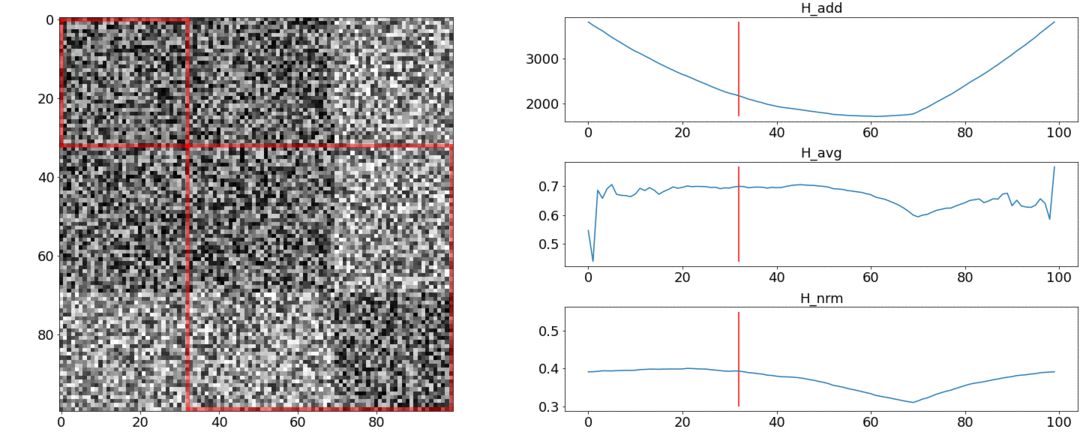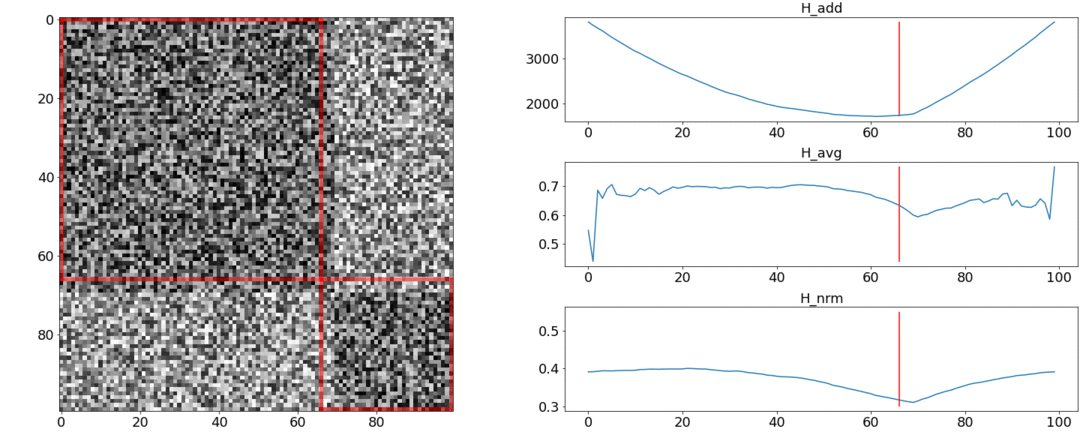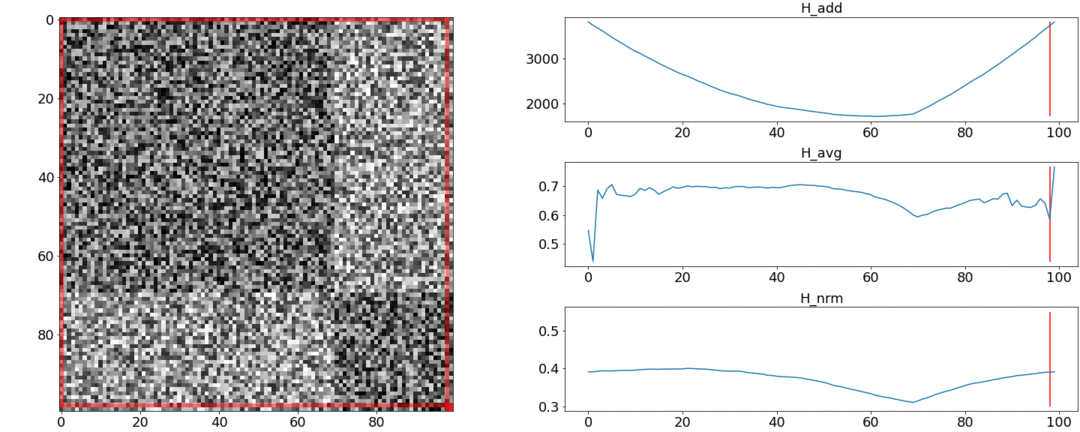
Чтобы обнаружить эту склейку, функция должна принимать минимальное значение при 




Тесты тоже показывают, что самое точное разбиение достигается при использовании 
Дэниел Ротман и его группа предложили искать оптимальное разбиение методом динамического программирования. Задачу разбивают на подзадачи в рекурсивной манере и решают по очереди. Этот метод даёт глобальный оптимум, но чтобы его найти, нужно перебрать для каждого ![Как мы научились делить видео на сцены с помощью хитрой математики - 29 $[2..K]$](https://www.pvsm.ru/images/2020/04/16/kak-my-nauchilis-delit-video-na-sceny-s-pomoshyu-hitroi-matematiki-29.svg)


Без твиков и ускорений оптимизация 



Нам удалось внести некоторое улучшение и ускорить оптимизацию с помощью техники Memorization — кеширования результатов рекурсии в памяти, чтобы не считать одно и то же по многу раз. Но, как покажут тесты ниже, сильного прироста в скорости добиться не удалось.
Как оценивать количество сцен?
Группа из IBM предположила, что раз многие строки матрицы линейно зависимы, то количество квадратных кластеров вдоль диагонали будет примерно равно рангу матрицы.
Чтобы его получить и при этом отфильтровать шумы, нужно сингулярное разложение матрицы 
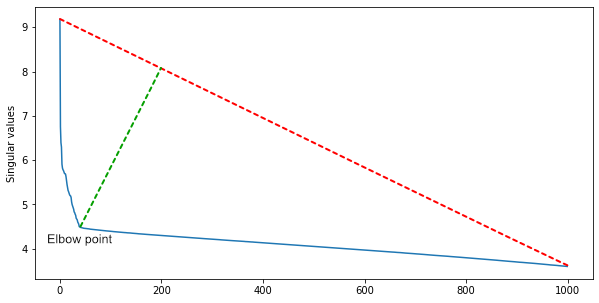
Среди сингулярных значений, отсортированных по убыванию, находим локтевую точку — ту, с которой уменьшение значений резко замедляется. Индекс локтевой точки — это примерное количество сцен в фильме.
Для первого приближения этого достаточно, но можно дополнить алгоритм эвристиками для разных жанров кино. В экшн-фильмах сцен больше, а в артхаусе — меньше.
Тесты
Мы хотели понять две вещи:
- Настолько ли разница в скорости драматична?
- Насколько страдает точность при использовании более быстрого алгоритма?
Тесты разделили на две группы: синтетические и на реальных данных. На синтетических тестах сравнили качество и скорость работы обоих алгоритмов, а на реальных — померяли качество самого быстрого алгоритма. Тесты на скорость выполняли на MacBook Pro 2017, 2.3 GHz Intel Core i5, 16 GB 2133 MHz LPDDR3.
Синтетические тесты качества
Мы сгенерировали 999 матриц попарных расстояний размером от 12 до 122 шотов, случайным образом разделили их на 2-10 сцен и добавили сверху нормальный шум.
Для каждой матрицы нашли оптимальные разбиения с точки зрения 

Precision и Recall для интервала мы считаем вот по таким формулам:
F1 считаем как обычно, подставляя интервальные Precision и Recall:
Чтобы сопоставить предсказанные и истинные отрезки в рамках фильма, для каждого предсказанного находим истинный отрезок с наибольшим пересечением и считаем метрику для этой пары.
Вот какие результаты получились:
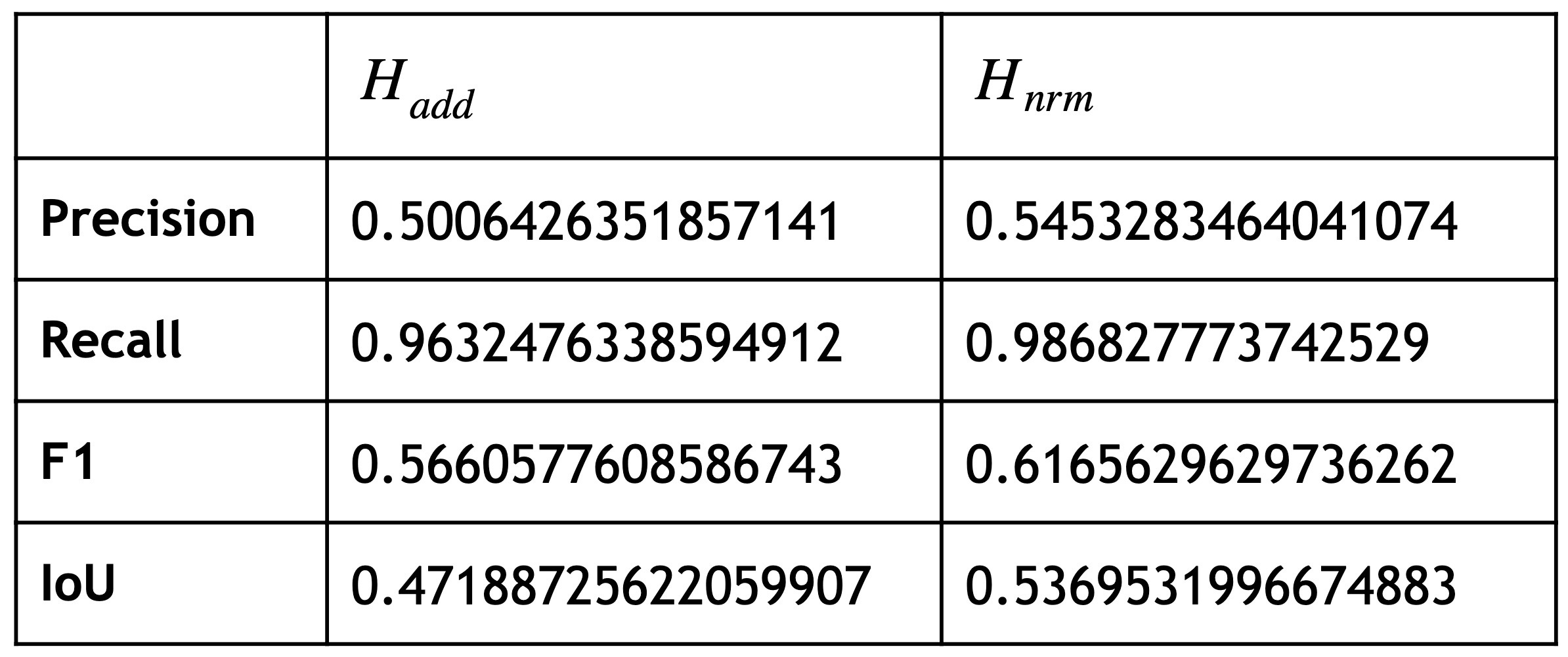
Оптимизация функции 
Синтетические тесты скорости
Чтобы проверить скорость, мы провели другие синтетические тесты. Первый — как зависит время работы алгоритма от количества шотов 
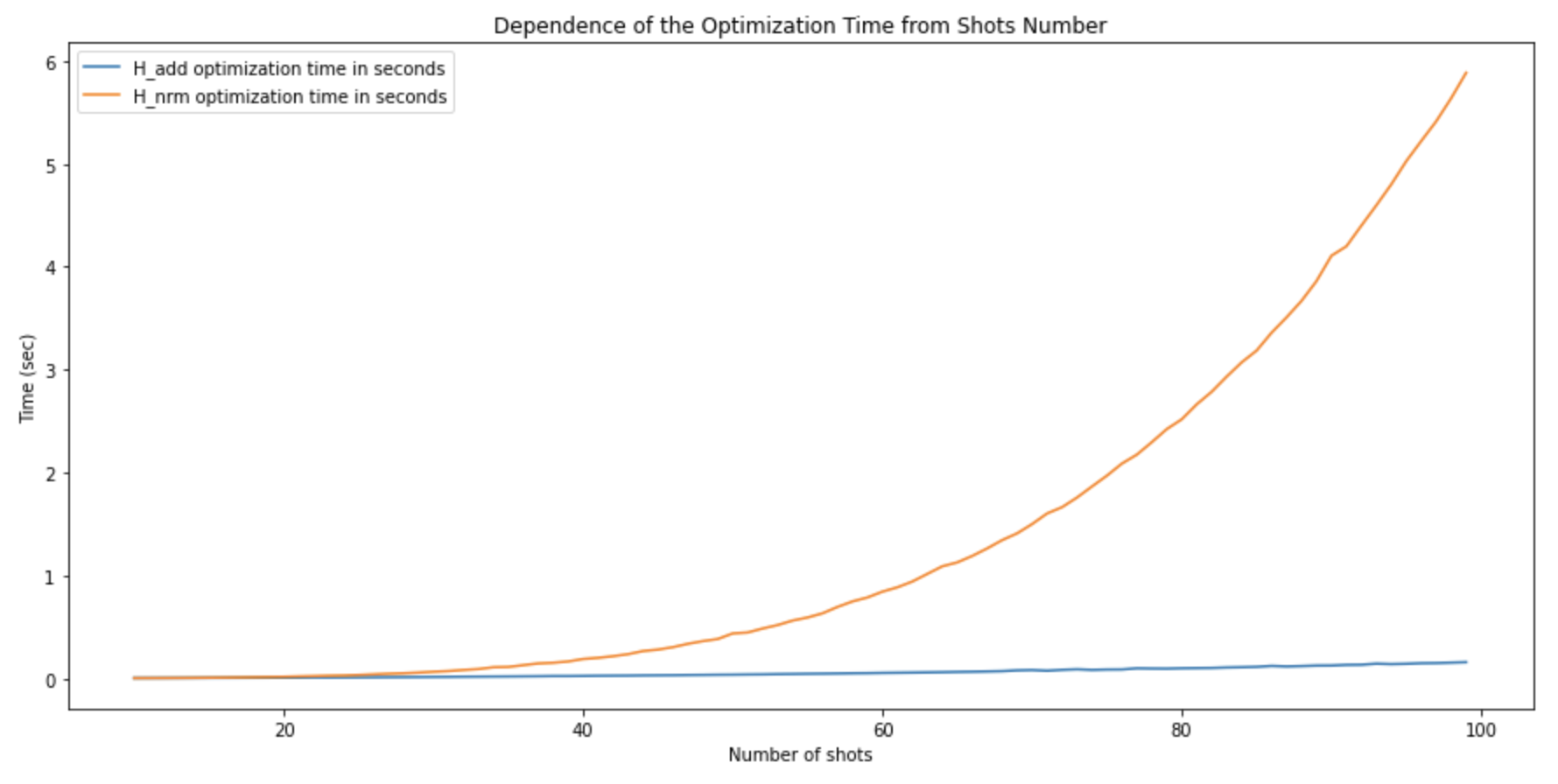
Тест подтвердил теоретическую оценку 




Если зафиксировать количество шотов 






При росте 

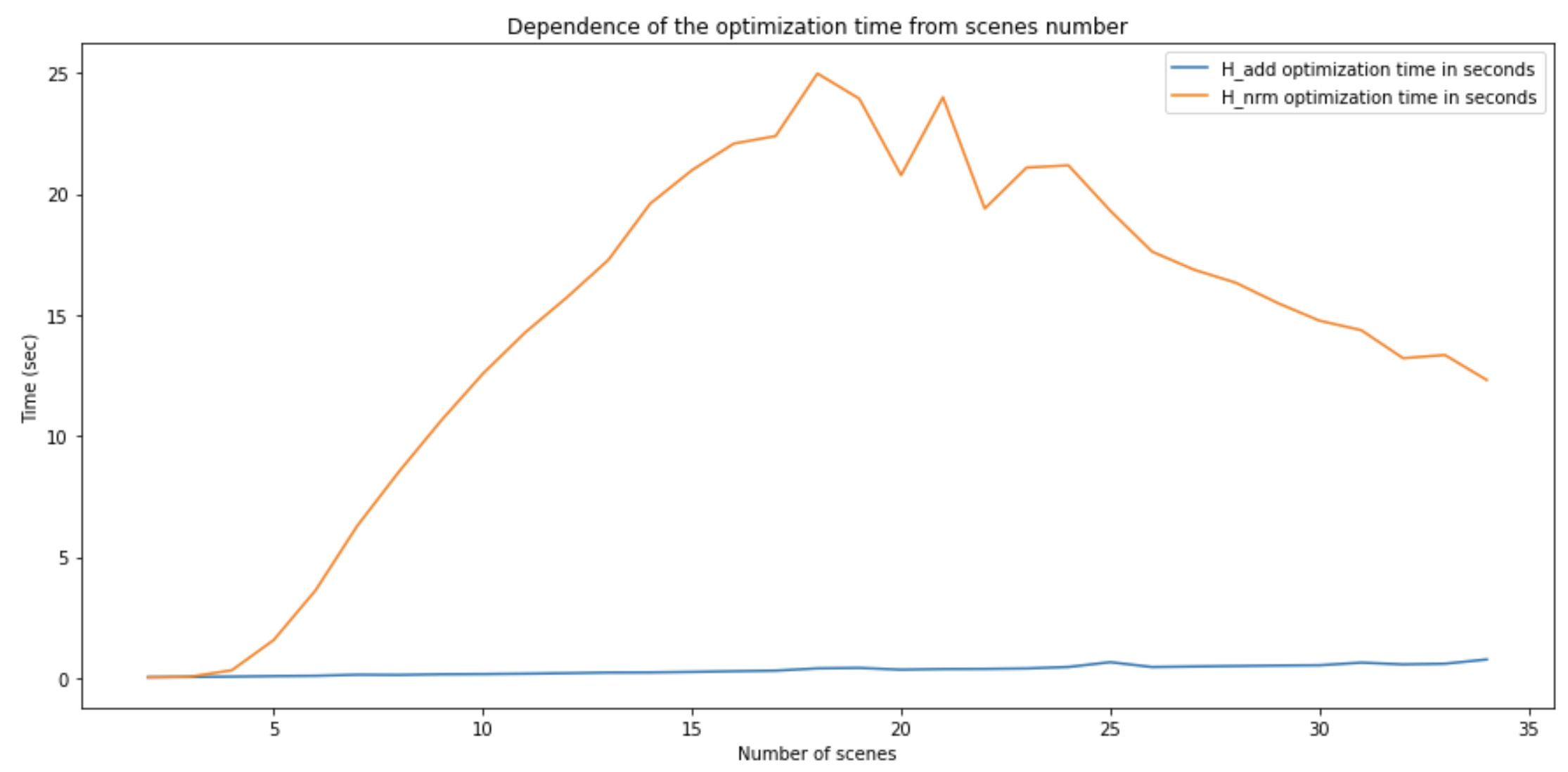
Кажется, это круто, но количество сцен редко будет равно количеству шотов, и всегда будет принимать такое значение, при котором сочетаний много. В уже упомянутых «Мстителях» 2700 шотов и 105 сцен. Количество сочетаний:
Чтобы быть уверенными, что всё поняли правильно и не запутались в нотации оригинальных статей, мы написали письмо Дэниелу Ротману. Он подтвердил, что 

Тесты на реальных данных
Итак, мы выбрали метрику 
Для теста разметили 20 фильмов разных жанров и годов. Разметку делали в пять этапов:
- Подготовили материалы для нарезки:
- отрисовали номера кадров на видео
- напечатали раскадровки с номерами кадров, чтобы можно было охватить взглядом сразу десятки кадров и увидеть границы монтажных склеек.
- Разметчик с помощью подготовленных материалов записал в текстовый файл номера кадров, которые соответствуют границам шотов.
- Затем разделил шоты на сцены. Критерии объединения шотов в сцены описаны выше в пункте «Из чего состоит видео?»
- Готовый файл с разметкой проверили разработчики команды CV. Главная задача при проверке — верифицировать границы сцен, потому что критерии можно трактовать субъективно.
- Проверенную человеком разметку прогнали через скрипт, который нашёл опечатки и ошибки типа «кадр конца шота меньше начала шота».
Вот так выглядит экран разметчика и проверяющего:
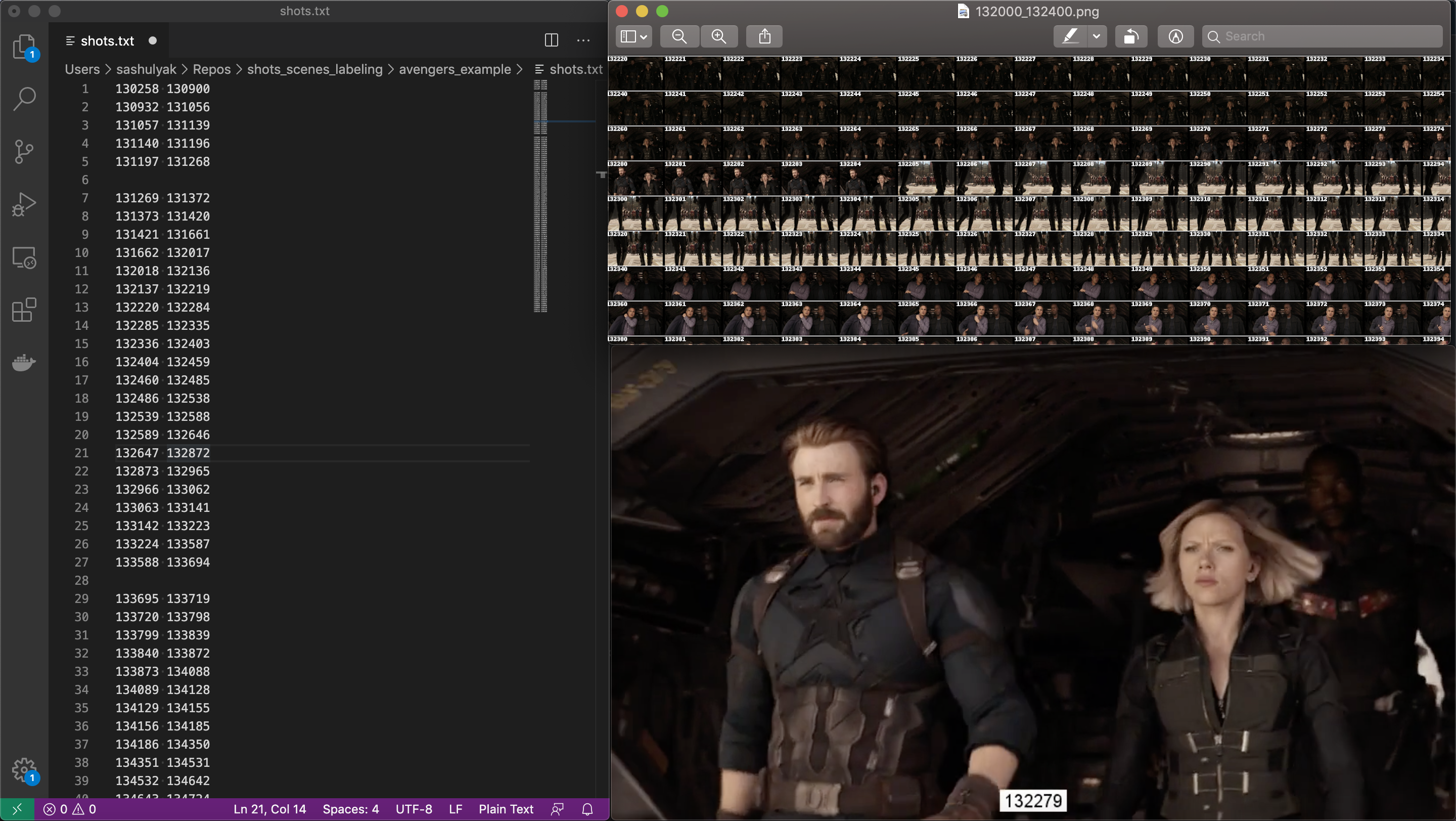
А вот так — разбиение по сценам первых 300 шотов фильма «Мстители: Война бесконечности». Слева истинные сцены, а справа — предсказанные алгоритмом:
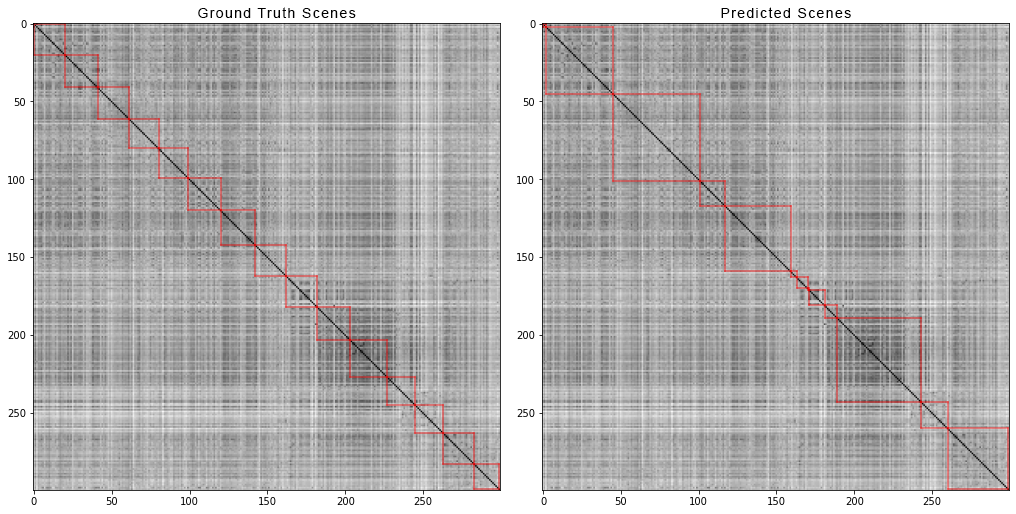
Чтобы получить матрицу попарных расстояний, мы сделали следующее:
- Разделили фильм на 2700 шотов
- Из каждого шота взяли по одному кадру
- Пропустили кадры через нейросеть Xception, обученную на датасете Imagenet, и взяли значения выходов с предпоследнего слоя
- Вычислили попарные Евклидовы расстояния между векторами шотов
Для каждого видео из датасета мы сгенерировали матрицы попарных расстояний и так же, как для синтетических данных, посчитали четыре метрики. Вот какие цифры вышли:
- Precision: 0.4861919030708739
- Recall: 0.8225937459424839
- F1: 0.513676858711775
- IoU: 0.37560909807842874
Ну и что же?
Мы получили бейзлайн, который работает не идеально, но теперь от него можно отталкиваться, пока ищем более точные методы.
Некоторые из дальнейших планов:
- Попробовать другие архитектуры CNN для извлечения признаков.
- Попробовать другие метрики расстояний между шотами.
- Попробовать другие методы оптимизации
, например, генетические алгоритмы.
- Попытаться свести разбиение целого фильма к отдельным частям, на которых
отрабатывает за разумное время, и сравнить, какая будет потеря в качестве.
Код обоих методов и эксперименты на синтетических данных опубликовали на Github. Можно потрогать руками и попробовать ускорить самостоятельно. Лайки и пулл-реквесты приветствуются.
Всем пока, увидимся в следующих статьях!
Автор: Александр Коншин


![Как мы научились делить видео на сцены с помощью хитрой математики - 11 $H_{add}(overline{t})=sumlimits_{для:каждого:квадрата}[сумма:расстояний:внутри:квадрата]tag{1}$](https://www.pvsm.ru/images/2020/04/16/kak-my-nauchilis-delit-video-na-sceny-s-pomoshyu-hitroi-matematiki-11.svg)
![Как мы научились делить видео на сцены с помощью хитрой математики - 12 $H_{avg}(overline{t})=sumlimits_{для:каждого:квадрата}[среднее:расстояние:внутри:квадрата]tag{2}$](https://www.pvsm.ru/images/2020/04/16/kak-my-nauchilis-delit-video-na-sceny-s-pomoshyu-hitroi-matematiki-12.svg)
![Как мы научились делить видео на сцены с помощью хитрой математики - 13 $H_{nrm}(overline{t})=dfrac{sumlimits_{для:каждого:квадрата}[сумма:расстояний:внутри:квадрата]}{sumlimits_{для:каждого:квадрата}[площадь:квадрата]}tag{3}$](https://www.pvsm.ru/images/2020/04/16/kak-my-nauchilis-delit-video-na-sceny-s-pomoshyu-hitroi-matematiki-13.svg)











