Сегодня на конференции в ЦЕРН официально объявили, что каналы распада ZZ и фотон-фотон дают общую достоверность в 5 сигма. Это означает, что преодолен порог между успешной догадкой и научным открытием. Они определенно открыли частицу. В то же время, эксперимент ATLAS более сдержан в своем настроении.
И это отличный момент, чтобы разобраться в том, что мы знаем об этой частице. Лично меня, как студента-физика, интересует разрушение культа Наделения Массой. На этом и сконцентрируемся. Я попробую, насколько это вообще возможно, просто и наглядно объяснить фразу, которую все слышали.
Для этого необхожимо познакомиться с двумя краеугольными камнями теоретической физики — принципом наименьшего действия и теоремой Нётер.
Симметрии
Многие явления современной теории можно объяснить простой конструкцией: наделение Вселенной определенной симметрией — теорема Нётер — известное физическое явление. Несколько примеров:
- пространство однородно — симметрия относительно трансляций — закон сохранения импульса
- время однороно — симметрия относительно перемещений во времени — закон сохранения энергии (на самом деле, тот же закон, что и с импульсом)
- пространство изотропно — симметрия относительно вращений — закон сохранения момента импульса (с этого момента можно ездить на велосипеде)
- чуть сложнее: если принять, что теория симметрична относительно локальных калибровочных преобразований — в несколько шагов можно получить свет, электричество и все блага цивилизации
Пользуясь тем же принципом, мы можем подобрать набор симметрий и получить систему, которой соответствует современная Стандартная модель. Но тогда мы получим 4 калибровочных бозона — фотон, W± и Z, которые не будет иметь массы.
В то же время на эксперименте мы однозначно наблюдаем 1 безмассовый (фотон) и 3 довольно тяжелых частицы.
Здесь важно понять, что в физике множество явлений сильно меняются внешне, в зависимости от того, как мы их рассматриваем — но при этом разные «представления» все равно описывают одно и то же явление. В квантовой физике вообще тяжело говорить о каких-то частицах или состояниях — свойства сильно зависят от базиса, по которому мы их раскладываем. Вспомним, хотя бы, осцилляции каонов.
Спонтанное нарушение симметрии
Перейдем конкретно к Наделению Массой. Простейший способ понять, почему мы предсказываем безмассовые частицы, а меряем — массивные, состоит в механизме спонтанного нарушения симметрии в системе. Для понимания этого механизма необходимы базовые знания в классической механике (у нас в университете ее изучают на 2 курсе) — я не могу на это рассчитывать, потому буду обходиться без формул.
Отвлечемся и рассмотрим простейшую механическую систему: цилиндр из какого-то однородного материала, размещенный вертикально, на основания которого мы будем давить. Какое-то время все будет идти хорошо: цилиндр симметричен и он постепенно становится короче под давлением. Но в какой-то момент напряжения внутри цилиндра вырастут настолько, что ему станет невыгодно уплотняться по длине — состояние, в котором цилиндр согнулся в сторону, становится предпочтительным и система стремится к нему.
В этот момент возникает вопрос: в какую сторону выгнуться цилиндру? Все направления одинаковы и цилиндр начинает напоминать античного осла, который умер, выбирая между двумя одинаковыми стогами сена. С другой стороны, система обязана занять какое-то положение — и оно не произвольно, но зависит от куда более сложной динамики системы. Для нас же, рассматривающих систему кинематически — выбор будет произвольным, спонтанным.
Если рассмотреть это на языке математики, получим следующую картинку:
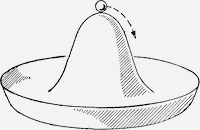
Это график энергии системы, а шарик символизирует текущее ее состояние. Эквивалентной этой системе будет еще более простая: безмассовая частица в потенциале, что имеет форму ровно, как на изображении выше. Но мы рассмотрим еще более простую систему — частицу в одном измерении на одном центральном сечении этого графика:
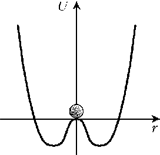
Сейчас мы увидим, как она приобретает массу. Начинаются формулы. Классическая механика, 2 курс. Первый том Ландау, если угодно :)
Лагранжиан системы:
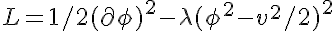
Первое слагаемое — кинетическое, второе — соответствует потенциалу, в котором находится частица. Но все волшебным образом меняется, если мы изменим систему отсчета. Переместим 0 системы в один из минимумом потенциала — спонтанно нарушим симметрию. Фактически, мы принимаем, что система скатилась в какой-то определенный минимум. Тогда она выглядит вот так:
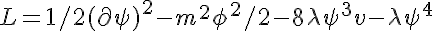
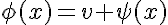
Что мы видим? Благодаря замене переменных в системе выделилось слагаемое, в котором мы можем интерпретировать, как массу нашей частицы. Тем не менее, на самом деле, не произошло ничего сверхъестесственного. Мы просто изменили, если угодно, точку зрения — отошли на 3 шага влево.
Выводы
Подобным образом — только в значительно более усложненном виде — мы можем увидеть, что существовавшая недавно неполная Стандартная модель может стать не только самосогласованной на практике, но и согласующейся с куда более общей теоретической конструкцией.
Замечу: бозон Хиггса можно рассматривать и без всего вышенаписанного. Если забыть о симметриях, бозон Хиггса становится просто частицей, благодаря существованию которой эксперимент сходится с теорией.
Тем не менее, это не умаляет достижения. Сегодня мы получили подтверждение одной из наиболее удачных догадок в теоретической физики.
Вот так я представляю себе простейшее объяснение этого интересного фокуса. Всем хорошего дня, не ведитесь на популизм!
Автор: ckald






