В двух предыдущих статьях я по касательной затронул проблему, которую назвал проблемой «двух и более учителей»:
1. Модель функционального разделения сознания и бессознательного. Введение
2. Модель проявления сознания или ИНС без эффекта забывания
Теперь хотелось бы с ней разобраться более подробно. Это сложная и еще в принципе не решенная теоретическая проблема из области искусственного интеллекта. Четко её сформулировать у меня не получается, а не то, чтобы решить. Но я с ней постоянно встречаюсь в разных задачах, и все время об неё спотыкаюсь. Эти предыдущие статьи могли показать её важность с точки зрения понимания того, что есть сознание. Но это все же лирика. А здесь я хотел бы говорить более технически.
Тут я покажу, как я впервые встретился с этой проблемой еще начиная с 2006 года, но теперь точно такая же проблема явно видна и при решении биоинформационной задачи сворачивания РНК (про это я тоже написал серию статей, последняя в которой есть все ссылки ). Внешние описание этих задач существенно разное, но в этом и прелесть — проблема возникает не зависимо от задачи, и кажется есть важный аспект, который просто надо уметь решать говоря об интеллектуальных методах.
Было время, когда я был фанатом игры в Цивилизацию. Надо сказать, что её первые версии были наиболее интеллектуальны, а в версии после Civilization II: Test of Time можно вообще не играть — они испортили важную интеллектуальную начинку. Поэтому совсем не удивительно, что ниже я предложу компьютерно сыграть в этюд по этой игре.
Важно отметить, что устраивают турниры с подобными сценариями, например, ICFPC 2012 с краудсорсингом и нейронными сетями, играя в игру Supaplex. Это тоже интересная задача, но в ней не возникает проблемы «двух и более учителей». Поэтому цель этой статьи понять когда же эта проблема возникает.
Правила игры
Модельная среда представляет собой карту местности, разделенную на 276 квадратов (участков) различного типа – луг, равнина, океан, река и т.д. (всего 16 видов). На рисунке 50 ход при моделировании. Красный квадратик — «Центр города», желтый квадратик — «поселенец», зеленых крестик — «житель»
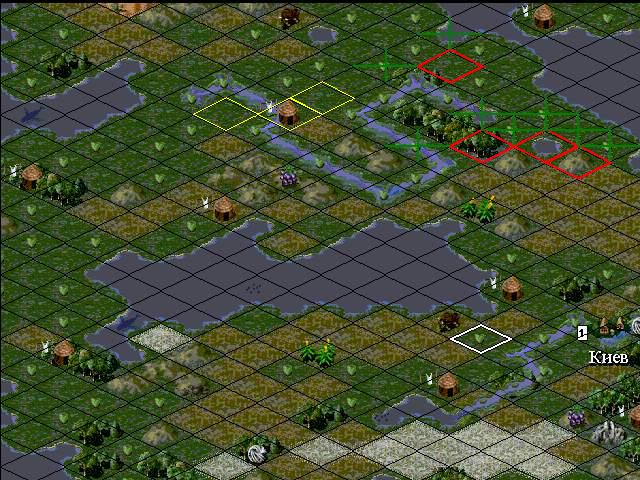
Каждый тип территории отличается количеством ресурсов, которые можно получить, обрабатывая эту территорию. Различают три вида ресурсов – пища, металл, деньги. В таблице показаны все классы и их характеристики.
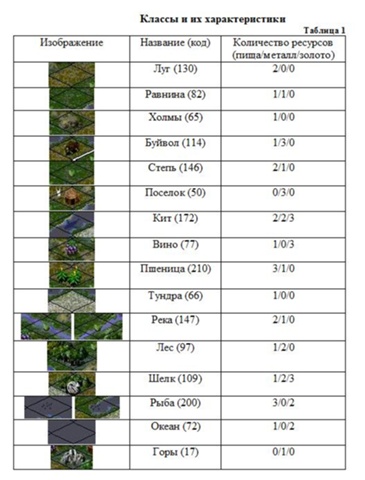
Игра начинается с одного поселенца, который помещается в случайную позицию на карте. Задача поселенца выбрать место для будущего города, необходимого для того, чтобы обрабатывать местности на карте. Видимость карты для поселенца составляет 25 квадратов (радиус 2 квадрата вокруг него).
Сделав свой выбор, поселенец строит город, а сам пропадает – превращается в одного жителя города. Город занимает площадь 9 квадратов (радиус 1 квадрат вокруг него), потенциальных для выбора места обработки. Центр города считается всегда обрабатываемым. Окраины (8 квадратов) могут обрабатываться жителями, на одного жителя – один квадрат. Выбор делается статично в момент появления жителя. Таким образом, сразу после постройки выбирается место для обработки. Далее при накоплении на складах города определенного количества еды – появляется житель города (и стоит задача выбора места обработки), а при накоплении определенного количества металла — появляется новый поселенец (и стоит задача выбора места для нового города).
Количество необходимой еды для появления нового жителя зависит от размера города (числа жителей этого города). При одном жителе нужно 20 ед. Еды, при двух – 30 ед. и т.д. Количество металла необходимое для создания поселенца 40 ед.
Задача состоит в выборе стратегии при которой за 80 ходов можно добыть наибольшее количество денег.
Учитель
Обучение учителем направленно на то, чтобы агент мог хоть как то рационально вести себя в среде. Такое рациональное поведение может оказаться выгодным при равномерном распределении ресурсов по территории карты, а так же при примерно одинаковой важности каждого из ресурсов. Это происходит от того, что учитель обучает агента оценивать каждое из 8 перемещений в соответствии с методом взвешенной оценки альтернатив.
А именно, из 8 альтернатив по каждому ресурсу находится максимальное и минимальное значение ресурсов суммированное по всей площади города. Значения всех ресурсов приводятся к одному масштабу
(Value_i — min/maxmin)*255, где maxmin — разница между максимумом и минимумом среди 8 альтернатив данного ресурса. Полученные значения и есть оценки.
Проблема как она есть
Обучение учителя агент может со временем изменить. Но как? На основании чего? Собственно, желательно по факту выигрыша в очередной партии из 80 ходов, т.е. когда набирается большие число денег. Но как это зафиксировать? Тут возникает проблема — как описать всю эту последовательность из 80 ходов, со всеми возможными состояниями. И оказывается это не возможно, уж слишком большое надо иметь представление. Да, и на самом деле это сильно излишнее. Оказывается надо иметь несколько простых стратегий, чтобы выигрывать.
Ну для примера. В принципе эта задача просчитывается… если знать что она длится 80 ходов, если знать при каком условии появляется новый житель в городе и поселенец, если знать какие типы территорий существуют и сколько на каждой из них ресурсов, и главное по какому параметру оценивается успех. То при всей прочей неопределенности задача жестко просчитывается и по крайней мере можно написать алгоритм, который это рассчитывает.
Для вырожденного случая когда есть всего два типа территорий — Океан (1/0/2) и Степь (1/1/0) — стратегия следующая: имеет смысл устанавливать цель города — получение поселенца (степь+степь), только тогда когда до середины игры он сможет предоставить 2-х и более поселенцев. По прошествию 25% игры следует использовать смешенную стратегию (степь+океан), а после 50% пройденной игры наращивать только объем золота (тип города океан+океан). Вырожденность заключается в том, что здесь города не растут, т.к. прирост пищи только 2 ед., что равно ее расходу на одного жителя (напомню, что центр города обрабатывается без жителя). В итоге — получаем 484 ед. золота… и ни какая другая стратегия не позволяет улучшить показатель.
По сути каждая из таких тактических стратегий — есть другая функция пригодности. Вот и получается, что имея полученную от учителя базовую тактическую стратегию, нужно найти такие параметры, которые позволят сформировать определенную тактическую стратегию. И уже по ходу игры менять эти стратегии.
в общем виде получается сложно. Упрощая надо понять, что любая найденная успешная стратегия (эвристика) — есть не что иное как другая функция пригодности. Т.е. это по сути другой «учитель». А вот проблема обучения от двух и более учителей — согласовать две пригодные тактические стратегии в одну.
Не знаю на сколько мне удалось описать понятно проблему… но пишите что не ясно, помогайте, кто соизволит вникнуть в проблематику.
В следующей части я попробую описать эту же проблему в задаче сворачивания РНК, что будет уже не «игрушечной проблемой». Но чисто предметно будет сложнее, но зато сам вид тактических стратегий будет проще.
У меня стоит цель сделать из этого понятную математическую проблему, которая бы не объяснялась бы через прикладные задачи — но как то пока сложновато. Жду помощи.
Автор: tac






