Визуализация границ решения классификатора на основе изображений

Введение

Понимание того, как классификатор разбивает исходное многомерное пространство признаков на множество целевых классов, является важным шагом для анализа любой задачи классификации и оценки решения, полученного с помощью машинного обучения.

Современные подходы к визуализации решений классификаторов в основном либо используют диаграммы рассеивания, которые могут отображать лишь проекции исходных обучающих выборок, но явно не показывают фактические границы принятия решений, либо используют внутреннее устройство классификатора (например kNN, SVM, Logistic Regression) для которых легко построить геометрическую интерпретацию. Такой способ не подойдет для визуализации, например, нейросетевого классификатора.

В статье "Image-based Visualization of Classifier Decision Boundaries" (Rodrigues et al., 2018) предлагается эффективный, красивый и достаточно простой альтернативный метод для визуализации решений классификатора, который лишен вышеописанных недостатков. А именно метод подходит для классификаторов любого вида и строит границы принятия решений с помощью изображений с произвольной частотой дискретизации.

Этот пост — краткий обзор основных идей и результатов из оригинальной статьи.

Описание метода

Основу метода составляет обратное семплирование (англ. upsampling) из плоскости изображения , которое представляется набором пикселей, в пространство признаков .

Для работы метода необходимы два отображения — прямая проекция из пространства признаков в плоскость изображения и обратная . В качестве таких отображений используются LAMP (Joia et al. 2011) и iLAMP (Amorim et al. 2012), соответственно.

Построение

Чтобы построить изображение необходимо присвоить цвет каждому пикселю. Для этого для каждого пикселя найдем точек из исходного гиперпространства, где — параметр, задающийся пользователем. Пусть пиксель уже имеет реальных прообразов из обучающей выборки. Тогда равномерно выберем оставшихся точек с поверхности пикселя и найдем для них прообраз через обратную проекцию . Таким образом цвет каждого пикселя будет обусловлен как минимум точками исходного пространства, и все изображение будет закрашено.

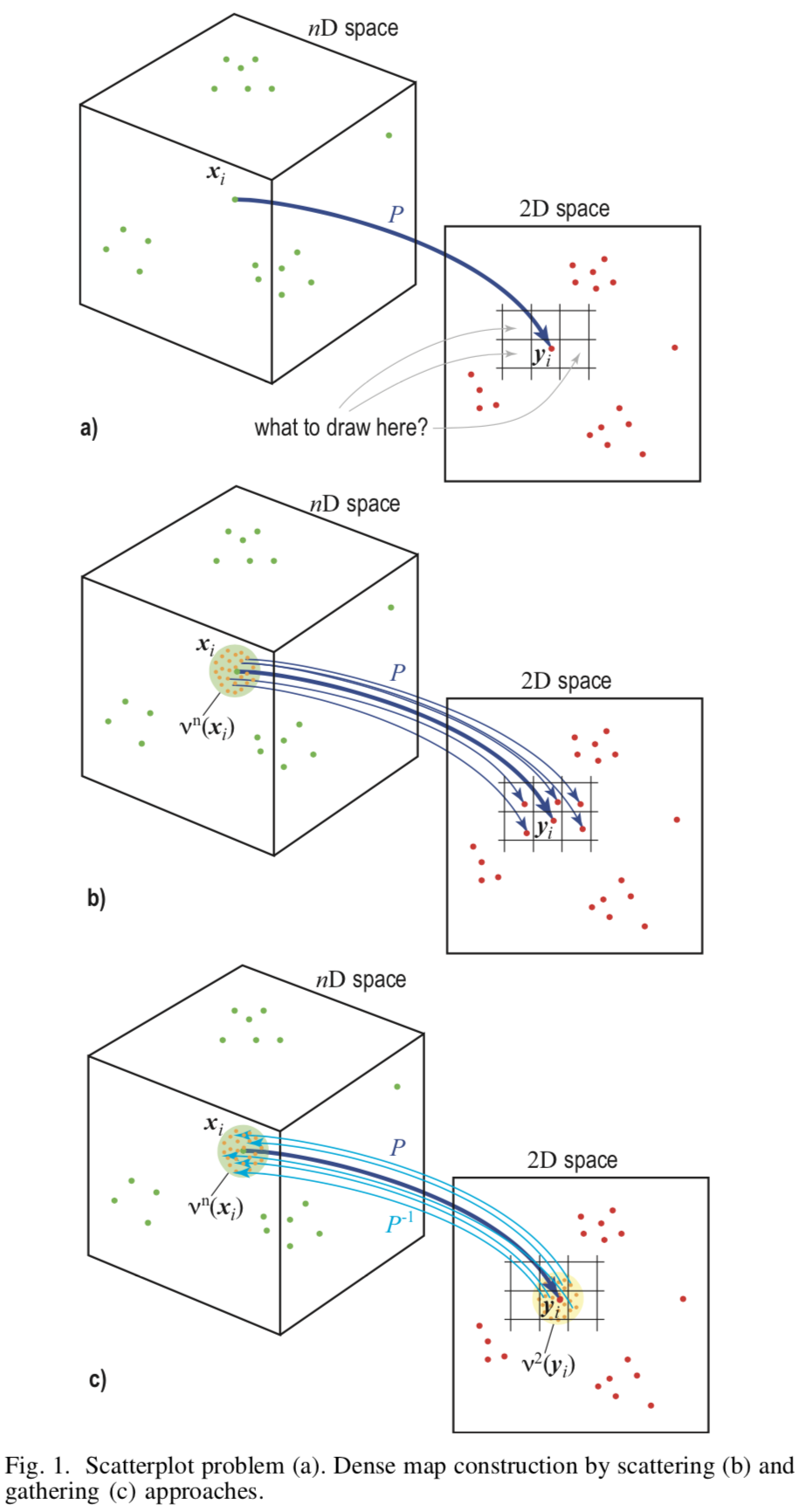
[Рис.1] Схематическое изображение разных подходов

Определение цвета

Цвет каждого пикселя определяется голосованием большинства для меток классов соответствующих прообразов.

где — множество всех классов, — классификатор.

Каждому классу поставим в соответствие некоторый тон (англ. hue) — если в проекции есть точки из реальной выборки, и немного измененный тон для пикселей в которых оказались только синтетические точки.

Смешение

Определим смешение пикселя (от англ. confusion) — как отношение числа меток превалирующего класса к общему числу прообразов пикселя :

Высокое значение говорит о согласованности классификатора, тогда как низкое значение сигнализирует о приближении к разделяющей границе. Информация о смешении кодируется в насыщенность пикселя — чем выше согласованность, тем выше насыщенность.

Плотность

Несмотря на то, что были сгенерированы минимум точек прообразов для каждого пикселя, могут остаться пиксели для которых существует гораздо больше реальных точек из обучающей выборки. Такие пиксели должны быть учтены при визуализации. Для этого введем плотность пикселя как число его точек прообразов из . Можно было бы использовать эту плотность напрямую для определения яркости пикселя как , но авторы статьи указывают на то что, это не дает желаемого результата, т.к. некоторые тона получаются заведомо темнее чем другие. Поэтому используется более хитрая настройка одновременно насыщенности и яркости через нормализованный параметр плотности.

Тогда, если — яркость линейно зависит от параметра в пределах . При начинает линейно расти насыщенность от до .

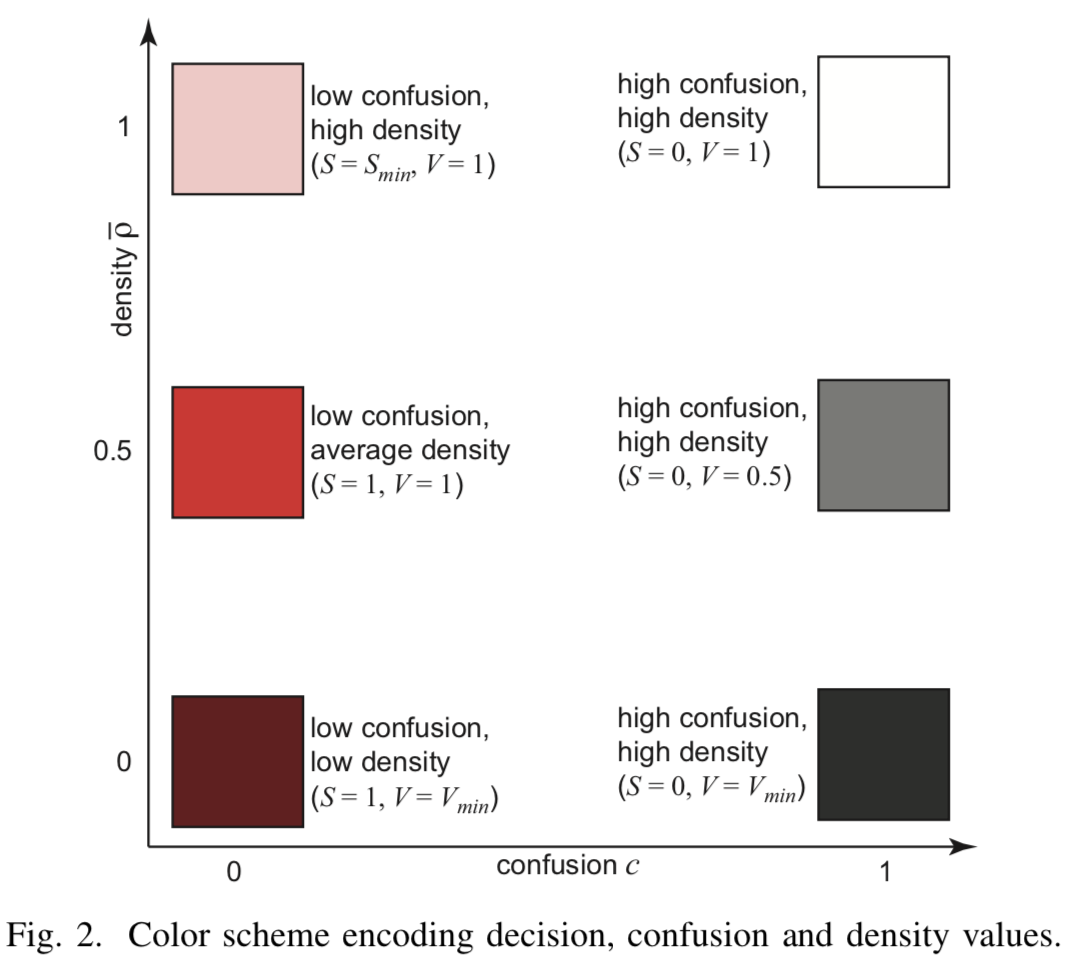
[Рис.2] Цветовое кодирование

Эксперименты и результаты

Для экспериментов решались задачи бинарной классификации на наборе изображений цифр MNIST и многоклассовой классификации на наборе The Image Segmentation Dataset, который содержит 2310 изображений, поделенных на 7 классов. Для каждого изображения имеется 19 признаков.

Результаты визуализации при различных параметрах разрешения и минимального числа прообразов для бинарного классификатора LogisticRegression на MNIST изображены на рисунке [3]. Классы разделяются прямой с высокой точностью и алгоритм визуализации отлиично справляется. При увеличении разрешения, облака исходных точек почти полностью растворяются среди множества сгенерированных точек.

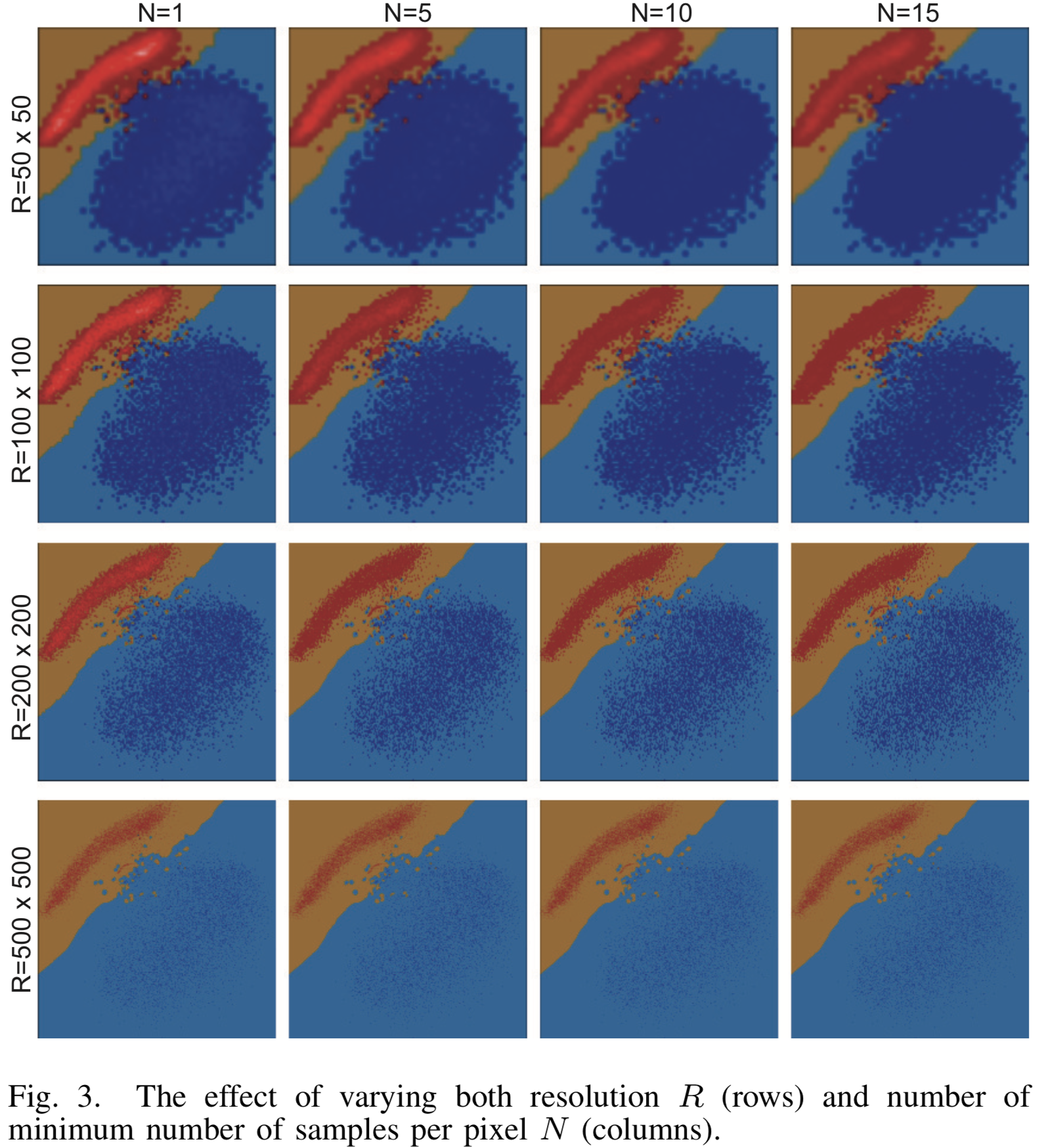
[Рис. 3] Результат визуализации для различных параметров разрешения и минимального числа семплов N для класссификатора LogisticRegression

Визуализация при для трех различных классификаторов для мульти-классификации на рисунке [4]. Проекции исходных точек сильно перемешаны, и построить явные разделяющие границы в местах скопления проекций тестовых примеров не представляется возможным. Однако, в стороне от основного скопления получились явные границы классов, информация о которых не отображена на обычных проекциях, но получается только при помощи синтетических точек.

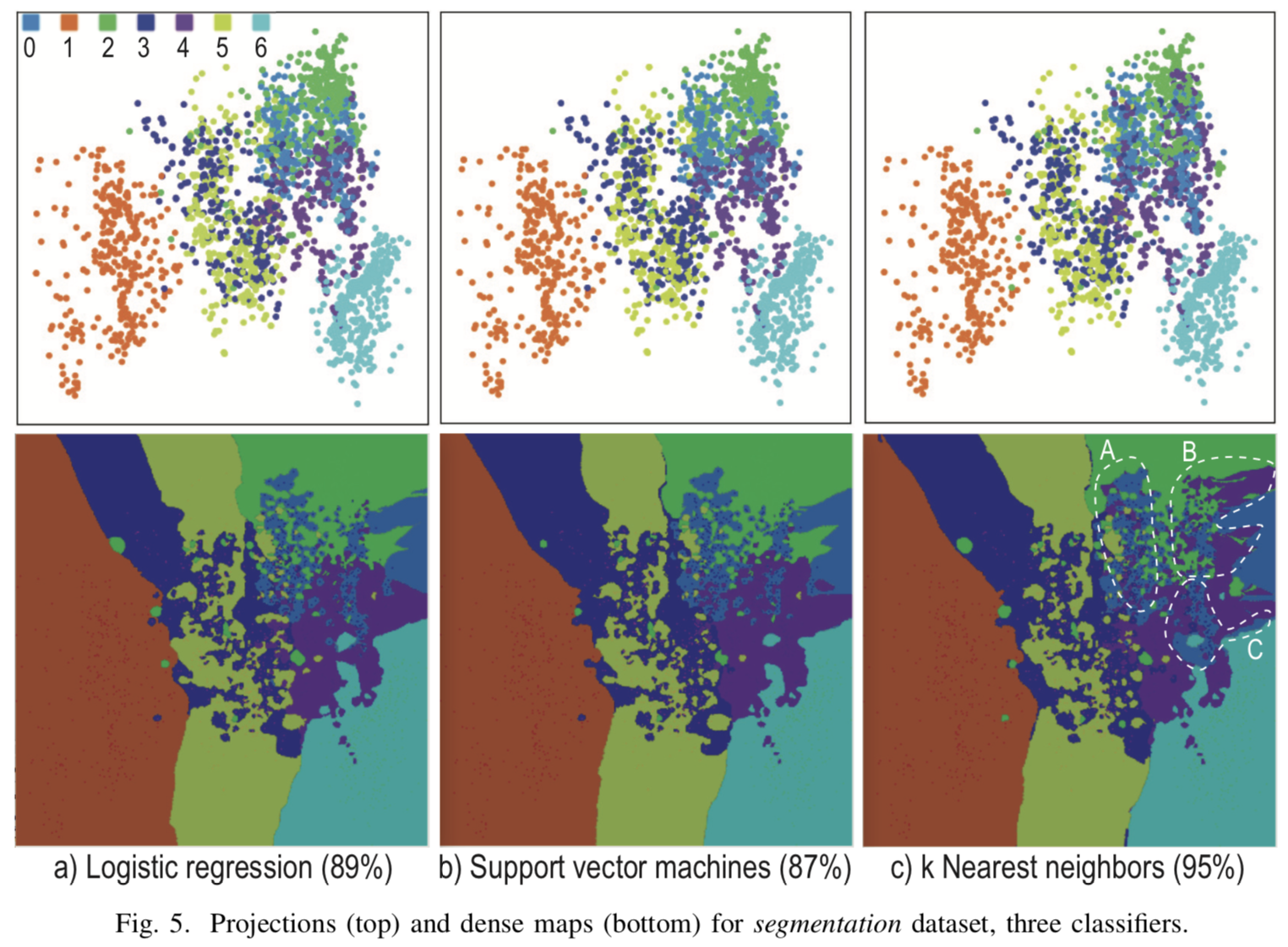
[Рис. 4] Результат визуализации трех различных классификаторов для k=7, R=500x500, N=5

Заключение

Визуализация границ классов может быть использована при построении и отладке решающего алгоритма, при подборе гиперпараметров, при борьбе с переобучением, для представления и анализа результатов.

Описанный авторами оригинальной статьи метод может применяться для любых задач классификации, где данные представимы в виде набора признаков фиксированный размерности. В отличие от других алгоритмов визуализации, данный подход может применяться для любых, сколь угодно сложных классификаторов и для наборов данных с произвольным числом примеров, даже с очень небольшим, т.к. даже при малом алгоритм работает стабильно, не сильно теряя в качестве.

Автор: Зотов Алексей

Источник