Перенормировка, возможно, оказалась самым важным прорывом в теоретической физике за последние 50 лет

Не нужно анализировать поведение отдельных молекул воды, чтобы понять поведение капель, или анализировать капли, чтобы понять волны. Возможность переключать фокус между разными масштабами – это и есть суть перенормировки
В 1940-х годах физики-первопроходцы наткнулись на новый слой реальности. Место частиц заняли поля – всеобъемлющие и волнующиеся сущности, заполнявшие всё пространство на манер океана. Одна небольшая рябь в таком поле могла обозначать электрон, другая – фотон, а их взаимодействия, судя по всему, могли объяснить все электромагнитные явления.
Была только одна проблема – вся эта теория держалась на надеждах и молитвах. Только при помощи такой техники, как "перенормировка", позволявшей тщательно скрывать бесконечные величины, исследователи могли обойти бессмысленные предсказания этой теории. Схема работала, но даже те, кто разрабатывал эту теорию, подозревали, что она может оказаться карточным домиком, держащимся за счёт извращённого математического трюка.
«Я назвал бы это ''чокнутым процессом'', — писал позднее Ричард Фейнман. – Нам пришлось опуститься до подобных фокусов, из-за чего мы не смогли доказать, что теория квантовой электродинамики математически непротиворечива».
Оправдали теорию позже, через несколько десятилетий, и благодаря вроде бы не связанной с нею области физики. Исследователи, изучавшие намагничивание, обнаружили, что перенормировка – это вообще не про бесконечности. Эта теория касается разделения вселенной на царства независимых размеров. И такая перспектива сегодня управляет многими уголками физики.
Дэвид Тонг, теоретический физик из Кембриджского университета, пишет, что перенормировка – «это, возможно, самый важный прорыв в теоретической физике за последние 50 лет».
Повесть о двух зарядах
С какой-то точки зрения теории поля представляют собой самые успешные теории в науке. Теория квантовой электродинамики (КЭД), один из столпов Стандартной модели физики частиц, дала теоретические предсказания, совпадающие с экспериментами с точностью до миллиардных долей.
Но в 1930-х и 1940-х годах будущее теории не было столь определённым. Аппроксимация сложного поведения полей часто выдавало бессмысленные, бесконечные по величине ответы, из-за чего некоторые теоретики решили, что теории поля – это тупиковый путь.
Фейнман и другие начали искать новые перспективы – возможно, такие, которые вернут на сцену частицы – но вместо этого нашли один трюк. Они обнаружили, что уравнения КЭД дают приемлемые предсказания, если применить к ним загадочную процедуру перенормировки.
Упражнение выглядит примерно так. Если вычисления КЭД выдают бесконечную сумму, обрежьте её. Превратите ту часть, которая хочет устремиться в бесконечности, в фиксированный коэффициент, стоящий перед суммой. Замените его конечным измерением, сделанным в лаборатории. Наконец, позвольте исправленной сумме устремиться к бесконечности.
Для некоторых физиков такой рецепт напоминал игру в скорлупки. «Это просто нельзя назвать осмысленной математикой», — писал выдающийся квантовый теоретик Поль Дирак.
Суть проблемы – и первый шаг к появившемуся позже решению – заключается в том, как физики работают с зарядом электрона.
В описанной схеме электрический заряд происходит от коэффициента – значения, проглатывающего бесконечность в процессе математической перетасовки. Теоретикам, терявшимся в догадках касательно физического смысла перенормировки, КЭД намекала о существовании у электрона двух зарядов: теоретического, бесконечно, и измеряемого, конечного. Возможно, в ядре электрона заряд бесконечен. Но на практике влияние квантового поля (которое можно представить себе, как виртуальное облако положительно заряженных частиц) окутывает электрон так, что экспериментаторы измеряют только скромный суммарный заряд.
Два физика, Марри Гелл-Ман и Фрэнсис Лоу, оформили эту идею в 1954. Он связали два заряда электрона с одним «эффективным» зарядом, изменяющимся с расстоянием. Чем ближе вы подбираетесь (чем глубже проникаете в положительное облако электрона), тем больше заряда вы видите.
Их работа впервые связала перенормировку с идеей масштабов. Из неё можно было сделать вывод, что квантовые физики нашли правильный ответ на неправильный вопрос. Вместо того, чтобы беспокоиться о бесконечностях, им надо было заниматься объединением крохотного с огромным.
Перенормировка – это «математический вариант микроскопа», сказала Астрид Эйкхорн, физик из Университета Южной Дании, использующая перенормировку для поисков теорий квантовой гравитации. «И наоборот, можно начать с микроскопической системы и уменьшить масштаб. Это комбинация микроскопа с телескопом».
Магниты спасают ситуацию
Вторая подсказка возникла из мира конденсированных состояний материи, где физики удивлялись, как грубая модель магнита смогла точно предсказать тонкие детали определённых преобразований. Модель Изинга представляла собой всего лишь сетку из атомных стрелок, каждая из которых может указывать только вверх или вниз – и, тем не менее, она предсказывала поведение настоящих магнитов с немыслимой точностью.
При низких температурах большинство атомов выстраиваются в ряды, что намагничивает вещество. При высоких температурах наступает беспорядок, и решётка размагничивается. Но в критической точке перехода существуют островки выровненных атомов разнообразных размеров. Что важно, распределение определённых величин в этой критической точке получается одинаковым что в модели Изинга, что в реальных магнитах различных материалов, что в не связанных с магнитами системах, вроде перехода при высоком давлении, когда вода становится неотличимой от пара. Открытие этой т.н. универсальности было настолько же странным, как открытие того, что максимальная скорость слонов и белых цапель в точности совпадает.
Физики обычно не работают одновременно с объектами различных размеров. Однако это универсальное поведение в районе критической точки заставило их заниматься длинами всех масштабов сразу.
Лео Каданов, исследователь конденсированных состояний материи, в 1966 году придумал, как с этим справиться. Он разработал технику «разбиения спинов на блоки». Решётка Изинга, слишком сложная, чтобы работать с ней напрямую, разбивалась на блоки скромного размера по нескольку стрелок на каждую из сторон. Он подсчитывал среднюю ориентацию группы стрелок, и заменял весь блок этим значением. Повторяя процесс, он сглаживал мелкие детали сетки, уменьшая масштаб с тем, чтобы понять общее поведение системы.
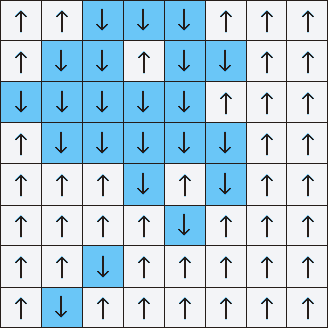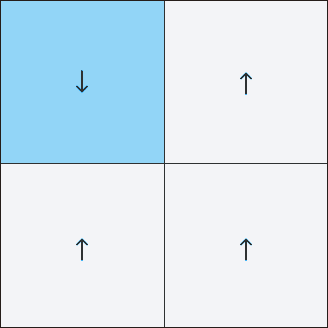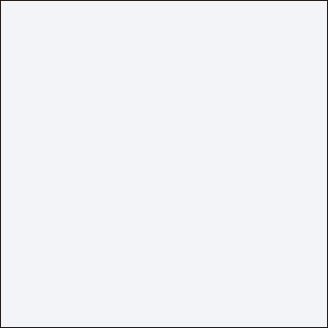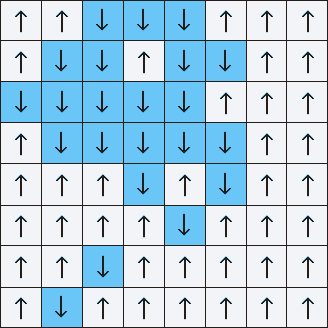
Блочная перенормировка спинов усредняет сетку со множеством отдельных спинов, превращая их в блоки всё возрастающего размера
Наконец, Кен Уилсон – бывший студент Гелл-Мана, занимавшийся сразу физикой частик и конденсированными состояниями – объединил идеи Гелл-Мана и Лоу с идеями Каданова. Его "ренормализационная группа", впервые описанная им в 1971, оправдала извращённые подсчёты КЭД и предоставила лестницу масштабов для универсальных систем. Эта работа обеспечила ему нобелевскую премию и навсегда изменила физику.
Пол Фендли, специалист по конденсированным состояниям из Оксфордского университета, считает, что лучше всего представить концепцию ренормализационной группы Уилсона как «теорию теорий», объединяющую микроскопическое с макроскопическим.
Возьмём магнитную решётку. На микроскопическом уровне легко написать уравнение, связывающее две соседних стрелки. Однако будет практически невозможно экстраполировать эту формулу на триллионы частиц. Вы берёте не тот масштаб.
Ренормализационная группа Уилсона описывает преобразование теории строительных блоков в теорию структур. Вы начинаете с теории небольших кусочков, допустим, атомов бильярдного шара. Покрутите ручку математического аппарата Уилсона, и получите связанную с этим теорию, описывающую группы этих кусочков – например, молекул бильярдного шара. Крутите дальше, масштаб уменьшается, и объёмы групп всё растут – появляются скопления молекул, сектора бильярдного шара, и т.д. В итоге можно будет подсчитать что-нибудь интересное – к примеру, путь всего шара целиком.
Такова магия ренормализационной группы: она помогает определить, какие величины будет полезно измерить, а какие сложные микроскопические детали можно игнорировать. Сёрфера интересует высота волн, а не толкотня молекул воды. В субатомной физике перенормировка говорит физикам, когда они могут работать с относительно простым протоном вместо спутанного клубка его внутренних кварков.
Ренормализационная группа Уилсона также дали основание предполагать, что напасти Фейнмана и его современников происходили от попыток понять электрон, находясь к нему бесконечно близко. «Нельзя ожидать, что теории будут работать на любых, сколь угодно малых масштабах расстояний», — сказал Джеймс Фрэзер, философ физики из Даремского университета Британии. Теперь-то физики понимают, что обрезание сумм и тасовка бесконечностей – это правильный способ вести подсчёты, когда у вашей теории есть минимальный размер решётки. «Отрезание лишнего компенсирует наше незнание того, что происходит на нижних уровнях», — сказал Фрэзер.
Иначе говоря, КЭД и Стандартная модель просто не способны сказать, каким будет заряд электрона на расстоянии в ноль нанометров. Такие теории физики называют «эффективными». Лучше всего они работают на хорошо определённых расстояниях. Основная задача физики высоких энергий – выяснить, что происходит, когда частицы сближаются ещё сильнее.
От большого к малому
Сегодня «чокнутый процесс» Фейнмана используется в физике не реже алгебры, а его применение ответственно как за величайшие успехи в этой области, так и за текущие вызовы. Во время перенормировки сложные субмикроскопические тонкости обычно исчезают. Возможно, они и существуют, но на общую картину не влияют. «Простота – это благо, — сказал Фендли. — Есть в этом что-то божественное».
Этот математический факт описывает тенденцию природы разделяться на независимые по большей части миры. При разработке небоскрёба инженеры игнорируют отдельные молекулы стали. Химики анализируют молекулярные связи, оставаясь в блаженном неведении по поводу кварков и глюонов. Разделение явлений по линейным размерам, численно выраженное в ренормализационных группах, позволило учёным с течением столетий постепенно переходить от большого к малому, вместо того, чтобы атаковать все размерности одновременно.
И всё же в то же время враждебность перенормировки к микроскопическим деталям работает против современных физиков, страстно желающих обнаружить признаки следующего масштаба микромира. Из принципа разделения масштабов следует, что им придётся копать поглубже, чтобы преодолеть склонность природы к сокрытию мелких деталей от таких любопытных великанов, как мы.
«Перенормировка помогает нам упростить задачу, — сказал Натан Сейберг, физик-теоретик из Института передовых исследований в Принстоне. – Однако она также прячет происходящее на коротких дистанциях. Сразу всё получить нельзя».
Автор: Вячеслав Голованов



