Метод покоординатного спуска является одним из простейших методов многомерной оптимизации и неплохо справляется с поиском локального минимума функций с относительно гладким рельефом, поэтому знакомство с методами оптимизации лучше начинать именно с него.
Поиск экстремума ведется в направлении осей координат, т.е. в процессе поиска изменяется только одна координата. Таким образом, многомерная задача сводится к одномерной.
Алгоритм
Первый цикл:
,
,
, ...,
.
- Ищем экстремум функции
. Положим, экстремум функции в точке
.
,
,
, ...,
. Экстремум функции
равен
- ...
,
,
, ...,
.
В результате выполнения n шагов найдена новая точка приближения к экстремуму. Далее проверяем критерий окончания счета: если он выполнен – решение найдено, в противном случае выполняем еще один цикл.
Подготовка
Сверим версии пакетов:
(v1.1) pkg> status
Status `C:UsersUser.juliaenvironmentsv1.1Project.toml`
[336ed68f] CSV v0.4.3
[a93c6f00] DataFrames v0.17.1
[7073ff75] IJulia v1.16.0
[47be7bcc] ORCA v0.2.1
[58dd65bb] Plotly v0.2.0
[f0f68f2c] PlotlyJS v0.12.3
[91a5bcdd] Plots v0.23.0
[ce6b1742] RDatasets v0.6.1
[90137ffa] StaticArrays v0.10.2
[8bb1440f] DelimitedFiles
[10745b16] StatisticsЗададим функцию для отрисовки поверхности либо линий уровня, в которой было бы удобно регулировать границы графика:
using Plots
plotly() # интерактивные графики
function plotter(plot_fun; low, up)
Xs = range(low[1], stop = up[1], length = 80)
Ys = range(low[2], stop = up[2], length = 80)
Zs = [ fun([x y]) for x in Xs, y in Ys ];
plot_fun(Xs, Ys, Zs)
xaxis!( (low[1], up[1]), low[1]:(up[1]-low[1])/5:up[1] ) # линовка осей
yaxis!( (low[2], up[2]), low[2]:(up[2]-low[2])/5:up[2] )
endВ качестве модельной функции выберем эллиптический параболоид
parabol(x) = sum(u->u*u, x)
fun = parabol
plotter(surface, low = [-1 -1], up = [1 1])
Покоординатный спуск
Метод реализуем в функции принимающей название метода одномерной оптимизации, размерность задачи, желаемую погрешность, начальное приближение, и ограничения для отрисовки линий уровня. Всем параметрам зададим значения по-умолчанию.
function ofDescent(odm; ndimes = 2, ε = 1e-4, fit = [.5 .5], low = [-1 -1], up = [1 1])
k = 1 # счетчик для ограничения количества шагов
sumx = 0
sumz = 1
plotter(contour, low = low, up = up) # рисуем контуры рельефа
x = [ fit[1] ] # массив из одного элемента
y = [ fit[2] ] # в них можно пушить координаты
while abs(sumz - sumx) > ε && k<80
fitz = copy(fit)
for i = 1:ndimes
odm(i, fit, ε) # отрабатывает одномерная оптимизация
end
push!(x, fit[1])
push!(y, fit[2])
sumx = sum(abs, fit )
sumz = sum(abs, fitz)
#println("$k $fit")
k += 1
end
# кружочками отрисовать маршрут спуска
scatter!(x', y', legend = false, marker=(10, 0.5, :orange) );# размер, непрозрачность, цвет
p = title!("Age = $(size(x,1)) f(x,y) = $(fun(fit))")
endДалее опробуем различные методы одномерной оптимизации
Метод Ньютона
Идея метода проста как и реализация
# производная
dfun = (x, i) -> i == 1 ? 2x[1] + x[2]*x[2] : 2x[2] + x[1]*x[1]
function newton2(i, fit, ϵ)
k = 1
oldfit = Inf
while ( abs(fit[i] - oldfit) > ϵ && k<50 )
oldfit = fit[i]
tryfit = fun(fit) / dfun(fit, i)
fit[i] -= tryfit
println(" $k $fit")
k+=1
end
end
ofDescent(newton2, fit = [9.1 9.1], low = [-4 -4], up = [13 13])
Ньютон довольно требователен к начальному приближению, а без ограничения по шагам вполне может ускакать в неведанные дали. Расчет производной желателен, но можно обойтись и малым варьированием. Модифицируем нашу функцию:
function newton(i, fit, ϵ)
k = 1
oldfit = Inf
x = []
y = []
push!(x, fit[1])
push!(y, fit[2])
while ( abs(oldfit - fit[i]) > ϵ && k<50 )
fx = fun(fit)
oldfit = fit[i]
fit[i] += 0.01
dfx = fun(fit)
fit[i] -= 0.01
tryfit = fx*0.01 / (dfx-fx)
# обрубаем при заскоке значения функции на порядок
if( abs(tryfit) > abs(fit[i])*10 )
push!(x, fit[1])
push!(y, fit[2])
break
end
fit[i] -= tryfit
#println(" $k $fit")
push!(x, fit[1])
push!(y, fit[2])
k+=1
end
# траекторию Одном-й оптим-ии рисуем квадратиками
plot!(x, y, w = 3, legend = false, marker = :rect )
end
ofDescent(newton, fit = [9.1 9.1], low = [-4 -4], up = [13 13])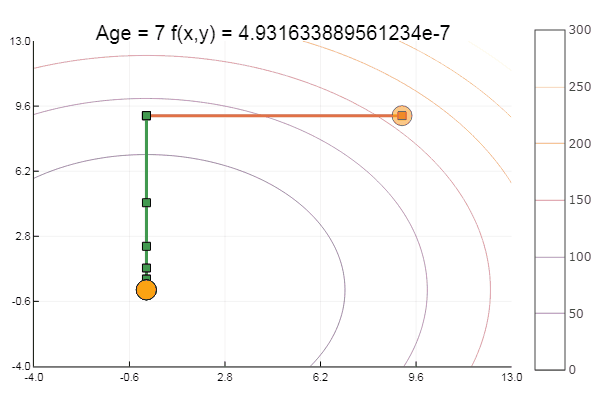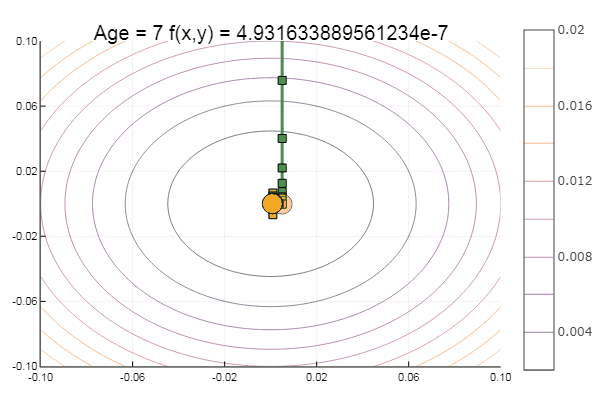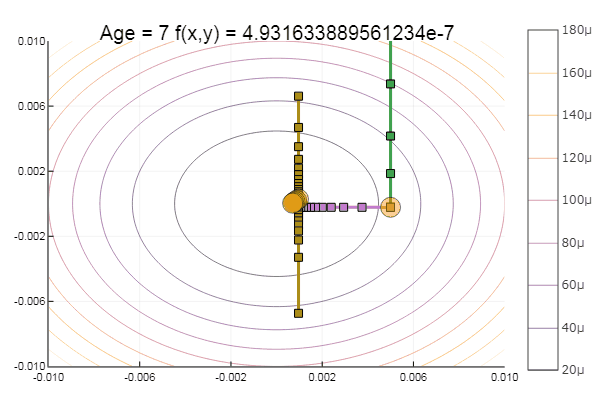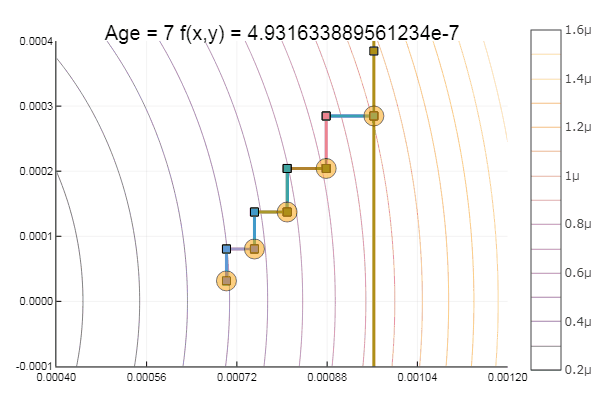
Обратная параболическая интерполяция
Метод не требующий знания производной и имеющий неплохую сходимость
function ipi(i, fit, ϵ) # inverse parabolic interpolation
n = 0
xn2 = copy(fit)
xn1 = copy(fit)
xn = copy(fit)
xnp = zeros( length(fit) )
xy = copy(fit)
xn2[i] = fit[i] - 0.15
xn[i] = fit[i] + 0.15
fn2 = fun(xn2)
fn1 = fun(xn1)
while abs(xn[i] - xn1[i]) > ϵ && n<80
fn = fun(xn)
a = fn1*fn / ( (fn2-fn1)*(fn2-fn ) )
b = fn2*fn / ( (fn1-fn2)*(fn1-fn ) )
c = fn2*fn1 / ( (fn -fn2)*(fn -fn1) )
xnp[i] = a*xn2[i] + b*xn1[i] + c*xn[i]
xn2[i] = xn1[i]
xn1[i] = xn[i]
xn[i] = xnp[i]
fn2 = fn1
fn1 = fn
n += 1
println(" $n $xn $xn1")
xy = [xy; xn]
end
fit[i] = xnp[i]
plot!(xy[:,1], xy[:,2], w = 3, legend = false, marker = :rect )
end
ofDescent(ipi, fit = [0.1 0.1], low = [-.1 -.1], up = [.4 .4])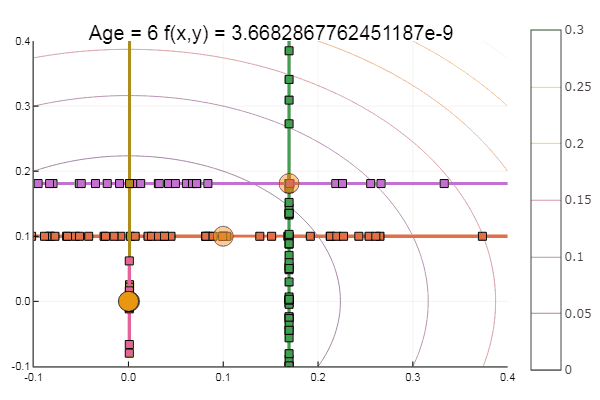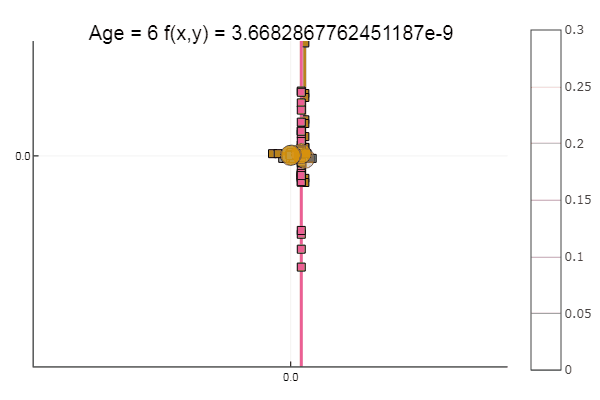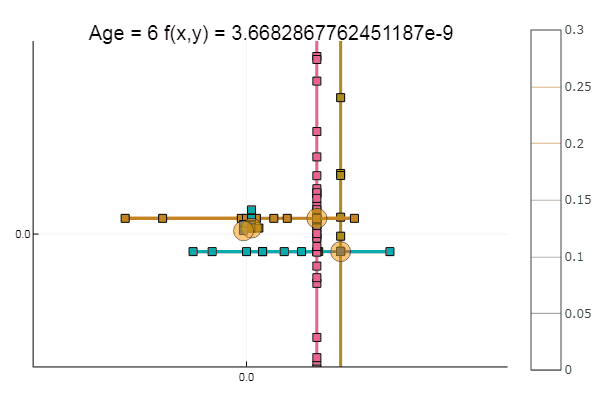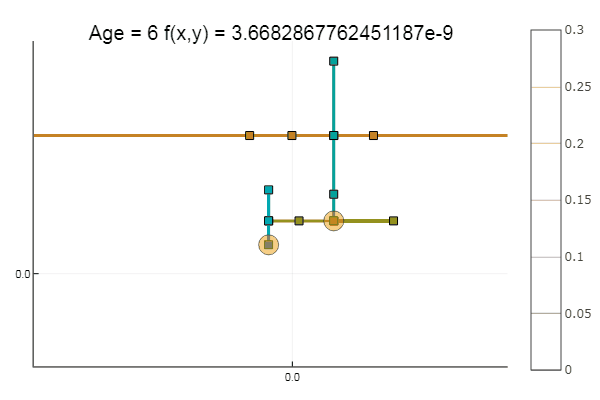
Если взять начальное приближение похуже, метод начнет требовать немеренное количество шагов на каждую эпоху покоординатного спуска. В этом плане у него выигрывает братец
Последовательная параболическая интерполяция
Тоже требует три начальных точки, но на многих тестовых функциях показывает более удовлетворительные результаты
function spi(i, fit, ϵ) # sequential parabolic interpolation
n = 0
xn2 = copy(fit)
xn1 = copy(fit)
xn = copy(fit)
xnp = zeros( length(fit) )
xy = copy(fit)
xn2[i] = fit[i] - 0.01
xn[i] = fit[i] + 0.01
fn2 = fun(xn2)
fn1 = fun(xn1)
while abs(xn[i] - xn1[i]) > ϵ && n<200
fn = fun(xn)
v0 = xn1[i] - xn2[i]
v1 = xn[i] - xn2[i]
v2 = xn[i] - xn1[i]
s0 = xn1[i]*xn1[i] - xn2[i]*xn2[i]
s1 = xn[i] *xn[i] - xn2[i]*xn2[i]
s2 = xn[i] *xn[i] - xn1[i]*xn1[i]
xnp[i] = 0.5(fn2*s2 - fn1*s1 + fn*s0) / (fn2*v2 - fn1*v1 + fn*v0)
xn2[i] = xn1[i]
xn1[i] = xn[i]
xn[i] = xnp[i]
fn2 = fn1
fn1 = fn
n += 1
println(" $n $xn $xn1")
xy = [xy; xn]
end
fit[i] = xnp[i]
plot!(xy[:,1], xy[:,2], w = 3, legend = false, marker = :rect )
end
ofDescent(spi, fit = [16.1 16.1], low = [-.1 -.1], up = [.4 .4])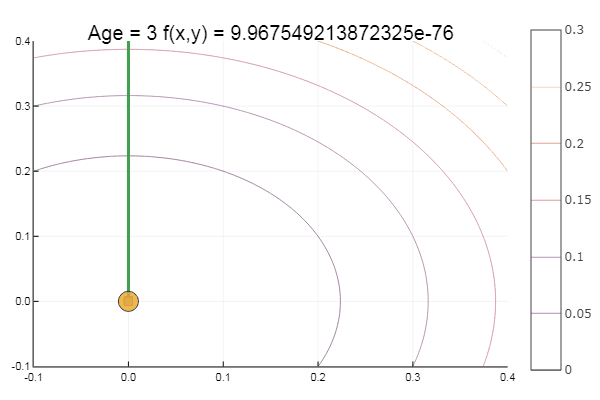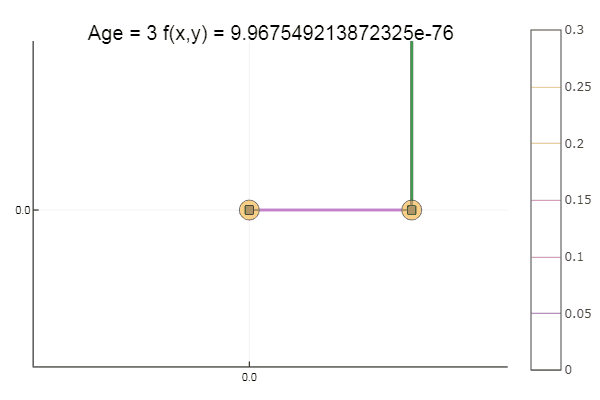
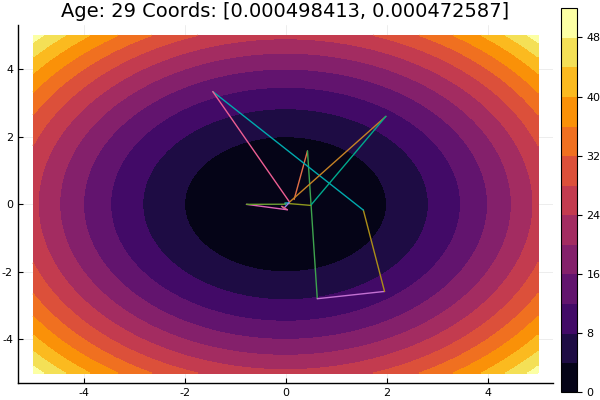
Выйдя из весьма дрянной стартовой точки дошло за три шага! Хорош… Но у всех методов есть недостаток — они сходятся к локальному минимуму. Возьмём теперь для исследований функцию Экли
ekly(x) = -20exp(-0.2sqrt(0.5(x[1]*x[1]+x[2]*x[2]))) - exp(0.5(cospi(2x[1])+cospi(2x[2]))) + 20 + ℯ
# f(0,0) = 0, x_i ∈ [-5,5]
fun = ekly
plotter(surface, low = [-5 -5], up = [5 5])

ofDescent(spi, fit = [1.4 1.4], low = [-.1 -.1], up = [2.4 2.4])
Метод золотого сечения
Теория. Хоть реализация сложна, метод порой показывает себя хорошо перепрыгивая локальные минимумы
function interval(i, fit, st)
d = 0.
ab = zeros(2)
fitc = copy(fit)
ab[1] = fitc[i]
Fa = fun(fitc)
fitc[i] -= st
Fdx = fun(fitc)
fitc[i] += st
if Fdx < Fa
st = -st
end
fitc[i] += st
ab[2] = fitc[i]
Fb = fun(fitc)
while Fb < Fa
d = ab[1]
ab[1] = ab[2]
Fa = Fb
fitc[i] += st
ab[2] = fitc[i]
Fb = fun(fitc)
# println("----", Fb, " ", Fa)
end
if st < 0
c = ab[2]
ab[2] = d
d = c
end
ab[1] = d
ab
end
function goldsection(i, fit, ϵ)
ϕ = Base.MathConstants.golden
ab = interval(i, fit, 0.01)
α = ϕ*ab[1] + (1-ϕ)*ab[2]
β = ϕ*ab[2] + (1-ϕ)*ab[1]
fit[i] = α
Fa = fun(fit)
fit[i] = β
Fb = fun(fit)
while abs(ab[2] - ab[1]) > ϕ
if Fa < Fb
ab[2] = β
β = α
Fb = Fa
α = ϕ*ab[1] + (1-ϕ)*ab[2]
fit[i] = α
Fa = fun(fit)
else
ab[1] = α
α = β
Fa = Fb
β = ϕ*ab[2] + (1-ϕ)*ab[1]
fit[i] = β
Fb = fun(fit)
end
println(">>>", i, ab)
plot!(ab, w = 1, legend = false, marker = :rect )
end
fit[i] = 0.5(ab[1] + ab[2])
end
ofDescent(goldsection, fit = [1.4 1.4], low = [-.1 -.1], up = [1. 1.])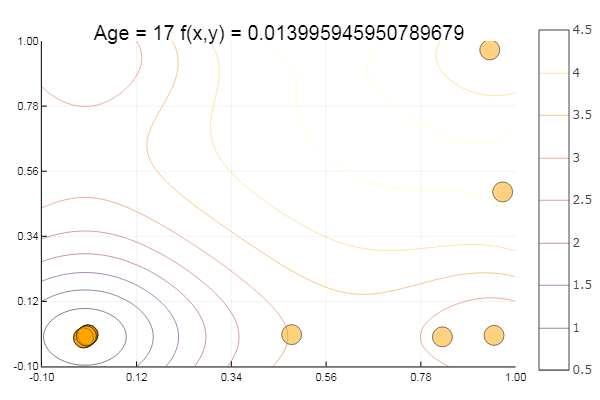
На этом с покоординатным спуском всё. Алгоритмы представленных методов довольно просты, так что имплементировать их на предпочитаемом языке не составит труда. В дальнейшем можно рассмотреть встроенные средства языка Julia, но пока хочется всё, так сказать, пощупать руками, рассмотреть методы посложней и поэффективней, затем можно перейти к глобальной оптимизации, попутно сравнивая с реализацией на другом языке.
Литература
- Зайцев В. В. Численные методы для физиков. Нелинейные уравнения и оптимизация: учебное пособие. – Самара, 2005г. – 86с.
- Иванов А. В. Компьютерные методы оптимизации оптических систем. Учебное пособие. –СПб: СПбГУ ИТМО, 2010 – 114с.
- Попова Т. М. Методы многомерной оптимизации: методические указания и задания к выполнению лабораторных работ по дисциплине «Методы оптимизации» для студентов направления «Прикладная математика»/ сост. Т. М. Попова. – Хабаровск: Изд-во Тихоокеан. гос. ун-та, 2012. – 44 с.
Автор: Yermack




![Julia и метод покоординатного спуска - 25 $f(x,y)=-20exp left[-0.2{sqrt {0.5left(x^{2}+y^{2}right)}}right]-exp left[0.5left(cos 2pi x+cos 2pi yright)right]+e+20$](https://www.pvsm.ru/images/2019/02/12/Julia-i-metod-pokoordinatnogo-spuska-25.svg)