Сдал сопромат — можно жениться!
Введение
Метод конечных элементов (МКЭ или FEM, у них за рубежом) прочно вошел в практику инженерных расчетов при проектировании сложных систем. В значительной степени это касается прочностных расчетов механики. Применения этого метода, реализуемого соответствующим программным обеспечением существенно сокращает цикл разработки конечного устройства, позволяя исключить массу экспериментальных проверок, необходимых при использования классических расчетов на основе методов сопромата и строительной механики. На текущий момент разработана масса прикладного ПО, реализующего МКЭ. Во главе угла стоит мощный ANSYS, по бокам от него и в почетном удалении — CAD-системы со встроенным FEM-модулем (SolidWorks, Siemens NX, Creo Parametric, Компас 3D).
CalculiX силен, но труден и непонятен. Исправим это?
Естественно, МКЭ проник и в сферу образования — чтобы использовать его в реальных задачах, нужна подготовка соответствующих специалистов. В столицах, в крупных технических вузах обстановка в этой области более-менее нормальная, да и у нас в регионе тот же ANSYS применяется, например, на кафедре теории упругости ЮФУ. Но по периферии, в узко специализированных и не богатых университетах ситуация плачевна. И всё просто — ANSYS стоит порядка 2 млн. рублей за одно рабочее место, а место требуется не одно. К сожалению не все вузы могут позволить себе выложить 30-40 миллионов на организацию компьютерного класса для обучения применению МКЭ.
Одной из альтернатив может служить применение в учебном процессе свободного ПО. К счастью таковое ПО имеется. Однако, русскоязычных материалов по его использованию практически не существует. Исправляя эту ситуацию, данную статью я собираюсь посвятить в введению в CalculiX — открытый, свободный программный пакет, предназначенный для решения линейных и нелинейных трёхмерных задач механики твёрдого деформируемого тела и механики жидкости и газа с помощью метода конечных элементов.
1. Что такое CalculiX и где его взять. Установка в Windows
Пакет CalculiX представляет собой набор консольных утилит, включающих препроцессор для подготовки исходных данных, МКЭ-решатель и постпроцессор для обработки результатов. CalculiX используется как самостоятельно, так и в составе других продуктов, среди которых особенно выделяется набирающий обороты FreeCAD. Другой вопрос, что CalculiX пока что мало известен у нас в стране, о чем прямо говорится единственной статье о нем на этом ресурсе.
Я специально буду излагать весть нижеследующий материал применительно к работе в ОС Windows, как самой распространенной и применяемой в том числе и учебных заведениях. При этом использование многих свободных программ в ней представляет собой откровенную боль.
Если брать пакет для Windows с официального сайта CalculiX, то становится совершенно непонятно, что с ним делать дальше. В совокупности с англоязычной документацией это, для многих ставит крест на данном продукте, а потом выливается в ядовитые комментарии по поводу невозможности его использования. И отчасти это справедливо — порог вхождения действительно высок. Но всё же мы попытаемся.
Существует ряд неофициальных относительно дружественных к новичку сборок сего чуда под Windows, среди них bConverged CalculiX for Windows. Качаем дистрибутив отсюда, распаковываем, и устанавливаем его стандартным методом «далее, далее...». Установка, таким образом, не представляет собой особого таинства и вполне доступна неискушенному пользователю. В качестве основной рабочей среды в данном пакете используется текстовый редактор SciTE, в который интегрированы вызовы компонентов CalculiX, а также представляется возможность интерактивного ввода команд и выглядит оно примерно так (кликабельно)
2. Задача об изгибе балки и её аналитическое решение методами сопромата
Возьмем простую студенческую задачку — изгиб стальной балки, один конец которой защемлен, а к другому прикладывается вертикальная сила F.
Параметры задачи таковы: F = 10 кН; l = 1 м — длина балки; h = 0,1 м и b = 0,05 м — размеры поперечного сечения. Для простоты не будем учитывать собственный вес балки, так как он, при массе балки 39 кг существенно меньше чем приложенная нагрузка. Найдем максимальное нормальное напряжение в сечении балки а так же вычислим прогиб балки в следствии деформации изгиба.
Любой студент, не прогуливавший сопромат с легкостью решит такую задачку. Дабы не смущать благородных донов, все подробности решения я заверну в спойлер
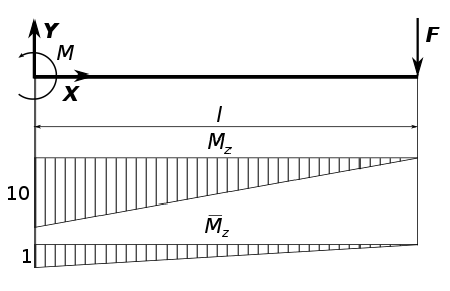
Без лишних трудов находим реакции связей из уравнений статики
Откуда 
и 
. Эпюра изгибающих моментов и единичная эпюра изгибающих моментов (необходима для применения интеграла Мора) строятся тривиально и показаны на рисунке. Максимальное нормальное напряжение пи изгибе балки равно
где 
м — максимальное расстояние от крайних точек сечения до продольной оси балки; 
— геометрический момент инерции относительно оси изгиба, равный
Путем несложных вычислений для конкретных данных получаем, что максимальное нормальное напряжение будет 
МПа
Максимальный прогиб балки при изгибе вычислим, используя интеграл Мора
где E = 200 ГПа — модуль Юнга для стали. Вычисления для конкретных значений дают 
, м.
Для тех кому лень смотреть под спойлер, зразу приведу ответ задачи: максимальное нормальное напряжение в сечении балки 
МПа, а максимальный прогиб составляет 3,97 миллиметра. Эти цифры приводятся для последующего сравнения с тем, что даст нам процедура решения этой задачки в CalculiX.
3. Подготовка геометрии и расчетной сетки
Прежде всего необходимо ввести в CalculiX геометрические данные о рассматриваемой детали. Да, тут возможен экспорт геометрии из CAD-ов, как это делается в том же ANSYS, но мы поёдем путем мучений и введем геометрию вручную. Открываем редактор SciTE из комплекта bConverged и набираем там следующий текст
pnt p1 0 0 0
pnt p2 0.25 0 0
pnt p3 0.5 0 0
pnt p4 0.75 0 0
pnt p5 1.0 0 0
Сохраняем файл с именем beam.fbd и жмем F10 для запуска препроцессинга. Мы увидим примерно следующее
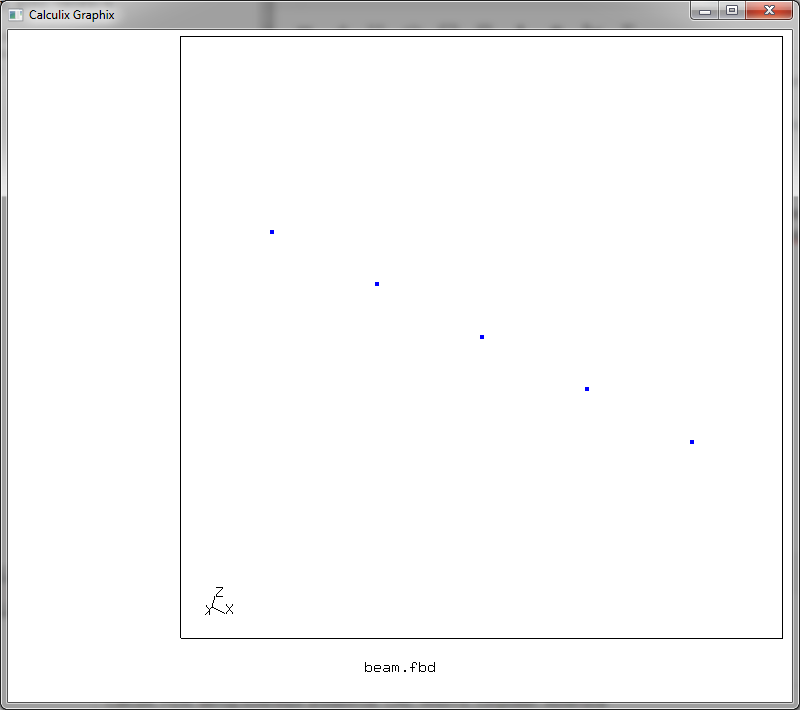
Команда pnt создает точку в пространстве с заданными координатами и синтаксис её таков
pnt [имя точки] [x] [y] [z]
Теперь соединим эти точки линиями, добавив в файл следующий текст
line l1 p1 p2 25
line l2 p2 p3 25
line l3 p3 p4 25
line l4 p4 p5 25
получив после нажатия F10 следующую картинку
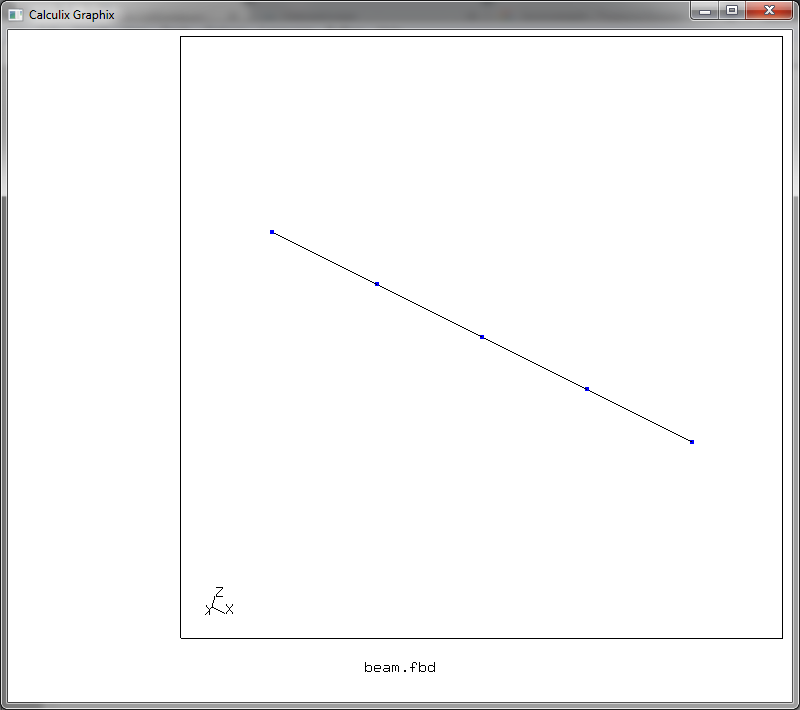
Команда
line [имя линии] [точка 1] [точка 2] [число сегментов линии]
создает линию, соединяющую указанные в ней точки, добавляя промежуточные точки, разбивающие линию на указанное число сегментов (в нашем случае 25 для каждой линии). Это пригодится потом для генерации сетки. Теперь делаем финт ушами
seta lines l l1 l2 l3 l4
swep lines sweeplines tra 0 0 0.1 10
Первая команда
seta [имя набора] [объект 1] ... [объект N]
объединяет несколько объектов в набор с заданным именем. По сути это аналог группировки объектов. Следующая команда
swep [имя объекта или набора объектов] [имя нового набора объектов] [вид перемещения] [вектор, задающий перемещение] [параметр]
выполняет перемещение выбранного набора объектов с образованием нового набора. Перемещаемые объекты копируются. При этом движение точек образует линии, движение линий — поверхности, движение поверхностей — сплошные объемы. В нашем случае мы смещаем набор линий lines на вдоль оси Z на 0.1 метра, при этом, образующиеся линии делятся на 10 сегментов. Жмем F10… э, а что это?
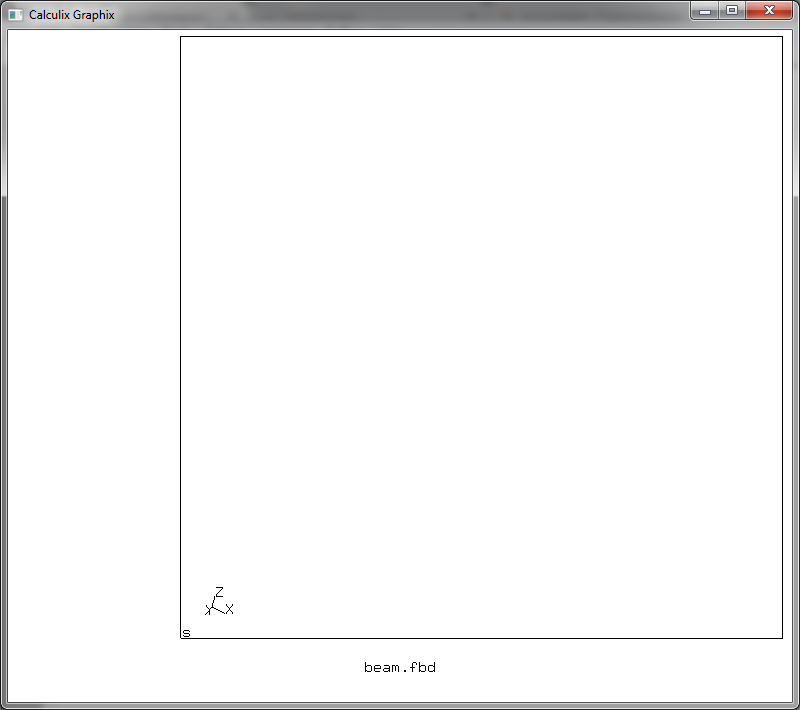
Гхм, пустой экран… Исправляется это легко, достаточно добавить в конец скрипта строчки
plot pa all
plus la all
Эти команды указывают рисовать все точки (pa) и добавить к отображению все линии (la), после чего мы получаем такой результат
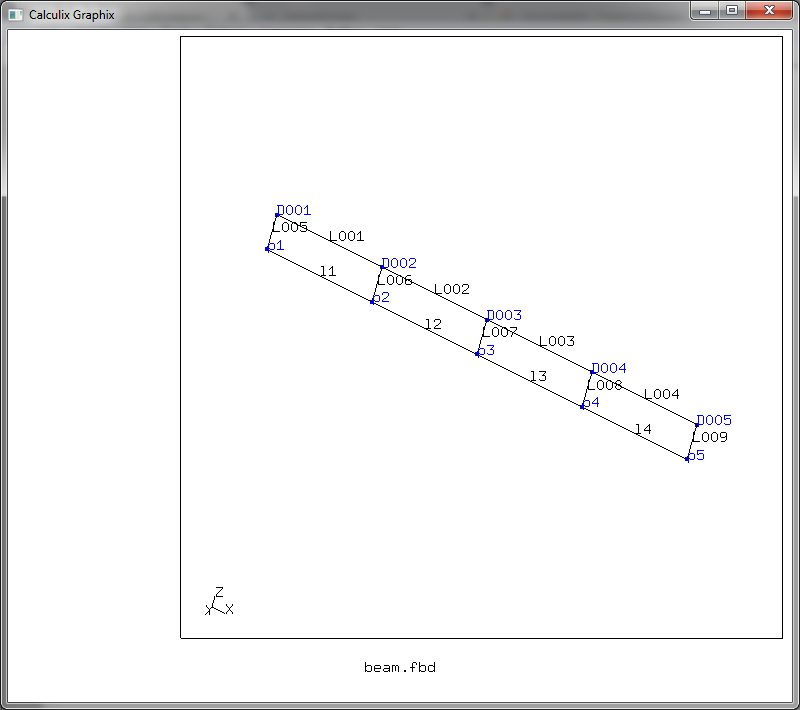
Теперь создадим поверхности, на базе созданного нами набора линий
seta surfaces s A001 A002 A003 A004
добавив в самый конец скрипта отображение этих поверхностей
plus sa all
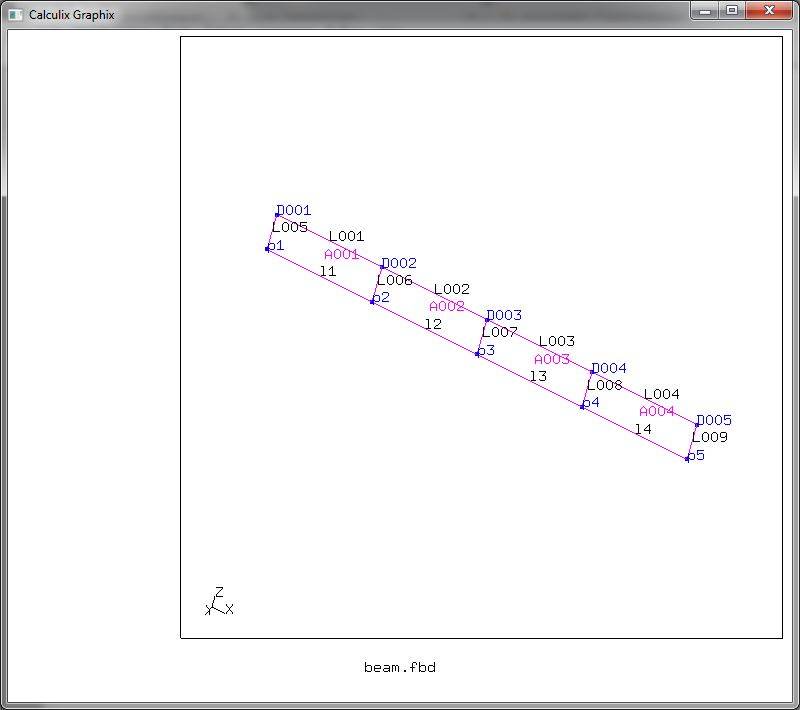
Теперь выполним ещё один сдвиг, теперь уже вдоль оси Y на 0,05 метров, развивая все образующиеся при смещении линии на 5 сегментов.
swep surfaces swepsurface tra 0.0 0.05 0.0 5
Получим что-то в духе
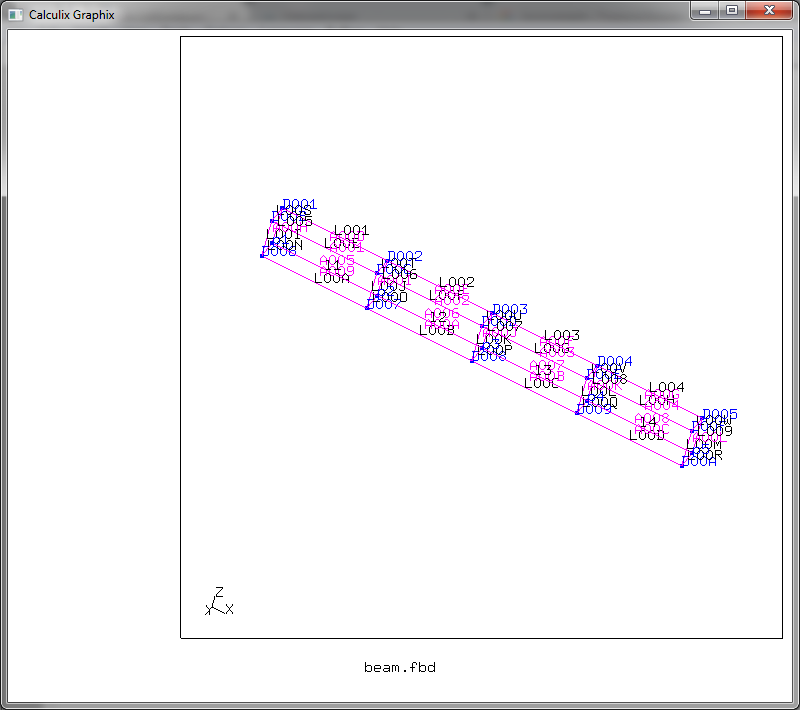
Полученное изображение можно повертеть, зажав левую кнопку мыши, и убрав отображение точек и линий, мы увидим нечто вразумительное
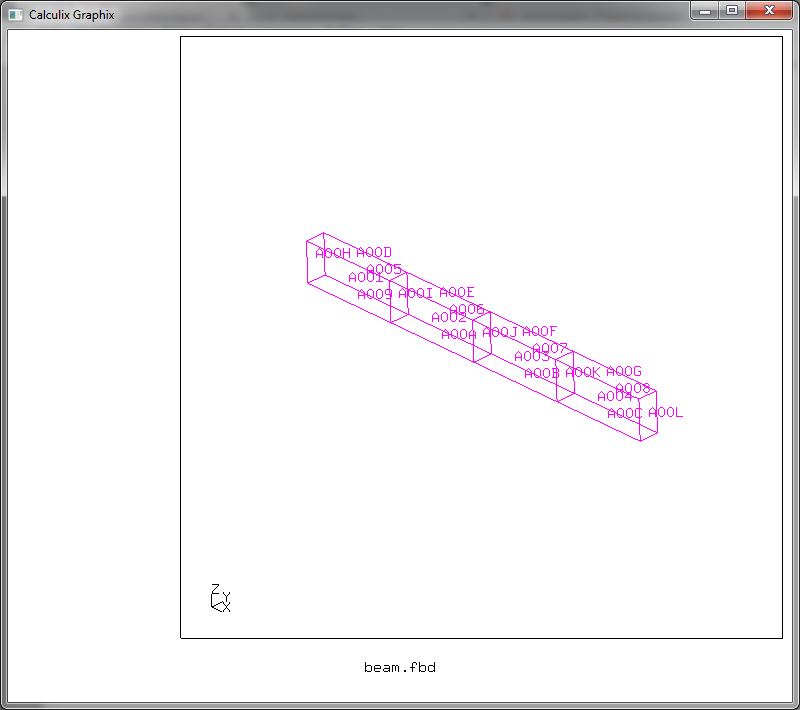
Дааа… CalculiX далек от привычных массовому пользователю визуальных концепций, но тем не менее мы построили геометрию нашей балки.
Геометрия, геометрией, но для генерации сетки сделаем следующий ход — уберем все команды plot и plus и обернем код генерации геометрии в команды seto и setc, вот так
seto beam
pnt p1 0 0 0
pnt p2 0.25 0 0
pnt p3 0.5 0 0
pnt p4 0.75 0 0
pnt p5 1.0 0 0
line l1 p1 p2 25
line l2 p2 p3 25
line l3 p3 p4 25
line l4 p4 p5 25
seta lines l l1 l2 l3 l4
swep lines sweeplines tra 0 0 0.1 10
seta surfaces s A001 A002 A003 A004
swep surfaces swepsurface tra 0 0.05 0 5
setc beam
Эта пара команд объединяет всю созданную геометрию в некий блок геометрии с именем beam. Теперь эту геометрическую группу можно пропустить через генерацию сетки, указав после всего вышеупомянутого кода команды
elty beam he8
mesh beam
— генерирует сетку, состоящую из параллелепипедов (he8) на основе геометрии с именем beam. Теперь выводим сгенерированную сетку в файл
send beam abq
— вывод сетки в файл с именем beam.msh в формате FEM-пакета ABAQUS (есть и такой проприетарный пакет МКЭ-вычислений и CalculiX его формат понимает)
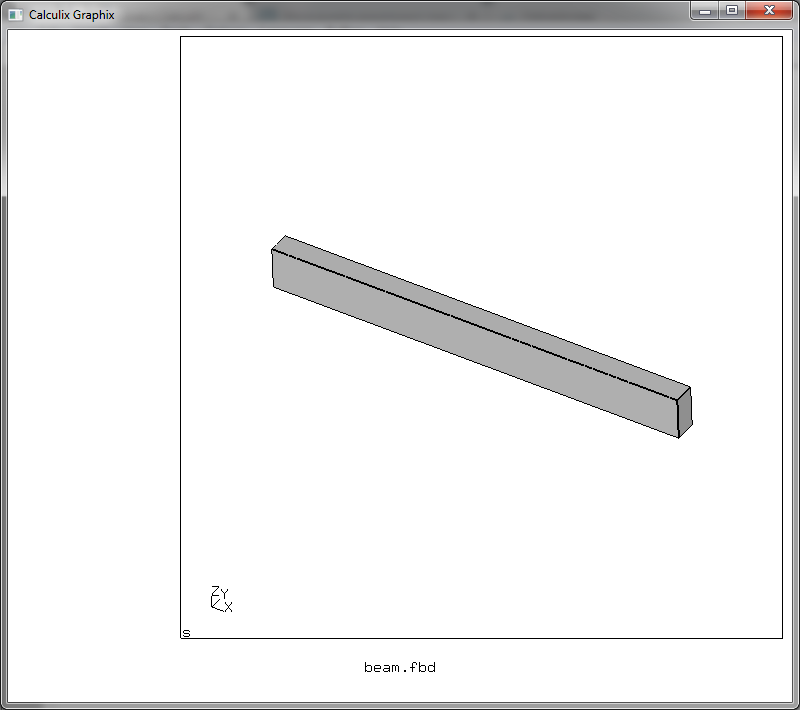
Таким образом сетка сгенерирована, можно глянуть в файл beam.msh и увидеть там что-то подобное этому
*NODE, NSET=Nbeam
1,0.000000000000e+000,0.000000000000e+000,1.000000000000e-001
2,0.000000000000e+000,0.000000000000e+000,9.000000000000e-002
3,0.000000000000e+000,1.000000000000e-002,9.000000000000e-002
4,0.000000000000e+000,1.000000000000e-002,1.000000000000e-001
5,1.000000000000e-002,0.000000000000e+000,1.000000000000e-001
6,1.000000000000e-002,0.000000000000e+000,9.000000000000e-002
7,1.000000000000e-002,1.000000000000e-002,9.000000000000e-002
8,1.000000000000e-002,1.000000000000e-002,1.000000000000e-001
9,0.000000000000e+000,2.000000000000e-002,9.000000000000e-002
10,0.000000000000e+000,2.000000000000e-002,1.000000000000e-001
11,1.000000000000e-002,2.000000000000e-002,9.000000000000e-002
.
.
.
.
*ELEMENT, TYPE=C3D8, ELSET=Ebeam
1, 1, 2, 3, 4, 5, 6, 7, 8
2, 4, 3, 9, 10, 8, 7, 11, 12
3, 10, 9, 13, 14, 12, 11, 15, 16
4, 14, 13, 17, 18, 16, 15, 19, 20
5, 18, 17, 21, 22, 20, 19, 23, 24
6, 5, 6, 7, 8, 25, 26, 27, 28
7, 8, 7, 11, 12, 28, 27, 29, 30
8, 12, 11, 15, 16, 30, 29, 31, 32
9, 16, 15, 19, 20, 32, 31, 33, 34
По-видимому это список вершин элементов сетки с их координатами, за которым следует список граней. Чтобы всё это дело выглядело более красиво, воспользуемся интерактивным режимом CalculiX. Для этого, оставляя активным графическое окно, вводим последовательно следующие команды
plot f beam
— отображаем все грани геометрии
view edge off
— отключаем отображение ребер
view elem
— включаем отображение элементов сетки. Ввод каждой команды завершаем нажатием Enter, введенные команды отображаются в окне SciTE справа внизу, вот так
Да, нельзя назвать это суперудобным, но тем не менее мы получим изображение сгенерированной сетки.
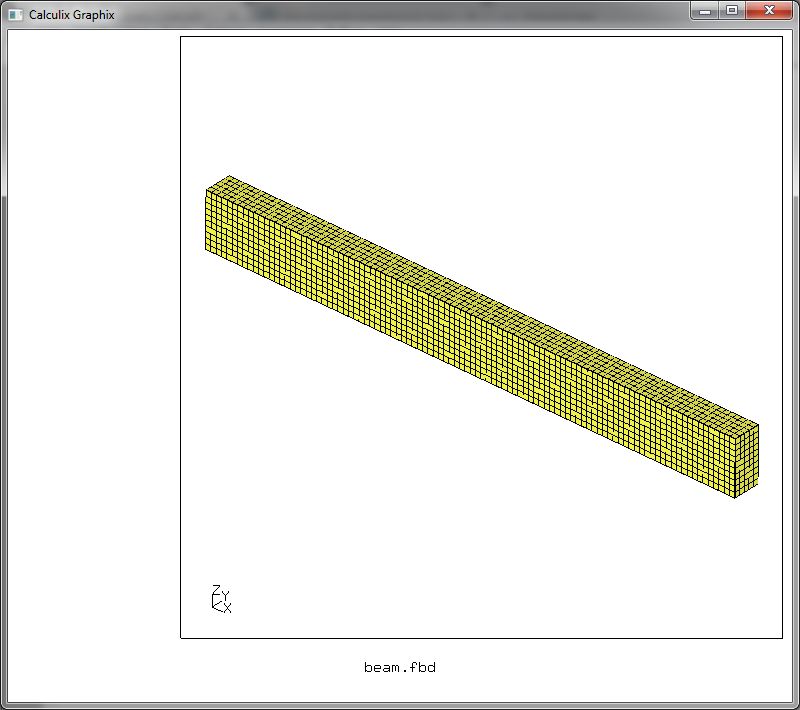
Замечу, что все промежуточные точки, что были созданы при создании геометрии стали узлами сетки. Таким образом мы получили гексагональную сетку размером 100 х 10 х 5 узлов, с размером ребра элемента в 10 мм. Созданный нами файл beam.fbd описывает геометрию задачи и процесс создания сетки.
seto beam
pnt p1 0 0 0
pnt p2 0.25 0 0
pnt p3 0.5 0 0
pnt p4 0.75 0 0
pnt p5 1.0 0 0
line l1 p1 p2 25
line l2 p2 p3 25
line l3 p3 p4 25
line l4 p4 p5 25
seta lines l l1 l2 l3 l4
swep lines sweeplines tra 0 0 0.1 10
seta surfaces s A001 A002 A003 A004
swep surfaces swepsurface tra 0 0.05 0 5
setc beam
elty beam he8
mesh beam
send beam abq
4. Задание ограничений
Важным этапом применения МКЭ является задание ограничений перемещения точек конструкции, то есть учет наложенных на неё связей. В нашем случае один из концов балки защемлен, а значить можно считать, что один из её торцов полностью неподвижен. Нам нужно сообщить решателю, какие узлы КЭ-сетки являются неподвижными. Жмем F10 при открытом файле beam.fbd, дожидаемся появления окна с изображением балки
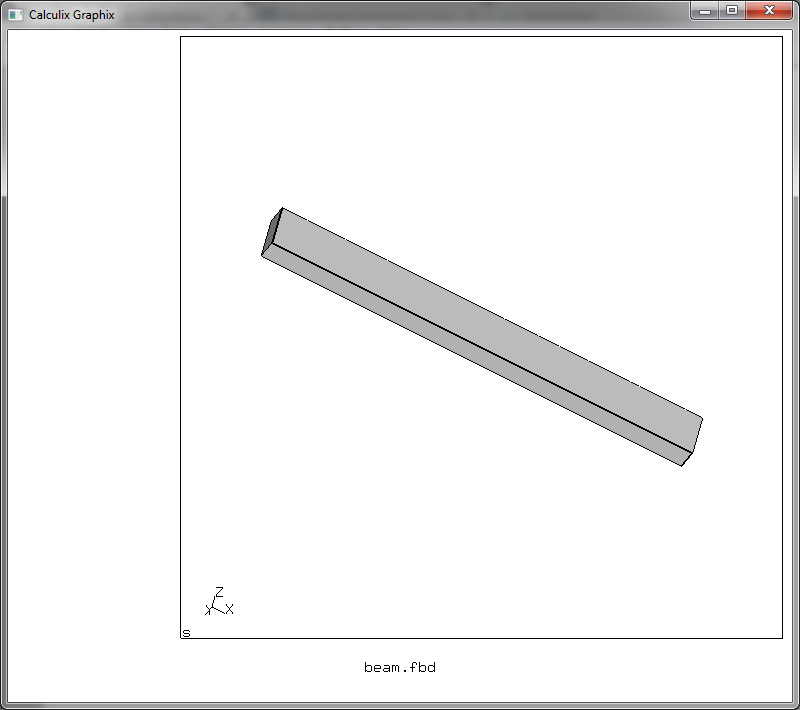
В интерактивном режиме вводим команды
rot -y
plot n beam
Первая команда разворачивает модель так, чтобы ось Y смотрела от нас, вторая — включает отрисовку узлов (n) КЭ-сетки. Двигая модель (зажав правую кнопку мыши) и масштабируя изображение (зажав колесо мыши) добиваемся такой картинки
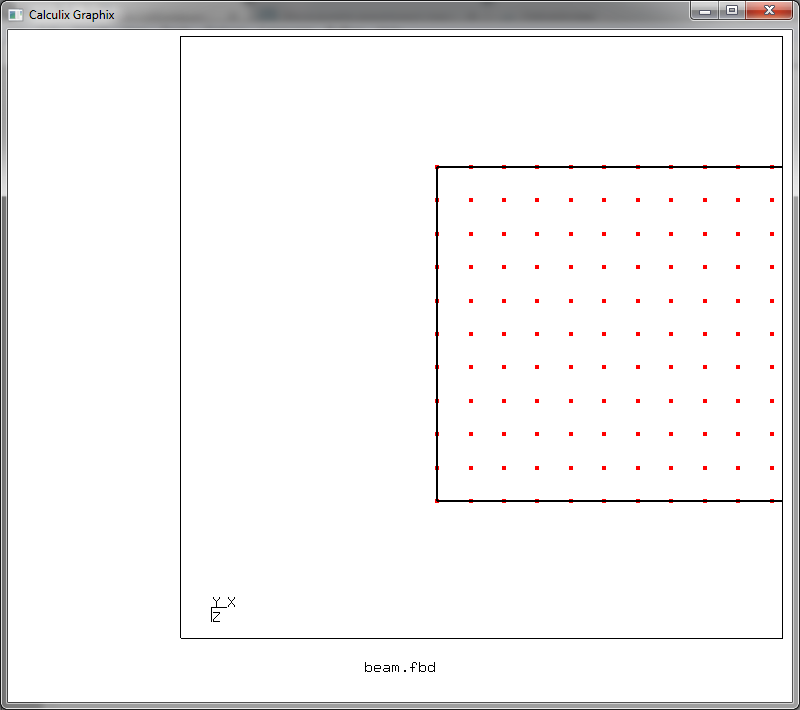
Теперь надо выбрать все узлы, которые мы хотим определить как неподвижные. Для этого опять используем интерактивный режим ввода данных. Набираем команду
qadd fixed
что начинает создание набора узлов с именем fixed. Курсор на графическом окне переключается в режим выбора элементов — отображается в виде стрелки с маленьким квадратиком. Ставим курсор так
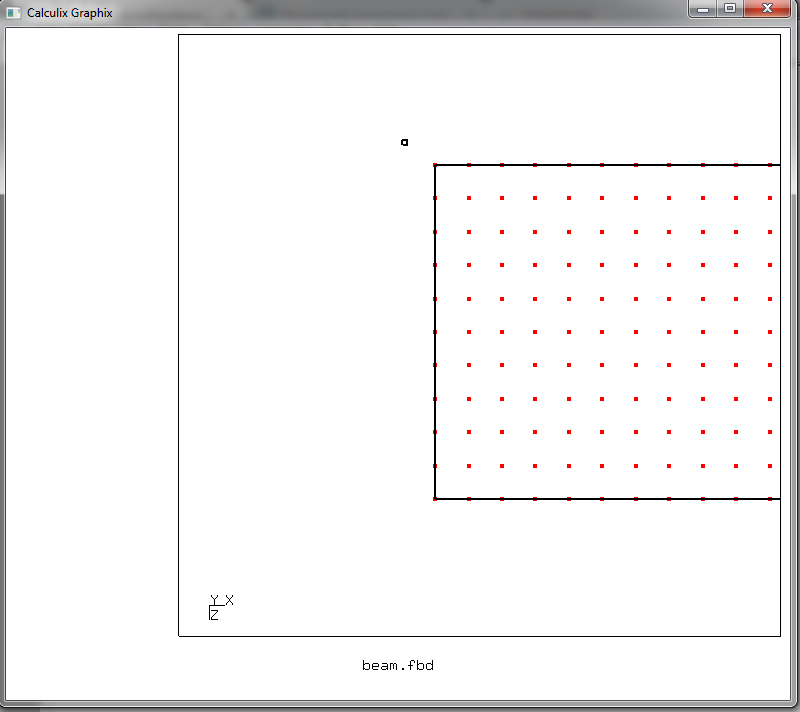
и жмем клавишу r. А затем ставим курсор так
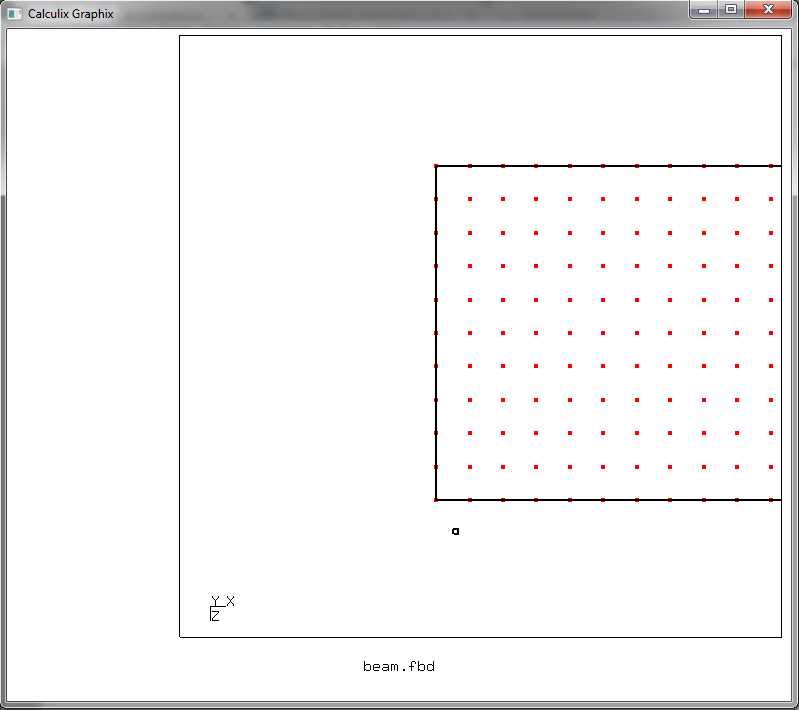
и снова жмем r. Таким образом, мы сформировали область выбора прямоугольной формы, диагональ которой задается отмеченными нажатием r положениями курсора. Выделяем этим прямоугольником нужные нам узлы, лежащие на торце балки
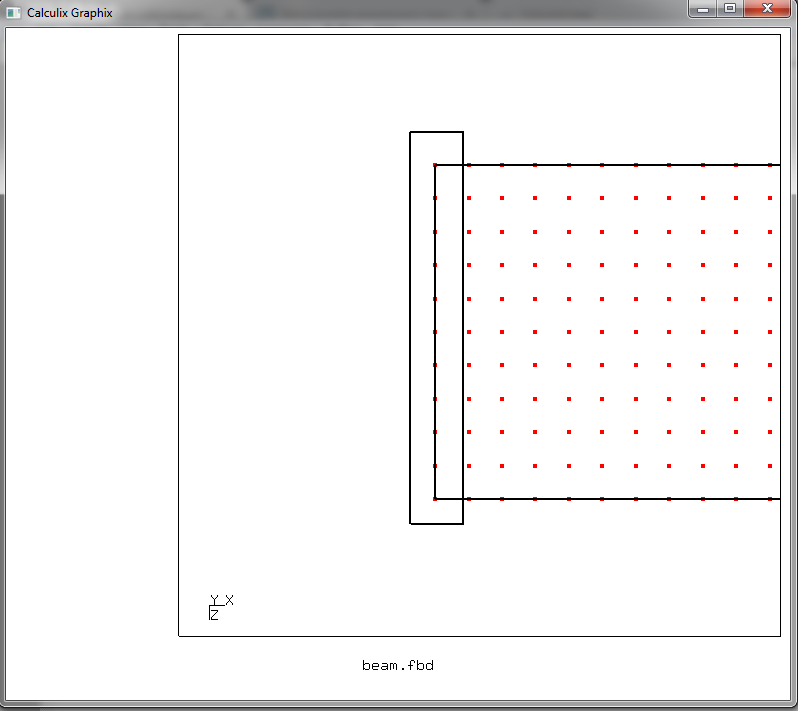
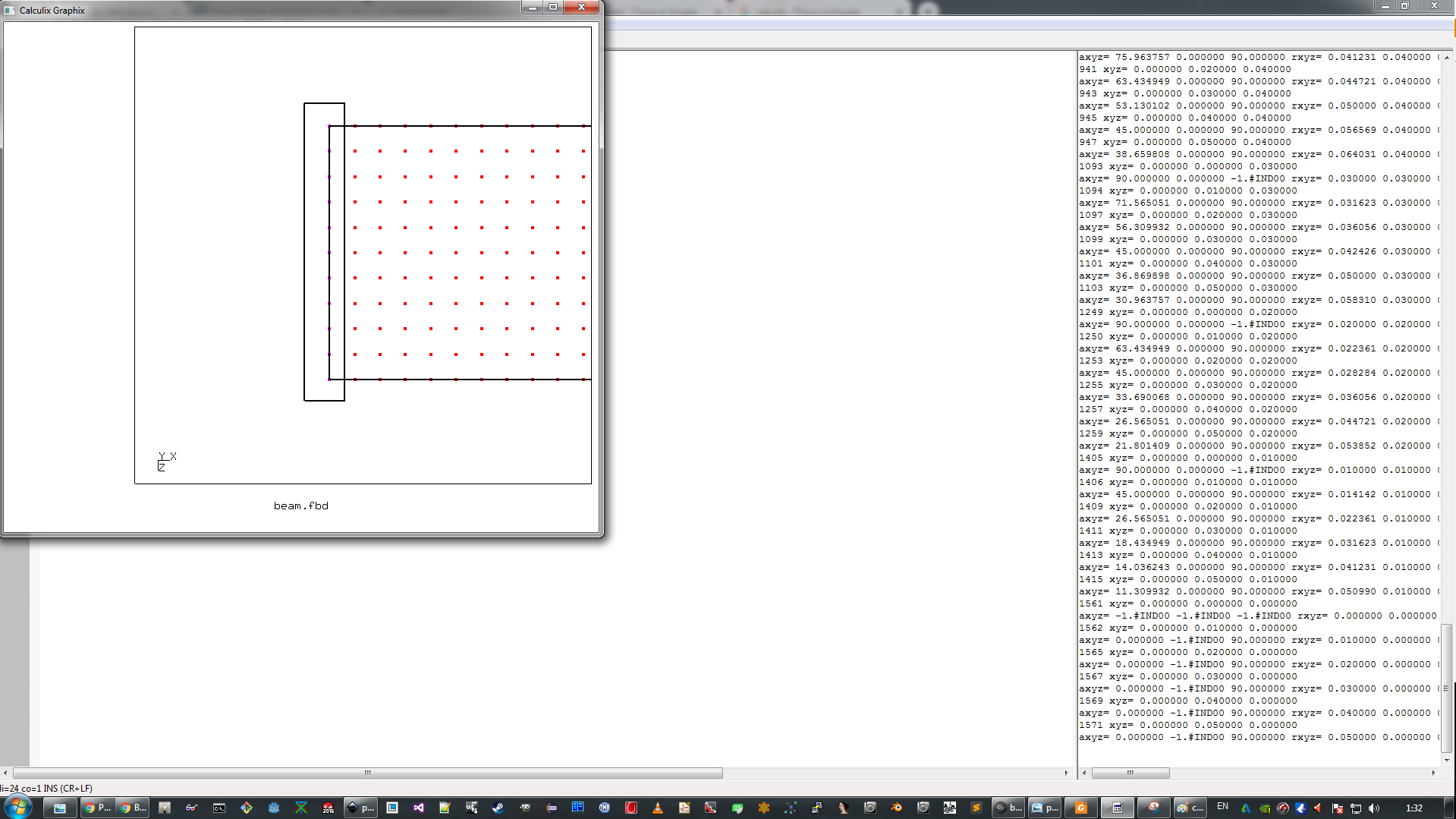
жмем a а затем жмем n, выделяя отмеченные узлы. В консольном окне появится портянка со списком выделенных узлов (картинка кликабельна)
Вводим q для выхода из режима выбора и команду
plus n fixed g
для отображения узлов группы fixed зеленым цветом (g). Теперь мы можем увидеть, какие узлы у нас будут входить в условие закрепления
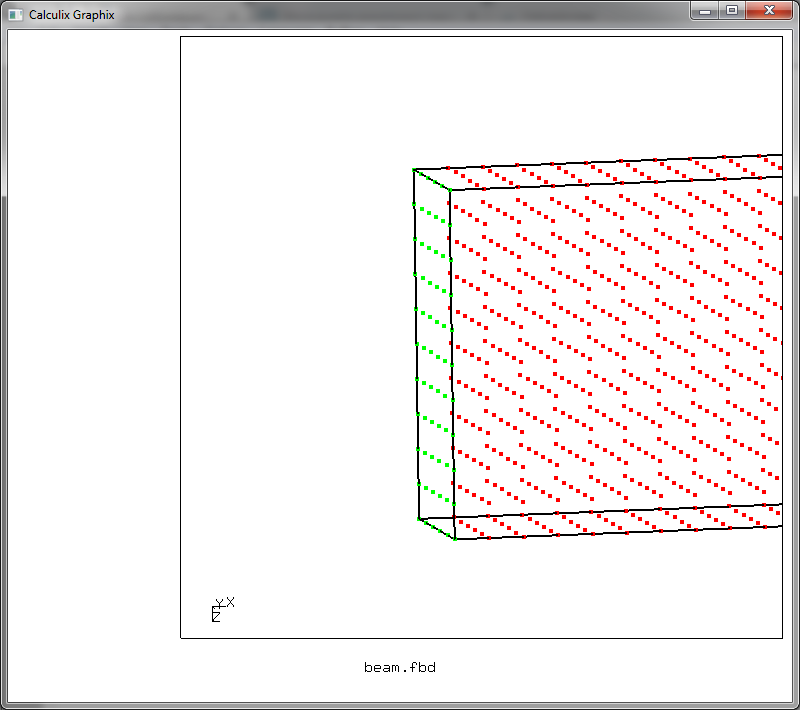
Теперь мы должны выгрузить эти узлы в качестве файла ограничений, подаваемого в дальнейшем на вход решателя. Для этого набираем команду
send fixed abq spc 123
— выгрузить группу узлов fixed в виде файла ограничений в формате ABAQUS (abq), ограничив перемещение всех узлов группы по всем трем степеням свободы (1 — ось X, 2 — ось Y, 3 — ось Z). В итоге образуется файл fixed_123.bou, следующего содержания
** BOUNDARY based on fixed
1, 1, ,
2, 1, ,
3, 1, ,
4, 1, ,
9, 1, ,
10, 1, ,
13, 1, ,
14, 1, ,
17, 1, ,
.
.
.
— по сути, это перечисление всех узлов и номера степени свободы, по которой ограничивается перемещение данного узла.
5. Задание нагрузок
После того, как мы закрепили нашу балку, попробуем её нагрузить. Снова включим режим отображения граней и элементов
plot f beam
view edge off
view elem
Ориентируем изображение так, чтобы нам была видна верхняя часть незакрепленного конца балки
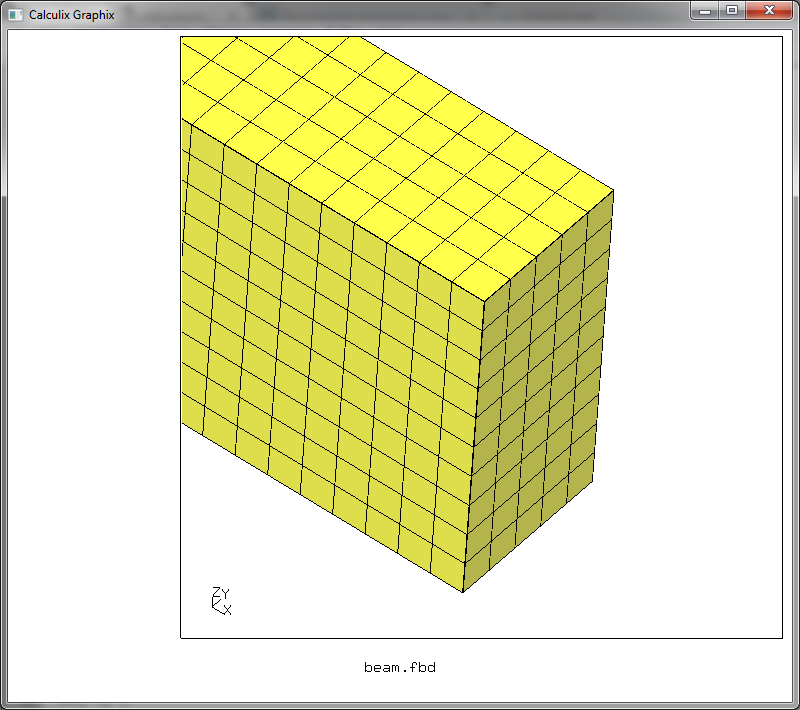
Перейдем в режим выделения объектов
qadd load
Наводим курсор на нужную грань и жмем f
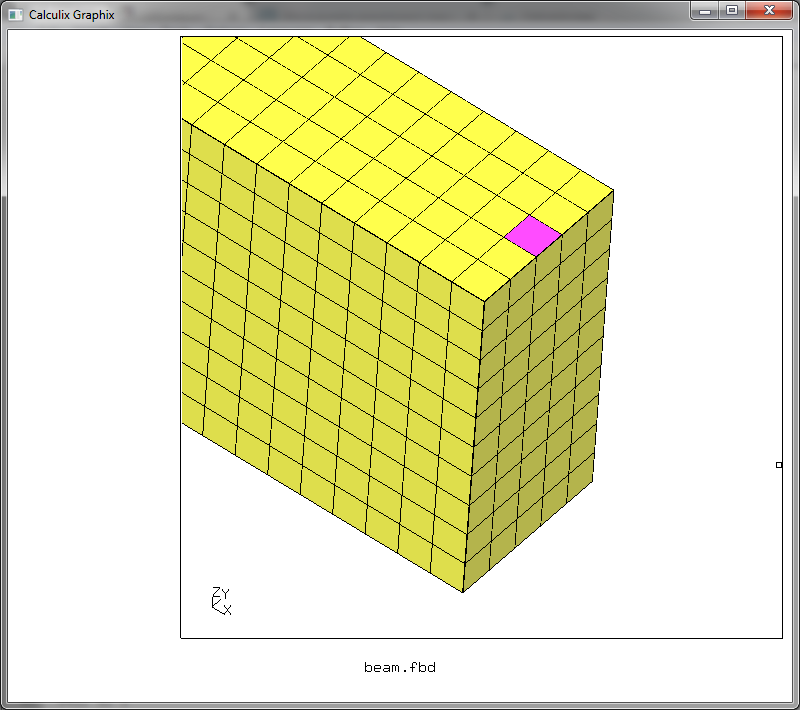
Грань подсвечивается фиолетовым, а в консольном окне появляется описание того, что она добавлена в набор load
qadd load
2541 e:3873 s:6 n= 5298 5310 5312 5300
Жмем a для окончания формирования набора, жмем q для выхода из режима выбора. К выделенной грани приложим давление, дающее равнодействующую силу величиной 10000 Н. Нетрудно посчитать, что площадь выделенной грани равна 1 см2, а значит искомое давление равно 108 Па. Задаем эту нагрузку командой
send load abq pres 1e8
— выводит нагрузку в файл load.dlo в формате ABAQUS. Файл выглядит так
** Pressure based on load
3873, P6, 100000000.000000
Указан номер элемента сетки, его грань и величина давления на эту грань. Таким образом, подготовку исходных данных можно считать завершенной.
6. Описание входных данных и запуск решателя
Все те данные — сетка, ограничения и нагрузки, следует теперь запулить на вход решателя МКЭ, для чего мы формируем входной файл такого вида
beam.inp
*HEADING
Model: CalculiX Beam Input File for Habrahabr article
*INCLUDE,INPUT=beam.msh
*BOUNDARY
*INCLUDE,INPUT=fixed_123.bou
*MATERIAL,NAME=EL
*ELASTIC
2e11,0.3
*SOLID SECTION,ELSET=Ebeam,MATERIAL=EL
*STEP
*STATIC
*DLOAD
*INCLUDE,INPUT=load.dlo
*NODE FILE
U
*EL FILE
S
*END STEP
Поясню подробнее, что тут к чему. Первая секция файла
*HEADING
Model: CalculiX Beam Input File for Habrahabr article
*INCLUDE,INPUT=beam.msh
задает описание задачи и включает файл с КЭ-сеткой beam.msh. Следующая секция формирует граничные условия — те связи, что мы определили в файле fixed_123.bou
*BOUNDARY
*INCLUDE,INPUT=fixed_123.bou
Не следует забывать и о материале, который мы задаем упругим, определяя его модуль Юнга и коэффициент Пуассона. Значения берем средние для конструкционных сталей
*MATERIAL,NAME=EL
*ELASTIC
2e11,0.3
*SOLID SECTION,ELSET=Ebeam,MATERIAL=EL
Последняя секция задает тип задачи — расчет статического нагружения и те нагрузки, из файла load.dlo который при этом действуют
*STEP
*STATIC
*DLOAD
*INCLUDE,INPUT=load.dlo
*NODE FILE
U
*EL FILE
S
*END STEP
Проверив, что мы имеем в SciTE открытой вкладку с файлом beam.inp жмем Ctrl + F10, запуская тем самым решатель. Получаем выхлоп, говорящий нам о том, что CalculiX что-то там для нас посчитал. Выхлоб, дабы не загромождать текст привожу под спойлером
CalculiX Version 2.10, Copyright© 1998-2015 Guido Dhondt
CalculiX comes with ABSOLUTELY NO WARRANTY. This is free
software, and you are welcome to redistribute it under
certain conditions, see gpl.htm
************************************************************
You are using an executable made on Mon May 23 13:24:06 2016
The numbers below are estimated upper bounds
number of:
nodes: 6666
elements: 5000
one-dimensional elements: 0
two-dimensional elements: 0
integration points per element: 8
degrees of freedom per node: 3
layers per element: 1
distributed facial loads: 1
distributed volumetric loads: 0
concentrated loads: 0
single point constraints: 198
multiple point constraints: 1
terms in all multiple point constraints: 1
tie constraints: 0
dependent nodes tied by cyclic constraints: 0
dependent nodes in pre-tension constraints: 0
sets: 2
terms in all sets: 18332
materials: 1
constants per material and temperature: 2
temperature points per material: 1
plastic data points per material: 0
orientations: 0
amplitudes: 2
data points in all amplitudes: 2
print requests: 0
transformations: 0
property cards: 0
STEP 1
Static analysis was selected
Decascading the MPC's
Determining the structure of the matrix:
number of equations
19800
number of nonzero lower triangular matrix elements
655236
Using up to 1 cpu(s) for the stress calculation.
Using up to 1 cpu(s) for the symmetric stiffness/mass contributions.
Factoring the system of equations using the symmetric spooles solver
Using up to 1 cpu(s) for spooles.
Using up to 1 cpu(s) for the stress calculation.
Job finished
7. Постпроцессинг и анализ решения
Полученные решателем результаты требует обработки постпроцессором. Для его вызова жмем Shift + F10 и получаем графическое окно с изображением балки. Кликаем в левой части этого окна, за рамкой с изображением балки и получаем меню
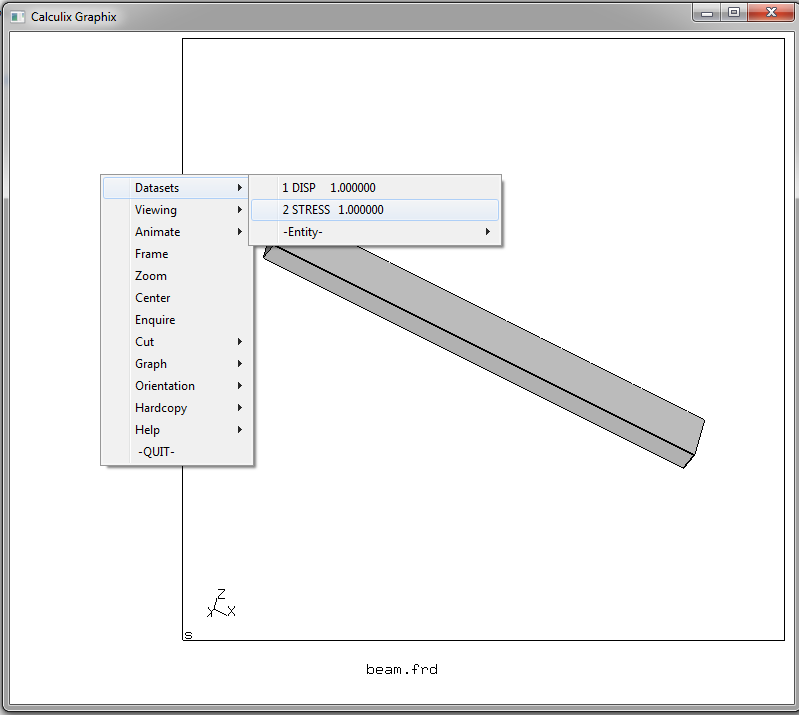
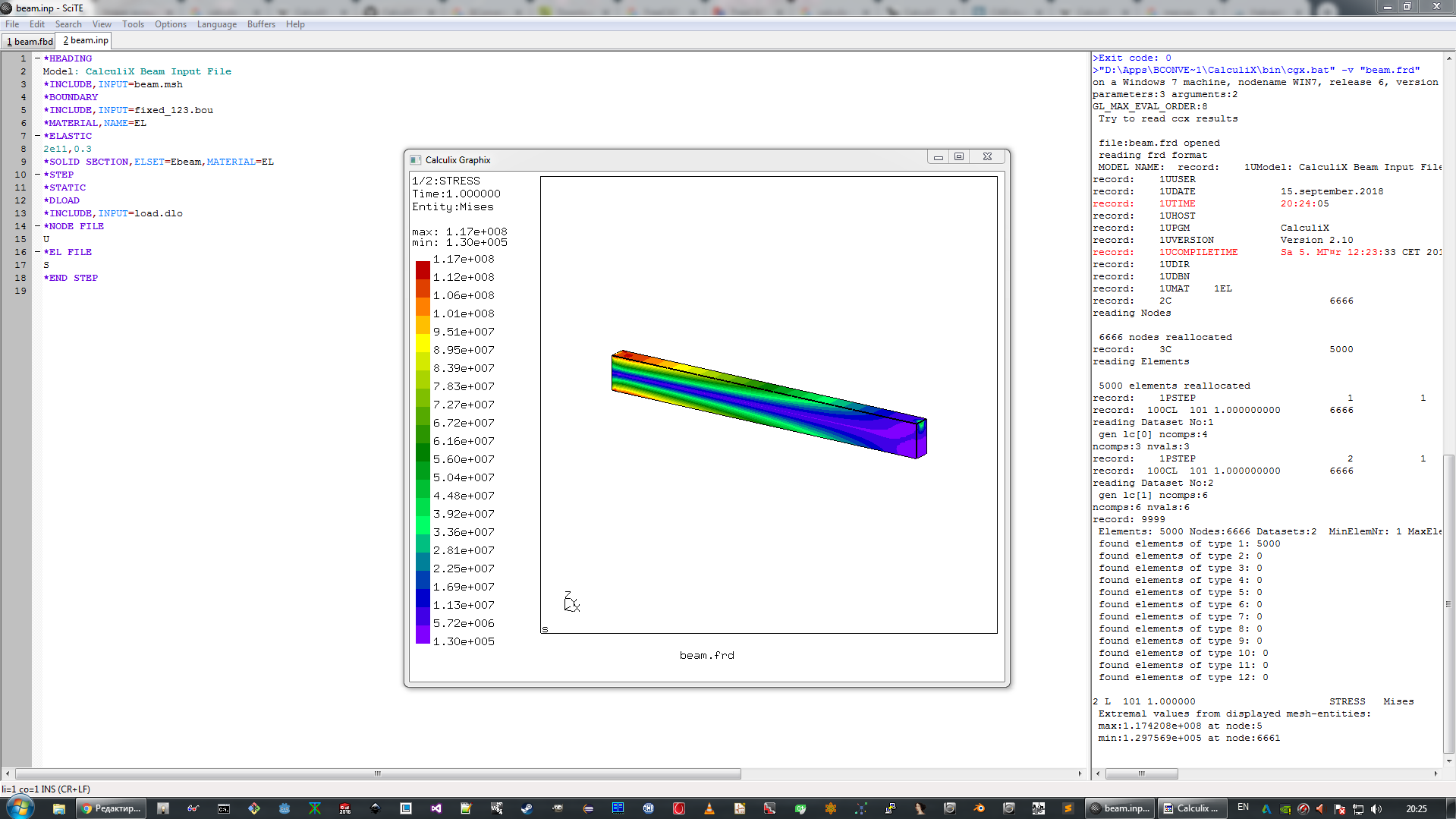
Что нас интересует? Напряжения в сечениях балки — выбираем Datasets -> STRESS. Меню исчезнет, но мы снова вызываем его и выбираем Datasets -> Entities -> Mises. В итоге включается режим отображения эквивалентных напряжений по фон Мизесу
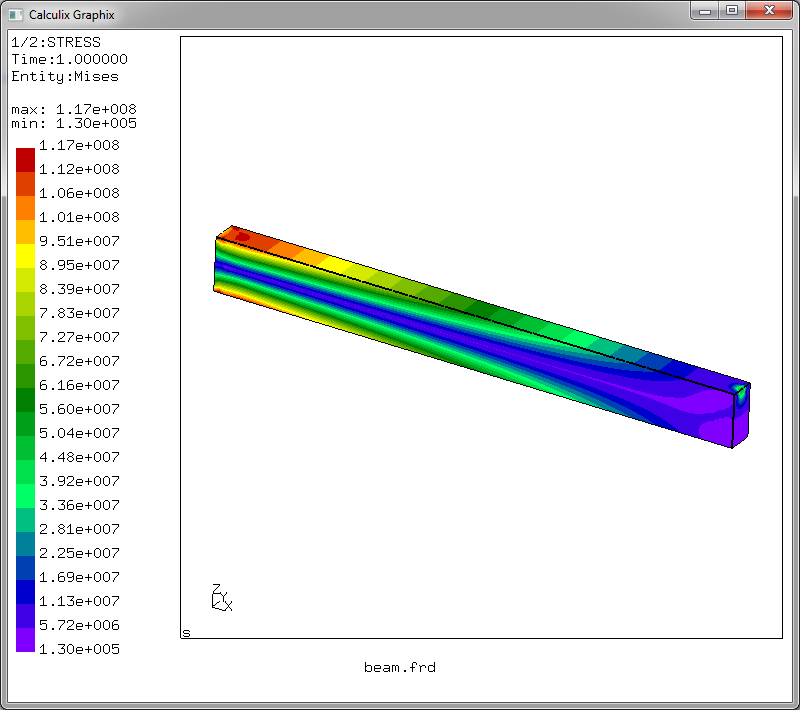
Итак — момент истины! Максимальное эквивалентное напряжение в сечении балки равно 117 МПа, что немного расходится с результатом из сопромата. Но! Решая задачу сопромата, мы не учитывали касательные напряжения при изгибе и сдвиге, а посчитали только нормальное напряжения от изгиба. Что будет с прогибом? Идем в меню: Datasets -> DISP и Datasets -> Entities -> D3
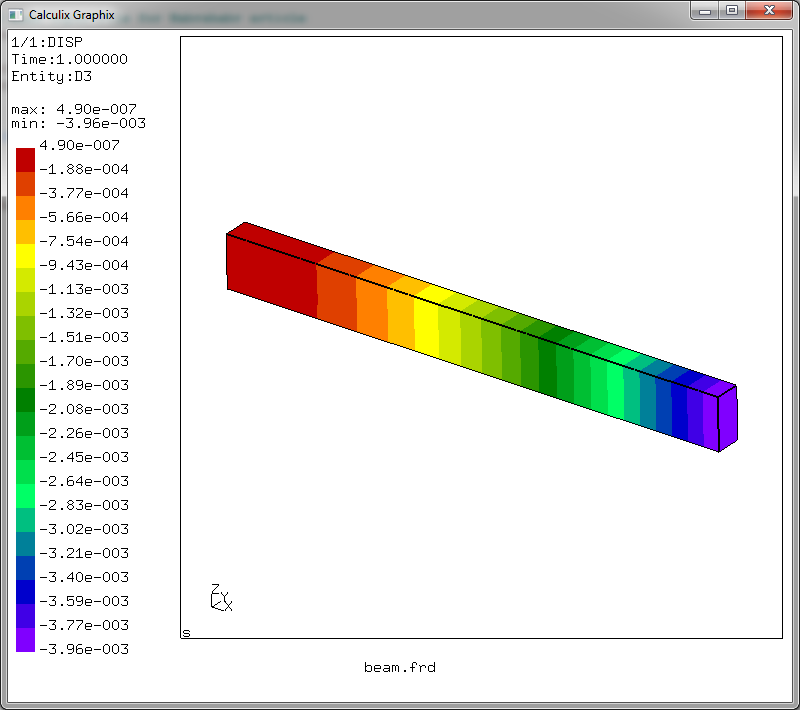
Наблюдаем, что максимальное перемещение соответствует нагруженному концу балки и равно оно 3,96 миллиметра! Великолепно и соотносится с нашим расчетом с использованием интеграла Мора.
Путем несложных манипуляций, о которых можно прочитать тут, генерируется и анимация деформаций балки
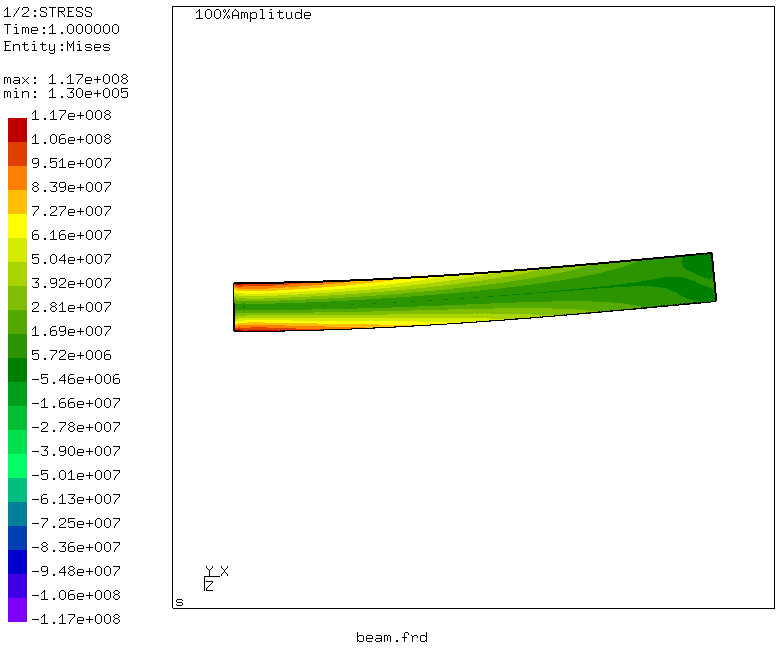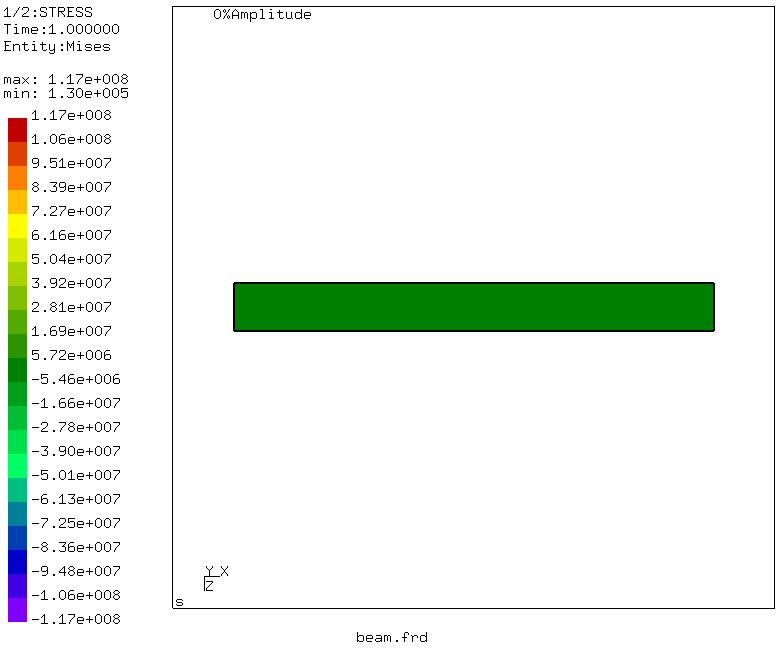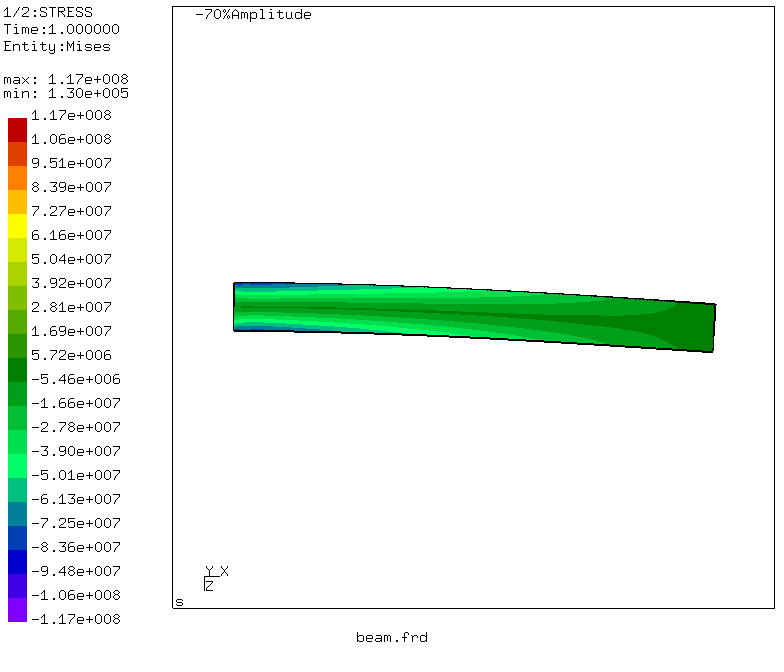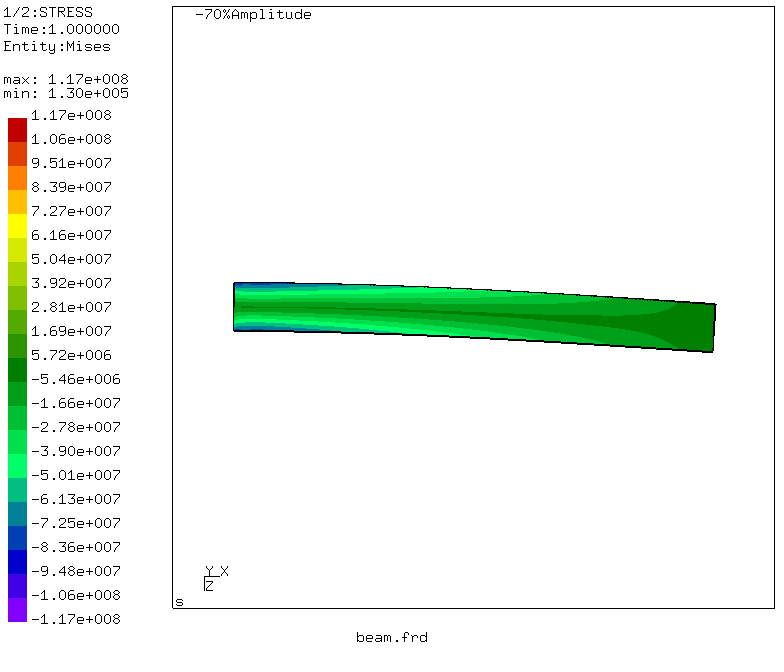
Делаем выводы
«Э-э-э, чувак, постой, а что же дальше?!». Хм, чувак не может вместить в одну статью всего того многообразия вопросов, что поднимаются при упоминании МКЭ в общем, и CalculiX в частности. Статья и так вышла объемистой и довольно занудной. И цель её — доходчивым языком объяснить две вещи:
- Open Source не прошел мимо ПО для МКЭ анализа
- Изучить и использовать данное ПО не так сложно, как может показаться на первый взгляд
Достаточно для обзорной статьи? Думаю да. При подготовке статьи использованы следующие источники:
- Calculix FEA Beam — послужило основой всего изложенного материала. Так как здесь добавлен опыт, полученный автором и весь код написан им в процессе написания статьи — это не перевод а именно тьюториал на русском языке
- Официальный мануал по CalculiX
Код примера доступен на Gitlab.
В заключении отмечу — я не прочнист, у меня не было сопромата в университете. Чуть позже, познать его самые основы меня заставила жизнь (и любовь!). Так что ляпы, возможно, присутствуют в тексте, о чем жду злобных комментов и даю обещание учесть все замечания.
Благодарю за внимание!
Автор: Дмитрий Притыкин
