В мае на Хабре была опубликована статья, которая повествует о работе Yitang Zhang в области теории простых чисел, вызвавшей большой резонанс в научном сообществе. В этой заметке даётся краткая сводка результатов, которых удалось достичь научному сообществу спустя девять месяцев с момента публикации этой работы.
Вспомним, что одной из важных, но до сих пор недоказанных, гипотез в теории чисел является гипотеза о простых числах-близнецах (twin prime conjecture), которая предполагает, что существет бесконечно много пар простых чисел, отличающихся на два, например: (3, 5); (11, 13) и т. д. При этом полагается, само собой, что существует бесконечно много простых чисел — факт, который был доказан ещё Евклидом. В более строгом виде, эта гипотеза о простых числах-близнецах может быть сформулирована следующим образом
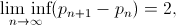
где 
обозначает n-ое простое число. Доказательство существования этого предела приводит к доказательству исходной гипотезы. Zhang был первым, кто смог представить доказатательство того, что существет конечная величина, обозначающая верхнюю границу величины интервала для бесконечного кол-ва пар простых чисел. Используя запись выше, результат Zhang может быть записан следующим образом
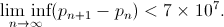
Тут важно сделать отступление и сказать что:
1. Это не значит, что все простые числа отстоят друг от друга на расстоянии меньше 70 000 000. На самом деле, чем больше n, тем больше среднее расстояние между двумя простыми числами и тем меньше вероятность встретить пару простых чисел, которые находятся на маленьком расстоянии друг от друга. Смотрите соответствующую статью в википедии на эту тему.
2. Это не значит, что взяв любое натуральное число, вы гарантировано обнаружите простое число в интервале плюс минус 70 000 000.
3. Доказательство состоит в том, что как бы далеко вы не зашли и какое бы большое натуральное число не взяли, всегда найдётся пара простых чисел, находящаяся дальше по оси, такая, что интервал между этими простыми числами будет меньше 70 000 000.
Эта работа вызвала большой резонанс и подтоклнула многих учёных к дальнейшему улучшению этой границы. Один из самых талантливых математиков современности Terence Tao с группой коллег организовал коллективный проект polymath8a, целью которого было снижение доказанной верхней границы. Буквально за несколько месяцев совместными усилиями удалось существенно улучшить результат Zhang и доказать, что
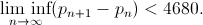
Результаты этой работы готовятся к публикации, хотя черновик (внимание, 177 страниц) можно прочесть уже сейчас.
19 ноября 2013 года последовал следующий прорыв. James Maynard доказал, что
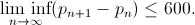
Гениальный Terence Tao не растерялся и огранизовал новый коллективный проект polymath8b, направленный на улучшение вновь полученной границы. Последний результат гласит, что
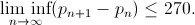
Таким образом известно, что существует бесконечное множество пар простых чисел, интервал между которыми не превышает 270. Потенциально эту границу можно уменьшить до 6, если удастся доказать другую гипотезу (в математике часто бывает, что доказательство одной гипотезы следует из доказательства/опровержения другой — так было, например, с теоремой Ферма).
Даже в этом случае, однако, это не приведёт немедленно к конечной цели — доказательству гипотезы простых чисел-близнецов, хотя и существенно приблизит математиков к ней.
Автор: Indalo
