Наверное, некоторые из вас слышали о такой головоломке, как Lights Out. Если кто-то не знает, суть вкратце такова: имеется поле из n x n клеток, часть клеток «включена», часть «выключена». При нажатии на клетку все клетки в области креста переключат своё состояние. Примерно так:


Собственно, задача — сделать все клетки поля «выключенными». Под катом кое-что интереснее, чем просто решение.
Сам алгоритм решения довольно нудный и объяснять его здесь долго. Вкратце — для поля каждого размера существует бинарная матрица A всех возможных ходов. Если представить изначальное поле в виде бинарного вектора X, то решение поля b — это решение системы бинарных линейных уравнений Ab = X. Нетрудно догадаться, что можно обратить матрицу A, сохранить её в переменной и находить решение уже любого поля по формуле b = A[sup]-1[/sup]X. Если кто-то хочет почитать подробнее, то здесь есть потрясающая статья, описывающая все нюансы. Мы двигаемся дальше.
К слову, решение существует не всегда для любой размерности. Размеры 5x5 или 17x17, например, решение имеют не всегда и в этой статье мы их не рассматриваем.
Генерация паттернов
Рассмотрим для примера следующее поле 20x20:

А теперь давайте посмотрим на его решение:

Красиво, правда? Давайте увеличим размер (и выключим границы, а то от них рябит в глазах). Возьмём, например, 75x75:

И посмотрим на его решение:

Довольно красиво. Но давайте не мелочиться, а сразу возьмём 150x150:

И его решением будет… Ух ты.
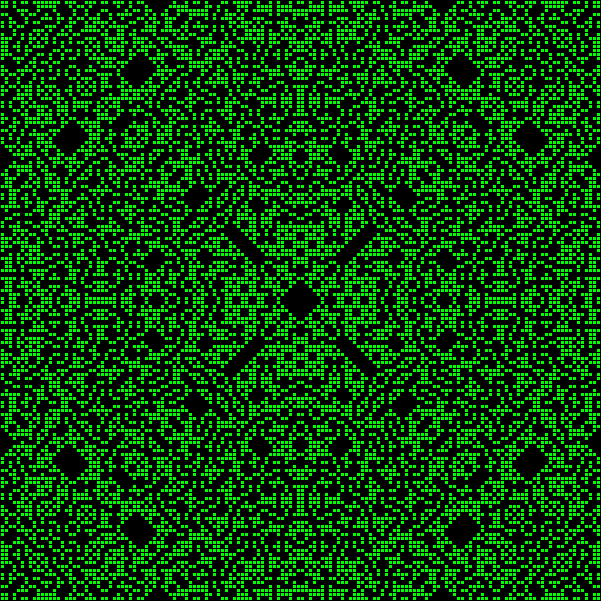
Завораживает. Издалека похоже на план города. Или на древнегреческую мозаику. Или на туркменский ковёр. Только почему-то зелёный.
А что будет, если попробовать получить решение для решения? Получим ещё один узор, производный. А потом можно сделать так ещё раз и получить ещё один производный узор.



При этом рано или поздно узоры зацикливаются. Для разных размеров разные периоды, при этом для чётных полей период больше, чем для нечётных (6x6 и 7x7, на больших размерах период уже в несколько сотен минимум):


При этом любой производный узор сохраняет любую осевую отражательную симметрию (анимации не зациклены, в зацикленной версии должно быть 2045 кадров):



Помимо отражательной, производный паттерн также способен сохранять и вращательную симметрию:

Хэши
Помимо паттернов, Lights Out можно использовать как медленную, криптографически нестойкую (из-за детерминистичности), но экзотическую хэш-функцию.
Как именно её считать? Ну, например, если считать всё поле начальным значением, то можно использовать в качестве хэша первые два столбца второго производного поля. Главную задачу хэш-функции они сохраняют — при небольшом изменении в начальных данных хэш меняется заметно. Вот, посмотрите сами:

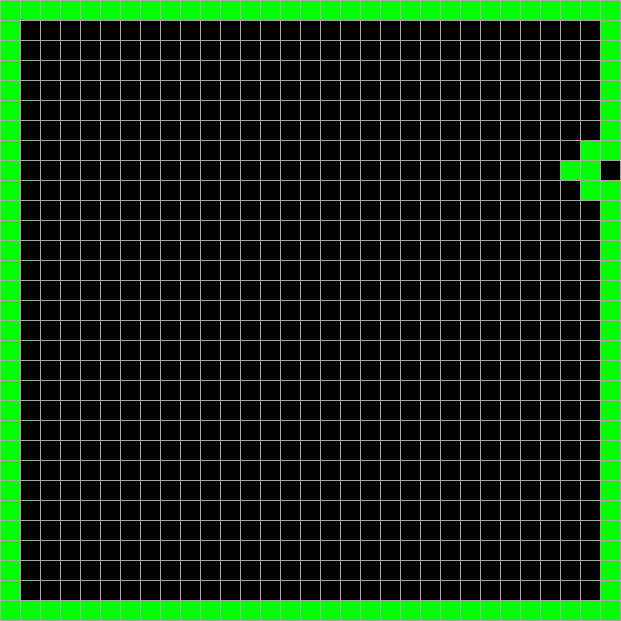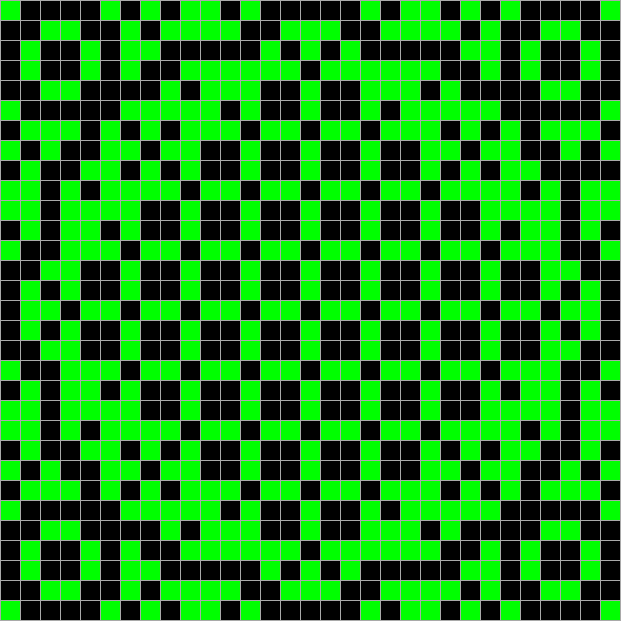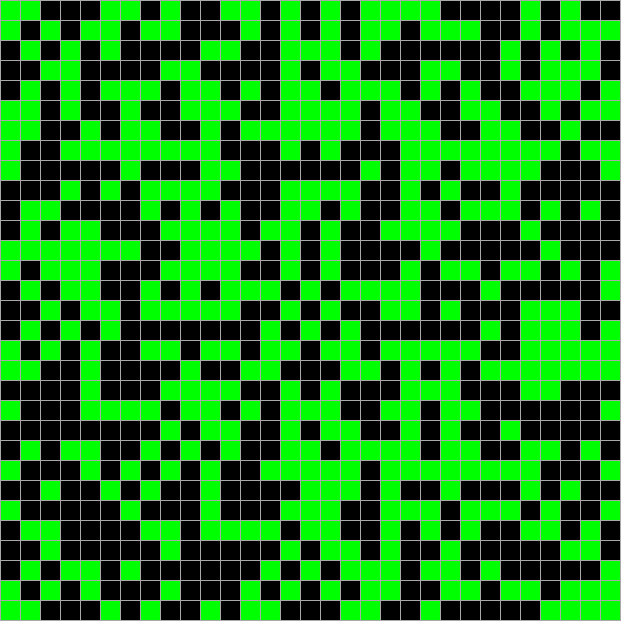
И только хэш:


Без анимации, чтобы заметить различие:


Где это можно применять? Ну, наверное, нигде. Для контрольных сумм он слишком медленный. В криптографии тоже не применить, потому что очень легко подобрать начальные данные, дающие данный хэш. Зато необычно.
Скрытие данных
Последнее применение — это скрытие данных внутри поля. Можно нарисовать на поле что-нибудь, затем несколько раз вычислить производный узор и выложить куда-нибудь. А благодаря цикличности изначально зашифрованное поле рано или поздно покажет себя. Вот пример (осторожно, гифка в 252 кадра). Если что, данные на 9-м кадре:

Приложение с исходниками на codeplex. К сожалению, пока есть версия только для Windows.
Автор: Sixshaman







