Здравствуйте, сегодня я хочу рассказать про метод геометрического параллелелизма для решения двумерного уравнения теплопроводности. Для наглядности, некоторые фрагменты будут реализованы при помощи MPI на языке C. Я постараюсь не повторяться с этой и этой статьями, и рассказать что-нибудь новенькое.
Постановка задачи
Двумерное уравнение теплопроводности задается уравнением:
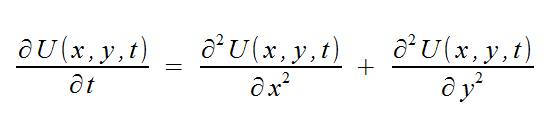
а также начальными условиями:
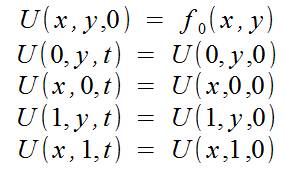
Также учитываем, что мы просчитываем ограниченную область пространства:
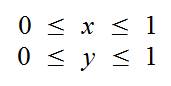
Итогом наших вычислений должен быть двумерный массив, содержащий значения функции U в узлах для некоторого значения времени. Можно решить уравнение аналитически, но это не наш вариант, и поэтому будем решать эту задачу численным методом. Для численного решения сделаем дискретизацию по времени, и получим координатную сетку в пространстве, а по времени получим набор «слоев». Для расчета будем использовать схему «крест».
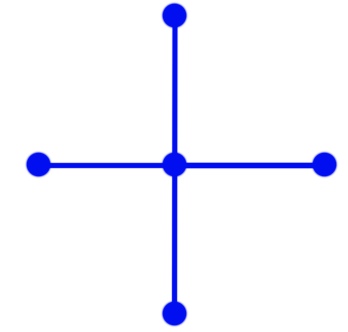
Если не вдаваться в подробности этой схемы, то по значению во всех точках «креста» на некотором «временном слое» получим значение в центральной точке на «следующем временном слое». Причем шаги по времени и координатам должны быть согласованны:
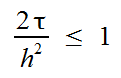
(здесь и далее сетка фиксированная и шаги по пространственным координатам равны h)
Для экономии памяти можно хранить только две сетки по X и Y, одну для текущего временного слоя и для следующего временного слоя. В таком случае после рассчета следующего временного слоя этот слой становится текущим, а в массив прошлого слоя записываются значения следующего временного слоя.
Метод геометрического параллелелизма
Метод геометрического параллелелизма используется для задач в которых можно выделить некоторую геометрическую закономерность и использовать ее для разделения работы между процессорами. В этой задаче сетка для ограниченного пространства можно изобразить как:

Параллелелизм в этом случае прослеживается довольно хорошо и можно разделить массив на несколько, и каждый новый отдать на рассчет своему исполнителю.
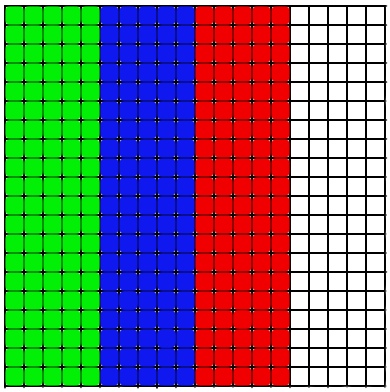
Вообще-то можно разделить массив и на горизонтальные полосы, принципиальных различий для метода это не внесет, а про различия в реализации скажу позже. Таким образом каждый исполнитель будет считать только свой участок массива.
Подводные камни
Если вернуться к разностной схеме, по которой будем производить рассчет, то становится ясно, что это еще не конец. Из схемы видно, что для рассчета любого элемента сетки нам необходимо знать элементы сбоку от него на предыдущем слое. Это означает, что крайний слой пространственной сетки просчитать не сможем (так как не хватает данных), но если взглянуть на граничные условия, то видно что крайние элементы известны из условий. Но появляется проблема расчета элементов на границе областей исполнителей. Ясно, что придется в процессе пересылать данные между соседними исполнителями. Это можно сделать в виде цикла, который передает по элементу:
for (int i = 0; i < N; i ++)
{
MPI_Send(*buf, 1, MPI_DOUBLE, toRank, MESSAGE_ID, MPI_COMM_WORLD);
}
(подробнее про передачу по элементам можно прочитать в статьях, упомянутых в начале)
Этот способ не эффективен, поскольку придется устанавливать много соединений(это занимает большое время). Наши потребности может удовлетворить создание пользовательского типа данных. Кроме создания пользовательских структур, MPI может предложить нам несколько видов «масок» для данных: MPI_Type_contiguous и MPI_Type_vector. Первый из них создает тип, описывающий несколько элементов, подряд расположенных в памяти, а второй позволяет создать «шаблон» по которому из последовательно расположенных в памяти элементов выбираются «нужные» элементы, потом пропускаются «ненужные» и повторяется выбор нужных. Их количество фиксированное.
// Первый аргумент - количество элементов в новом типе, для этого случая равно количеству строк
// Второй аргумент - количество "нужных" элементов
// Третий аргумент - период повторения шаблона, для этого случая равно количеству столбцов
MPI_Datatype USER_Vector;
MPI_Type_vector(N, 1, N, MPI_DOUBLE, &USER_Vector);
// В конце не забыть "опубликовать" свой тип
MPI_Type_commit(&USER_Vector);
Если отправить этот тип, а в качестве *buf указать начало массива, то получится:
+ 0 0
+ 0 0
+ 0 0
Если указать как *buf второй элемент массива, то получим:
0 + 0
0 + 0
0 + 0
Так можно передать (и принять) только один столбец массива, причем за один вызов MPI_SEND:
MPI_Send(*buf, 1, USER_Vector, (rank + 1), MESSAGE_ID, MPI_COMM_WORLD);
Если расположить зоны исполнителей горизонтально, то можно использовать MPI_Type_contiguous или в MPI_Send указывать необходимое число элементов, но это, на мой взгляд, красивее.
Теперь надо понять в каком порядке пересылать эти столбцы. Самый очевидный: пусть исполнители по очереди передают нужный столбец нужному получателю. Тогда получим следующую картину:
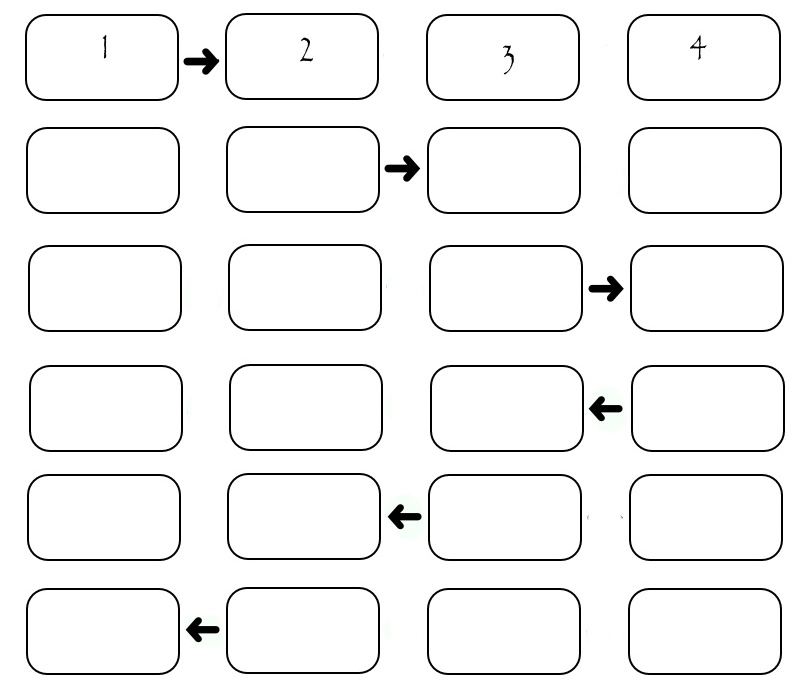
Хоть иллюстрация показывает обмен только между четырьмя исполнителями, можно посчитать, что если на одну передачу затрачивается некоторое SEND_TIME, то для передачи всех столбцов необходимо (2*N-2)*SEND_TIME. Видно, что во время передачи каждого столбца «работают» только два исполнителя, а остальные простаивают. Это не хорошо. Рассмотрим немного измененную схему: в ней исполнители разделены по «четности» их номера. Сначала все четные передают столбец исполнителю с большим номером, потом все четные передают столбец исполнителю с меньшим номером, потом аналогичным образом поступают исполнители с нечетными номерами. Конечно все пересылки происходят только при наличии того, кому пересылать.
// EVEN_RIGHT, ODD_RIGHT, ODD_LEFT, EVEN_LEFT - некоторые константы для разделения сообщений
// (на всякий случай, а также для большей осмысленности кода)
const int ROOT = 0;
if ((rank % 2) == 0)
{
if (rank != (size - 1))
MPI_Send(*buf, 1, USER_Vector, (rank + 1), EVEN_RIGHT, MPI_COMM_WORLD);
if (rank != ROOT)
MPI_Recv(*buf, 1, USER_Vector, (rank - 1), ODD_RIGHT, MPI_COMM_WORLD, &status);
if (rank != (size - 1))
MPI_Recv(*buf, 1, USER_Vector, (rank + 1), ODD_LEFT, MPI_COMM_WORLD, &status);
if (rank != ROOT)
MPI_Send(*buf, 1, USER_Vector, (rank - 1), EVEN_LEFT, MPI_COMM_WORLD);
}
if ((rank % 2) == 1)
{
MPI_Recv(*buf, 1, USER_Vector, (rank - 1), EVEN_RIGHT, MPI_COMM_WORLD, &status);
if (rank != (size - 1))
MPI_Send(*buf, 1, USER_Vector, (rank + 1), ODD_RIGHT, MPI_COMM_WORLD);
MPI_Send(*buf, 1, USER_Vector, (rank - 1), ODD_LEFT, MPI_COMM_WORLD);
if (rank != (size - 1))
MPI_Recv(*buf, 1, USER_Vector, (rank + 1), EVEN_LEFT, MPI_COMM_WORLD, &status);
}
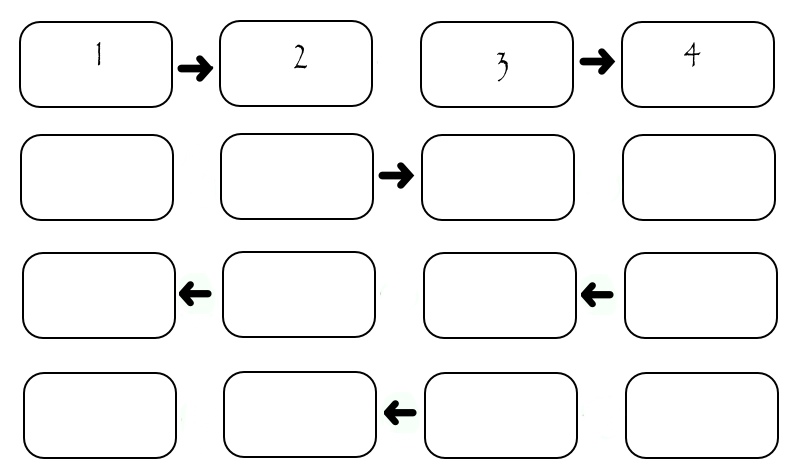
В данном случае передача занимает ровно 4*SEND_TIME вне зависимости от количества исполнителей. На системах с множеством исполнителей это несет в себе значительное превосходство.
(На рисунках про передачу присутствует некоторая ложь: номера исполнителей начинаются с нуля, как в массиве, а на рисунках они пронумерованы в «обычном» порядке: начиная с первого. Т.е. отняв единицу от номера на рисунке получим его номер в программе)
Автор: vasikos








