Многие считают, что сложнее классической физики может быть только квантовая. Однако куда сложнее изучать системы, которые находятся, так сказать, на стыке этих двух миров. Если в квантовую систему добавлять все больше и больше частиц, то она начнет терять свои квантовые свойства и превращаться в более классическую. Этот процесс именуют квантово-классическим переходом. Чтобы изучить такую систему, классических компьютеров будет недостаточно, потому ученые из Лос-Аламосской национальной лаборатории предложили свой собственный алгоритм, который в сопряжении с квантовыми компьютерами из пары сотен кубитов сможет разгадать тайны квантово-классического перехода. Как работает алгоритм, почему меньше формул значит лучше и какое применение сего алгоритма на практике? Об этом и не только мы узнаем из доклада исследовательской группы. Поехали.
Основа исследования
Квантово-классический переход, если утрировано, это процесс декогеренции, когда квантовая система теряет свою когерентность, то есть приобретает классические черты. Этот процесс может возникать по ряду причин, среди которых самой очевидной является взаимодействие квантовой системы и окружающей среды. Также считается, что именно этот процесс является камнем, о который спотыкается процесс реализации реального квантового компьютера.
Методов борьбы с декогеренцией много, один занятнее другого, но суммарно их можно разделить на две категории: изоляция и внедрение. В первом случае ученые стараются изолировать квантовую систему от воздействия окружающей среды, применяя очень низкие температуры и/или высокий вакуум. Во втором случае в алгоритмы квантовых расчетов вносят правки (код), которые будут устойчивы к ошибкам, возникающим ввиду декогеренции. Данные методы работают, этого никто не отрицает, но они не очень масштабируются. Ученые могут удерживать атомы в состоянии суперпозиции какое-то время, если влияние окружающей среды минимизировано. Однако на более крупном масштабе все, как правило, идет к чертям собачьим.
Итак, пока одни мозговитые люди в белых халатах ищут способы борьбы с декогеренцией, другие ищут инструменты для ее изучения. Хочешь победить своего врага — знай его в лицо, как говорят.
Прежде, чем мы окунемся в поток формул и пояснений касательно разработанного учеными алгоритма, стоит совершить небольшой временной скачок. Роберт Гриффитс, американский физик из университета Карнеги-Меллон, в 1984 году предложил теорию последовательных историй (событий): классическая физика приближена к квантовой механике, а квантовая математика может рассчитать вероятности крупномасштабных и субатомных явлений, которые относятся не к результатам измерений, а к физическому состоянию системы. Мистер Гриффитс приводит в пример фотографии горы, которые можно сделать из разных ракурсов, а потом из них составить картину реальной горы. В случае квантовой физики можно выбрать параметр измерений, но совместить два измерения, чтобы составить цельную картинку частицы до измерения, не выйдет. До фактического процесса измерения реального положения и импульса просто не существует.

Роберт Гриффитс
Запутанно и немного сносит крышу, но это еще не все. В 1989 году Мюррей Гелл-Манн и Джеймс Хартл на основе теории Гриффитса выдвинули свою собственную. По их мнению можно рассматривать всю Вселенную как единую квантовую систему без внешней среды. Если так, то декогеренция протекает внутри системы, а результатом ее активности являются квазиклассические домены — наборы последовательных историй, неразличимые на фоне грубой зернистости из-за декогеренции.
Данные теории помогали решить некоторые проблемы и парадоксы в квантовой механике, однако далеко не все. Исследователи считают, что данные умозаключения их предшественников не получили широкого применения ввиду того, что расчеты нетривиальных систем (например, дискретных систем заметного размера или непрерывных систем, которые не допускают приближенных описаний точно решаемыми интегралами) являются крайне сложными. Другими словами, эти теории хороши, но лишь в простых случаях.
В последние годы развитие квантовых технологий сильно ускорилось, и появились вариационные гибридные квантово-классические алгоритмы (VHQCA), которые отлично справляются с разными задачами (факторинг, поиск основных состояний и т.д.).
В рассматриваемом нами сегодня труде ученые описывают свой VHQCA алгоритм для последовательных историй. По словам исследователей, их алгоритм превосходит классические методы по многим параметром, в том числе и по размерам изучаемых систем.
Марафон формул (расчетно-теоретическая база)
У нас уже было историческое отступление, а теперь стоит немного ознакомиться с вычислительной базой алгоритма прежде, чем рассмотреть результаты его работы.
В основе последовательных историй (CH) история Yα представляет собой последовательность свойств в последовательности моментов времени t1 < t2 < … < tk:
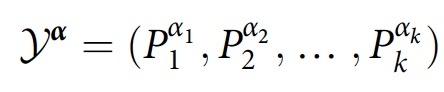
где Pαjjвыбирается из множества проекторов Pj, которые суммируются в момент времени tj.
Ученые приводят поясняющий пример: фотон, проходящий через несколько дифракционных решеток и затем ударяющийся по экрану. В такой ситуации историей может быть фотон, прошедший через одну щель в первой решетке, другую щель во второй и т.д. Следовательно, существует некая интерференция между такими историями. А поскольку существуют помехи, то нельзя классически сложить вероятности различных историй в ожидании верного предсказания точки попадания фотона на экран.
Каркас CH предоставляет инструменты для определения того, когда семейство историй F = {Yα} демонстрирует интерференцию, что не всегда очевидно. В нем также определяется оператор класса:
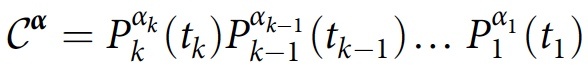
что является упорядоченным по времени продуктом операторов проекции в истории Yα. Если система первоначально описывается матрицей плотности ρ, степень интерференции или перекрытия между историями Yα и Yα′ будет равна:
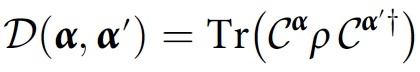
Данная величина называется функционалом декогеренции. Условие согласованности для семейства историй F в таком случае будет выглядеть так:

Только в том случае, если это условие выполняется, для истории Yα вероятностью будет D(α, α). Для более упрощенных расчетов можно применить другое условие:

Ученые говорят, что для численного алгоритма крайне полезным будет рассмотрение приблизительной согласованности при учете незначительных помех:

Для изучения согласованности, возникающей исключительно из декогеренции (то есть записи в среде), исследователи предложили способ, который вместо этого берет частичный след над E, который является подсистемой среды:

С этой модификацией условие согласованности будет выглядеть следующим образом:

где 0 — нулевая матрица. Вместо обозначения отсутствия вмешательства внешней среды, согласованность указывает на наличие/отсутствие противоречий в записях историй в окружающей среде.

Изображение №1: схема разветвления историй за k временных шагов.
Учитывая марафон формул и понимание последовательных историй, ученые указывают на очевидность того факта, что классические численные схемы для СН не способны справиться с задачей.
На изображении выше показан пример, где есть истории совокупности n-ого числа частиц с 1/2 спином для k временных шагов. Количество историй составляет 2nk, следовательно, существует ~ 22nk функциональных элементов декогеренции. Кроме того, оценка каждого функционального элемента декогеренции D(α, α’) требует эквивалента гамильтоновой симуляции системы, то есть умножение 2n х 2n матриц. Это значит, что современным кластерам понадобятся сотни лет, чтобы рассчитать согласованность семейства историй с k = 2 временными шагами и n = 10 спинами.
Гибридный алгоритм VCH
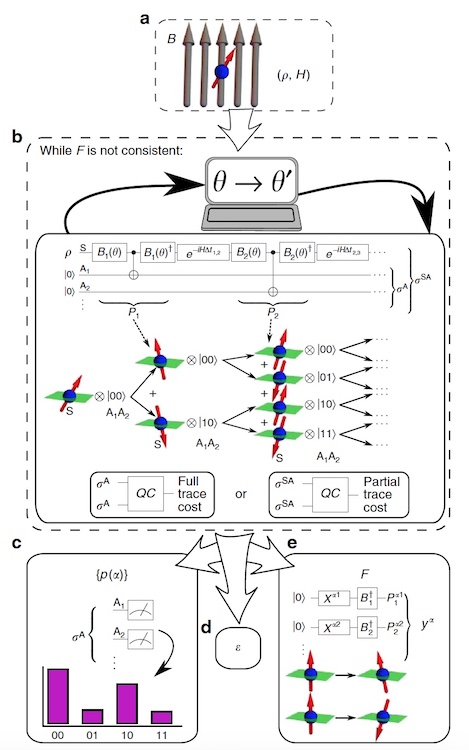
Изображение №2: Блок-схема VCH.
Свой VHQCA алгоритм ученые назвали VCH (вариативные последовательные истории). VCH принимает в качестве входных данных физическую модель (то есть начальное состояние ρ и гамильтониан H) и некоторый анзац* для типов проекторов, которые необходимо рассмотреть.
Анзац* — догадка о том, каким должно быть решение уравнения и какую форму оно должно иметь.
В качестве результирующих данных имеется следующее:
- семейство историй F, которое (приблизительно) является полным и/или частичным следом в форме проекционных операторов, подготовленных на квантовом компьютере;
- вероятности наиболее вероятных историй Yα в F (простите за каламбур);
- оценка параметра согласованности ε.
VCH включает в себя цикл оптимизации параметров, где квантовый компьютер оценивает функцию затрат, которая количественно определяет несоответствие семейства, в то время как классический оптимизатор настраивает семейство (то есть изменяет параметры проектора), чтобы снизить затраты.
Для расчета затрат необходимо учитывать, что элементы функционала декогеренции образуют положительную полуопределенную матрицу. Это свойство используется в VCH для кодирования D в квантовом состоянии σA, матричными элементами которого являются ⟨α | σA | α′⟩ = D(α, α′).
На 2b показана квантовая схема, которая подготавливает σA, преобразуя начальное состояние ρ ⊗ | 0〉 〈0 | в системах SA (где S моделирует интересующую физическую систему, а A является вспомогательной системой) в состояние σSA, предельное значение которого σA.
Для согласованности полного следа матрицы вводится глобальная мера согласованности, которая количественно определяет, насколько далеко σA от диагонали, которая служит функцией затрат:

где DHS — расстояние Гильберта-Шмидта и ZA(σA) — дефазная (все недиагональные элементы установлены в ноль) версия σA.
Эта величина стремится к нулю тогда и только тогда, когда F согласован. Для случая частичного следа получается аналогичная функция затрат, но с заменой σA на σSA:
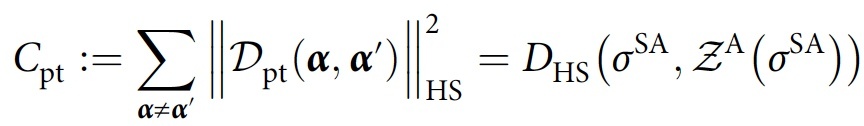
Цикл оптимизации параметров приводит к приблизительно согласованному семейству историй F, где параметр согласованности ε ограничен сверху в рамках конечных затрат.
На 2с показана генерация вероятности для наиболее вероятных историй путем многократной подготовки σA и измерения на стандартной основе, где частоты измерений дают вероятности.
На 2е показано как подготовить набор операторов проекции для любой заданной истории в F.
Результаты экспериментов
Было проведено несколько различных экспериментов с применением VCH алгоритма. Мы рассмотрим два — спин в магнитном поле и хиральная молекула.
Спин в магнитном поле

Изображение №3
В первом эксперименте рассматривались две временные истории частицы со спином 1/2 в магнитном поле Bz, гамильтониан которой равен H = -γBσz. Рассматриваемые нами истории имеют временной шаг Δt между начальным состоянием и первым проектором, а также между первым и вторым проектором. Помимо этого, стоит отметить, что рассматриваются только проекторы на плоскости xy сферы Блоха.
На изображении выше показана диаграмма затрат для квантового процессора ibmqx5, а также для симулятора, точность которого была ограничена наложением той же конечной статистики, которая была собрана с помощью квантового процессора. Несколько минимумов, найденных при запуске VCH на ibmqx5, накладываются на диаграмму. Поскольку эти минимумы достаточно хорошо соответствуют теоретически согласованным семействам, это представляет собой успешность реализации VCH на практике.
Хиральная молекула

Изображение №4
Хиральная молекула была выбрана для практических опытов, поскольку это отличный способ определить пути применения VCH. Хиральная молекула была смоделирована как двухуровневая система, в которой правое |R〉 и левое |L〉 состояния хиральности описываются как |R⟩/|L⟩ = |+⟩/|-⟩=1/√2 * (|0⟩ ± |1⟩).
Изолированная хиральная молекула туннелирует между |R⟩ и |L⟩, однако ученые предполагают, что она находится в газе, где столкновения с другими молекулами передают информацию о хиральности молекулы в ее окружающую среду. Эта передача информации моделируется вращением на угол θx вокруг оси x кубита среды, контролируемой хиральностью системы.
Затем ученые рассматривают простые семейства стационарных историй, где набор проекторов соответствует одному и тому же основанию все пять раз (для простоты моделирования было установлено, что молекула сталкивается с другими молекулами 5 раз). Предположим, что θz это угол прецессии из-за туннелирования во времени между столкновениями, тогда возможно исследовать конкуренцию между декогеренцией и туннелированием. На изображении выше продемонстрированы результаты данного моделирования.
Ученые отмечают любопытный факт — имеет место переход от квантового режима, где хиральность не является последовательной, к классическому режиму, где хиральность является как последовательной, так и стабильной во времени.
Для более детального ознакомления с нюансами исследования рекомендую заглянуть в доклад ученых и дополнительные материалы к нему.
Эпилог
Данный труд продемонстрировал новый алгоритм, который в сопряжении с имеющимися и будущими квантовыми вычислительными машинами может лучшим образом описать столь сложный и запутанный процесс как квантов-классический переход. Исследование этого явления имеет большую важность, если мы когда-нибудь хотим создать реальный, работающий и эффективный квантовый компьютер, на работу которого не будет влиять декогеренция.
VCH алгоритм находится на начальной стадии разработки, но уже показывает свою работоспособность. В дальнейшем ученые намерены, естественно, совершенствовать его. Как бы то ни было, перспективы скорой реализации квантовых вычислений не просто остаются на прежнем уровне, а растут с каждым таким исследованием.
Благодарю за внимание, оставайтесь любопытствующими и хорошей всем рабочей недели, ребята! :)
Спасибо, что остаётесь с нами. Вам нравятся наши статьи? Хотите видеть больше интересных материалов? Поддержите нас оформив заказ или порекомендовав знакомым, 30% скидка для пользователей Хабра на уникальный аналог entry-level серверов, который был придуман нами для Вас: Вся правда о VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps от $20 или как правильно делить сервер? (доступны варианты с RAID1 и RAID10, до 24 ядер и до 40GB DDR4).
Dell R730xd в 2 раза дешевле? Только у нас 2 х Intel TetraDeca-Core Xeon 2x E5-2697v3 2.6GHz 14C 64GB DDR4 4x960GB SSD 1Gbps 100 ТВ от $199 в Нидерландах! Dell R420 — 2x E5-2430 2.2Ghz 6C 128GB DDR3 2x960GB SSD 1Gbps 100TB — от $99! Читайте о том Как построить инфраструктуру корп. класса c применением серверов Dell R730xd Е5-2650 v4 стоимостью 9000 евро за копейки?
Автор: Dmytro_Kikot