Общеизвестно, что большинство временных рядов, с которыми приходится иметь дело исследователю, являются нестационарными, и их анализ ощутимо сложнее, чем изучение стационарных процессов. Поскольку интерес к вейвлетам, похоже, пошел на убыль, полезно обсудить некоторые иные «нестационарные» инструменты, пригодные, в первую очередь, для оценки мгновенных частот, а также для оценки мгновенных спектров.
В первую очередь есть смысл вспомнить об «аналитическом сигнале». Ниже «An-моделью» именуются как раз нахождение мгновенных импеданса и мощности тестового сигнала после достройки его мнимой частью (сдвинутой по фазе на π/2).
Но не всегда есть возможность возиться с преобразованием Гилберта. Ранее уже упоминалось об авторегрессионном способе спектрального оценивания, пригодном для работы с короткими последовательностями. Под «AR-моделью» здесь будет подразумеваться исследование коротких (из 5 сэмплов) перекрывающихся фрагментов исходного сигнала с целью определения коэффициентов авторегрессии 2-го порядка, нахождение по ним «полюсов» модели и т.д.
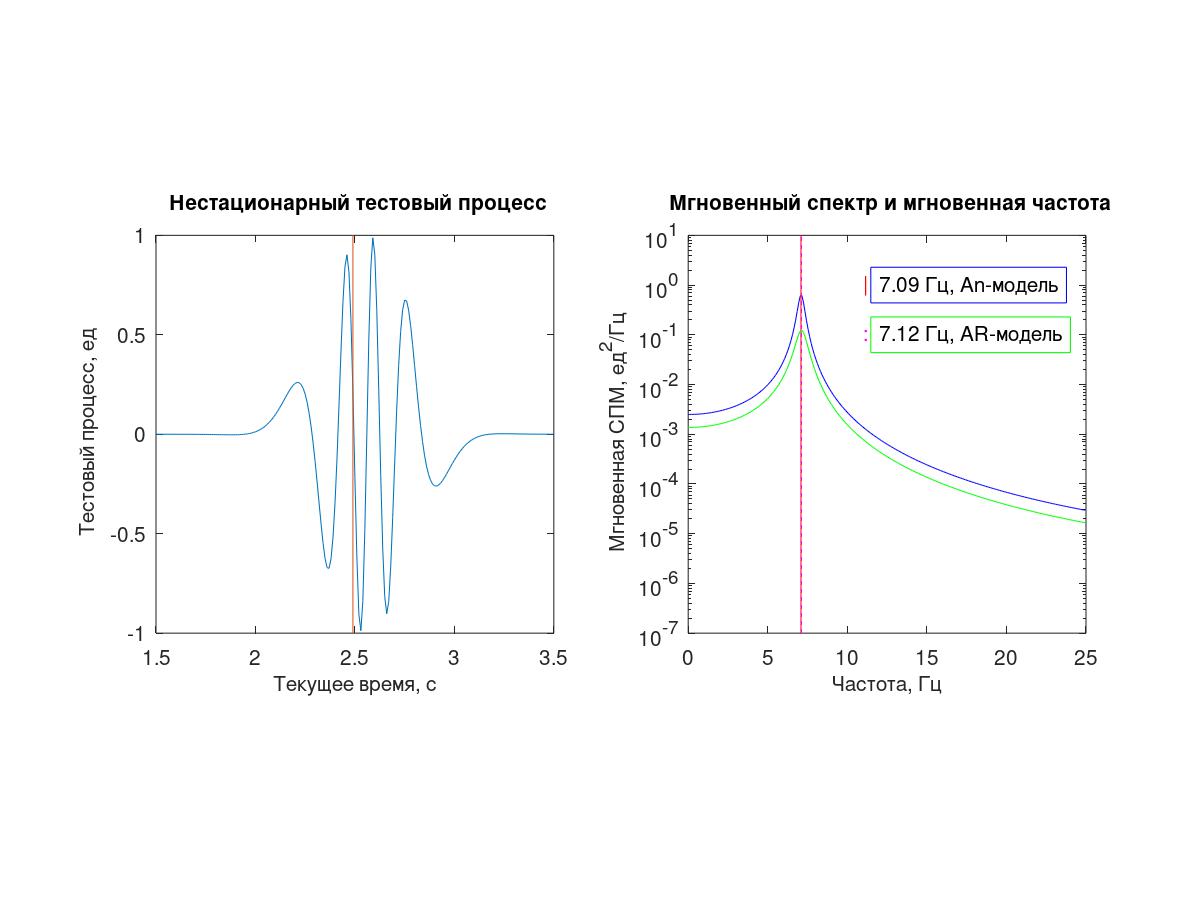
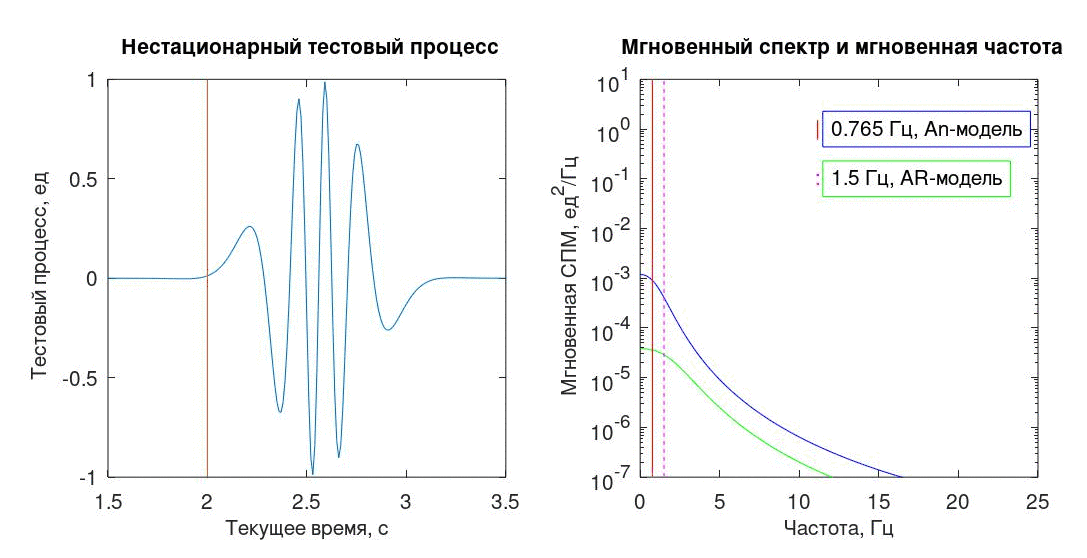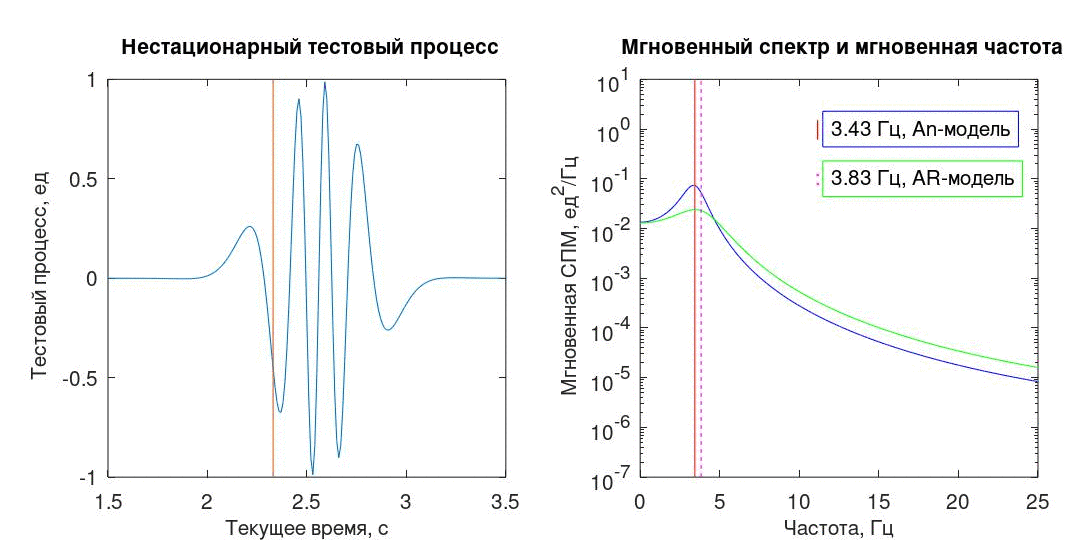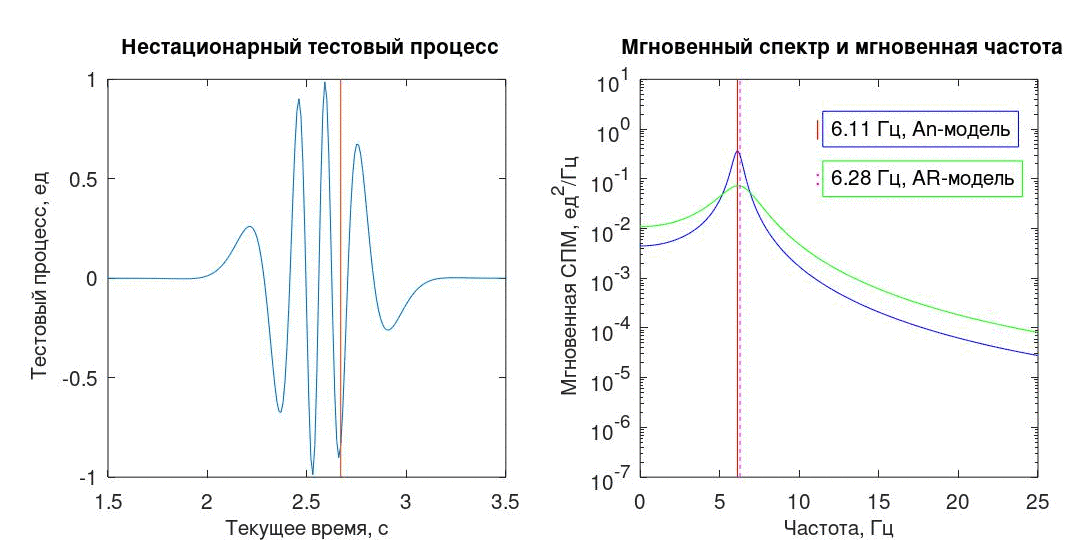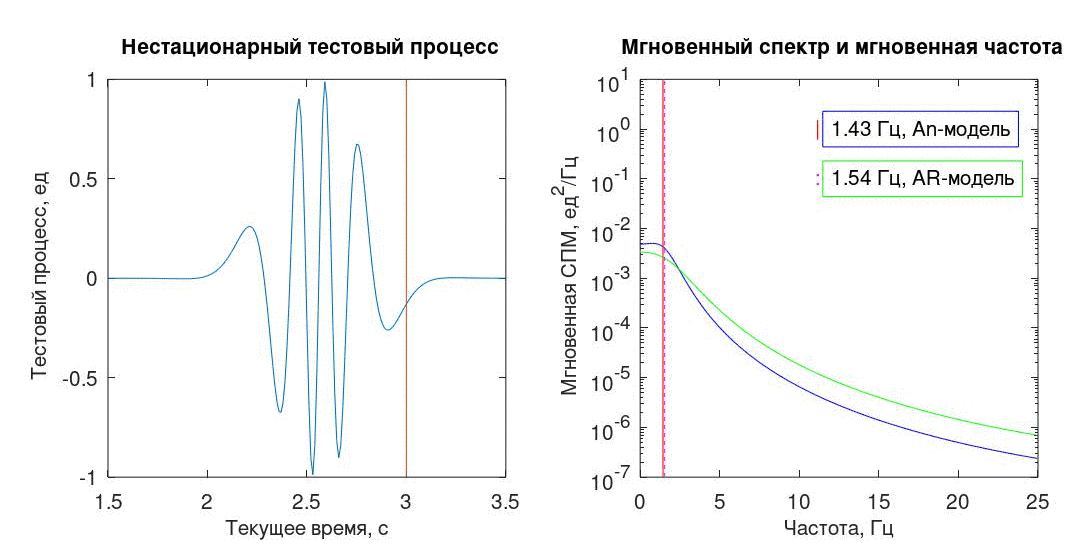
Оба изложенных здесь метода основаны на одном принципе — предположении, что в некоторой малой окрестности от выбранного момента времени исследуемый процесс может быть аппроксимирован «экспоненциальной» последовательностью — одной комплексной (An) или суммой двух комплексно-сопряженных экспонент (AR).
В качестве тестового процесса использована последовательность из 512 отсчетов с условным интервалом дискретизации Δt=0,01с, полученная из непрерывного детерминированного процесса (1).
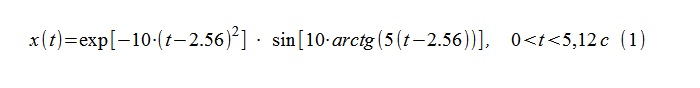
«Логарифмированием» и последующим дифференцированием соответственно высокочастотного наполнения и огибающей из (1), получены теоретические выражения для (мгновенных) частоты и декремента (2)
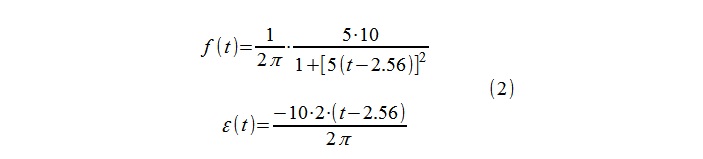
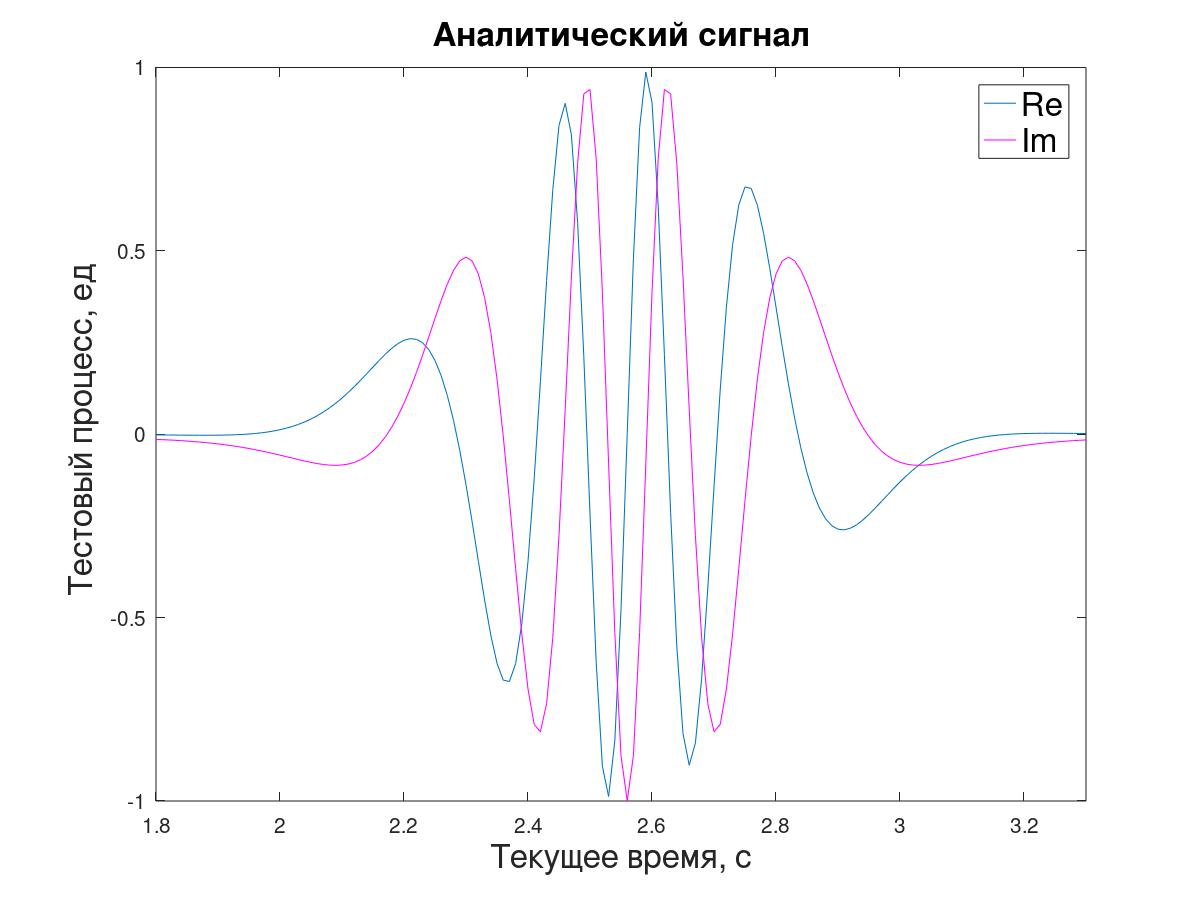
Для An-моделирования периодограммным методом (прямым и обратным преобразованием Фурье) из исходной последовательности x[i] сформирован аналитический сигнал y[i].
Отношение двух последовательных отсчетов такого сигнала, в принципе, позволяют определить мгновенный импеданс λ, но для упрощения данной демонстрационной задачи — чтобы не возиться с созданием промежуточных отсчетов или объяснением сдвига оценки на Δt/2 — решено работать с отсчетами «через один», вычисляя λi по отношению последующего y[i+1] значения сигнала к предыдущему y[i-1] (3).
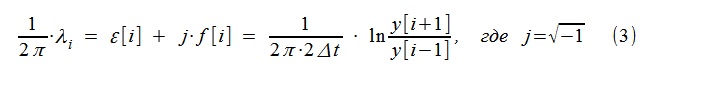
Для AR-моделирования (модель второго порядка) применена стандартная процедура вычисления автокорреляционных коэффициентов 1, a1i, a2i с помощью уравнений Юла-Уолкера, при этом в качестве исходного процесса принимались 5-сэмпловые последовательности x[i-2], x[i-1],… x[i+2] (4).
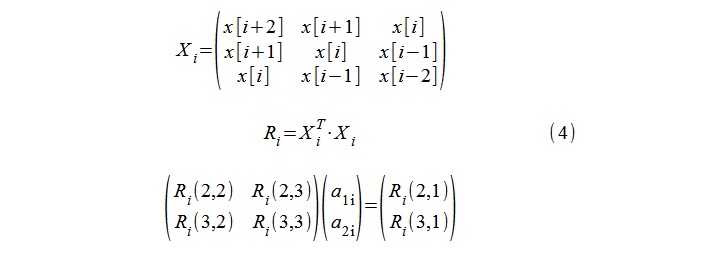
“Полюса“ модели λi затем легко вычисляются логарифмированием корней квадратного уравнения(5).
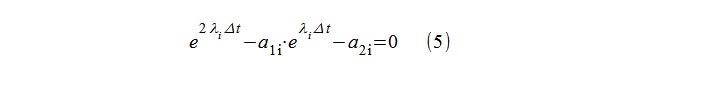
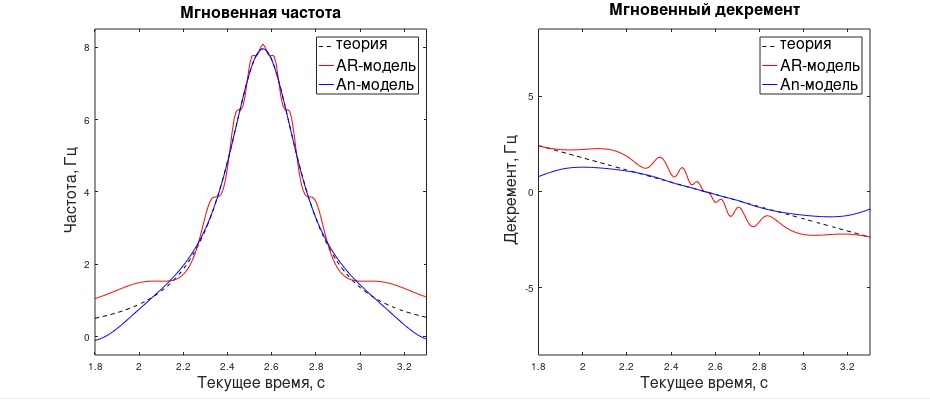
Построение спектральных оценок по известным «полюсам» с точностью до масштабного множителя не представляет сложности. Далее. «Мгновенная мощность» для An-модели определяется очевидным образом, как |y[i]|2, и вопрос масштабирования этой оценки, по-видимому, исчерпан. Для AR-модели обычная техника, связанная с определением мощности условного белого шума, в случае нестационарного сигнала «не работает». За неимением лучших идей, применено масштабирование, исходя из среднего квадрата по соответствующим 5 отсчетам. Похоже, ничего большего, анализируя только 5-сэмпловую последовательность, сделать нельзя. На анимации видно, как AR-график СПМ иногда ощутимо «проваливается» относительно An-оценки. Надо понимать, моменты перехода «через ноль» для AR- модели могут представлять сложности не только в плане погрешностей с мгновенной частотой, но и с мгновенной амплитудой, особенно в области низких частот.
Несколько замечаний напоследок.
- По имеющемуся опыту, оба метода обычно дают хорошие результаты оценки мгновенной частоты, по крайней мере, в среднем (исходя из частоты дискретизации) частотном диапазоне.
- Сравнительно высокое качество результатов An-метода, его простота и легкость в понимании и реализации с лихвой «компенсируются» возможными трудностями с преобразованием процесса по Гилберту. Цифровой фильтр Гилберта надлежащего качества, особенно в широком частотном диапазоне, может иметь неприемлемо высокий порядок. При реализации альтернативного периодограммного метода этого преобразования необходимо учитывать, что преобразование Фурье неявно подразумевает достраивание процесса до периодического. Как следствие, может потребоваться явное значительное достраивание процесса нулями. Высокое качество результатов An-метода объясняется использованием им информации по весьма обширной окрестности выбранного момента времени (строго говоря — по всей временной реализации процесса), и это же свойство затрудняет реализацию метода (например, при работе в реальном времени).
- В случае необходимости для улучшения результатов AR-метода можно рекомендовать следующие меры:
- Прореживание данных (при чрезмерно высокой частоте дискретизации)
- Увеличение числа осреднений — расширение вовлекаемой в модель окрестности «момента времени» — построение трековой матрицы X с большим количеством строк.
- Увеличение порядка AR-модели.
Автор: crowncork




