Объяснение физической сущности явления «Подъёмная сила Крыла» без использования уравнения Бернулли

Монин Илья Алексеевич, к.т.н. СМ-9, 926-220-95-74, imoninpgd@gmail.com

Критика существующего Теоретического объяснения Подъёмной Силы на крыле самолёта

Прослушав курс лекций МФТИ Факультет аэромеханики и летательной техники (ФАЛТ) «Введение в Аэродинамику» и прочитав несколько разных ВУЗовских учеников по «Аэродинамике» [1-3], я был озадачен рядом явных противоречий в объяснениях физики процесса обтекания потоком воздуха (газа или идеальной жидкости) различных твёрдых предметов и формирования подъёмной силы на крыле.

1. Основной тиражируемой Версией образования подъёмной силы на крыле заявляется разность скоростей течения воздуха (жидкости) над крылом и под крылом, и вследствие этого возникает перепад давления согласно Закону Бернулли. При этом однозначно связывают через закон Бернулли расчётную скорость потока на поверхности крыла с инструментально регистрируемым давлением на крыло, игнорируя другие возможные объяснения на основе не менее базовых законов физики.
2. При анализе обтекания идеальной невязкой жидкостью профилей в плоских течениях удивительным образом получали кратное повышение скоростей потока в сравнение с базовой скоростью V0. То есть опровергается закон сохранения энергии, так как энергия на разгон потока берётся ниоткуда, кратно превышая энергию набегающего на крыло потока. При этом игнорируется постулат гидродинамики, что по тому же закону Бернулли при истечении струи из-под уровня скоростной напор однозначно ограничивается сверху статическим напором в сосуде, то есть скоростной напор струи после разгона на крыле не может превысить статического давление сжатой при торможении среды.

Для полёта современного самолёта необходимая подъёмная сила в 500-600кг/м.кв. При совершении взлёта-посадки скорости современных самолётов составляют около 250км/ч. В этом случае нужная подъёмная сила на крыле обеспечивается при скорости обтекания верхней плоскости порядка 450км/ч.

Каков механизм такого разгона потока воздуха без видимого механизма разгонного воздействия на него?

Ведь контакт крыла с набегающим потоком может вести только к торможению потока, но никак не к его разгону!

Эти противоречия необходимо снять!

Физика не должна терять Физический смысл в угоду красивым и сложным математическим построениям!

Рассмотрим иное объяснение формирования подъёмной силы крыла без выявленных нарушений законов физики и здравого смысла. Для этого потребуются применение законов обычной механики.

В рассмотрении считаем, что воздух состоит из отдельных взаимно отталкивающихся (для создания давления газа) частиц с собственной массой, каждая из которых подчиняется законам механики при изменении её направления и величины скорости движения.

Неоднозначность связи разрежения над крылом с повышенной скоростью потока

Рассматриваемое реальное крыло не является элементом идеальной трубки в модели Закона Бернулли, а является ограниченным твёрдым объектом в неограниченном пространстве движущегося реального газа, состоящего из вполне осязаемых по массе и размеру частиц газа. В таком случае следует рассмотреть криволинейное течение струй над криволинейной поверхностью крыла с учётом сил инерции и создаваемого давления, перпендикулярного вектору скорости и поверхности крыла.

Если рассматривать движение струй над профилем крыла, то создать разряжение над крылом может струя воздуха за счёт криволинейности своего течения.

Так для искривления прямолинейного движения тела нужно приложить силу, в перпендикулярном к вектору скорости направлении. В случае непрерывной плоской струи для её искривления нужно обеспечить разность давлений над и под ней. При этом со стороны выпуклости струи будет повышенное давлении, а с вогнутой стороны- пониженное давление.
При движении по окружности материальной точки центростремительное ускорение будет создаваться силой

F=m*V^2/R

А при таком же круговом движении тонкого слоя газа толщиной dR масса будет равна

m= q*S*dR,

где S- площадь участка слоя газа, q- плотность газа. Если привести центростремительную силу к элементарной площадке слоя газа, сила превратится в давление

P=q*V^2*dR/R

При протекании воздушной струи по поверхности крыла слой газа движется по криволинейной траектории. В каждой точке этой траектории существует свой радиус кривизны, который позволяет посчитать ИНЕРЦИОННОЕ давление газа в перпендикулярном к скорости направлении.

Таким образом, можно напрямую посчитать давление (разряжение) на крыле от слоя текущего над его поверхностью газа, при этом скорость течения газа будем всегда считать равной скорости полёта крыла Vo.

Для начала рассмотрим простейший случай крыла в виде изогнутой с радиусом R пластиной нулевой толщины. Такие тонкие изогнутые профили используют для сверхлёгких планеров в авиамоделизме.

Кстати, по привычной теории с законом Бернулли у тонкой изогнутой пластины вообще не должно быть подъёмной силы, так как длина пути под крылом и над крылом одинакова. Но подъёмная сила у тонкого крыла есть, причём весьма значительная, что однозначно показывает неправильность модели подъёмной силы с применением закона Бернулли.

Для оценочного расчёта крыла выберем привычную для малоскоростных самолётов высоту профиля 20% от ширины крыла. В данном случае за высоту профиля примем разницу высот передней и задней кромки по отношению к горизонтальному воздушному потоку (см.рис.1-3)

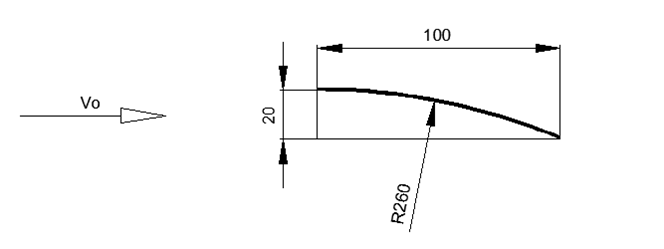
Рис.1. Геометрия тонкого крыла постоянной кривизны

Рис.2. Предполагаемый режим обтекания тонкого радиусного крыла

Рис.3. Характер распределения давления по тонкому радиусному крылу и равнодействующие силы по направлениям

Тогда при ширине 1м и 20% высоте профиля радиус крыла составит 2,6м, при условии горизонтального расположения касательной к крылу в верхней точке профиля.

Теперь рассчитаем центростремительное давление на крыло от искривлённого по дуге слоя воздуха.

Так для скорости 70м/с (252км/ч) давление одного слоя толщиной 0,1м с радиусом кривизны 2,6м составляет 235,6Па или 24кг/м.кв., а величина скоростного напора при 70м/с равна 3063 Па.

Если учесть, что у тонкого крыла обтекание происходит с двух сторон, то эти величины нужно как минимум удвоить, а затем ещё и умножить на некоторое количество параллельных слоёв, так же искривлённых двигающимся крылом. Если предполагаем, что толщина возмущённого слоя не менее половины ширины крыла с каждой стороны крыла, то получаем суммарную удесятерённую нагрузку на крыло около 2356 Па. Эти цифры прекрасно бьются со значениями нагрузок на крыло для низкоскоростных лёгкомоторных самолётов с толстым крылом и аналогичной кривизной поверхности крыла. (см.таб.1)

Так как давление Ркр приложено к криволинейной поверхности тонкой пластины, то сила Fкр от Ркр может быть разложена на Подъёмную силы Fy и на силу Сопротивления полёту Fх.
Подъёмная сила Fy равна интегралу проекции на ось Y сил от Давления Криволинейного потока Ркр по всей площади крыла.

В случае равномерного давления на круговое крыло величина Fy будет равна произведению Ркр на площадь проекции крыла на ось Х, что равно S=B*L крыла ( в данном случае 1м.кв/м.п.).

Fy=Ркр*Bкр= 2356*1=2356 Н/м.п.

В то же время сопротивление горизонтальному движению в этом случае будет равно интегралу проекции dFкр на ось Х по всей площади крыла. В случае равномерного давления на крыло величина Fx будет равна произведению Ркр на площадь проекции крыла на ось Y, что равно высоте Н профиля крыла ( в данном случае 0,2м.кв/м.п.).

Fx=Ркр*Нкр= 2356*0,2=462 Н/м.п.

При этом получим К= Fy/ Fx= (Ркр*Bкр)/ ( Ркр*Нкр ) = Bкр/ Нкр, то есть при равномерном давлении на круговом тонком профиле качество крыла равно отношению только геометрических параметров профиля К=В/Н.

Согласно правилу векторного разложения сил из заданной картинки можно сразу получить величину качества крыла К=Fy/Fx, что в данном случае равно К=100*Ркр/20*Ркр =5.

Интересно, что если отмасштабировать данное расчётное крыло в сторону десятикратного уменьшения (по радиусу кривизны, высоте и ширине профиля), то давления на крыло при этом останутся неизменными при равных скоростях полёта (см.таб.2). Именно по этой причине тяжёлые крылатые ракеты летят на достаточно маленьких тонких крылышках. Оказывается, что их небольших по площади и тонких крыльев при достаточной кривизне действительно хватает для создания необходимой подъёмной силы!

Так как комнатный моделизм достаточно дёшев, то эти цифры достаточно просто проверяются на натурных моделях.

Таб.1. Давления искривлённых слоёв воздуха на крыло постоянного радиуса R=2,6 м в зависимости от скорости полёта.

Таб.2. Давления искривлённых слоёв воздуха на крыло постоянного радиуса R=0,26 м в зависимости от скорости полёта.

Интересно рассмотреть, как меняется Ккр крыла при постоянной его кривизне Rкр, но при изменяющемся параметре ширины профиля Вкр. (См.таб.3)

В самой первой строчке таблицы аэродинамическое качество крыла достигает фантастического значения К=182, но при этом нагрузка на крыло составляет всего 67Па (7кгс/м.кв), что пригодно только для авиамоделей планеров комнатной размерности.

Необходимая подъёмная сила на крыле возникает только при достаточно малых К крыла, что видно по последним строчкам таблицы.

Жёлтым выделены столбец изменяемого параметра и строчка исходного профиля с Ккр=5.

Таб.3. Изменение параметров крыла постоянного радиуса R=2,6м при различных углах профиля (ширина профиля) на постоянной скорости полёта.

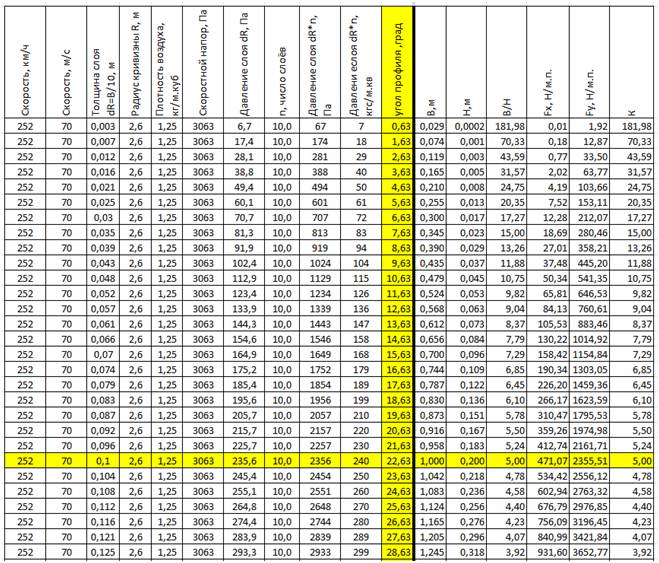
Также можно рассчитать изменение подъёмной силы Fy и качества крыла Ккр для крыла с постоянной хордой, но разной кривизной крыла при постоянной скорости. Жёлтым выделены столбцы: Изменяемый аргумент Rкр- радиус кривизны и постоянная ширина профиля Вкр. Так же выделена строчка исходного профиля с Ккр=5.

Таб.4. Изменение параметров крыла переменного радиуса кривизны при постоянной ширине профиля В=1м на постоянной скорости полёта.

В описанной модели для получения разряжения над крылом не требуется дополнительный разгон воздуха над крылом. Заметное разряжение над крылом обеспечивается в условиях значительного искривления обтекающего крыло потока воздуха под действием статических сил давления воздуха всего окружающего пространства. Угол наклона хорды исходной изогнутой пластины составляет 11,3 градуса (половина угла сегмента дуги в 22,6град), что хорошо согласуется с посадочными режимами работы крыла современных авиалайнеров при посадке с выпущенной механизацией крыла (предкрылки +закрылки). В посадочном режиме крыло с выпущенной механизацией намного больше напоминает рассмотренный случай изогнутой тонкой пластинки, чем классическое крыло с прямой нижней плоскостью (см.рис 4).

Рис.4. Крыло несимметричного профиля с плоской нижней обтекаемой поверхностью: а) выпрямленное положение для скоростного полёта; б) крыло с максимальной кривизной при полностью выпущенной механизацией.

Сильно изогнутое тонкое крыло широко применяется в качестве лопастей вентиляторов. Низкие линейные скорости при малых величинах давления позволяют использовать в вентиляторах в качестве лопастей тонкие стальные или пластиковые пластины крайне малой толщины, так как их прочности хватает для выдерживания имеющихся нагрузок.

У тяжёлых самолётов использование тонких крыльев технически невозможно по причине их недостаточной прочности. Большая толщина крыла позволяет разместить внутри крыла достаточно высокие несущие балки достаточной прочности и жёсткости на изгиб и кручение, при этом сохранив приемлемый для самолёта вес. Именно по этой причине вся аэродинамика изучает крылья со вполне осязаемой толщиной. По этой причине переходим от рассмотрения аэродинамики тонкой изогнутой пластины к профилю крыла с реальной толщиной и плоскостями различной кривизны.

В завершении рассмотрения модели обтекания тонкого крыла необходимо привести ещё одно доказательство работоспособности предложенной модели объяснения «Подъёмной силы крыла». Как известно из механики, Сила- это изменение импульса в единицу времени, то есть

F=d (m*V)/dT

В озвученной модели обтекания тонкого криволинейного крыла мы можем подсчитать подъёмную силу Fy как изменение импульса набегающего потока воздуха по вертикали, который считается как

Fy2= (dR*10*q*Vo)*Vo*sinАкр,

Где Vo-скорость крыла, dR –толщина элементарного искривляемого слоя потока воздуха в расчётной модели, 10- число искривляемых одновременно слоёв, Акр- угол схода потока с крыла к направлению исходной скорости Vo.

Проведя расчёт получим, что оба расчёта дают одинаковый результат.

Или в аналитическом виде:

Fy1=Ркр*Bкр,

Ркр= (dR*10*q*Vo)* Vo/R,

Bкр=R* sinАкр

Подставив развёртки Ркр и Bкр в выражение для Fy1 и сократив одноимённые R в числителе и знаменателе, получим:

Fy= Ркр*Bкр= (dR*10*q*Vo)*Vo*sinАкр

А значит всегда верно равенство Fy =Fy1= Fy2

То есть «Инерционно-криволинейный» метод расчёта «Подъёмной Силы» крыла даёт формулу идентичную с методом «Реактивно-Импульсной Силы» для крыла одинаковой геометрии.
Это значит, что самолёты летают не благодаря какой-то «магической» силе из «магических вихрей», а благодаря старому и понятному «Импульсу Силы» или «Реактивной тяге» при отбрасывании массы воздуха вниз.

Толстое Крыло

На малых скоростях полёта при взлёте-посадке (М= 0,2 или 250км/ч) скоростной напор не превышает 3кПа (3% от Атмосферного давления на уровне моря в 100кПа), то есть он столь мал по отношению к базовому атмосферному давлению, что геометрическое сжатие потока становится визуально не обнаружимо при рисовании струйного течения у крыла.

Для создания подъёмной силы над крылом необходимо создать искривление потока так, чтобы крыло находилось в зоне вогнутости потока воздуха. Обеспечить такое искривление струи над крылом помогает кривизна верхней плоскости крыла, находящейся в аэродинамической тени носового обтекателя крыла.

При этом нижняя плоскость крыла обтекается либо по прямой, не создавая разряжения, или по вогнутой поверхности, отбрасывая поток воздуха вниз, что создаёт уже положительный прирост давления на крыле снизу и суммируется с подъёмной силой от разряжения над крылом.
Главным отличием толстого крыла от тонкой пластины в нашем случае будет появление лобового обтекателя, раздвигающего встречный поток воздуха до того, как он достигнет изогнутых плоскостей, создающих подъёмную силу.

Перед летящим толстым крылом возникает зона торможения, где скорость движения воздуха становится равной нулю (относительно крыла), а избыточное давление в этой зоне равно скоростному напору Рvo.

Нарисовать линии тока без учёта сжатия воздуха не получится, иначе придется либо принять версию об ускорении воздуха над поверхностью крыла, либо зона влияния с искривлением потока устремится к бесконечности в несжимаемой среде, что является неправдоподобным.
Кстати, оба эффекта (Ускорение потока и Бесконечная зона влияния в несжимаемых жидкостях) проявляются на практике в аэродинамических трубах с дымовыми линиями тока и при движении подводных лодок на малых глубинах.

Так в аэродинамических трубах (АДТ) обтекание тестируемых макетов происходит с заметным ускорением потока (уменьшение толщин дымовых линий ) в зазоре стенка АДТ-макет. Вот только толкование этого явления совершенно неверно относят к ускорению потока для формирования подъёмной силы. В действительности ускорение потока в зазоре «стенка АДТ-макет» является просто следствием заужения проходного сечения в проточном тракте АДТ при сохранении постоянного расхода воздуха в самой АДТ за счёт мощных вентиляторов с жёсткой вентиляторной характеристикой.

При движении подводных лодок на малых глубинах над подводной лодкой образуется Визуально Заметный водяной горб. Величина этого горба равна объёму воды перед корпусом подлодки, который надо как-то переместить из зоны перед подлодкой в зону кормы при движении с заданной скоростью. Горб на поверхности образуется и при движении подлодки на больших глубинах, но из-за большей площади растекания горба его высота становится необнаружимой при простом визуальном наблюдении. Причиной возникновения горба воды на поверхности объясняется невозможностью переместить несжимаемую жидкость в сторону дна, а в сторону поверхности тонкий слой воды под атмосферным давлением воздуха становится Легко Сдвигаемым, с понятной упругой характеристикой пружины Атмосферного давления и Сил Тяготения. Кстати, даже при движении подводных лодок на больших глубинах водяной горб (и саму подлодку как следствие) могут обнаружить при наблюдении со спутников с помощью высокочувствительной аппаратуры, способной замерять геометрию поверхности морей с большой точностью и вычленить горб воды от подлодки из шума волн на поверхности с помощью ЭВМ.

Таким образом, принимаем газ сжимаемым, а зону влияния от огибания крыла ставим в зависимость от величины сжатия струи от давления Рvo.

Давление в зоне торможения у обтекателя удерживается искривлёнными струями воздуха, огибающими обтекатель. Связь давления с искривлением слоёв воздуха такая же, как и в случае с тонким изогнутым крылом dP=q*Vo^2*dR/Rсл.

Величина зоны влияния, где заметно искривление потока, также связано с величиной Вкр и Нкр. Повышение давления перед обтекателем будет скомпенсировано понижением давления в спутной струе позади крыла, то есть крыло формирует линейный Диполь по давлению, который на большом удалении практически перестаёт влиять на окружающее воздушное пространство на малых (дозвуковых) скоростях полёта.

Если принять форму носового обтекателя круглой, то половина высоты профиля будет равна Нкр/2=Rлоб.

Считаем, что зона торможения с давлением Рvo целиком создаётся кривизной слоя в границах ширины профиля Вкр, тогда можем оценить радиус кривизны струи толщиной Нкр/2= Rлоб.
Необходимо выполнить условие Pr= Рvo.

Следовательно

qVo^2*Rлоб/R= qVo^2/2

После сокращения одинаковых членов плотности и скорости соответственно в левой и правой части уравнения получаем

R= 2* Rлоб

Таким образом, получается, что предельные радиусы кривизны набегающего потока ограничены исключительно кривизной обтекателя (локальной высотой профиля), и при этом не зависят от скорости.

При повороте набегающей струи в обход профиля неизбежно возникает ситуация, в которой граничная с нулевой линей потока струя касается обтекателя. В этой точке касания скорость потока направляется от крыла, а кривая потока достигает точки перегиба. То есть в этой точке происходит отрыв слоя от крыла с изменением направления выпуклости кривизны струи (см.рис.5).

Рис.5. Взаимодействие набегающего потока Vo с лобовым обтекателем крыла.

На больших скоростях полёта величина скоростного напора Pvo столь велика, что струя отрывается от носового обтекателя и, описав длинную дугу над плоскостью крыла, возвращается обратно к поверхности крыла.

В месте возврата оторванной струи на плоскость крыла возникает Удар, а струя скачком меняет направление на касательное к плоскости крыла. При этом под дугой летящей струи от точки отрыва до точки возврата возникает замкнутая полость низкого давления. (см.рис.6).

В традиционной «Бернуллиевской Аэродинамике» описанное образование развитого отрывного пузыря с сильным разряжением и ударный возврат отрывной струи объясняют так: « …На высоких предзвуковых и трансзвуковых скоростях возникает ускорение потока воздуха над крылом до сверхзвуковых значений, в результате чего давление над крылом сильно снижается, а потом возникает скачёк давления (удар перехода на сверхзвук), с переходом после него на дозвуковое течение…». Такое объяснение выглядит как явная натяжка реальных экспериментальных данных на несостоятельную теорию.

Так как обтекатель делит набегающий поток на две части по нулевой линии, то отрыв потока возникает на обеих плоскостях крыла. Но из-за различных направлений плоскостей по отношению к потоку (на поток или в аэродинамической тени) отрывные пузыри разряжения над и под крылом имеют разный размер, и так же изменяется сила удара возвратной струи, пропорционально размеру отрывного пузыря.

На основе такого распределения эпюр давления на переднем обтекателе крыла и полученых качеств Ккр тонких радиусных пластин-крыльев в зависимости от относительной толщины профиля Вкр./Нкр. легко можно понять причины и закономерности такого явления, как «Обтекаемость» различных геометрических форм (см.Эпюру Сх на рис.6).

Так же было бы крайне интересно рассмотреть эпюры давления при Обтекании струйными течениями стандартных осесимметричных тел и получить их равёртки Сх и Су по сечениям, а не только один суммарный коэффициент Сх для фигуры в целом.

Рис.6. Обтекание струями воздуха толстого крыла с обозначенными характерными элементами движения. Эпюра давлений на крыло и диаграммы коэффициента давления Су по хорде крыла и Сх по высоте крыла. Площадь закрашенных зон соответствуют суммарным силам по направлениям Y и Х соответственно.

При низких числах М основная подъёмная сила формируется в зоне носового обтекателя в отрывных пузырях. При малых числах М возвратная струя в зоне отрыва идёт по касательной к толстому профилю крыла и не вызывает Удара в точке возврата. Но при приближении к М=1 отрывные пузыри раздуваются на столько сильно, что становится невозможно добиться нужной толщины профиля для безотрывного течения струи, и тогда возникает выраженный Отрыв потока с образованием Отрывного Пузыря, визуально наблюдаемого по колебаниям шелковинок, наклеенных на плоскость крыла. Раздувание отрывных пузырей по высоте становится препятствием для набора скорости, и потому их развитие начинают уменьшать за счёт заострения носовой кромки (понижение радиуса лобового обтекателя).
При трансзвуковых скоростях полёта задняя граница отрывного пузыря достигает задней кромки крыла, после чего происходит соединение объёмов верхнего отрывного пузыря с зоной высокого давления нижней плоскости крыла. В объединившихся объёмах верхнего и нижнего отрывных пузырей давление выравнивается, а подъёмная сила крыла Fy резко падает.

При сверхзвуковом полёте крыло привычной каплевидной формы становится уже совсем неприменимым, а вместо этого появляется крыло с развитым острым «клювом», на котором теперь и создаётся основная часть подъёмной силы, при этом минимизируется возможность возникновения отрывного пузыря.

Для обеспечения посадочных режимов полёта на низких числах Маха в «тонкоклювое» крыло осуществляют установку передней и задней отклоняемой механизации (см.рис.7). Подобного типа тонкие крылья с острыми передними кромками и отклоняемой передней и задней механизацией ставят на боевые истребители 4-5 поколений (см.фото.1-2). При отклонения механизации вниз «тонкоклювое» крыло становится близко к характеристикам обтекания тонкой изогнутой пластины, что позволяет осуществлять взлёт и посадку на малых скоростях и с коротким пробегом по ВПП. В перспективе возможен переход на поворот плоскости крыла целиком при выполнении манёвров на малых скоростях, как это уже сделано с полностью поворотным хвостовым оперением истребителей. Полностью поворотная плоскость крыла позволит избегать сильного задирания фюзеляжа против потока воздуха и сохранения сонаправленности вектора тяги двигателей к скорости полёта на больших углах атаки.

Рис.7. Профиль тонкого крыла Н/В=0,1 (10%) с острым отклоняемым «Клювом» и широким отклоняемым закрылком: а) выпрямленное положение для сверхзвукового полёта; б) отклонение механизации вниз для полётов на малых скоростях и в посадочном режиме с большими углами атаки.

Фото.1. Су- 35 на большом угле атаки с отклонёнными предкрылками и закрылками в посадочном режиме (выпущены шасси).

Фото.2. МиГ-29 с отклонёнными предкрылками и закрылками во взлёт-посадочном режиме на большом угле атаки и низкой скорости (выпущены шасси).

Фото.3. МиГ-29 на взлёте с полным отклонением вниз передней и задней механизации крыла.

На фото (см.фото.3) хорошо видна форма «остроклювого» предкрылка в сечении: плоская нижняя грань и радиусная верхняя грань. Сама передняя кромка отнюдь не острая, а имеет весьма конкретный малый радиус, тем самым улучшая аэродинамику дозвукового полёта. Управление наклоном предкрылка к набегающему потоку позволяет оптимизировать режим образования отрывного пузыря на низких скоростях, создав условия для его безотрывного схлопывания. Так же, учитывая фигуры высшего пилотажа с возможностью длительного полёта вверх ногами, отклоняемый вверх предкрылок позволяет сделать обратный прогиб плоского тонкого крыла для вполне эффективного полёта в перевёрнутом положении, хотя и с худшей аэродинамикой, чем в нормальном положении. На более поздних самолётах Су-35 и Су-57 передняя кромка острее и более симметрично клиновидная, так как рассчитана на более длительный сверхзвуковой полёт.

Вихреобразование и вихревое сопротивление крыла

В сети можно найти массу объяснительного материала по любому вопросу, в том числе и к Вихреобразованию на крыле самолёта, например такой:

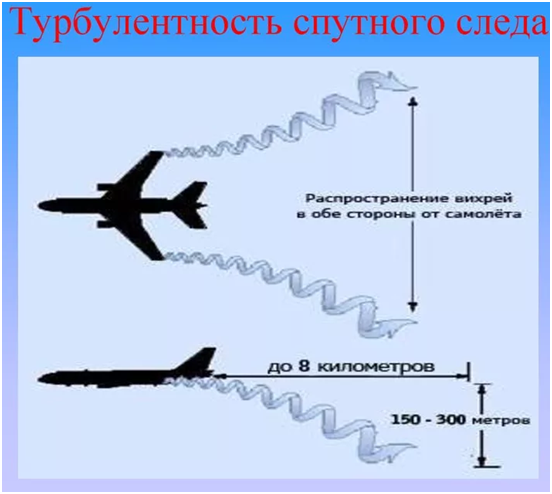
В тоже время в том же интернете легко найти Фотографии вихревых следов от самолётов в облачных слоях, которые демонстрируют гораздо больший масштаб явления, чем это нам пытаются показать в теории.

Фото.4. Вихревой след в слое тумана за летящим на высоте самолётом. Кольца видимого туманного вихря отстоят от самолёта на сотни метров, а визуальная близость – это оптическая иллюзия, созданная длиннофокусным телеобъективом при съёмке самолёта с дистанции в несколько километров.

Фото.5. Вихревой след в слое тумана за летящим на высоте самолётом. Виден вертикальный поток воздуха и заходящие с боков волны воздуха, закручиваемые в спираль при соприкосновении с вертикальным нисходящим потоком.

Фото.6. Вихревой след в слое тумана над ВПП за приземляющимся самолётом.

Эти огромные спутные вихри за самолётами формируются вовсе не за счёт концевых вихрей на крыле. Концевые вихри существуют, конечно, но их роль не так велика и с ним активно и успешно борются конструкторы самолётов.

Крупномасштабные вихри с фотографий формируются уже далеко за самолётом, когда волна воздуха, отброшенная самолётом вниз, замещается с двух боковых сторон перетоком воздуха из-под нисходящего слоя в разреженное пространство сверху (см.фото.4-5). Это объяснение образования спутного вихря перекликается с уже рассмотренным вопросом «зоны влияния крыла на окружающее пространство». При этом роль земной поверхности заключается в Границе распространения вниз отброшенного крылом вниз потока воздуха. То есть полёт самолёта и создание «подъёмной силы крыла» возможен и при отсутствии твёрдых подстилающих поверхностей, но при этом отброшенный вниз поток воздуха будет бесконечно долго двигаться вниз, по мере удаления теряя скорость и кинетическую энергию, но сохраняя неизменным вертикальный импульс. Кинетическая энергия первоначальной отброшенной массы воздуха будет теряться на вовлечение в движение боковых потоков воздуха, симметричная разнонаправленность которых не будет изменять исходный суммарный импульс, созданный крылом самолёта. Наглядной иллюстрацией роли Земли-Ограничителя является Фото.6. Там прямолинейный ток тумана над садящимся аэробусом (см.фото.6) опускается до земли по прямой и только потом далеко за самолётом начинается сдвиг в стороны вдоль земли-ограничителя, а слои тумана с боков и сверху уже надвигаются в середину спутного слоя, закручиваясь в двойную самокомпенсирующуюся спираль о нисходящий поток.

«Экранный Эффект» при полёте крыла вблизи Земли

В свете изложенной роли Земли при формировании «Подъёмной силы крыла» имеет смысл дополнительно рассмотреть «Экранный Эффект», который без наличия твёрдой земной поверхности не может возникнуть. Таким образом, физика Полёта крыла в Бескрайнем воздушном пространстве и на «Экранном Эффекте» вблизи Земли имеет весьма различную природу.

Объяснения эффекта «Экраноплана» исходя из сжимаемости газа при малых числах Маха

Влияние близко расположенной поверхности земли на подъёмную силу крыла называют «экранным эффектом». При этом эффекте резко повышается подъёмная сила крыла при полёте вблизи твёрдой поверхности (земля, вода) на высоте сопоставимой с величиной хорды крыла. Основываясь на этом эффекте даже появился целый класс низко летающих аппаратов- «Экранопланов».

В чём же суть явления? Разобраться с этим вопросом можно только предположив, что воздух является Сжимаемым газом.

Тогда при полёте крыла над поверхностью земли образуется воздушный зазор ограниченного размера между двумя твёрдыми поверхностями. При полёте крыла с небольшим положительным углом атаки встречный поток воздуха под крылом испытывает постепенное сжатие от передней кромки крыла к задней кромке (см.рис.8).

Максимальное давление сжатия об экран потока под крылом зависит только от скоростного напора относительно летящего крыла, и это давление в сжатом слое не может превысить давление скоростного напора воздуха:

Ро=Vо^2*Q/2,

где Ро- скоростной напор воздуха при скорости крыла Vо, Vо-скорость полёта крыла, Q-плотность воздуха.

Зная максимальное приращение давления под крылом, рассчитаем геометрические параметры в зазоре «воздушной подушки».

Так при скорости 40 м/с (144км/ч) скоростной напор Ро= 1кПа или 1% от 1атм. (100кПа).
То есть на скорости 40 м/с максимальное давление под крылом достигается при сжатии на 1% по высоте Х зазора от передней кромки крыла к задней. На глаз такое поджатие практически необнаружимо, а слой под крылом визуально кажется плоским (см.рис.8.а).

При этом угол атаки составит А=(Ро/Ратм)*Х/В радиан (при малых углах sinA=A),
где В- хорда крыла, Х- величина воздушного зазора до земли под крылом на уровне задней кромки крыла, Ро- скоростной напор воздуха при скорости крыла Vо, Ратм- атмосферное давление (на уровне моря Ратм= 100кПа).

Получается, что максимально эффективный угол атаки для получения экранного эффекта зависит от высоты полёта крыла над поверхностью, конструктивной ширины крыла и заданной скорости полёта, а угол атаки оказывается лишь производной этих величин.

Вывод: Можно почти бесконечно наращивать ширину крыла, сводя угол атаки почти к нулю, тем самым достигая минимального сопротивления Сх при практически обнуленной индуктивной составляющей сопротивления.

«Экранный эффект» на низких скоростях полёта обеспечивает очень высокое качество крыла, так как создаёт максимальную удельную подъёмную силу на крыле, равную скоростному напору Ро при крайне малых углах атаки на практически плоском и очень тонком крыле. Качество крыла на малых числах Маха при полёте на экране может достигать величины К=25-30.
Вклад разрежения над верхней выпуклой поверхностью крыла при таком полёте на «экране» с плоским крылом достаточно мал в сравнении с давлением под крылом.

При повышении скорости полёта скоростной напор растёт квадратично, а для получение максимального экранного эффекта приходится задирать угол атаки пропорционально росту скоростного напора Ро.

То есть наращивание скорости Vо с целью увеличения Ро влечёт Квадратичное к росту скорости увеличение Угла атаки, что в свою очередь резко снижает качество крыла. И начиная с некоторой скорости Vо-max величина экранного эффект с большим углом атаки сравнивается с подъёмной силой обычного авиалайнера в посадочном режиме с выдвинутой механизацией крыла.

Для любого крыла с хордой В для увеличения высоты полёта Х необходимо задирать угол атаки, после чего Экраноплан поднимется на некоторую новую высоту Х2, где опять установится баланс степени поджатия струи за счёт нового угла атаки на новой высоте. При этом с увеличением высоты полёт экраноплана начинает линейно возрастать сопротивление полёту и соответственная ему потребная сила тяги тоже возрастает без изменения скорости полёта. То есть топливная экономичность полёта экраноплана может разительно изменяться от подъёма по высоте всего на несколько метров.

Рис.8. Конфигурация воздушных потоков на «Экранном эффекте»: а.) Оптимальный угол атаки без застойной зоны под крылом, б.) Избыточный угол атаки, формирующий большой пузырь застойного воздуха повышенного давления между крылом и поджатым слоем воздуха «Экранной воздушной подушки».

Вывод: Дополнительное задирание угла атаки крыла без увеличения скорости полёта на экране не даёт приращения подъёмной силы, а лишь увеличивает сопротивление полёту Сх (см.рис.8.б)

Считая угол хорды крыла авиалайнера в посадочном режиме около 15 градусов можем оценить величину сжатия струи под крылом до давления Ро и соответствующей ему скорости Vо, считая при этом величину хорды В равной высоте полёта крыла Х.

15 градусов соответствует sin15= 0,262

При угле атаки 15 градусов должен быть скоростной напор Ро=0,26атм= 26кПа, но такие давления реализуются на очень высоких скоростях (740км/ч) и намного превосходят необходимые для полёта расчётные нагрузки на крыло. То есть такой большой Посадочный угол атаки для создания экранного эффекта над ВПП является избыточным на посадочных скоростях 250-300 км/ч.

Качество крыла при угле атаки 15 градусов упадёт до величины всего К=3,7.
Посадочная скорость авиалайнера всего около 250км/ч (70м/с), при этом скоростной напор составит Ро=3кПа или всего 3% от Ратм, тогда как нормальна расчётная нагрузка на крыле в полёте составляет 5кПа (500кг/м.кв=5% от Ратм). То есть при посадке экранный эффект у авиалайнера начинает заметно ощущаться пилотом на высоте соизмеримой с шириной крыла В, сопоставимой с высотой стоек шасси. Выравнивание самолёта и снижение угла атаки для скорости 250км/ч позволяет самолёту пробить «экранную воздушную подушку», так как её несущая способность оказывается ниже, чем потребное давление под крылом для полёта.
За счёт «Экранного эффекта» возникает «Несажаемость» у самолёта в горизонтальном полёте без выпуска механизации крыла при угле атаки 5% (или 3 град.) при скоростном напоре Ро=5кПа, что соответствует Vо=324км/ч или 90м/с.

Угол атаки 5% (или 3 град.) создаёт качество крыла экраноплана равное К=20.
Высокий К=30 соответствует углу атаки в 3% (2 град), при этом подпор под крылом составит всего 3% * Ратм = 3кПа (300кг/м.кв), что соответствует скоростному напору при Vо=70м/с (250 км/ч).

Таким образом, экономически эффективные режимы полёта в режиме «экраноплана» в сравнении с обычным высотным «самолётом» лежат в зоне малых скоростей. При падении качества крыла экраноплана ниже К=20 выгоднее использовать для транспортировки обычный высотный самолёты. То есть экономически выгодные области эксплуатации Экранопланов соответсвуют скоростям ниже 300км/ч.

Маневрирование Экраноплана

Отдельного рассмотрения заслуживает вопрос маневрирования Экраноплана в полёте. Так как подъёмная сила крыла на «экране» формируется иначе, чем при высотном полёте, то и маневрировать «по- самолётному» экраноплан не может.

Экраноплан не может закладывать виражи с креном на крыло, так как он немедленно получит потерю подъёмной силы на задранном крыле и касание воды опущенным крылом. Для экраноплана поворот возможен только «блинчиком», то есть совершенно без крена, а только за счёт создания боковых сил от вертикального оперения.

Само вертикальное оперение Экраноплана тоже должно отличаться от самолётного оперения. Вертикальное оперение Экраноплана должно состоять как минимум из двух килей, способых работать как синхронно, так и вразнобой, что зависит от типа выполняемого манёвра. Вертикальное оперение при этом не только осуществляет разворот Экраноплана вокруг его вертикальной оси, но и создаёт горизонтальную силу поперёк направления скорости полёта.
Горизонтальное оперение на заднем киле выполняет регулирование по углу атаки.
Широкое и короткое крыло необходимо оснащать развитыми концевыми шайбами-скегами, удерживающими спресованый под крылом поток от растекания в стороны. Дополнительно эти шайбы-скеги выполняют роль посадочных понтонов для приводнения.

Также нужно дополнительное горизонтальное оперение на концах основного крыла для компенсации опрокидывающего момента от действия вертикального оперения.

Практически по такой Схеме был построен экраноплан Бериева ВВА-14 (см.рис.9) и многочисленные версии перспективных макетов экранопланов-самолётов, но без переднего вертикального оперения (см.рис.10).

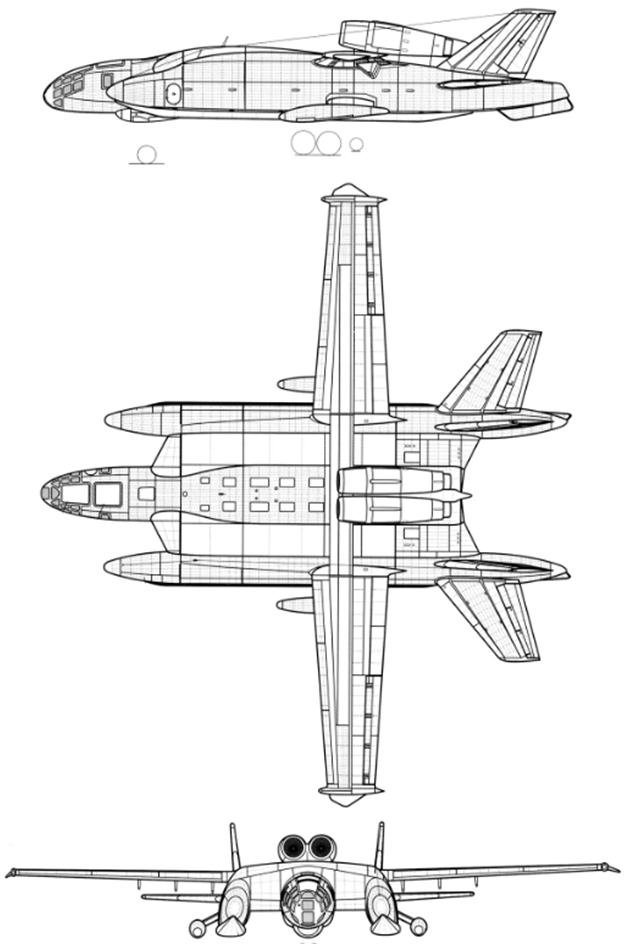
а.

б.

в.

Рис.9 Экраноплан Бериева ВВА-14. а.Чертёж. б. Модель в 3-Д. в. Фото действующего образца на воде.

Рис.10. Макет перспективного большого экраноплана.

Типы манёвров экраноплана за счёт вертикального оперения:

• Два одинаковых разнесённых киля обеспечивают режим «Сдвиг вбок» при синхронном повороте в одну сторону. При этом Экраноплан как бы сдвигается из одной полосы движения в другую без вращения корпуса. При этом горизонтальное оперение работает разнонаправлено, компенсируя кренящий момент от вертикального оперения.
• Если кили повернуть в разные стороны на одинаковый угол, то возникнет поворачивающий момент, вращающий корпус Экраноплана вокруг вертикальной оси. При этом горизонтальное оперение не работает, так как момента от вертикального оперения не возникает.
• Если кили повернуть в разные стороны на разные согласованные углы, то возникнет поворот по круговой траектории (циркуляция), где вектор скорости совпадает с направлением продольной оси фюзеляжа Экраноплана, а сам экраноплан летит по заданной круговой траектории с равными угловыми скоростями полёта и вращения самого экраноплана вокруг вертикальной оси.

  При этом горизонтальное оперение работает разнонаправлено, компенсируя кренящий момент от вертикального оперения.

Все эти режимы практически мало реализуемы в ручном режиме, так как малая высота полёта просто не оставляет времени на реакцию в темпе человеческого восприятия. Для управления Экранопланом нужна автоматизация управлением, подобная автоматической стабилизации сверхнеустойчивых истребителей 4-5 поколения.

Заключение

Все выше сказанные предположения строятся на открыто опубликованных экспериментальных данных (полученные на АДТ эпюры давления на крыле и другие данные).

В экспериментальную Аэродинамику за последний век вбуханы огромные деньги на строительство АДТ различных типов и размеров, так же получен огромный объём фактического материала в экспериментах с макетами различных летательных аппаратов и отдельных элементов крыла.

Вызывает удивление тот факт, что в процессе обучения студентов опираются не на материалы реальных Экспериментов, а на сомнительные теории 100 летней давности. И это при том, что сами экспериментальные данные явно противоречат, этим замшелым Теориям.

Даже в таком обобщённом вводном курсе, как «Введение в Аэродинамику» для ФАЛТ Физтеха, качественные объяснительные модели базового понятия «Подъёмной Силы Крыла» не даются, а вытеснены заумным наукообразным жонглированием математическими формулами (которые к тому же не позволяют ничего рассчитать).

В науке наметился тренд к расколу между теорией и практическим инженерным приложением в разработках конкретных изделий. Явные противоречия в Теоретических моделях не афишируются, а наоборот всячески замалчиваются, дабы не поколебать авторитет замшелых и уже покойных старцев из академии наук и не прервать победного шествия их искренних заблуждений по страницам вполне современных учебников и монографий.

Библиография:

• «Гидравлика и аэродинамика», Альтшуль А.Д., Москва, Стройиздат, 1986.-413с.
• «Аэродинамика» часть 1, Краснов Н.Ф., Москва, Ленанд, 2018,-496с.
• «Аэродинамика», Под ред. Калугина В.Т., Москва, МГТУим.Н.Э.Баумана,2017,-607с.

Автор: iMonin

Источник