Добрый вечер, хабросообщество!
Цель данной статьи рассказать об одном из чудес квантовой информатики, а именно — алгоритм Гровера, который позволяет достичь квадратичное ускорение в сравнении с классическими алгоритмами перебора.
Небольшое знание линейной алгебры желательно.
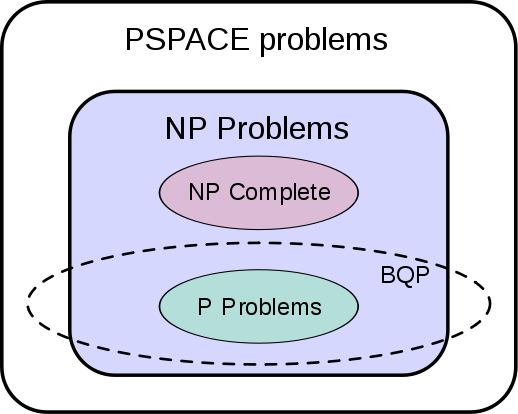
Классический алгоритм перебора
Пусть дана функция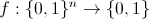 
— булева функция. Цель: найти хотя бы один корень уравнения f(x) = 1. На классическом компьютере, если f — произвольна(например, некоторый черный ящик, оракул), нам понадобиться O(N) операций, где 
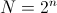, то есть, полный перебор. Если f в конъюнктивой нормальной форме — то данная задача является NP-полной. Проблема о равенстве/неравенстве P и NP является открытой и по сей день.
Квантовый алгоритм
К сожалению, или к счастью, не известен квантовый(а классический тем более) для решения данной задачи за полиномиальное время. Но алгоритм Гровера позволяет получить квадратичное ускорение для полного перебора — за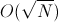 
.
Краткое описание алгоритма
Используя n+1 кубит, мы приготавливаем первые n кубитов в суперпозицию всех возможных состояний, а последний в суперпозицию «нуля» и «единицы», но со «знаком минус» у «единицы». Тогда действуя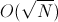 
раз оператором поворота, мы получаем состояние, при измерении которого с очень высокой вероятностью получаем решение уравнения.
Небольшой экскурс в терминологию.
Дираковские обозначения — |x> — обозначает вектор(столбец), а <x| — двойственный к нему вектор(строку). Тогда <x|x> будет скалярным произведением. А |x><x| — будет матрицей, обычное умножение вектор-столбца на вектор-строку.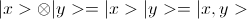 
— обозначает тензорное произведение векторов, чаще записывают кратко: |x,y>.
Пример: |0> и |1> — в двумерном случае обозначают вектора (1,0) и (0,1) соответственно.
|0><0| — матричная единица, где 1 стоит на позиции (1,1).
В двумерном случае: |0><0| =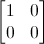 
Суперпозиция — линейная комбинация базисных состояний.
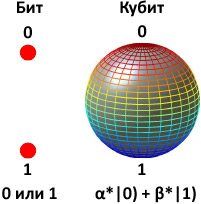
Кубит — наименьший элемент для хранения информации на квантовом компьютере. В отличие от классического бита, который может принимать только 1 и 0, квантовый бит может находится в суперпозиции двух состояний: |0> и |1>, которые «отвечают» за 0 и 1 соответственно.
Элемент Адамара(обозначаемый как H) — действует следующим образом: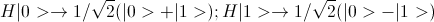 
H =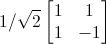 
— матричное представление
Элемент Уолша-Адамара(обозначаемый как WH,W) — Тензорная степень H.
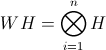
Квантовое состояние системы из n кубитов:
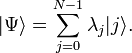, где 
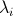— некоторый коэффициент(амплитуда), комплексное число, а 
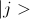— вектор, с единицей на i позиции.
Классическое состоянии системы из n битов будет одним из N вариантов(например, числом от 0 до N-1), то квантовое будет линейной комбинацией всех этих состояний с некоторым комплексным коэффициентом.
А получить какое-то состояние можно измерением. Тогда мы получим результат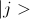 
с вероятностью 
.
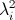Ancilla — вспомогательные кубиты, которые нужны при вычислении.
Так как вычисления на квантовом компьютере обратимы, то оператор, соответствующий булевой функции f будет действовать следующим образом:
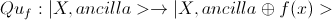. Очевидно, что обратный к этому оператору — он же сам.
Зеркальное отражение относительно гиперплоскости — оператор, действующий следующим образом:
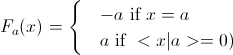
На произвольный вектор распространяется по линейности.
Алгоритм
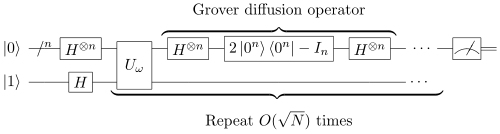
Пусть нам известно, что у f(x) = 1 есть L решений( L << N, в обратном случае мы сможет просто случайно выбирать x и с большой вероятностью наткнемся на решение).
Тогда пусть искомый вектор имеет вид:
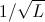
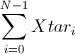, где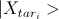 
— некоторое решение. При измерении такого состояния мы получим одно из решений.
Пусть начальное состояние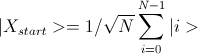 
— суперпозиция всех возможных состояний(базисных векторов), полученная действием элемента Уолша-Адамара на |0>.
Тогда для решения потребуется n+1 кубит, где первые n займет |X>, а последний — ancilla.
Установим анциллу в состояние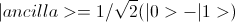 
, что получается действием элемента Адамара на |1>.
Тогдa, очевидно, что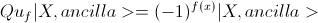 
, где |X> некоторый вектор состояния для n кубитов. (Что следует из тензорного произведения векторов и того, что 
).
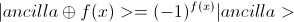То есть, Quf — задало зеркальное отражение относительно гиперплоскости, перпендикулярной вектору решений!
Зададим еще один оператор, который производит зеркальное отражение относительно вектора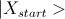 
:
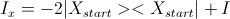, где I — единичная матрица. Не сложно проверить, что это верно определенный оператор.
Тогда пусть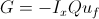 
— произведение(композиция) двух операторов. Тогда G задает поворот на некоторый угол 
.
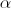Не сложно проверить, что этот угол равен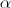 
= 
.
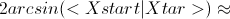
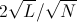Что следует из разложения арксинуса в ряд Тейлора при условии, что L << N.
Тогда G, действуя на |X>, поворачивает его на угол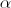 
в сторону 
!
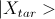А так как угол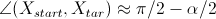
, то повторив операцию 
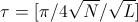раз, мы получим почти вектор 
!
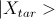Вероятность ошибки составит Perr = L/N, что при L << N дает гарантированный результат почти во всех случаях!
Заключение
Несмотря на то, что данный алгоритм имеет экспоненциальную сложность, он все-таки является примером, когда квантовый компьютер превосходит классический, ибо дает квадратичное ускорение в сравнении с классическими алгоритмами. Такую возможность нам дает тот факт, что мы можем делать поворот в сторону вектора решения, не зная сами решения.
Заранее приношу свои извинения за возможные ошибки/неточности в терминологии и описании алгоритма.
О всех подобных и орфографических ошибках прошу уведомлять в личку, чему буду рад, если оные найдутся!
Замечания приветствуются!
Автор: TakeOver
