И это не пузырьковая, а нечто гораздо более тупое.
Как-то после обеда, стоя в коридоре с чашечкой кофе, мне пришла в голову мысль. Что ведь для того, чтобы убедиться, что массив отсортирован, надо сделать всего n-1 сравнение. Например, для массива длины 4 таких сравнения будет 3:
if (a0 < a1 < a2 < a3) А получив утвердительный ответ на этот вопрос, мы можем сразу вернуть готовый массив:
if (a0 < a1 && a1 < a2 && a2 < a3) return [a0, a1, a2, a3];Клево! Теперь чтобы превратить это в сортировку 4 чисел осталось просто проверить все остальные комбинации максимально тупым образом:
def sort4(a0, a1, a2, a3) {
if (a0 < a1 && a1 < a2 && a2 < a3) return [a0, a1, a2, a3];
if (a0 < a1 && a1 < a2 && a3 < a2) return [a0, a1, a3, a2];
if (a0 < a2 && a2 < a1 && a1 < a3) return [a0, a2, a1, a3];
...
}
Оговорка
Строго говоря для того чтобы наша сортировка была стабильной, везде надо писать "<=" (меньше или равно), но меня задолбало это это набирать, так что я буду везде писать только "<". Упражнение по превращению этого удовольствия в продакшен-код я оставляю читателю.
Сколько таких комбинаций? Ну это легко. Их ровно 4! = 24. Мы только что придумали алгоритм с вычислительной сложностью O(n*n!). Это гораздо хуже пузырьковой сортировки (с его квадратичной асимптотикой) не только из-за ужасающе долгой работы, но и еще в добавок нам для массива каждой длины надо писать отдельную функцию. Жуть.
А факториал растет очень быстро, значит наши функции будут становиться все длиннее, отнимая не только вычисления, но и память - ее нам тоже потребуется O(n!). Не для хранения данных (мы же их даже никуда не сохраняем), а для самого алгоритма. Для всех "обычных" алгоритмов размер кода фиксирован, то есть O(1), и мы его просто игнорируем при оценке асимптотики по памяти. Для нашей "тупой" сортировки такое не прокатит.
Но давайте немного поразмышляем. Видим, что первые 3 случая повторяются в части нескольких первых сравнений. А что, если...
if a0 < a1:
if a1 < a2:
if a2 < a3:
return [a0, a1, a2, a3]
else:
if a1 < a3:
return [a0, a1, a3, a2]
else:
...
else:
...
....Хм. Давайте снова посчитаем вычислительную сложность. Кажется мы тут все наши возможные комбинации каждым сравнением делим примерно на 2. То есть вычислительная сложность сразу получает себе суперспособность логарифм: O(log(n!)).
То есть, если мы все правильно поняли, то мы только что придумали алгоритм, который сортированные списки обрабатывает за O(n) (самая первая ветка срабатывает за n-1 сравнение), а остальные случаи мы сортируем не хуже теоретически идеального случая. То есть как Quicksort, только без его "худшего" случая, когда он деградирует до "пузырька".

Расчехляем питон и пишем туда наш генератор тупых сортировок. Для начала возьмем и напишем функцию генерации перестановок:
def permutations(a: list[int]) -> list[list[int]]:
if len(a) == 1:
return [a]
return [
[a[i]] + recur
for i in range(len(a))
for recur in permutations(a[0:i] + a[i + 1:])
]Потом выкинем ее, вспомнив, что уже есть itertools.permutation() который делает ровно то же самое.
Теперь пишем 2 функции генерации строк:
def gen_comp(indent: int, l: int, r: int, s_then: str, s_else: str):
ind = "t" * indent
return ind + f"if a{l} < a{r}:n{s_then}n{ind}else:n{s_else}"
def gen_return(indent: int, indice: list[int]):
return "t" * indent + f"return [" + ", ".join([f"a{i}" for i in indice]) + "]"
Ну и саму функцию строящую дерево сравнений (осторожно, говнокод):
def gen_sort_n(cases: list[list[int]], known: list[tuple[int, int]], indent):
c = cases[0]
if len(cases) == 1:
return gen_return(indent, c)
lss, gtr = [], []
for l, r in list(zip(c, c[1:])):
if l == r or (l, r) in known or (r, l) in known:
continue
for c in cases:
(lss, gtr)[c.index(l) > c.index(r)].append(c) # Хитрый трюк с заполнением двух массивов за раз.
s_then = gen_sort_n(lss, known + [(l, r)], indent + 1)
s_else = gen_sort_n(gtr, known + [(r, l)], indent + 1)
return gen_comp(indent, l, r, s_then, s_else)
print(gen_sort_n(list(itertools.permutations(range(4))), [],0))
Она просто берет первую перестановку из переданных и сравнивает первую непроверенную пару элементов в ней. Потом все оставшиеся случаи раскидывает по подветкам true и false рекурсивно. Получаем на выходе код:
Много кода
if a0 < a1:
if a1 < a2:
if a2 < a3:
return [a0, a1, a2, a3]
else:
if a1 < a3:
return [a0, a1, a3, a2]
else:
if a0 < a3:
return [a0, a3, a1, a2]
else:
return [a3, a0, a1, a2]
else:
if a0 < a2:
if a1 < a3:
return [a0, a2, a1, a3]
else:
if a2 < a3:
return [a0, a2, a3, a1]
else:
if a0 < a3:
return [a0, a3, a2, a1]
else:
return [a3, a0, a2, a1]
else:
if a1 < a3:
return [a2, a0, a1, a3]
else:
if a0 < a3:
return [a2, a0, a3, a1]
else:
if a2 < a3:
return [a2, a3, a0, a1]
else:
return [a3, a2, a0, a1]
else:
if a0 < a2:
if a2 < a3:
return [a1, a0, a2, a3]
else:
if a0 < a3:
return [a1, a0, a3, a2]
else:
if a1 < a3:
return [a1, a3, a0, a2]
else:
return [a3, a1, a0, a2]
else:
if a1 < a2:
if a0 < a3:
return [a1, a2, a0, a3]
else:
if a2 < a3:
return [a1, a2, a3, a0]
else:
if a1 < a3:
return [a1, a3, a2, a0]
else:
return [a3, a1, a2, a0]
else:
if a0 < a3:
return [a2, a1, a0, a3]
else:
if a1 < a3:
return [a2, a1, a3, a0]
else:
if a2 < a3:
return [a2, a3, a1, a0]
else:
return [a3, a2, a1, a0]Выглядит вроде неплохо. А давайте посчитаем, какая средняя глубина вложенности if-ов при увеличении n. Для этого для каждого вызова gen_return запомним ident и просто посчитаем среднее. Код я тут опускаю, потому что он скучный, а терпение читателя не резиновое.
|
n |
n! |
Avg(indent) |
|
2 |
2 |
1.000 |
|
3 |
6 |
2.667 |
|
4 |
24 |
4.917 |
|
5 |
120 |
7.717 |
|
6 |
720 |
11.050 |
|
7 |
5040 |
14.907 |
|
8 |
40320 |
19.282 |
Давайте посмотрим, как эти числа ложатся на теорию.
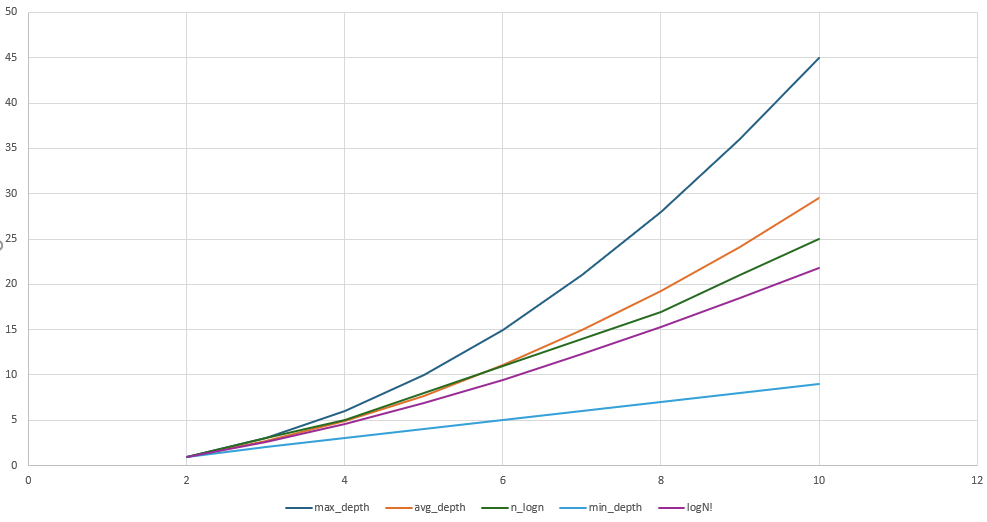
Что-то тут не так. Минимальная глубина, как и ожидалось, очень приятная = n-1, но вот оранжевая линия (средняя глубина) выше наших ожиданий. Мы же хотели O(n*logn), а тут явно что-то другое. Давайте внимательнее посмотрим на сгенеренный код. Некоторые перестановки (например return [a0, a3, a2, a1]) возвращаются только после 6 сравнений, тогда как теория предсказывает что их должно быть не больше 5 (столько сделает mergesort в худшем случае сортировки массива из 4 элеменов). Видно что это происходит из-за того что наши деревья сравнений не сбалансированы. То есть они не всегда делят количество вариантов пополам. Иногда пропорции оказываются гораздо хуже: 1 к 3 или даже 1 к 7. Так не пойдет. Давайте дерево балансировать.
Для этого переберем разные сравнения из доступных и выберем то, которое делит все случаи наилучшим образом (в пропорции 1:1).
Секретные материалы
Тут был график, который я где-то пролюбил, а заново искать и перезапускать старый код мне лень. Поэтому я прошу читателя мне поверить на слово, что там все было так, как описано ниже. А сам график был прекрасен как никогда так же скучен, как и первый, так что уважаемый читатель ничего не потерял. :-/
Статистика улучшилась, но опять не дотягивает до "идеальной". Еще немного поразмыслив, понимаем, что выбор "лучшего" доступного сравнения на данном шаге может привести к тому что, оставшиеся после деления варианты уже невозможно поделить поровну внутри рекурсивных вызовов.
Давайте тогда перепишем код чтобы он перебрал вообще все возможные последовательности проверок и вернул самую сбалансированную. Надо сказать, что такой перебор ужасно тормозит так как сложность такой генерации растет как квадрат факториала. Ради науки мы потерпим. Но только до n=5.
|
N |
depth |
|
2 |
[1, 1] |
|
3 |
[2, 3, 3, 2, 3, 3] |
|
4 |
[4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 5, 5, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 5, 5] |
|
5 |
[7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 6, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 6, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 6, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 6, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 6, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 6, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 6, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 6, 7, 7] |
Ну вот, совсем другое дело. Теперь взглянем на сгенеренный код для n=4.
if a0 < a1:
if a1 < a2:
if a1 < a3:
if a2 < a3:
return [a0, a1, a2, a3]
else:
return [a0, a1, a3, a2]
else:
if a0 < a3:
return [a0, a3, a1, a2]
else:
return [a3, a0, a1, a2]
else:
...Хм. Наша красивая первая "перестановка" теперь вместо 3 сравнений содержит 4. Причем "лишнее" сравнение (третье по счету) выглядит как-то совсем ненатурально. Однако статистика не врет - этот способ проверки самый лучший для среднего случая.
Но для среднего случая уже есть сортировка слиянием. Она гарантирует всегда близкое к идеальному количество сравнений. Лучше него только алгоритм слиянием-вставками и его вариации. Все они с фиксированным размером кода. Так нафига козе баян?
Дальше хуже
Для n=5 таких "ненужных" сравнений (для тривильного случая упорядоченнго массива) уже 7-4=3:
if a0 < a1:
if a2 < a3:
if a0 < a2:
if a2 < a4:
if a3 < a4:
if a1 < a3:
if a1 < a2:
return [a0, a1, a2, a3, a4]
else:
return [a0, a2, a1, a3, a4]
else:
if a1 < a4:
return [a0, a2, a3, a1, a4]
else:
return [a0, a2, a3, a4, a1]
else:
...Но можно подобрать параметры для оптимизации чтобы снизить это количество до 2.
И вот тут кажется мы можем нащупать какую-то пользу из нашего эксперимента. Мы получили действую модель оптимизации алгоритма под исходные данные. Если мы что-то знаем про частотность перестановок в исходных данных, мы можем подогнать под них алгоритм сортировки и получить гарантированно самую быструю сортировку. Быстрее теоретических чисел сортировки.
"Погодите-погодите" - скажет кто-то наивный - "ведь мы по прежнему имеем ужасную асимптотику по памяти и надо писать отдельную функцию для каждого n". На что мы имеем возразить:
-
Во первых очевидно, что его можно использовать только для небольших n. Вероятно не больше 7-8. После чего сгенеренный код начнет занимать уже непрактично много места. А если мы ограничиваем размер массива, то код становится конечным и наше использование памяти возвращается в приятное O(1).
-
Для больших n мы можем "сверху" на него надстроить обычную сортировку слиянием. Тем самым сильно ускорив сортировку для наших данных, а не сферических в вакууме.
-
Похожий трюк с подменой алгоритмов для сортировки массивов разной длины делают многие библиотеки. Скажем, заменяя на коротких массивах quicksort пузырьком потому что второй не использует рекурсию и начинает обгонять первого за счет меньшего оверхеда.
В качестве дальнейшей оптимизации нашего "супер-алгоритма" можно предложить:
-
Вместо возврата массивов генерить готовые операции in-place обмена элементов массива самым оптимальным образом (сдвигая подмассивы, где возможно, вместо перемещения поштучно). Либо делая идеальные циклические перестановки с единственным слотом:
temp = a0; a0 = a3; a3 = a2; a2 = tempдля варианта [a3, a1, a0, a2]) и т.п. -
Избавлять от ветвлений с помощью трюков branchless programming, переходя на векторные инструкции. Это должно дополнительно ускорять в разы и десятки раз.
На том и закончим наши размышления у кофе-машины и пойдем работать дальше, оставив задачу конечной реализации данного прорывного алгоритма студенту, которому нужна идея для курсовой...
Автор: barbalion






