В системах компьютерного зрения и обработки изображений часто возникает задача определения перемещений объектов в трехмерном пространстве с помощью оптического сенсора, то есть видеокамеры. Имея на входе последовательность кадров, необходимо воссоздать запечатленное на них трехмерное пространство и те изменения, которые происходят с ним с течением времени. Звучит сложно, но на практике зачастую достаточно найти смещения двухмерных проекций объектов в плоскости кадра.
Если мы хотим узнать на сколько тот или иной объект объект сместился по отношению к его же положению на предыдущем кадре за то время, которое прошло между фиксацией кадров, то скорее всего в первую очередь мы вспомним про оптический поток (optical flow). Для нахождения оптического потока можно смело воспользоваться готовой протестированной и оптимизированной реализацией одного из алгоритмов, например, из библиотеки OpenCV. При этом, однако, очень невредно разбираться в теории, поэтому я предлагаю всем заинтересованным заглянуть внутрь одного из популярных и хорошо изученных методов. В этой статье нет кода и практических советов, зато есть формулы и некоторое количество математических выводов.
Существует несколько подходов к определению смещений между двумя соседними кадрами. Например, можно для каждого небольшого фрагмента (скажем, 8 на 8 пикселей) одного кадра найти наиболее похожий фрагмент на следующем кадре. В этом случае разность координат исходного и найденного фрагментов даст нам смещение. Основная сложность тут состоит в том, как быстро отыскать нужный фрагмент, не перебирая весь кадр пиксель за пикселем. Различные реализации этого подхода так или иначе решают проблему вычислительной сложности. Некоторые настолько успешно, что применяются, например, в распространенных стандартах сжатия видео. Платой за скорость естественно является качество. Мы же рассмотрим другой подход, который позволяет получить смещения не для фрагментов, а для каждого отдельного пикселя, и применяется тогда, когда скорость не столь критична. Именно с ним в литературе часто связывают термин “оптический поток”.
Данный подход часто называют дифференциальным, поскольку в его основе лежит вычисление частных производных по горизонтальному и вертикальному направлениям изображения. Как мы увидим далее, одних только производных недостаточно чтобы определить смещения. Именно поэтому на базе одной простой идеи появилось великое множество методов, каждый из которых использует какую-нибудь свою математическую пляску с бубном, чтобы достичь цели. Сконцентрируемся на методе Лукаса-Канаде (Lucas-Kanade), предложенном в 81 году Брюсом Лукасом и Такео Канаде.
Метод Лукаса-Канаде
В основе всех дальнейших рассуждений лежит одно очень важное и не очень справедливое предположение: Предположим, что значения пикселей переходят из одного кадра в следующий без изменений. Таким образом, мы делаем допущение, что пиксели, относящиеся к одному и тому же объекту, могут сместиться в какую либо сторону, но их значение останется неизменным. Конечно же это предположение имеет мало общего с реальностью, потому что от кадра к кадру могут меняться глобальные условия освещения и освещенность самого движущегося объекта. Масса проблем связана с этим допущением, но, как ни странно, вопреки всему оно достаточно хорошо работает на практике.
На математическом языке это допущение можно записать так: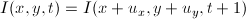 
. Где I — это функция яркости пикселей от положения на кадре и времени. Другими словами x и y — это координаты пикселя в плоскости кадра, 
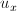и 
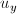— это смещение, а t — это номер кадра в последовательности. Условимся, что между двумя соседними кадрами проходит единичный отрезок времени.
Одномерный случай
Для начала рассмотрим одномерный случай. Представим себе два одномерных кадра 1 пиксель в высоту и 20 пикселей в ширину (рисунок справа). На втором кадре изображение немного смещено вправо. Именно это смещение мы и хотим найти. Для этого представим эти же кадры в виде функций (рисунок слева).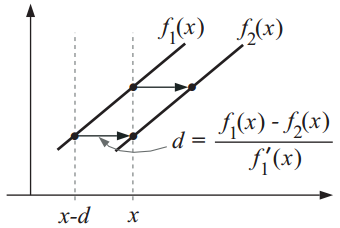 
На входе позиция пикселя, на выходе — его интенсивность. В таком представление искомое смещение (d) видно еще более наглядно. В соответствии с нашим предположением, 
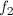это просто смещенная 
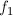, то есть можем сказать, что 
.
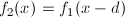Обратите внимание, что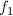 
и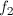 
при желании можно записать и в общем виде: 
; 
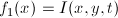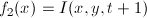где y и t зафиксированы и равны нулю.
Для каждой координаты нам известны значения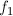 
и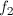 
в этой точке, кроме того мы можем вычислить их производные. Свяжем известные значения со смещением d. Для этого запишем разложение в ряд Тейлора для 
:
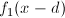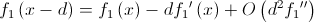
Сделаем второе важное предположение: Предположим, что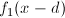 
достаточно хорошо аппроксимируется первой производной. Сделав это предположение, отбросим всё что после первой производной:
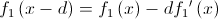
Насколько это корректно? В общем-то не очень, тут мы теряем в точности, если только наша функция/изображение не строго линейна, как в нашем искусственном примере. Зато это существенно упрощает метод, а для достижения требуемой точности можно сделать последовательное приближение, которе мы рассмотрим позже.
Мы почти у цели. Смещение d — это наша искомая величина, поэтому надо что-то сделать с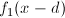 
. Как мы условились ранее, 
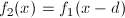, поэтому просто перепишем:
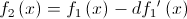
То есть:
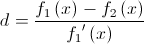
Двумерный случай
Теперь перейдем от одномерного случая к двумерному. Запишем разложение в ряд Тейлора для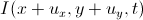 
и сразу отбросим все старшие производные. Вместо первой производной появляется градиент:
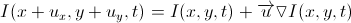
Где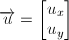 
— вектор смещения.
В соответствии со сделанным допущением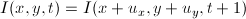 
. Обратите внимание, что это выражение эквивалентно 
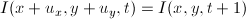. Это то, что нам нужно. Перепишем:
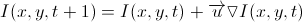
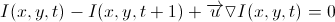
Поскольку между двумя кадрами проходит единичный интервал времени, то можно сказать, что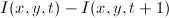 
есть не что иное, как производная по времени.
Перепишем:
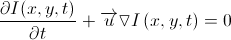
Перепишем ещё раз, раскрыв градиент:
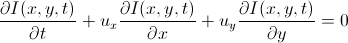
Мы получили уравнение, которое говорит нам о том, что сумма частных производных должны быть равна нулю. Проблема только в том, что уравнение у нас одно, а неизвестных в нем два: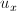 
и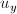 
. На этом моменте начинается полет фантазии и разнообразие подходов.
Сделаем третье предположение: Предположим, что соседние пиксели смещаются на одинаковое расстояние. Возьмем фрагмент изображения, скажем 5 на 5 пикселей, и условимся, что для каждого из 25 пикселе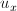й 
и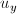 
равны. Тогда вместо одного уравнения мы получим сразу 25 уравнений! Очевидно, что в общем случае система не имеет решения, поэтому будем искать такие 
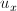и 
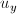, которые минимизируют ошибку:
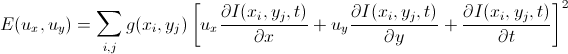
Здесь g — это функция, определяющая весовые коэффициенты для пикселей. Самые распространенный вариант — двухмерная гауссиана, которая дает наибольший вес центральному пикселю и все меньший по мере удаления от центра.
Чтобы найти минимум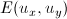 
воспользуемся методом наименьших квадратов, найдем её частные производные по 
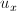и 
:
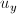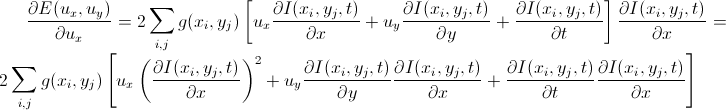
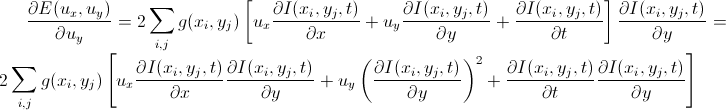
Перепишем в более компактной форме и приравняем к нулю:
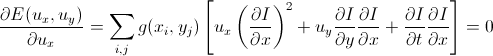
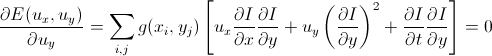
Перепишем эти два уравнения в матричной форме:
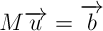
Где
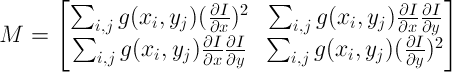
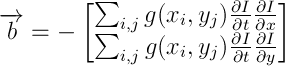
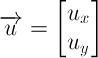
Если матрица М обратима (имеет ранг 2), можем вычислить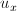 
и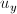 
, которые минимизируют ошибку E:
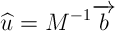
Вот собственно и все. Мы знаем приблизительное смещение пикселей между двумя соседними кадрами.
Поскольку в нахождении смещения каждого пикселя участвуют также соседние с ним пиксели, при реализации данного метода целесообразно предварительно посчитать производные кадра по горизонтали и вертикали.
Недостатки метода
Описанный выше метод основан на трех значительных допущениях, которые с одной стороны дают нам принципиальную возможность определить оптический поток, но с другой стороны вносят погрешность. Хорошая новость для перфекционистов состоит в том, что одно допущение нужно нам только для упрощения метода, и с его последствиями мы можем бороться.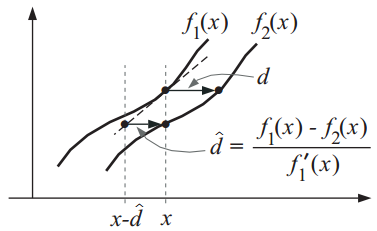 
Мы предполагали, что для аппроксимации смещения нам будет достаточно первой производной. В общем случае это конечно же не так (рисунок слева). Для достижение требуемой точности смещение для каждой пары кадров (назовём их 
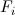и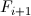 
) можно вычислять итеративно. В литературе это называется искажением (warping). На практике это означает, что, вычислив смещения на первой итерации, мы перемещаем каждый пиксель кадра 
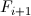в противоположную сторону так, чтобы это смещение компенсировать. На следующей итерации вместо исходного кадра 
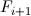мы будем использовать его искаженный вариант 
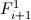. И так далее, пока на очередной итерации все полученные смещения не окажутся меньше заданного порогового значения. Итоговое смещение для каждого конкретного пикселя мы получаем как сумму его смещений на всех итерациях.
По своей природе данный метод является локальным, то есть при определении смещения конкретного пикселя принимается во внимание только область вокруг этого пикселя — локальная окрестность. Как следствие, невозможно определить смещения внутри достаточно больших (больше размера локальной окрестности) равномерно окрашенных участков кадра. К счастью на реальных кадрах такие участки встречаются не часто, но эта особенность все же вносит дополнительное отклонение от истинного смещения.
Ещё одна проблема связана с тем, что некоторые текстуры в изображении дают вырожденную матрицу М, для которой не может быть найдена обратная матрица. Соответственно, для таких текстур мы не сможем определить смещение. То есть движение вроде есть, но непонятно в какую сторону. В общем-то от этой проблемы страдает не только рассмотренный метод. Даже глаз человека воспринимает такое движение не однозначно (Barber pole).
Заключение
Мы разобрали теоретические основы одного из дифференциальных методов нахождения оптического потока. Существует множество других любопытных методов, некоторые из которых по состоянию на сегодняшний день дают более надежные результаты. Однако, метод Лукаса-Канаде при своей неплохой эффективности остается достаточно простым для понимания, а потому хорошо подходит для ознакомления с математическими основами.
Хотя проблема нахождения оптического потока изучается уже несколько десятилетий, методы всё ещё продолжают совершенствоваться. Работа продолжается в виду того, что при близком рассмотрении проблема оказывается очень непростой, а от качества определения смещений в обработке видео и изображений зависит устойчивость и эффективность многих других алгоритмов.
На этой пафосной ноте позвольте закруглиться и перейти к источникам и полезным ссылкам.
Источники и ссылки
1. Optical Flow Estimation. David J. Fleet, Yair Weiss. — Обстоятельная статья, которая содержит детальное описание не только метода Лукаса-Канаде, но и других дифференциальных методов.
2. Image and Video Compression for Multimedia Engineering: Fundamentals, Algorithms, and Standards. Yun Q. Shi, Huifang Sun — Учебник по сжатию видео и изображений, но содержит также неплохой обзор истории вопроса.
3. Image Processing On Line — Большое количество актуальных алгоритмов обработки изображений. Что самое приятное, алгоритмы снабжены онлайн демо.
Автор: Coderik
