Теоретические основы сплайн-интерполяции или почему IQ тесты не имеют решения

Доброго времени!

Куча времени прошла с того момента, как я написал свою первую статью, и уже почти год с того момента, как пришла в голову идея для второй. В силу многих обстоятельств (в первую очередь – лени и забывчивости), эта идея так и не была реализована ранее, но сейчас я собрался, написал весь этот материал и готов представить его вашему вниманию.

Начну с небольшой вводной. Будучи студентом 4-го, на тот момент, курса бакалавриата, я изучал курс «Компьютерная графика». Много там было разных интересных (и не очень) заданий, но одно прямо особо запало мне в душу: интерполяция кубическими сплайнами с заданными первыми производными на концах интервала. Пользователь должен был задавать значения первых производных, а программа — считать и выводить на экран интерполяционную кривую. Особенность и основная сложность задания заключена в том, что задаются именно первые производные, а не вторые, как в классической постановке сплайн-интерполяции.
Как я ее решал, и к чему оно в итоге пришло, я как раз и изложу в этой статье. И да, если по описанию задачи вы не поняли ни в чем ее смысл, ни в чем сложность, не переживайте, все это я также постараюсь раскрыть. Итак, поехали.

А, нет, погодите один момент. Вот вам два числовых ряда:
a) 2, 4, 6, 8, ?
b) 1, 3, ?, 7, 9

Какие числа должны стоять на месте вопросов и почему? Вы действительно уверены в своем ответе?

Интерполяция

Интерполяция, интерполирование (от лат. inter-polis – «разглаженный, подновлённый, обновлённый; преобразованный») – в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. (с) Википедия

Поясню на примерах. Существуют задачи, когда нам требуется узнать, условно, «закон распределения» (взял в кавычки, так как это, вообще говоря, термин из другой области математики) некого параметра по нескольким известным его значениям. Чаще всего речь идет об изменении некого параметра во времени: координаты движущегося тела, температуры объекта, колебания курса валюты, etc. При этом в силу каких-либо обстоятельств у нас не было возможности наблюдать за этим параметром непрерывно, мы могли узнавать его значения лишь в какие-то отдельные моменты времени. Исходными данными в таком случае у нас является множество точек вида value(time), а целью задачи – восстановить кривую, проходящую через эти точки и непрерывно описывающую изменение этого параметра.

Следует понимать, что невозможность постоянного наблюдения за соответствующим параметром – это обычно какого-либо рода технологическое ограничение. С развитием техники таких ситуаций становится все меньше и меньше. Из современных задач такого плана – траектория движения, например, марсохода. Поддерживать непрерывный сеанс связи (пока что) все еще не представляется возможным, а контролировать его перемещение и рисовать красивые траектории хочется. Получается, что конкретные координаты можно узнать только в те моменты, когда связь все-таки налажена, а траекторию целиком приходится восстанавливать по полученным таким образом время от времени точкам.
Другой вариант применения интерполяции. Некоторые современные телевизоры показывают изображение с частотой обновления картинки до >=1000Гц (хотя это все еще запредельные значения). Большинство телевизоров так не умеет, но даже так многие отображают картинку на частоте 100Гц — такая величина уже вполне себе классика. А если верить википедии, то в кинематографе «частота 24 кадра в секунду является общемировым стандартом». Для того, чтобы превратить 24 кадра в секунду исходного видеопотока в 100 кадров в секунду результата, телевизор использует интерполяцию. А именно какие-нибудь алгоритмы в стиле «взять два соседних кадра 1 и 2, посчитать разницу между ними и сформировать из нее 3 дополнительных кадра, которые надо впихнуть между теми двумя изначальными» -> получаются кадры 1, 1_1, 1_2, 1_3, 2

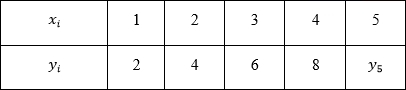
Для дальнейших рассуждений возьмем более простой пример. Представим себе, например, лабораторную работу по географии в каком-нибудь 6-ом классе (кстати, у меня когда-то и правда была такая). Необходимо каждые 3 часа измерять температуру воздуха и записывать данные, а потом сдать учителю график изменения температуры от времени суток. Допустим, по результатам измерений у нас получилась вот такая табличка (данные придуманы случайным образом и никак не претендуют на какую-либо правдоподобность):

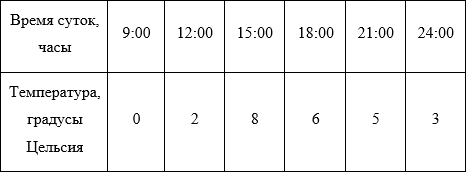
Отобразим полученные данные на графике:

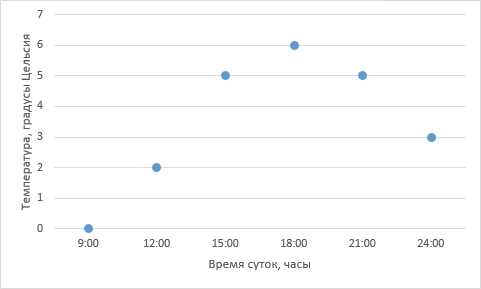
Собственно, данные записаны и отражены на графике. Мы вплотную подошли к задаче интерполяции – как по имеющимся точкам восстановить плавную кривую?

Количество условий и степень интерполирующего полинома

Можем ли мы вообще гарантировать, что такая функция, которая соединяет все заданные точки, вообще существует?

Да, такая функция гарантированно существует, и более того, таких функций будет бесконечно много. Для любого набора точек можно будет придумать сколько угодно много функций, которые через них будут проходить. И вот несколько примеров того, как две точки можно соединить разными способами:

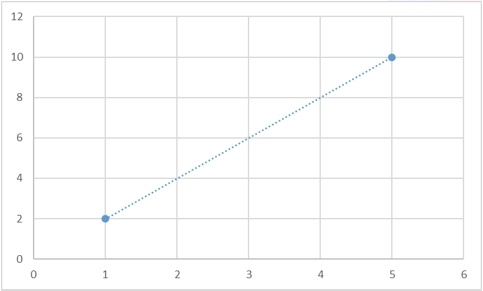
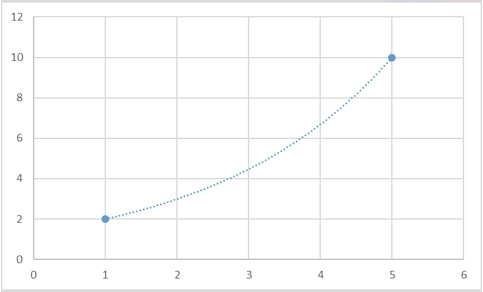
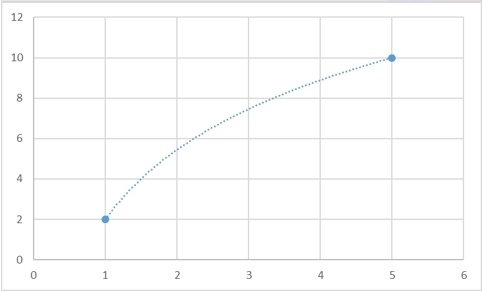
Однако есть и способ задать интерполяционную кривую однозначно. В самом классическом случае, в качестве интерполяционной кривой берут полином:

Для того, чтобы провести через имеющиеся точки такой полином единственным образом, необходимо и достаточно, чтобы степень полинома была на 1 меньше, чем количество условий (я специально выделил это слово, потому что в конце этого раздела я вернусь к этой формулировке). Пока что, простоты ради, условием будут являться координаты точки. Говоря человеческим языком, через 2 точки однозначным образом можно провести прямую (полином 1-ой степени), через 3 точки – параболу (полином 2-ой степени) и т.д.

Возвращаясь к нашей задаче с температурой – в ней мы определили 6 точек, значит, для того, чтобы провести полином единственным образом, он должен быть 5-ой степени

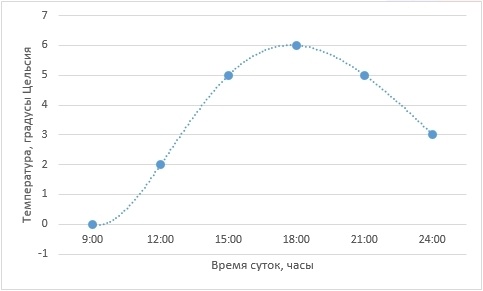
Интерполирующий полином тогда будет выглядеть так:

$inline$-frac{x^5}{14580}+frac{13x^4}{1944}-frac{41x^3}{162}+frac{983x^2}{216}-frac{2273x}{60}+117$inline$

А сейчас следует сделать важное замечание и пояснить, что я имел ввиду под «условием». Полином можно задать не только координатами точек, через которые он проходит, условиями могут быть любые параметры этого полинома. В простейшем случае это действительно координаты точек. Но в качестве условия можно взять, например, первую производную этого полинома в какой-либо из точек. Вторую производную. Третью производную. В общем, любую возможную производную в любой из точек, в которой этот полином существует. Поясню на примере:
Прямую можно задать однозначно, как я уже говорил, двумя точками:

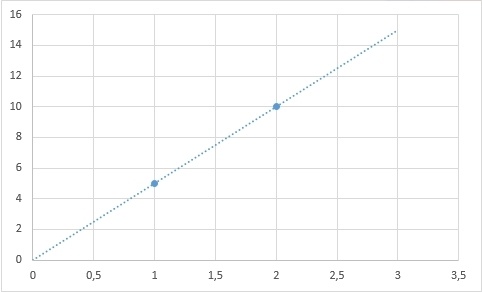
Ту же прямую, с другой стороны, можно определить координатой одной точки и углом наклона альфа к горизонтали:

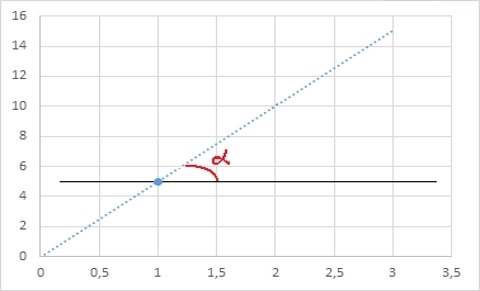
С полиномами более высоких степеней можно использовать и более сложные условия (вторая производная, третья производная, etc.), и каждый такой параметр будет идти в общий счет количества условий, которые однозначным образом определят этот полином. Чтобы не быть голословным, вот еще пример:

Пусть нам заданы такие три условия:

Условий три, значит, мы хотим получить полином второй степени:

Подставляем

Считаем первую производную и считаем

Считаем вторую производную и считаем

Отсюда получаем, что наш полином выглядит так:

Интерполяция кубическими сплайнами

Вот, по тиху, мы и подбираемся к моей задаче. Полиномиальная интерполяция – не единственно возможный способ интерполяции. Среди всех прочих методов существует метод интерполяции кубическими сплайнами.

Принципиальное отличие идеи сплайн-интерполяции от интерполяции полиномом состоит в том, что полином один, а сплайн состоит из нескольких полиномов, а именно их количество равно количеству инервалов, внутри которых мы производим интерполяцию. В примере с нашей температурой воздуха, в которой у нас определено 6 точек, у нас будет 5 интервалов – соответственно, у нас будут 5 полиномов, каждый на своем интервале.

Каждый из этих полиномов – это полином третьей степени (строго говоря, степени не выше третьей, так как на каком-то из интервалов интерполирующая кривая может становиться квадратичной параболой или даже линейной функцией, но в общем случае это все-таки полином именно третьей степени). Записывая вышесказанное формульно, получим что все наши точки будут соединены некоей кривой , где каждый – это полином третьей степени, а именно:

Возвращаясь к рассказанному в предыдущем пункте, для того, чтобы однозначно задать один полином 3-ей степени, необходимо 4 условия. В этой задаче у нас 5 полиномов, то есть, чтобы задать их все, нам нужно суммарно 5∙4=20 условий. И вот как они получаются:

1) Первый полином определен на первой и второй точках – это два условия. Второй полином определен на второй и третьей точках – еще два условия. Третий полином, четвертый, пятый – каждый из них определен на 2-х точках – суммарно это дает 10 условий.

2) Для каждой промежуточной точки из множества (а это 4 точки с временами 12:00, 15:00, 18:00, 21:00) должно выполняться условие, что первые и вторые производные для левого и правого полиномов должны совпадать. Формульно:

По два таких условия на каждую из промежуточных точек дает еще 8 условий. Следует добавить, что мы задаем только сам факт равенства, а какое конкретно значение они при этом принимают – это совершенно иная задача и считается она довольно сложно.

3) Остаются два условия, которые пока еще не определены. Это так называемые «граничные условия», от задания которых и зависит, какой именно сплайн получится. Обычно задают вторые производные на концах интервала равными 0:

Если сделать так, то мы получим так называемый «естественный сплайн». Для вычисления таких сплайнов написано уже огромное количество библиотек, бери и используй любую.

Отличие моего задания от классической постановки задачи, мои размышления над заданием и само решение

И вот мы подошли к условию моей задачи. Преподаватель придумал такое задание, что задаваться должны первые производные и на левом и правом концах интервала, а программа должна считать интерполирующую кривую. А для такого требования готовых алгоритмов я не нашел…
Я, разумеется, не стану описывать весь твой «творческий» путь от момента, когда я услышал задание, до того, как я его сдал. Расскажу лишь саму идею и покажу ее реализацию.

Сложность задания состоит в том, что, задавая первые производные на концах интервала, да, мы задаем этот сплайн. Теоретически. А вот посчитать его на практике – задача довольно сложная и совершенно неочевидная (желающие могут посмотреть код нахождения естественного сплайна на Вики – ru.wikipedia.org/wiki/Кубический_сплайн – и попробовать его понять хотя бы). Разумеется, я совершенно не хотел провести кучу времени, закопавшись в матан и пытаясь вывести нужные мне формулы. Я хотел более простое и элегантное решение. И я его нашел.
Рассмотрим наш сплайн и возьмем первый из его интервалов. На этом интервале уже заданы 3 условия:

— задается пользователем

Для того, чтобы однозначно задать кубический полином на этом интервале, нам не хватает еще лишь одного условия. Но мы можем его просто придумать! Возьмем вторую производную и положим ее равной, например, 0:

— ничем не обоснованное предположение

Таким образом, зная эти 4 условия, мы полностью определяем этот полином. Зная все параметры этого полинома, мы можем вычислить значения первой и второй производных на второй точке, и поскольку они совпадают со значениями первой и второй производной для полинома на втором интервале, это приводит к тому, что мы также определяем и второй полином:

— вычисляется из

— вычисляется из

Аналогично мы считаем третий полином, четвертый, пятый и так далее, сколько бы их ни было. То есть, по факту, воссоздаем весь сплайн. Но поскольку мы взяли совершенно случайным образом, это приведет к тому, что производная , заданная пользователем на правом конце сплайна, не будет совпадать с производной , которая получилась у нас в ходе таких вычислений. Но получается, что значение производной на правом конце сплайна – это функция, зависящая от значения второй производной на левом конце:

А поскольку такой сплайн, который бы удовлетворял заданным условиям, гарантированно существует, и существует в единственном экземпляре, это значит, что мы можем рассмотреть разность:

и попытаться найти такое значение , при котором обращалась бы в 0 – и это будет тем самым правильным значением , которое строит искомый пользователем сплайн:

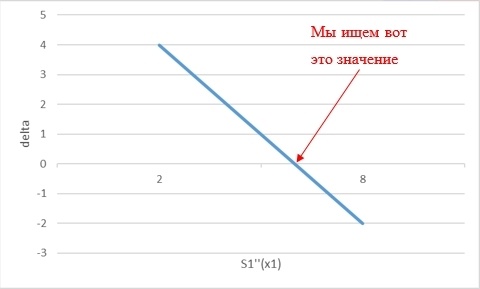
Самое замечательное в моей идее то, что эта зависимость оказалась линейной (вне зависимости от количества точек, через которые мы проводим сплайн. Этот факт доказан теоретическими подсчетами), а значит можно случайным образом взять любые два начальные значения и , посчитать и , и сразу же посчитать то самое верное значение, которое построит нам искомый сплайн:

Итого, мы гарантированно находим искомый сплайн за 3 прогонки таких вычислений.

Немного кода и скриншотов программы

class CPoint
{
    public int X { get; }
    public int Y { get; }

    public double Df { get; set; }
    public double Ddf { get; set; }

    public CPoint(int x, int y)
    {
        X = x;
        Y = y;
    }
}

class CSplineSubinterval
{
    public double A { get; }
    public double B { get; }
    public double C { get; }
    public double D { get; }

    private readonly CPoint _p1;
    private readonly CPoint _p2;

    public CSplineSubinterval(CPoint p1, CPoint p2, double df, double ddf)
    {
        _p1 = p1;
        _p2 = p2;

        B = ddf;
        C = df;
        D = p1.Y;
        A = (_p2.Y - B * Math.Pow(_p2.X - _p1.X, 2) - C * (_p2.X - _p1.X) - D) / Math.Pow(_p2.X - _p1.X, 3);
    }

    public double F(int x)
    {
        return A * Math.Pow(x - _p1.X, 3) + B * Math.Pow(x - _p1.X, 2) + C * (x - _p1.X) + D;
    }

    public double Df(int x)
    {
        return 3 * A * Math.Pow(x - _p1.X, 2) + 2 * B * (x - _p1.X) + C;
    }

    public double Ddf(int x)
    {
        return 6 * A * (x - _p1.X) + 2 * B;
    }
}

class CSpline
{
    private readonly CPoint[] _points;
    private readonly CSplineSubinterval[] _splines;

    public double Df1
    {
        get { return _points[0].Df; }
        set { _points[0].Df = value; }
    }
    public double Ddf1
    {
        get { return _points[0].Ddf; }
        set { _points[0].Ddf = value; }
    }
    public double Dfn
    {
        get { return _points[_points.Length - 1].Df; }
        set { _points[_points.Length - 1].Df = value; }
    }
    public double Ddfn
    {
        get { return _points[_points.Length - 1].Ddf; }
        set { _points[_points.Length - 1].Ddf = value; }
    }

    public CSpline(CPoint[] points)
    {
        _points = points;
        _splines = new CSplineSubinterval[points.Length - 1];
    }

    public void GenerateSplines()
    {
        const double x1 = 0;
        var y1 = BuildSplines(x1);
        const double x2 = 10;
        var y2 = BuildSplines(x2);

        _points[0].Ddf = -y1 * (x2 - x1) / (y2 - y1);

        BuildSplines(_points[0].Ddf);

        _points[_points.Length - 1].Ddf = _splines[_splines.Length - 1].Ddf(_points[_points.Length - 1].X);
    }

    private double BuildSplines(double ddf1)
    {
        double df = _points[0].Df, ddf = ddf1;
        for (var i = 0; i < _splines.Length; i++)
        {
            _splines[i] = new CSplineSubinterval(_points[i], _points[i + 1], df, ddf);

            df = _splines[i].Df(_points[i + 1].X);
            ddf = _splines[i].Ddf(_points[i + 1].X);

            if (i < _splines.Length - 1)
            {
                _points[i + 1].Df = df;
                _points[i + 1].Ddf = ddf;
            }
        }
        return df - Dfn;
    }
}

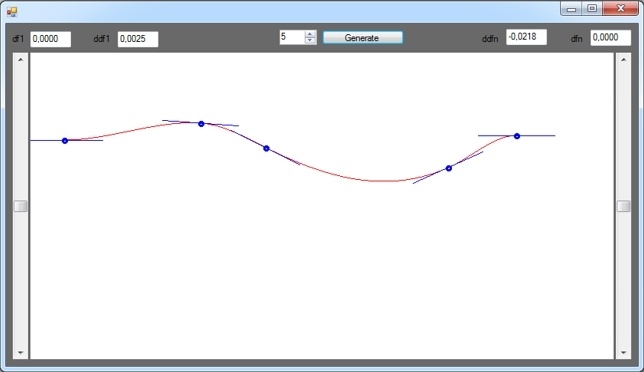
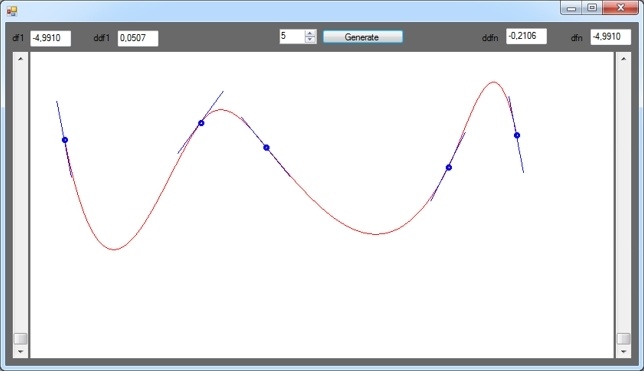
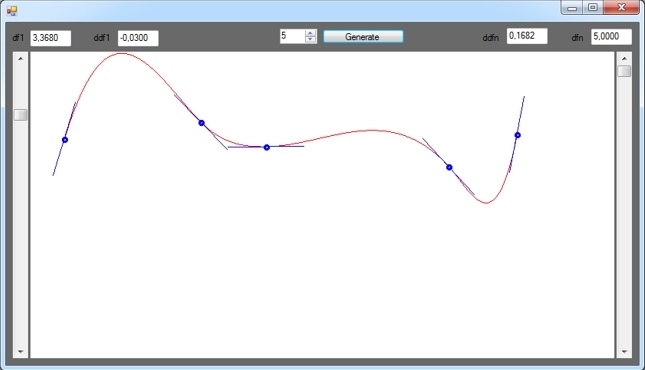
Синие отрезки — это первые производные сплайна в соответствующих его точках. Добавил такой вот графический элемент для большей наглядности.

Достоинства и недостатки алгоритма

Признаюсь честно, я не проводил сколь-либо серьезного анализа. По-хорошему стоило бы написать тесты, проверить, как оно работает в разных условиях (мало/много точек интерполяции, равное/произвольное между точками, линейные/квадратные/кубические/тригонометрические/etc. функции и так далее), но я этого не сделал, простите :)

Навскидку можно сказать, что сложность алгоритма — O(N), так как, как я уже говорил, вне зависимости от количества точек, достаточно двух прогонов вычислений, чтобы получить правильное значение второй производной на левом конце интервала, и еще одного, чтобы построить сплайн.

Впрочем, если кому-то захочется покопаться в коде и провести какой-нибудь более подробный анализ этого алгоритма, я буду только рад. Напишите мне разве что о результатах, мне было бы интересно.

Так а в чем провинились тесты IQ?

В самом начале статьи я написал два числовых ряда и попросил их продолжить. Это довольно частый вопрос во всяких IQ тестах. В принципе, вопрос как вопрос, но если копнуть чуть глубже, окажется, что он довольно бредовый, потому что при некотором желании можно доказать, что «правильного» ответа на него не имеется.

Рассмотрим для начала ряд «2, 4, 6, 8, ?»
Представим себе этот числовой ряд как множество пар значений :

, где в качестве мы берем само число, а в качестве – порядковый номер этого числа. Какое значение должно быть на месте ?

Мысль, к которой я стараюсь плавно подвести – это то, что мы можем подставить абсолютно любое значение. Ведь что по факту проверяют такие задачи? Способность человека найти некое правило, которое связывает все имеющиеся числа, и по этому правилу вывести следующее число в последовательности. Говоря научным языком, здесь стоит задача экстраполяции (задача интерполяции состоит в том, чтобы найти кривую, проходящую через все точки внутри некоторого интервала, а задача экстраполяции – продолжить эту кривую за пределы интервала, «предсказав» таким образом поведение кривой в дальнейшем). Так вот, экстраполяция не имеет однозначного решения. Вообще. Никогда. Если бы было иначе, люди давным-давно бы предсказали прогноз погоды на всю историю человечества вперед, а скачки курса рубля никогда не были бы неожиданностью.

Разумеется, предполагается, что верный ответ в этой задаче все-таки есть и он равен 10, и тогда «закон», связывающий все эти числа, – это

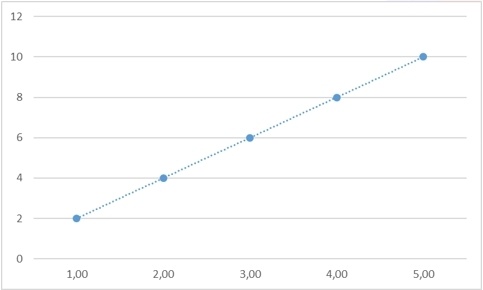
Однако возьмем любое другое значение – и мы также сможем найти закон, который бы обосновывал именно его:

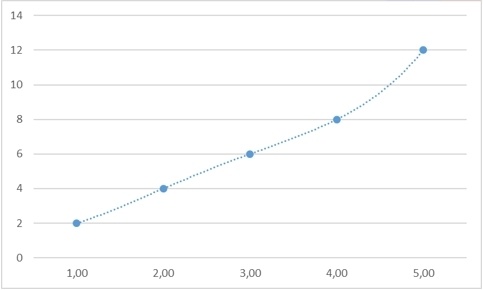
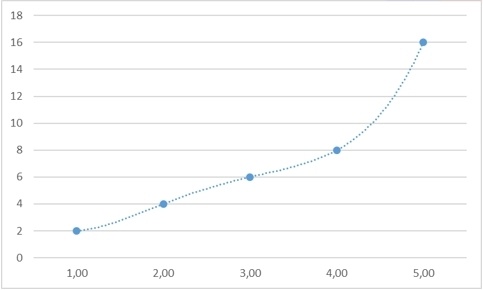
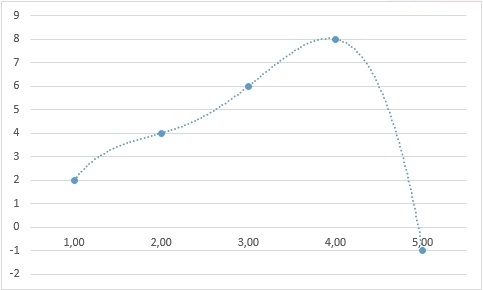
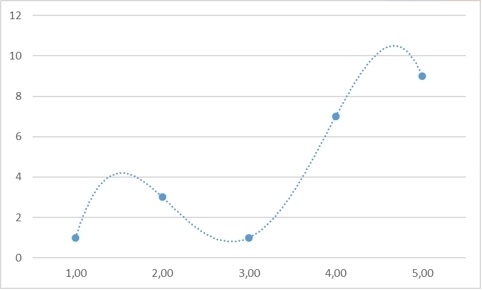
Хорошо, с экстраполяцией разобрались, она не имеет однозначного решения даже теоретически. Но, быть может, мы сможем найти пропущенное число во втором ряду?

Я считаю, верный ответ . Кто сможет оспорить? :)

Git-репозиторий

В прошлый раз меня ругали за то, что я выложил проект в виде архива в облаке, а не в виде кодов в репозиторий, поэтому в этот раз я исправляю эту свою ошибку: github.com/WieRuindl/Splines

Автор: WieRuindl

Источник