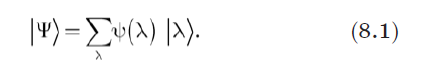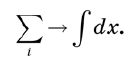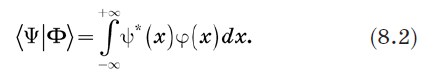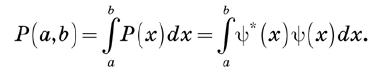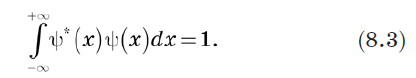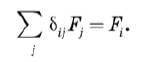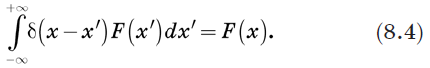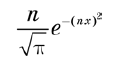Классическая механика интуитивна: она ежедневно и многократно используется людьми для выживания. Но до двадцатого века никто и никогда не использовал квантовую механику. Она описывает вещи столь малые, что они полностью выпадают из области восприятия человеческих органов чувств. Единственный способ понять эту теорию, насладиться ее красотой — перекрыть нашу интуицию абстрактной математикой.
Леонард Сасскинд — известный американский ученый — приглашает вас отправиться в увлекательное путешествие в страну квантовой механики. В пути вам пригодятся базовые знания из школьного курса физики, а также основы математического анализа и линейной алгебры. Также необходимо знать кое-что о вопросах, которые рассматривались в первой книге «теоретического минимума» Сасскинда — «Все, что нужно знать о современной физике». Но нестрашно, если эти знания несколько подзабылись. Многое автор напомнит и пояснит по ходу дела.
Квантовая механика — необычная теория: согласно ее постулатам, например, мы можем знать все о системе и ничего о ее отдельных частях. По поводу этого и других противоречий в свое время много спорили Эйнштейн и Нильс Бор. Если вы не боитесь сложностей, обладаете пытливым умом, технически грамотны, искренне и глубоко интересуетесь физикой, то этот курс лекций Леонарда Сасскинда придется вам по душе. Книга концентрируется на логических принципах квантовой теории и ставит целью не сгладить парадоксальность квантовой логики, а вытащить ее на дневной свет и попытаться разобраться с непростыми вопросами, которые она поднимает.
Обзор волновой функции
В этой лекции мы будем использовать язык волновых функций, поэтому давайте перед погружением сделаем небольшой обзор материала. Мы обсуждали в лекции 5 волновые функции абстрактных объектов, не объясняя, какое они имеют отношение к волнам или функциям. Прежде чем восполнить этот пробел, я напомню то, что мы обсуждали ранее.
Начнем с того, что выберем наблюдаемую L с собственными значениями l и собственными векторами |l〉. Пусть |Y〉 будет вектором состояния. Поскольку собственные векторы эрмитова оператора образуют полный ортонормированный базис, вектор |Y〉 можно разложить по этому базису:
Как вы помните из разделов 5.1.2 и 5.1.3, величины Y(l) называются волновой функцией системы. Но заметьте: конкретная форма Y(l) зависит от конкретной наблюдаемой L, которую мы первоначально выбрали. Если выбрать другую наблюдаемую, волновая функция (наряду с базисными векторами и собственными значениями) окажется иной, несмотря на то что мы по-прежнему говорим о том же самом состоянии. Таким образом, мы должны сделать оговорку о том, что Y(l) является волновой функцией, связанной с |Yñ. Если быть точными, мы должны сказать, что Y(l) является волновой функций в L-базисе. Если использовать свойства ортонормированности этого базиса векторов 〈li|lj〉 = dij, то волновая функция в этом L-базисе может быть также задана с помощью внутренних произведений (или проекций) вектора состояния |Y〉 на собственные векторы |l〉: Y(l) = 〈l|Y〉
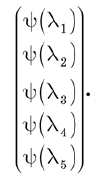
О волновой функции можно думать двумя способами. Прежде всего, это набор компонент вектора состояния в конкретном базисе. Эти компоненты можно выписать в форме вектора столбца:
Другой способ думать о волновой функции — это рассматривать ее как функцию l. Если вы задали любое допустимое значение l, то функция Y(l) дает комплексное число. Можно, таким образом, сказать, что Y(l) —это комплекснозначная функция дискретной переменной l. При таком рассмотрении линейные операторы становятся операциями, которые применяются к функциям и дают новые функции.
И еще одно, последнее напоминание: вероятность того, что эксперимент даст результат l, равна P(l) = Y*(l)Y(l).
Функции и векторы
До сих пор системы, которые мы изучали, имели конечномерные векторы состояния. Например, простой спин описывается двумерным пространством состояний. По этой причине наблюдаемые имели только конечное число возможных наблюдаемых значений. Но существуют более сложные наблюдаемые, которые могут иметь бесконечное число значений. Примером служит частица. Координаты частицы являются наблюдаемыми, но в отличие от спина координаты имеют бесконечное число возможных значений. Например, частица, движущаяся вдоль оси x, может находиться у любой вещественной отметки x. Другими словами, x является непрерывной бесконечной переменной. Когда наблюдаемые системы непрерывны, волновая функция становится полноценной функцией непрерывной переменной. Для применения квантовой механики к системам такого рода мы должны расширить представление о векторах так, чтобы включить в него функции.
Функции являются функциями, а векторы — векторами; они кажутся совершенно разными сущностями, так в каком же смысле функции являются векторами? Если вы думаете о векторах как о стрелках в трехмерном пространстве, то они, конечно, совсем не то же самое, что функции. Но если вы взглянете на векторы шире, как на математические объекты, удовлетворяющие некоторым постулатам, функции в действительности образуют векторное пространство. Такое векторное пространство часто называют гильбертовым пространством в честь математика Давида Гильберта.
Рассмотрим набор комплексных функций Y(x) одной вещественной переменной x. Под комплексной функцией я имею в виду, что каждому x она сопоставляет комплексное число Y(x). С другой стороны, независимая переменная x является обычной вещественной переменной. Она может принимать любые вещественные значения от –∞ до +∞.
Теперь сформулируем точно, что мы имеем в виду, говоря, что «функции являются векторами». Это не поверхностная аналогия или метафора. При некоторых ограничениях (к которым мы еще вернемся) такие функции, как Y(x), удовлетворяют математическим аксиомам, которые определяют векторное пространство. Мы вскользь упоминали эту идею в разделе 1.9.2, а теперь используем ее в полную силу. Оглядываясь назад, на аксиомы комплексного векторного пространства (в разделе 1.9.1), мы видим, что комплексные функции удовлетворяют им всем.
1. Сумма любых двух функций является функцией.
2. Сложение функций коммутативно.
3. Сложение функций ассоциативно.
4. Существует единственная нулевая функция такая, что при ее сложении с любой функцией получается та же самая функция.
5. Для любой данной функции Y(x) существует единственная функция –Y(x), такая что Y(x) + (–Y(x)) = 0.
6. Умножение функции на любое комплексное число дает функцию и является линейным.
7. Соблюдается дистрибутивное свойство, означающее что
z[Y(x) + j(x)] = zY(x) + zj(x),
[z + w]Y(x) = zY(x) + wY(x),
где z и w — комплексные числа.
Все это подразумевает, что мы можем идентифицировать функцию Y(x) с кет-вектором |Y〉 в абстрактном векторном пространстве. Неудивительно, что мы также можем определить бра-векторы. Бра-вектор 〈Y|, соответствующий кету |Y〉, отождествляется с комплексно сопряженной функцией Y*(x).
Для эффективного использования этой идеи нам необходимо обобщить некоторые предметы из нашего набора математических инструментов. В предыдущих лекциях метки, которые идентифицировали волновые функции, были членами некоего конечного дискретного множества, например собственными значениями определенной наблюдаемой. Но теперь независимая переменная непрерывна. Среди прочего это означает, что мы не можем суммировать по ней, пользуясь обычными суммами. Я думаю, вы знаете, что надо делать. Вот ориентированные на функции заменители для трех наших векторных понятий, с двумя из которых вы уже знакомы.
• Суммы заменяются интегралами.
• Вероятности заменяются плотностями вероятности.
• Дельта-символ Кронекера заменяется дельта-функцией Дирака.
Присмотримся к этим инструментам внимательнее.
Суммы заменяются интегралами. Если мы по-настоящему хотели бы сохранить строгость, то начали бы с замены оси x дискретным набором точек, разделенных очень малыми интервалами ε, а затем перешли бы к пределу ε → 0. Понадобилось бы несколько страниц на то, чтобы обосновать каждый шаг. Но мы можем избежать этих хлопот с помощью нескольких интуитивных определений, таких как замена сумм интегралами. Схематически этот подход можно записать так:
Например, если надо вычислить площадь под кривой, ось x делится на крошечные отрезки, затем складываются площади большого числа прямоугольников, в точности как это делается в элементарном математическом анализе. Когда мы даем отрезкам сжиматься до нулевого размера, сумма становится интегралом.
Рассмотрим бра 〈Y| и кет |Y〉 и определим их внутреннее произведение. Очевидный способ сделать это состоит в замене суммирования в уравнении (1.2) на интегрирование. Мы определим внутреннее произведение так:
Вероятности заменяются плотностями вероятности. Далее, мы отождествим P(x) = Y*(x)Y(x) с плотностью вероятности для переменной x. Почему именно с плотностью вероятности, а не просто с вероятностью? Если x является непрерывной переменной, то вероятность, что она примет любое точно заданное значение, обычно равна нулю. Поэтому правильнее ставить вопрос так: какова вероятность того, что x лежит между двумя значениями x = a и x = b? Плотность вероятности определяется так, что эта вероятность дается интегралом
Поскольку полная вероятность должна быть 1, мы можем определить нормировку вектора как
Дельта-символ Кронекера заменяется дельта-функцией Дирака. До сих пор все было очень знакомо. Дельта функция Дирака — это что-то новенькое. Дельта-функция является аналогом дельта-символа Кронекера dij, который по определению равен 0, если i ≠ j, и 1, если i = j. Но его можно определить и по-другому. Рассмотрим любой вектор Fi в конечномерном пространстве. Легко заметить, что дельта-символ Кронекера удовлетворяет условию
Это связано с тем, что в данной сумме ненулевыми являются только члены с j = i. В ходе суммирования символ Кронекера отфильтровывает все компоненты F кроме Fi. Очевидным обобщением этого будет определить новую функцию, которая обладает таким же фильтрующим свойством, когда используется под интегралом. Другими словами, нам нужна новая сущность d(x – x'), обладающая тем свойством, что для любой функции F(x)
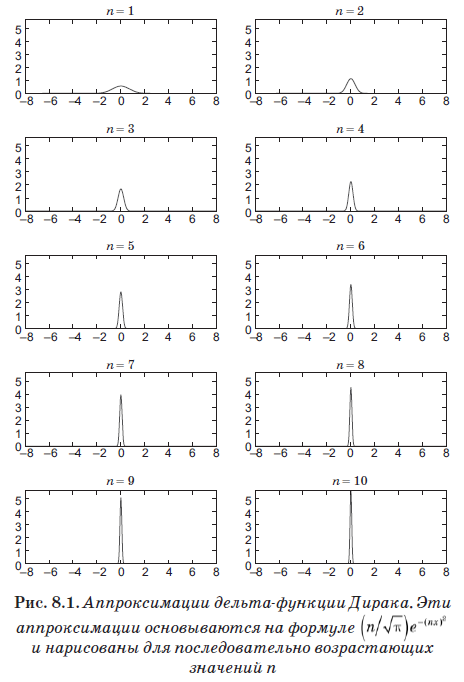
Уравнение (8.4) определяет новую сущность, называемую дельта-функцией Дирака, которая оказалась важнейшим инструментом в квантовой механике. Но несмотря на ее название, это в действительности не функция в обычном смысле. Она равна нулю везде, где x ≠ x', но когда x = x' она обращается в бесконечность. Фактически она бесконечна ровно настолько, чтобы площадь под d(x) была равна 1. Грубо говоря, эта функция отлична от нуля на бесконечно малом интервале ε, но на этом интервале имеет значение 1/ε. Таким образом, площадь под ней равна 1, и, что важнее, она удовлетворяет уравнению (8.4). Функция
достаточно хорошо аппроксимирует дельта-функцию при очень больших значениях n. На рис. 8.1 показана эта оптимизация при увеличивающихся значениях n. Несмотря на то что мы остановились на n = 10, то есть очень небольшом значении, обратите внимание, что график уже стал очень узким и резким пиком.
» Более подробно с книгой можно ознакомиться на сайте издательства
» Оглавление
» Отрывок
Для читателей данного блога скидка 20% по купону — Сасскинд
Автор: ph_piter
