Написать этот пост меня привлекла эта статья. Многие ее помнят по вот этой картинке.
Статья затрагивает правильную тему, однако с точки зрения математики и здравого смысла она в корне не верна.
Для не читавших ее напомню: в ней идет речь о сортировке контента на основе оценок пользователя. Основная проблема в том, что если у какой-то статьи (или товара) всего одна оценка в 5 балов, то его рейтинг будет выше чем у статьи с сотней голосов в пять балов и одним в 4ре бала.
Математика
Автор предлагает использовать формулу, которая была написана на стекле в фильма «Социальная сеть»:
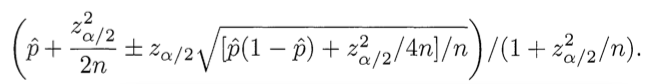
доверительный интервал Вильсона.
Это звучит, конечно, серьезно, однако нет никакого основания применять эту формулу к задаче, кроме одного эпизода из фильма, снятого по бульварному роману. Доверительные интервалы изначально были созданы для того, чтобы оценивать вероятность того, что гипотеза подтверждается статистикой, а не для рейтинга. Доверительные интервалы очень сильно зависят от необходимой вероятности и принцип ее выбора непонятен из статьи.
Более того автор пытается ее применять для 5ти бальной оценки, хотя эта формула описывает только распределение с двумя вариантам. Для этих целей есть другие формулы. Если на сайте есть рейтинг с плюсом и минусом, то это тоже не двух вариантное распределение. В фильме, было именно два варианта — у пользователя была только возможность проголосовать за одну из двух девушек, а вероятность закрытия страницы значительно ниже, чем голосования.
В итоге нам предлагают сортировать по оценке (с точностью до наугад выбранного параметра) нижней границы вероятности того, что пользователь поставит +, если он все-таки проголосует.
Богатые богатеют
Если пользователям по умолчанию показываются статьи с самым высоким рейтингом и этот рейтинг зависит от числа оценок, то мы имеем положительный обратный эффект. Старые статьи выше в рейтинге, они получают больше посетителей, им ставят больше оценок в итоге они еще больше отрываются от молодых статей.
Даже если все статьи добавлены единовременно, то из-за случайной оценки несколько случайных статей взлетит на вверх и получит больше голосов и опять начнется цепная реакция.
Если рейтинг сильно влияет на число посещений страницы, то либо используйте и положительные и отрицательные оценки, чтобы добросовестные пользователи чистили «топ», либо не используйте количество оценок как параметр сортировки ни в каком виде, а чтобы избежать недостоверных статей вверху рейтинга — исключите из поиска статьи с меньшим определенного числом голосов как на AG.ru.
Плюс/минус
Основное преимущество таких типов рейтингов для положительных статей рейтинг итак зависит от числа проголосовавших и вверху не будет статей с одним случайным голосом. Более того, рейтинг хороших статей распределяется близко к биномиальному распределению, поведение которого и моделирует «формула на стекле».
Плюс/минус хороший вариант рейтинга. В топе не будет и плохих статей и непроверенных. Он интуитивно понятнее для пользователей, чем какое-то математическое моделирование и очень просто организуется. Вариант только с плюсом хуже, поскольку пользователь, увидев плохую статью, не может никак повлиять на ее позицию.
«Пять звезд»
Вот с эти рейтингом и получаются проблемы, когда благодаря одному голосу рейтинг какой-то статьи не оправдано высок. Самый простой способ избежать этого исключить из рейтинга статьи с малым числом голосов.
Если вы не хотите исключать статьи с малым числом голосов — то существует множество решений данной проблемы, однако, точного ответа какой из них можно использовать — нет. Приведу самый простой из них.
Мат. ожидание рейтинга (наиболее вероятное значение рейтинга статьи после бесконечного числа голосований) для статьи за которую еще никто не голосовал равно среднему рейтингу всех статей сайта.
Мат. ожидание рейтинга статьи, за которую уже голосовали, будет где-то между средним рейтингом всех статей и средним рейтингом этой статьи. Причем, с увеличением числа голосов рейтинг должен все больше учитывать рейтинг самой статьи, чем средний рейтинг. Самая простая формула которая это реализует это Среднее арифметическое взвешенное по числу голосов среднестатистической статьи и текущей:

Где R средний рейтинг всех статей, N среднее число голосов. Ri средний рейтинг этой статьи, Ni число голосов этой статьи. R и N можно подставить константами — они слабо меняются со временем.
В формулу можно добавить настройку консерватизма:

K>0. Чем меньше K, тем легче новой статье пробиться на вверх в выдаче. Чем он выше, тем сортировка будет стабильнее и тем сильнее будет эффект «богатые богатеют». При K=0 сортировка сводится к самому простому варианту.
Комбинированный рейтинг
Как уже говорилось, что основная наша проблема в том, что если у какой-то статьи (или товара) всего одна оценка в 5 балов, то его рейтинг будет выше чем у статьи с сотней голосов в пять балов и одним в 4ре бала. Другими словами голоса имеют разный вес. Единственный простой рейтинг, который лишен это недостатка это плюс/минус. Однако, звездочки более привычны пользователям их можно засунуть в выдачу Яндекса и Гугла и они позволяют судить пользователям насколько хорош товар (4 звезды более понятно, чем +40).
Поэтому, можно соединить два варианта: выводить «звездочки» пользователям, но сортировать по плюсам и минусам. Голос увеличивает оценку статьи 1, если он выше, скажем, 3, либо уменьшает на 1, если ниже. Можно немного усложнить: голос увеличивает оценку на число балов поставленных пользователем минус средний рейтинг статей(R — Ri).
Однако, в этом случае, консерватизм рейтинга и эффект «богатые богатеют» будет выше, чем варианте со среднезвешанным.
Автор: Hkey