3D своими руками. Часть 2: оно трехмерное

В предыдущей части мы разобрались, как выводить на экран двумерные объекты, такие как пиксель и линия (отрезок), но ведь хочется поскорее создать что-то трехмерное. В этой статье впервые попробуем вывести 3D-объект на экран и познакомимся с новыми математическими объектами, такими как вектор и матрица, а также некоторыми операциями над ними, но только с теми, которые применим на практике.

Во второй части мы рассмотрим:

• Системы координат
• Точка и вектор
• Матрица
• Вершины и индексы
• Конвейер визуализации

Системы координат

Хочется отметить, что некоторые примеры и операции в статьях изложены неточно и сильно упрощены для улучшения понимания материала, ухватив суть, вы сможете самостоятельно найти лучшее решение или исправить ошибки и неточности в демонстрационном коде. Перед тем как нарисуем что-то трехмерное, важно помнить, что все трехмерное на экране выводится двухмерными пикселями. Для того, чтобы объекты нарисованные пикселями выглядели трехмерными, нам необходимо разобрать немного математики. Мы не будем не будем рассматривать формулы и объекты, не видя их применения. Именно поэтому, все математические операции, которые вы встретите в данной статье, будут применены на практике, что упростит их понимание. 

Первое что необходимо разобрать – это системы координат. Посмотрим, какие системы координат используются, а также выберем, какую использовать нам.

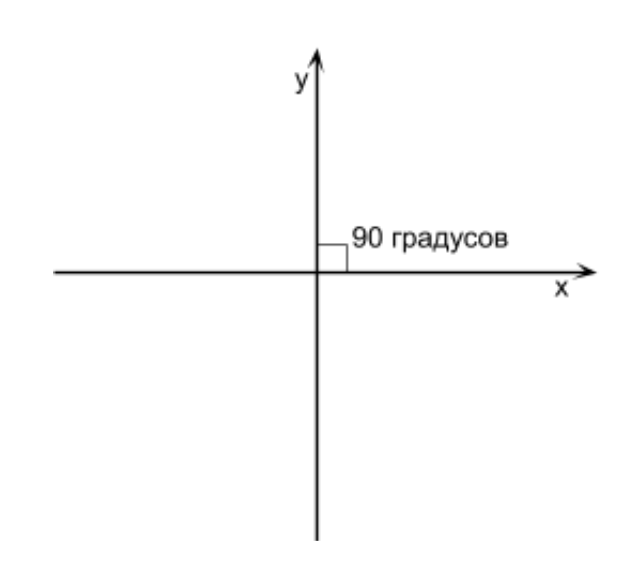
Что такое система координат? Это способ определять положение точки или персонажа игры состоящего из точек при помощи чисел. Система координат имеет 2 направления осей (будем их обозначать как X, Y), если мы работаем с 2D графикой. Если мы 2D-объекту зададим больший Y и он станет выше, чем был до этого – это значит, что ось Y направлена вверх. Если мы объекту зададим больший Х и он станет правее – это  значит, что ось Х направлена вправо. Это и есть направления осей, а вместе они называются системой координат. Если в месте пересечения осей Х и Y образуется угол 90 градусов, то такую систему координат называют прямоугольной (еще называют Декартовой системой координат) (см. Рисунок выше).

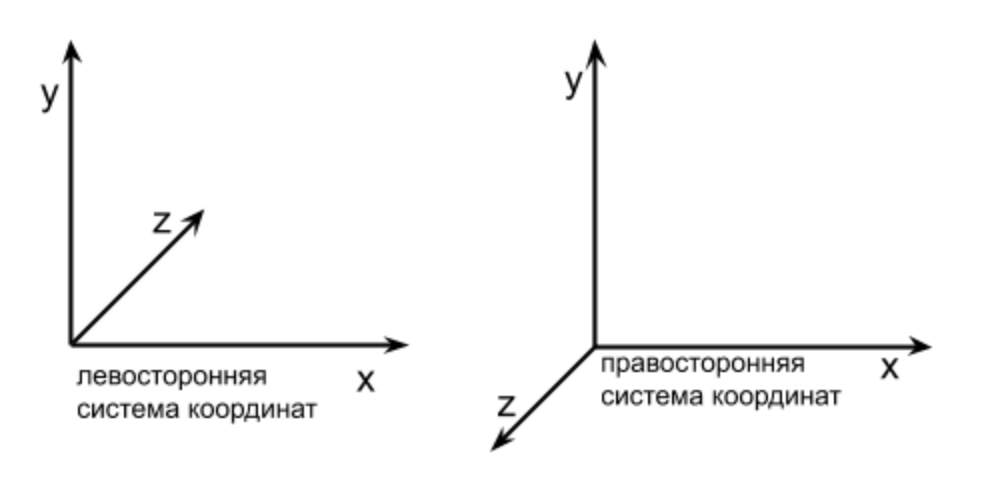
Но это была система координат в 2D мире, в трехмерном же, появляется еще одна ось – Z. Если ось Y (еще говорят ордината) позволяет рисовать выше/ниже, ось Х (еще говорят абсцисса) левее/правее, то ось Z (еще говорят аппликата) позволяет отдалять/приближать объекты. В трехмерной графике часто (но не всегда) используется система координат, в которой ось Y направлена вверх, ось Х направлена вправо, а вот Z может быть направлена, либо в одном направление, либо в другом. Именно поэтому системы координат мы разделим на 2 типа – левостороннюю и правостороннюю (см. Рисунок выше).

Как видно из рисунка, левосторонней системой координат (еще говорят левая система координат) называют когда ось Z, направлена от нас (чем больше Z, тем дальше объект), если же ось Z направлена к нам, то это – правосторонняя система координат (еще говорят правая система координат). Почему их так назвали? Левая, потому что, если левую руку направить ладонью вверх, а пальцами в сторону оси Х, то большой палец укажет направление Z, то есть, будет направлен в сторону монитора, если Х направлен вправо. Тоже проделайте с правой рукой, и ось Z будет направлена от монитора, при Х вправо. Запутались с пальцами? В интернете есть разные способы ставить руку и пальцы, чтобы получить нужные направления осей, но это не обязательная часть.

Для работы с 3D-графикой есть много библиотек для разные языков, где используются разные системы координат. Например, в библиотеке Direct3D используется левосторонняя система координат, а в OpenGL и WebGL правосторонняя, в VulkanAPI ось Y направлена вниз (чем меньше Y тем выше будет объект) а Z от нас, но это всего лишь соглашения, в библиотеках мы можем сами указать ту систему координат, которую считаем более удобной.

Какую систему координат выбрать нам? Подойдет любая, мы только учимся и направления осей сейчас на усвоение материала не повлияют. В примерах мы будем использовать правостороннюю систему координат и чем меньше мы укажем Z для точки, тем дальше она будет от экрана, при этом X,Y будут направлены вправо/вверх.

Точка и вектор

Теперь вы базово знаете, что такое системы координат и какие есть направления осей. Далее необходимо разобрать, что такое точка и вектор, т.к. они нам понадобятся в этой статье для практики. Точкой в 3D-пространстве называют какое-то местоположение, заданное через [X, Y, Z]. Например, мы своего персонажа хотим разместить в самом начале координат (возможно, в центре окна), тогда его положение будет [0, 0, 0], или же можно сказать, что он расположен в точке [0, 0, 0]. Теперь, мы хотим разместить противника левее игрока на 20 единиц (к примеру, пикселей),  значит, он будет расположен в точке [-20, 0, 0]. Мы постоянно будем работать с точками, поэтому подробнее их разберем позже. 

Что такое вектор? Это направление. В 3D-пространстве оно описывается, как и точка, 3-мя значениями [X, Y, Z]. Например, нам необходимо передвигать персонажа вверх на 5 единиц каждую секунду, значить мы будем менять Y, добавляя к нему каждую секунду 5, но X и Z трогать не будем, такое перемещение можно записать в виде вектора [0, 5, 0]. Если же наш персонаж постоянно двигается вниз на 2 единицы и вправо на 1, то вектор его перемещения будет выглядеть так: [1, -2, 0]. Мы написали -2 т.к. Y вниз уменьшается.

У вектора нет положения, а [X, Y, Z] обозначают направление. Вектор можно прибавлять к точке, для того, чтобы получить новую точку, смещенную на вектор. Например, выше я уже упомянул, что если мы хотим двигать 3D-объект (например, игрового персонажа) каждую секунду на 5 единиц вверх, то вектор смещения будет таким: [0, 5, 0]. Но как его использовать для перемещения? 

Допустим, персонаж находится в точке [5, 7, 0], а вектор смещения [0, 5, 0]. Если мы прибавим к точке вектор, то получим новое положение игрока. Складывать точку с вектором, или вектор с вектором можно по следующему правилу.

Пример сложения точки и вектора:

[5, 7, 0] + [0, 5, 0] = [5 + 0, 7 + 5, 0 + 0] = [5, 12, 0] – это и есть новое положения нашего персонажа. 

Как видим, наш персонаж передвинулся на 5 единиц вверх, отсюда появляется новое понятие – длина вектора. У каждого вектора она есть, кроме вектора [0, 0, 0], который называют нулевым вектором, такой вектор также не имеет направления. У вектора [0, 5, 0]  длина равна 5, т.к. такой вектор смещает точку на 5 единиц вверх. У вектора [0, 0, 10] длина 10, т.к. он может сместить точку на 10 по оси Z. Но вот у вектора [12, 3, -4] «на глаз» и не скажешь какая длина, поэтому будем использовать формулу вычисления длины вектора. Возникает вопрос, зачем нам длина вектора? Одно и применений – узнать на какое расстояние переместится персонаж или чтобы сверить скорости персонажей, у кого длина вектора смещения больше, тот и быстрее. Длина также используется для кое-каких операций над векторами. Длину вектора можно вычислить по следующей формуле из первой части (только добавился Z):

Давайте посчитаем по формуле выше длину вектора [6, 3, -8];

Длина вектора [6, 3, -8] приблизительно равна 10.44.

Мы уже знаем, что такое точка, вектор, как суммировать точку и вектор (или 2 вектора), и как вычислять длину вектора. Давайте добавим класс вектора и реализуем в нем суммирование и вычисление длины. Хочу также обратить внимание на то, что мы не будем создавать класс для точки, если нам понадобится точка, то мы будем использовать класс вектора, т.к. и точка и вектор хранят в себе X, Y, Z,  просто для точки это положение, а для вектора направление.

Добавьте в проект с предыдущей статьи класс вектора, можно его добавить ниже класса Drawer. Я свой класс назвал Vector и добавил в него 3 свойства X, Y, Z:

class Vector {
  x = 0;
  y = 0;
  z = 0;

  constructor(x, y, z) {
    this.x = x;
    this.y = y;
    this.z = z;
  }
}

Заметьте, что поля x, y, z  без функций «аксессоров», так мы можем напрямую обращаться к данным в объекте, это сделано для более быстрого доступа. Позднее, мы оптимизируем этот код еще сильнее, но сейчас оставим так, чтобы улучшить читаемость.

Теперь реализуем суммирование векторов. Функция будет принимать 2 суммируемых вектора, поэтому я думаю сделать ее статической. Тело функции будет работать согласно формуле выше. Результатом нашего суммирования получится новый вектор, которым мы и будем возвращать:

static add(v1, v2) {
    return new Vector(
        v1.x + v2.x,
        v1.y + v2.y,
        v1.z + v2.z,
    );
}

Осталось реализовать функцию вычисления длины вектора. Опять же, все реализовываем по формулам, которые были выше:

getLength() {
    return Math.sqrt(
        this.x * this.x + this.y * this.y + this.z * this.z
    );
}

Теперь посмотрим на еще одну операцию над вектором, которая понадобится немного позже в этой и много в последующих статьях – «нормализация вектора». Допустим, у нас в игре есть персонаж, которого мы перемещаем клавишами стрелок. Если нажимаем вверх, то он перемещается на вектор [0, 1, 0], если вниз то [0, -1, 0], влево [-1, 0, 0] и вправо [1, 0, 0]. Здесь хорошо видно, что длины каждого из векторов равны 1, то есть, скорость персонажа равна 1. А давайте добавим перемещение по диагонали, если игрок зажимает стрелочку вверх и вправо, то какой будет вектор смещения? Самый очевидный вариант это вектор [1, 1, 0]. Но если посчитаем его длину, то увидим, что она приблизительно равна 1.414. Получается, что наш персонаж по диагонали будет ходить быстрее? Такой вариант не годится, но чтобы наш персонаж ходил по диагонали со скоростью 1, вектор должен быть: [0.707, 0.707, 0]. Откуда я взял такой вектор? Я взял вектор [1, 1, 0] и нормализовал его, после чего получил [0.707, 0.707, 0]. То есть, нормализация – это приведение вектора к длине 1 (единичной длине) без изменения его направления. Заметьте, что векторы [0.707, 0.707, 0] и [1, 1, 0] указывают в одном направлении, то есть персонаж будет в обоих случаях двигаться строго вверх вправо, но вектор [0.707, 0.707, 0] является нормализованным и скорость персонажа теперь будет равно 1, что исключит баг с ускоренным перемещением по диагонали. Рекомендуется всегда перед любыми вычислениями нормализовать вектор во избежание различного рода ошибок. Давайте посмотрим, как нормализовать вектор. Нужно разделить каждую его компоненту (X, Y, Z) на его длину. Функция нахождения длины уже есть, половина дела сделана, теперь напишем функцию нормализации вектора (внутри класса Vector):

normalize() {
    const length = this.getLength();
    
    this.x /= length;
    this.y /= length;
    this.z /= length;
    
    return this;
}

Метод normalize нормализует вектор и возвращает его (this), это нужно чтобы в дальнейшем можно было normalize использовать в выражениях.

Теперь, когда мы знаем что такое нормализация вектора, и знаем что ее лучше выполнять перед использованием вектора, возникает вопрос. Если нормализация вектора – это приведение к единичной длине, то есть скорость перемещения объекта (персонажа) будет равна 1, то как ускорить персонаж? Например, при перемещении персонажа по диагонали вверх/вправо со скоростью 1, его вектор будет [0.707, 0.707, 0], а какой вектор будет если мы захотим персонажа перемещать в 6 раз быстрее? Для этого существует операция, которая называется «умножение вектора на скаляр». Скаляром называют обычное число на которое умножают вектор. Если скаляр будет равен 6, то вектор станет в 6 раз длиннее, а наш персонаж в 6 раз быстрее соответственно. Как же выполнить умножение на скаляр? Для этого необходимо умножить каждую компоненту вектора на скаляр. Например, решим задачу выше, когда персонажа перемещающегося на вектор [0.707, 0.707, 0] (скорость 1) необходимо ускорить в 6 раз, то есть умножить вектор на скаляр 6. Формула умножения вектора «V» на  скаляр «s» следующая:

В нашем случае это будет:
– новый вектор перемещения, длина которого равна 6.

Важно знать, что положительный скаляр масштабирует вектор не меняя его направления, если же скаляр отрицательный, то он также масштабирует вектор (увеличивает его длину) но вдобавок меняет направление вектора на противоположное.

Давайте реализуем функцию multiplyByScalar умножения вектора на скаляр в нашем классе Vector:

multiplyByScalar(s) {
    this.x *= s;
    this.y *= s;
    this.z *= s;
    
    return this;
}

Матрица

Мы немного разобрались с векторами и некоторыми операциями над ними, которые понадобятся в этой статье. Далее необходимо разобраться с матрицами.

Можно сказать, что матрица – это самый обычный двумерный массив. Просто в программирования используют термин «двумерный массив», а в математике «матрица». Для чего же в 3D-программировании нужны матрицы? Это мы разберем, как только немного научимся с ними работать. 

Мы будем использовать только числовые матрицы (массив чисел). У каждой матрицы есть свой размер (как у любого 2-мерного массива). Вот несколько примеров матриц:

Из всех операций над матрицами, мы сейчас рассмотрим лишь умножение (остальные позже). Так получается, что умножение матриц не самая простая операция, она способна легко запутать, если не внимательно проследить за порядком умножения. Но не переживайте, у вас все получится, т.к. тут мы будем только умножать и суммировать. Для начала, нужно запомнить пару особенностей умножения, которые нам понадобятся:

• Если мы пытаемся умножить число A на число B, то это ведь то же самое, что и B * A. Если мы переставляем, при каком либо действии операнды и результат не меняется, то говорят, что операция коммутативна. Пример:  a + b = b + a операция коммутативна, a – b ≠ b – a операция некоммутативна, a * b = b * a операция умножения чисел – коммутативна. Так вот, операция умножения матриц некоммутативна в отличии от умножения чисел. То есть, умножение матрицы M на матрицу N не будет равно умножению матрицы N на M.
• Умножение матриц возможно, если количество столбцов первой матрицы (которая слева) равняется количеству строк второй матрицы (которая справа). 

Теперь еще немного разберемся со второй особенностью умножения матриц (когда возможно умножение). Вот несколько примеров, которые демонстрируют когда умножение возможно, а когда нет:

Думаю, данные примеры немного разъяснили картину, когда возможно умножение. Результатом умножения матриц, будет всегда матрица, количество строк которой будет равно количеству строк 1-й матрицы, а количество столбцов, равно количеству столбцов 2-й. Например, если умножить матрицу 2 на 6 и 6 на 8, то получится матрица размером 2 на 8. Теперь перейдем, непосредственно к самому умножению.

Для умножения важно помнить, что столбцы и строки в матрице нумеруются начиная с 1, а в массиве с 0. Первый индекс в элементе матрицы, указывает на номер строки, а второй на номер столбца. То есть, если элемент матрицы (элемент массива) записан в виде: m28, это значит что мы обращаемся ко второй строке и восьмому столбцу. Но поскольку в коде мы будем работать с массивами, вся индексация строк и столбцов у нас будет начинаться с 0.

Давайте попробуем перемножить 2 матрицы A и B с конкретными размерами и элементами:

Видно, что матрица А имеет размер 3 на 2, а матрица В размер 2 на 2, умножение возможно:

Как видим, у нас получилась матрица 3 на 2, умножение поначалу запутанное, но если есть цель научиться умножать «без напряга», необходимо решить несколько примеров. Вот еще пример умножения матриц A и В:

Если не до конца понятно умножение – ничего страшного, т.к. умножать на листике нам не придется. Мы напишем один раз функцию умножения матриц и будем использовать её. Вообще, все эти функции уже написаны, но мы делаем все самостоятельно.

Теперь еще немного терминов, которые будут в дальнейшем использоваться:

• Квадратной матрицей называется матрица, в которой количество строк равно количеству столбцов, вот пример квадратных матриц:

• Главной диагональю квадратной матрицы называют все элементы матрицы, у которой номер строки равен номеру столбца. Примеры диагоналей (в этом примере главная диагональ заполнена девятками): 

• Единичной матрицей называют квадратную матрицу, у которой все элементы главной диагонали равны 1, а все остальные равны 0. Примеры единичных матриц:

Еще важно запомнить такое свойство, что если умножить любую матрицу M на  подходящую по размеру единичную матрицу, к примеру назовем ее I, то получим исходную матрицу M, например:  M * I = M или I * M = M. Т.е. умножение матрицы на единичную матрицу никак не влияет на результат. К единичной матрице мы вернемся позднее. В 3D-программировании мы часто будем использовать квадратную матрицу 4 на 4.

Теперь немного разберем, зачем нам нужны будут матрицы и зачем их умножать? В 3D-программировании существует множество различных матриц 4 на 4, которые если умножить на вектор или точку, будут выполнять нужные нам действия. Например, нам необходимо повернуть персонажа в трехмерном пространстве вокруг оси Х, как это сделать? Умножить вектор на специальную матрицу, которая отвечает за поворот вокруг оси X. Если нужно переместить и повернуть точку вокруг начала координат, то нужно умножить эту точку на специальную матрицу. У матриц есть прекрасное свойство – комбинирования преобразований (рассмотрим в этой статье). Допустим, нам необходимо персонажа состоящего из 100 точек (вершин, но об этом тоже будет немного ниже) в приложении увеличить в 5 раз, потом повернуть на 90 градусов по Х, потом перенести на 30 единиц вверх. Как уже было сказано – для разных действий уже существуют специальные матрицы, которые мы рассмотрим. Для выполнения задачи выше, мы, к примеру, в цикле перебираем все 100 точек и каждую сначала умножаем на 1-ю матрицу, чтобы увеличить персонажа, затем умножаем на 2-ю матрицу, чтобы повернуть на 90 градусов по Х, потом умножаем на 3-ю для перемещения на 30 единиц вверх. Итого, для каждой точки у нас 3 умножения матрицы, а точек 100, значит, умножений будет 300. Но если мы возьмем и перемножим между собой матрицы для увеличения в 5-ть раз, поворота на 90 градусов по Х и перемещение на 30 ед. вверх, то получим матрицу, которая в себе содержит все эти действия. Умножив точку на такую матрицу, точка окажется там, где нужно. Подсчитаем теперь, сколько действий выполняется: 2 умножения для 3-х матриц, и 100 умножений для 100 точек, итого 102 умножения – точно лучше, чем 300 умножений до этого. Тот момент, когда мы перемножили 3 матрицы для объединения различных действий в одну матрицу – называется комбинированием преобразований и мы его обязательно сделаем на примере.

Как умножить матрицу на матрицу мы разбирали, но в прочитанном выше абзаце говорится об умножении матрицы на точку или вектор. Для умножения точки или вектора достаточно их представить матрицей.

Например, у нас есть вектор [10, 2, 5] и есть матрица: 

Видно, что вектор можно представить матрицей 1 на 3 или матрицей 3 на 1. Поэтому мы можем умножить вектор на матрицу 2 способами:

Как видно, мы можем представить вектор как вектор-строку и умножать его на матрицу, или представить вектор, как вектор-столбец и умножать матрицу на него. Давайте проверим, будет ли результат умножения одинаковым в обоих случаях:

Умножаем вектор-строку на матрицу:

Теперь, умножим матрицу на вектор-столбец:

Мы видим, что умножая вектор-строку на матрицу и матрицу на вектор-столбец, мы получили совершенно разные результаты (вспоминаем про коммутативность). Поэтому, в 3D-программировании существую матрицы, которые предназначены для умножения только на вектор строку, или только на вектор столбец. Если мы умножим матрицу предназначенную для вектора-строки на вектор-столбец, то получим результат, который нам ничего не даст. Используйте удобное вам представление вектора/точки (строка или столбец), только в дальнейшем используйте для вашего представления вектора/точки соответствующие матрицы. В Direct3D, например, используют строковое представление векторов, и все матрицы в Direct3D предназначение для умножения вектора-строки на матрицу. В OpenGL используется представление вектора (или точки), как столбца, и все матрицы предназначены для умножения матрицы на вектор-столбец. В статьях будем использовать вектор-столбец и будем умножать, матрицу на вектор-столбец.

Подведем небольшой итог прочитанного про матрицы.

• Для выполнения действия над вектором (или точкой) существуют специальные матрицы, некоторые из которых мы посмотрим в этой статье.
• Для объединения преобразования (перемещения, вращения и т.д.) мы можем перемножить матрицы каждого преобразования между собой и получим матрицу, которая содержит все преобразования вместе.
• В 3D-программировании мы постоянно будем использовать квадратные матрицы 4 на 4.
• Мы можем умножать матрицу на вектор (или точку) представив его, как столбец или строку. Но для вектора-столбца и вектора-строки нужно использовать разные матрицы.

После небольшого разбора матриц, давайте добавим класс матрицы 4 на 4 и реализуем методы умножения матрицы на матрицу, и вектора на матрицу. Мы будем использовать размер матрицы 4 на 4, т.к. все стандартные матрицы, которые используются для различных действий (перемещение, вращения, масштаб, …) имеют такой размер, матрицы другого размера нам не понадобятся.  

Давайте добавим в проект класс Matrix. Еще иногда класс для работы с матрицами 4 на 4 называют Matrix4, и эта 4 в названии говорит нам о размере матрицы (еще говорят матрица 4-го порядка). Все данные матриц мы будем хранить в двумерном массиве 4 на 4.

Перейдем к реализации операций умножения. Я не рекомендую использовать циклы для этого. Чтобы повысить быстродействие, мы все должны умножать построчно – так получится сделать за счет того, что все умножения у нас будут происходить с матрицами фиксированного размера.  Я буду использовать циклы для операции умножения, только для экономии объема кода, вы же можете написать все умножение без циклов вообще. У меня код умножения выглядит так:

class Matrix {
  static multiply(a, b) {
    const m = [
      [0, 0, 0, 0],
      [0, 0, 0, 0],
      [0, 0, 0, 0],
      [0, 0, 0, 0],
    ];

    for (let i = 0; i < 4; i++) {
      for (let j = 0; j < 4; j++) {
        m[i][j] = a[i][0] * b[0][j] +
          a[i][1] * b[1][j] +
          a[i][2] * b[2][j] +
          a[i][3] * b[3][j];
      }
    }

    return m;
  }
}

Как видите, метод принимает матрицы a и b, умножает их и возвращает результат в виде такого же массива 4 на 4. В начале метода я создал матрицу m заполненную нулями, но это не обязательно, так я хотел показать какой размерности будет результат, вы же можете создать массив 4 на 4, без каких либо данных.

Теперь необходимо реализовать умножение матрицы на вектор-столбец, как обсудили выше. Но если представить вектор столбцом, то получится матрица вида:
на которую нам нужно будет умножать на матрицы 4 на 4 для выполнения различных действий. Но на этом примере прекрасно видно, что такое умножение выполнить нельзя, ведь у вектора-столбца 3 строки, а у матрицы 4 столбца. Что же тогда делать? Нужен какой-то четвертый элемент, тогда у вектора станет 4 строки, которые будут равны количеству столбцов у матрицы. Давайте добавим вектору такой 4-й параметр и назовем его W, теперь у нас все вектора в 3D будут вида [X, Y, Z, W] и такие вектора уже можно будет умножать на матрицу 4 на 4. На самом деле у компоненты W более глубокое назначение, но с ним мы познакомимся в следующей части (ведь не зря у нас матрица 4 на 4, а не 3 на 3).  Добавляем в класс Vector, который мы создавали выше компоненту w. Теперь начало класса Vector выглядит так:

class Vector {
    x = 0;
    y = 0;
    z = 0;
    w = 1;

    constructor(x, y, z, w = 1) {
        this.x = x;
        this.y = y;
        this.z = z;
        this.w = w;
    }

Я проинициализировал W единицей, но почему 1? Если мы присмотримся к тому, как умножаются компоненты матрицы и вектора (пример кода ниже), можно заметить, что если поставить в качестве W значение 0 или любое другое отличное от 1, тогда при умножении этот W будет влиять на результат, а мы пока не знаем, как им пользоваться, а если мы его сделаем 1, то он в векторе будет, но результат никак не поменяет. 

Теперь вернемся к матрице и реализуем в классе Matrix (можно и в классе Vector, разницы нет) умножения матрицы на вектор, которое уже возможно, благодаря W:

static multiplyVector(m, v) {
  return new Vector(
    m[0][0] * v.x + m[0][1] * v.y + m[0][2] * v.z + m[0][3] * v.w,
    m[1][0] * v.x + m[1][1] * v.y + m[1][2] * v.z + m[1][3] * v.w,
    m[2][0] * v.x + m[2][1] * v.y + m[2][2] * v.z + m[2][3] * v.w,
    m[3][0] * v.x + m[3][1] * v.y + m[3][2] * v.z + m[3][3] * v.w,
  )
}

Обратите внимание, что матрицу мы представили массивом 4 на 4, а вектор объектом со свойствами x, y, z, w, в будущем мы вектор поменяем и он тоже будет представлен массивом 1 на 4, т.к. это ускорит умножение. Но сейчас, для того чтобы лучше видеть, как происходит умножение и улучшить понимание кода, мы менять вектор не будем.

Код для умножения матриц между собой и умножения матрицы на вектор мы написали, но все еще не понятно как это нам поможет в трехмерной графике.

Хочу также напомнить, что я вектором называю как точку (положение в пространстве) так и направление, т.к. оба объекта содержат одинаковую структуру данных x, y, z и нововведенный w. 

Давайте рассмотрим некоторые из матриц, которые выполняют базовые операции над векторами. Первой из таких матриц будет матрица перемещения (Translation matrix). Умножив матрицу перемещения на вектор (местоположение) он сместится на указанное число единиц в пространстве. А вот и матрица перемещения:

Где dx, dy, dz означают смещения по осям x,y,z соответственно, эта матрица предназначена для умножения на вектор-столбец. Такие матрицы можно найти в интернете или в любой литературе по 3D-программированию, нам не нужно их создавать самим, воспринимайте их сейчас, как формулы, которыми вы пользуетесь со школы, которые просто нужно знать или понимать для чего их использовать.  Давайте проверим действительно ли умножив такую матрицу на вектор произойдет смещение. Возьмем в качестве вектора, который мы собираемся перемещать вектор [10, 10, 10, 1] (4-й параметр W всегда оставляем 1) предположим, что это положение нашего персонажа в игре и мы хотим его сместить на 10 единиц вверх, 5 единиц вправо, и на 1 единицу отдалить от экрана. Тогда вектор смещения будет таким [10, 5, -1] ( -1 потому что у нас правосторонняя система координат и чем дальше Z, тем он меньше). Если мы посчитаем результат без матриц, обычным суммированием векторов. То получится такой результат: [10 + 10, 10 + 5, 10 + -1, 1] = [20, 15, 9, 1] – это новые координаты нашего персонажа. Умножив матрицу выше на начальные координаты [10, 10, 10, 1], мы должны получить такой же результат, давайте проверим это в коде, напишем умножение после классов Drawer, Vector и Matrix:

const translationMatrix = [
  [1, 0, 0, 10],
  [0, 1, 0, 5],
  [0, 0, 1, -1],
  [0, 0, 0, 1],
]
        
const characterPosition = new Vector(10, 10, 10)
        
const newCharacterPosition = Matrix.multiplyVector(
  translationMatrix, characterPosition
)
console.log(newCharacterPosition)

В этом примере, в матрицу перемещения мы подставили нужное смещение персонажа (translationMatrix), проинициализировали его начальное положение (characterPosition) и потом перемножили его с матрицей, а результат вывели через console.log (это отладочный вывод в JS). Если вы используете не JS, то выведите X, Y, Z самостоятельно при помощи инструментов вашего языка. Результат, который мы получили в консоли: [20, 15, 9, 1], все сходится с результатом, который мы посчитали выше. У вас может возникнуть вопрос, зачем получать такой же результат умножением вектора на специальную матрицу, если мы его гораздо проще получили просуммировав вектор со смещением покомпонентно. Ответ не самый простой и мы подробнее его еще обсудим, но сейчас можно отметить что как обсуждалось ранее, мы матрицы с разными преобразованиями можем комбинировать между собой, таким образом сокращая очень много вычислений. Матрицу translationMatrix в примере выше, мы создали в виде массива вручную и подставили туда необходимое смещение, но поскольку мы этой и другими матрицами будем пользоваться часто, то давайте вынесем ее в метод в классе Matrix, и смещение в нее будем передавать аргументами:

static getTranslation(dx, dy, dz) {
  return [
    [1, 0, 0, dx],
    [0, 1, 0, dy],
    [0, 0, 1, dz],
    [0, 0, 0, 1],
  ]
}

Присмотритесь еще раз к матрице перемещения, вы увидите, что dx, dy, dz находятся в последнем столбце и если мы посмотрим код умножения матрицы на вектор, то заметим, что именно этот столбец умножается на W компоненту вектора. И если бы она была, например 0, то dx, dy, dz, мы бы умножали на 0 и перемещение не работало бы. Но мы можем W делать равное 0, если мы хотим в классе Vector хранить направление, т.к. направление перемещать нельзя, то так бы мы обезопасили себя, и даже если мы умножим такое направление на матрицу перемещения, то это никак не поломает вектор направления, т.к. все перемещение будем умножаться на 0.

Итого можем применить такое правило, местоположение мы создаем так:

new Vector(x, y, z, 1) // 1 у нас по умолчанию, можно не указывать

А направление создам так:

new Vector(x, y, z, 0)

Так мы сможем отличать местоположение и направление, и при умножении направления на матрицу перемещения мы случайно не сломаем вектор направления.

Вершины и индексы

Прежде чем посмотрим какие еще есть матрицы, разберемся немного с тем, как нам применить уже имеющиеся знания для вывода чего-то трехмерного на экран. Все что мы выводили до этого – линии и пиксели. Но давай теперь при помощи этих инструментов, выведем, например куб. Для того чтобы это сделать нам необходимо разобраться из чего состоит трехмерная модель. Самая основная составляющая любой 3D-модели – это точки (далее будем называть вершины) по которым мы можем ее нарисовать, это, по сути, много векторов местоположений, которые, если мы правильно их соединим между собой линиями,  получим 3D-модель (сетку модели) на экране, она будет без текстуры и без многих других свойств, но всему свое время. Взглянем на куб, который мы хотим вывести, и попробуем понять сколько у него вершин:

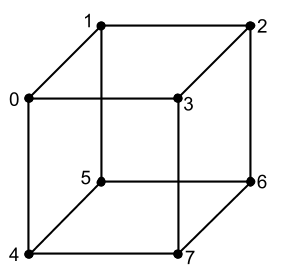
На изображении мы видим, что у куба 8 вершин (для удобства я их пронумеровал). И все вершины между собой соединены линиями (ребра куба). Т.е., чтобы описать куб и нарисовать его линиями, нам нужно 8 координат каждой вершины, и также нужно указать из какой вершины до какой нам рисовать линию, чтобы получился куб, ведь если мы мы неправильно соединим вершины, например проведем линию из вершины 0 в вершину 6, то это точно будет не куб, а другой объект. Давайте сейчас опишем координаты каждой из 8 вершин. В современной графике 3D-модели могут состоять из десятков тысяч вершин, и конечно же никто вручную их не прописывает. Модели рисуют в 3D-редакторах и когда экспортируют 3D-модель, в ее коде уже есть все вершины, нам нужно только их загрузить и нарисовать, но мы пока что учимся и не умеем читать форматы 3D-моделей, поэтому куб опишем вручную, он очень простой.

Представим, что куб выше, находится в центре координат, его середина находится в точке 0, 0, 0 и он должен отображаться вокруг этого центра:

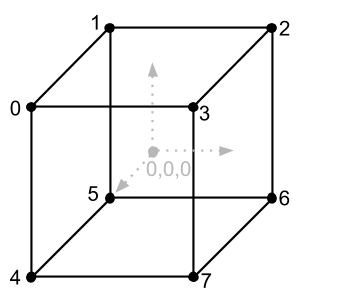
Давайте начнем с вершины 0, и пусть наш куб будет очень маленьким, чтобы не писать сейчас большие значения, размеры моего куба будут 2 в ширину, 2 в высоту и 2 в глубину, т.е. 2 на 2 на 2. На картинке видно, что вершина 0 немного левее центра 0, 0, 0, поэтому я задам X = -1, т.к. чем левее, тем меньше X, также вершина 0 немного выше центра 0, 0, 0, а в нашей системе координат чем выше местоположение, тем больше Y, я задам своей вершине Y = 1, также Z для вершины 0, немного ближе к экрану по отношению к точке 0, 0, 0, поэтому он будет равен Z = 1, ведь в правосторонней системе координат, Z увеличивается с приближением объекта. В итоге мы получили координаты -1, 1, 1 для нулевой вершины, давайте проделаем то же самое для оставшихся 7-ми вершин и сохраним это в массиве, чтобы можно было с ними работать в цикле, у меня получился такой результат (массив можно создать ниже классов Drawer, Vector, Marix):

// Cube vertices
const vertices = [
  new Vector(-1, 1, 1), // 0 вершина
  new Vector(-1, 1, -1), // 1 вершина
  new Vector(1, 1, -1), // 2 вершина
  new Vector(1, 1, 1), // 3 вершина
  new Vector(-1, -1, 1), // 4 вершина
  new Vector(-1, -1, -1), // 5 вершина
  new Vector(1, -1, -1), // 6 вершина
  new Vector(1, -1, 1), // 7 вершина
];

Каждую вершину я положил в экземпляр класса Vector, это не лучший вариант для производительности (лучше в массиве), но сейчас наша цель разобраться как все работает.

Давайте сейчас воспринимать значения координат вершин куба как пиксели, которые мы будем рисовать на экране, в таком случае мы видим что размер куба 2 на 2 на 2 пикселей. Мы создали такой маленький куб, чтобы в т.ч. посмотреть на работу матрицы масштабирования, при помощи которой мы его увеличим. В дальнейшем очень хорошая практика делать модели маленькими, даже еще меньше, чем у нас, чтобы увеличивать их до нужного размера не сильно разными скалярами.

Просто точки куба рисовать пикселями не очень наглядно, т.к. все что мы увидим – это 8 пикселей, по одному на каждую вершину, гораздо лучше нарисовать куб линиями используя функцию drawLine из прошлой статьи. Но для этого нам нужно понять из каких вершин в какие у нас проходят линии. Взглянем на изображение куба с индексами еще раз и мы увидим, что он состоит из 12 линий (или ребер). Также очень легко увидеть что мы знаем координаты начала и конца каждой линии. Например одна из линий (верхняя ближняя) должна быть нарисована из вершины 0 в вершину 3, или же из координат  [-1, 1, 1] в координаты [1, 1, 1]. Информацию о каждой линии нам придется записать в коде вручную смотря на изображение куба, но как правильно это сделать? Если у нас 12 линий и у каждой линии есть начало и конец, т.е. 2 точки, тогда, чтобы нарисовать куб нам понадобится 24 точки? Это правильный ответ, но давайте взглянем на изображение куба еще раз и обратим внимание на то что у куба каждая линия имеет общие вершины, например, в вершине 0 соединяются 3 линии, и так с каждой вершиной. Мы можем сэкономить память и не записывать координаты начала и конца каждой линии, достаточно создать массив и указать индексы вершин из массива vertices в которых эти линии начинаются и заканчиваются. Давайте создадим такой массив и опишем его только индексами вершин, по 2 индекса на каждую линию (начало линии и конец). А немного далее, когда будем рисовать эти линии, мы с легкостью достанем их координаты из массива vertices. Мой массив линий (я назвал его edges, т.к. это ребра куба) я создал ниже массив вершин и выглядит он так:

// Cube edges
const edges = [
  [0, 1],
  [1, 2],
  [2, 3],
  [3, 0],

  [0, 4],
  [1, 5],
  [2, 6],
  [3, 7],

  [4, 5],
  [5, 6],
  [6, 7],
  [7, 4],
];

В этом массиве 12 пар индексов, по 2 индекса вершин на каждую линию.

Давайте сейчас познакомимся еще с одной матрицей, которая увеличит наш куб, и наконец, попробуем его нарисовать на экране. Матрица масштабирования (Scale Matrix) выглядит так:

Параметры sx, sy, sz на главной диагонали означают во сколько раз мы хотим увеличить объект. Если мы в матрицу подставим 10, 10, 10 вместо sx, sy, sz, и умножим эту матрицу на вершины куба, это сделает что наш куб в десять раз больше и он уже будет не 2 на 2 на 2, а 20 на 20 на 20.

Для матрицы масштабирования, так же, как и для матрицы перемещения реализуем метод в классе Matrix, который будет возвращать матрицу с уже подставленными аргументами:

static getScale(sx, sy, sz) {
  return [
    [sx, 0, 0, 0],
    [0, sy, 0, 0],
    [0, 0, sz, 0],
    [0, 0, 0, 1],
  ]
}

Конвейер визуализации

Если мы сейчас попытаемся нарисовать куб линиями используя текущие координаты вершин, то мы получим очень маленький двухпиксельный куб, в верхнем левом углу экрана, т.к. начало координат canvas находится именно там.  Давайте пройдем циклом по всем вершинам куба и умножим их на матрицу масштабирования, чтобы сделать куб больше, а потом еще и на матрицу смещения, чтобы увидеть куб не в верхнем левом углу, а посередине экрана, у меня код перебора вершин с умножением матриц находится ниже массива edges, и выглядит так:

const sceneVertices = []
for(let i = 0 ; i < vertices.length ; i++) {
  let vertex = Matrix.multiplyVector(
    Matrix.getScale(100, 100, 100),
    vertices[i]
  );

  vertex = Matrix.multiplyVector(
    Matrix.getTranslation(400, -300, 0),
    vertex
  );

  sceneVertices.push(vertex);
}

Обратите внимание, что мы не меняем исходные вершины куба, а сохраняем результат умножения в массив sceneVertices, потому что мы можем захотеть нарисовать несколько кубов разных размеров в разных координатах, и если мы будем менять исходные координаты, то следующий куб уже нарисовать не получится, т.к. не из чего будет начинать, начальные координаты будут испорчены первым кубом. В коде выше я увеличил исходный куб в 100 раз по всем направлениям, благодаря умножению всех вершины на матрицу масштабирования с аргументами 100, 100, 100, и также я переместил все вершины куба правее и ниже на 400 и -300 пикселей соответственно, поскольку у нас размеры canvas с прошлой статьи 800 на 600, это как раз будет половина ширины и высоты области рисования, иными словами – центр.

С вершинам мы пока что закончили, но еще нужно все это нарисовать используя drawLine и массив edges, давайте ниже цикла с вершинами напишем еще один цикл для перебора edges и в нем нарисуем все линии:

drawer.clearSurface()

for (let i = 0, l = edges.length ; i < l ; i++) {
  const e = edges[i]

  drawer.drawLine(
    sceneVertices[e[0]].x,
    sceneVertices[e[0]].y,
    sceneVertices[e[1]].x,
    sceneVertices[e[1]].y,
    0, 0, 255
  )
}

ctx.putImageData(imageData, 0, 0)

Вспомним, в прошлой статье все рисование мы начинаем с очистки экрана от предыдущего состояния вызовом метод clearSurface, затем я перебираю все грани куба и рисую куб линиями синего цвета (0, 0, 255), а сами координаты линий я беру из массива sceneVertices, т.к. там лежат уже отмасштабированные и перемещенные вершины в предыдущем цикле, но индексы этих вершин совпадают с индексами оригинальных вершин из массива vertices, т.к. я обрабатывал их и ложил в массив sceneVertices без изменения порядка. 

Если мы сейчас запустим код, то ничего не увидим на экране. Это потому что в нашей системе координат Y смотрит вверх, а в системе координат canvas вниз. Получается,  что наш куб есть, но он находится за пределами экрана и чтобы это исправить, нам нужно перед рисованием пикселя в классе Drawer перевернуть картинку по Y (отзеркалировать). Пока что такого варианта нам будет достаточно, в итоге код рисования пикселя у меня выглядит так:

drawPixel(x, y, r, g, b) {
  const offset = (this.width * -y + x) * 4;

  if (x >= 0 && x < this.width && -y >= 0 && y < this.height) {
    this.surface[offset] = r;
    this.surface[offset + 1] = g;
    this.surface[offset + 2] = b;
    this.surface[offset + 3] = 255;
  }
}

Видно что в формуле получения offset, Y теперь со знаком минус и ось теперь смотрит в нужном нам направлении, также в этом методе я добавил проверку выхода за пределы массива пикселей. В классе Drawer появились и некоторые другие оптимизации благодаря комментариям к предыдущей статье, поэтому выкладываю весь класс Drawer с небольшими оптимизациями и вы можете заменить старый Drawer на этот:

class Drawer {
  surface = null;
  width = 0;
  height = 0;

  constructor(surface, width, height) {
    this.surface = surface;
    this.width = width;
    this.height = height;
  }

  drawPixel(x, y, r, g, b) {
    const offset = (this.width * -y + x) * 4;

    if (x >= 0 && x < this.width && -y >= 0 && y < this.height) {
      this.surface[offset] = r;
      this.surface[offset + 1] = g;
      this.surface[offset + 2] = b;
      this.surface[offset + 3] = 255;
    }
  }

  drawLine(x1, y1, x2, y2, r = 0, g = 0, b = 0) {
    const round = Math.trunc;
    x1 = round(x1);
    y1 = round(y1);
    x2 = round(x2);
    y2 = round(y2);

    const c1 = y2 - y1;
    const c2 = x2 - x1;

    const length = Math.max(
      Math.abs(c1),
      Math.abs(c2)
    );

    const xStep = c2 / length;
    const yStep = c1 / length;

    for (let i = 0 ; i <= length ; i++) {
      this.drawPixel(
        Math.trunc(x1 + xStep * i),
        Math.trunc(y1 + yStep * i),
        r, g, b,
      );
    }
  }

  clearSurface() {
    const surfaceSize = this.width * this.height * 4;
    for (let i = 0; i < surfaceSize; i++) {
      this.surface[i] = 0;
    }
  }
}

const drawer = new Drawer(
  imageData.data,
  imageData.width,
  imageData.height
);

Если сейчас вы запустите код, то на экране будет такое изображение:

Здесь видно, что в центре есть квадрат, хотя мы ожидали получить куб, в чем же дело? На самом деле – это и есть куб, просто он идеально ровно стоит направленным одной из граней (стороной) к нам, поэтому мы не видим его остальных частей. Также мы еще не знакомились с проекциями, и поэтому задняя грань куба не становится меньше с отдалением, как в реальной жизни. Для того, чтобы убедиться, что это действительно куб, давайте его немного повернем, чтобы он был похож на изображение, которое мы видели ранее, когда составляли массив вершин. Для того, чтобы повернуть 3D-изображение, можно использовать 3 специальные матрицы, т.к. поворачивать мы можем вокруг одной из осей X, Y или Z, значит, что для каждой оси, будет своя матрица поворота (Rotation matrix) (есть и другие способы вращения, но это тема следующих статей). Вот как эти матрицы выглядят:

Если мы умножим вершины куба на одну из этих матриц, то куб повернется на указанный угол (a) вокруг той оси, матрицу поворота вокруг которой мы выберем. Тут есть некоторые особенности при повороте вокруг сразу нескольких осей и на них мы посмотрим ниже. Из примера матриц видно, что они используют 2 функции sin и cos и в JavaScript уже есть функционал для их вычисления Math.sin(a) и Math.cos(a), но они работают с радианной мерой углов, которая может показаться не самой удобной, если мы хотим повернуть модель. Мне, например, гораздо удобнее что-то повернуть на 90 градусов (градусная мера), что в радианной мере будет означать Pi / 2 (В JS также есть приблизительное значение Pi это константа Math.PI). Давайте в класс Matrix добавим 3 метода для получения матриц вращения, с принимаемым углом поворота в градусах, который мы преобразуем в радианы, т.к. они нужны для работы функций sin  / cos:

static getRotationX(angle) {
  const rad = Math.PI / 180 * angle;

  return [
    [1, 0, 0, 0],
    [0, Math.cos(rad), -Math.sin(rad), 0],
    [0, Math.sin(rad), Math.cos(rad), 0],
    [0, 0, 0, 1],
  ];
}

static getRotationY(angle) {
  const rad = Math.PI / 180 * angle;

  return [
    [Math.cos(rad), 0, Math.sin(rad), 0],
    [0, 1, 0, 0],
    [-Math.sin(rad), 0, Math.cos(rad), 0],
    [0, 0, 0, 1],
  ];
}

static getRotationZ(angle) {
  const rad = Math.PI / 180 * angle;

  return [
    [Math.cos(rad), -Math.sin(rad), 0, 0],
    [Math.sin(rad), Math.cos(rad), 0, 0],
    [0, 0, 1, 0],
    [0, 0, 0, 1],
  ];
}

Все 3 метода начинаются с преобразования градусов в радианы, после чего мы подставляем угол поворота в радианах в матрицу поворота, передавая углы в функции sin и cos. Почему матрица именно такая, вы можете подробнее прочитать на хабре в тематических статьях, с очень подробным разъяснением, в противном случае – вы можете воспринимать эти матрицы как формулы, которые вычислили для нас и мы можем быть уверенными в том, что они рабочие.

Выше в коде мы реализовали 2 цикла, первый – преобразовывает вершины, второй – выводит линии по индексам вершин, в итоге мы получаем из вершин картинку на экране, и давайте этот участок кода назовем конвейер визуализации. Конвейер потому что мы берем вершину и поочередно делаем с ней разные операции, масштаб, сдвиг, поворот, отрисовку, как на обычном промышленном конвейере. Теперь давайте в первый цикл в конвейере визуализации добавим помимо масштабирования, еще и поворот вокруг осей. Сначала я поверну вокруг X, потом вокруг Y, затем увеличу модель и перемещу ее (2 последних действия уже есть), итого весь код цикла у меня будет таким:

for(let i = 0 ; i < vertices.length ; i++) {
  let vertex = Matrix.multiplyVector(
    Matrix.getRotationX(20),
    vertices[i]
  );

  vertex = Matrix.multiplyVector(
    Matrix.getRotationY(20),
    vertex
  );

  vertex = Matrix.multiplyVector(
    Matrix.getScale(100, 100, 100),
    vertex
  );

  vertex = Matrix.multiplyVector(
    Matrix.getTranslation(400, -300, 0),
    vertex
  );

  sceneVertices.push(vertex);
}

В этом примере я повернул все вершины вокруг оси X на 20 градусов, потом вокруг Y на 20 градусов и 2 оставшихся преобразования у меня уже были. Если вы все сделали правильно, то ваш куб, теперь должен выглядеть трехмерным:

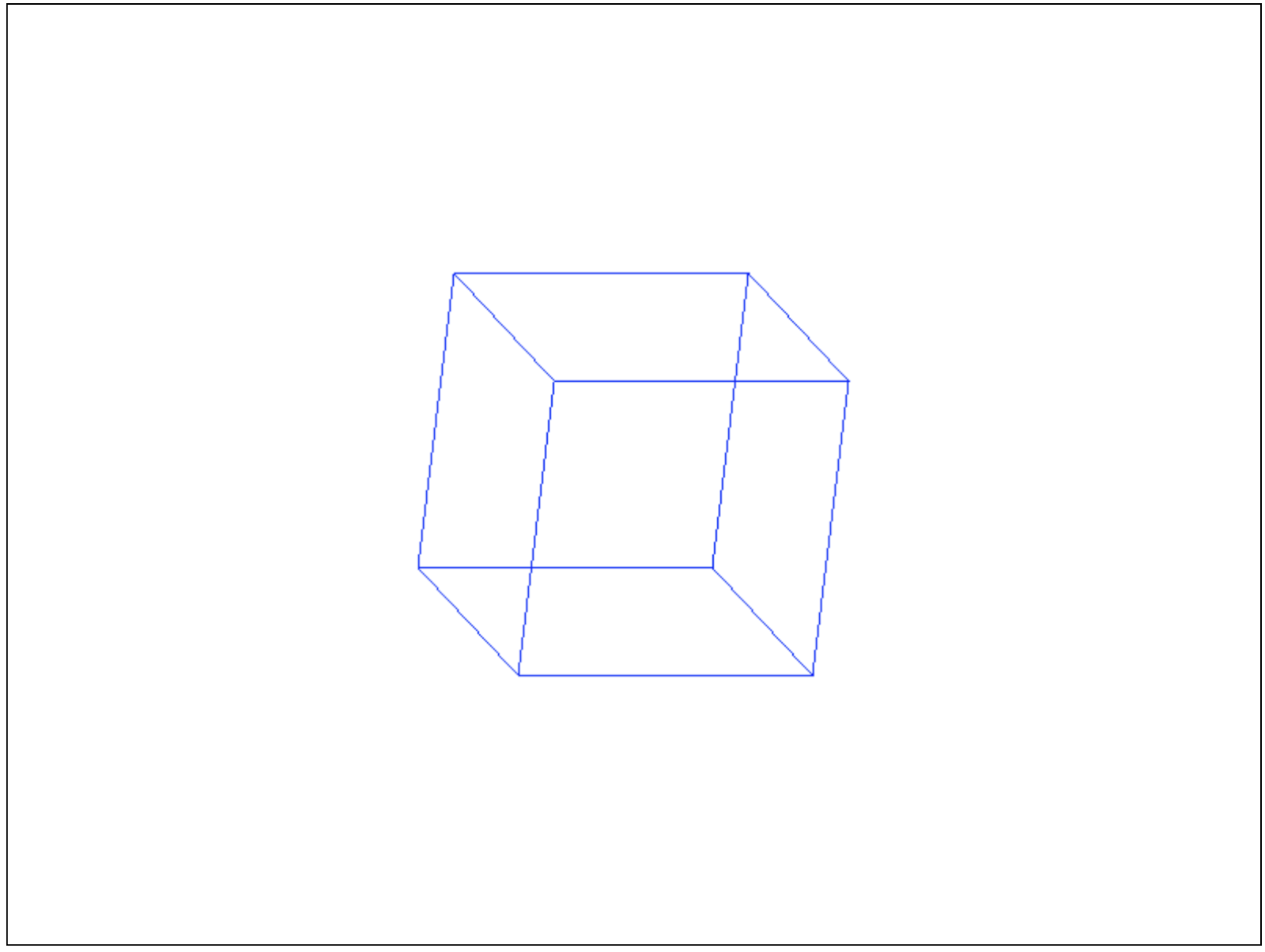
У поворота вокруг осей есть одна особенность, например, если вы повернете куб сначала вокруг оси Y, а потом вокруг оси X, то результаты будут отличаться:

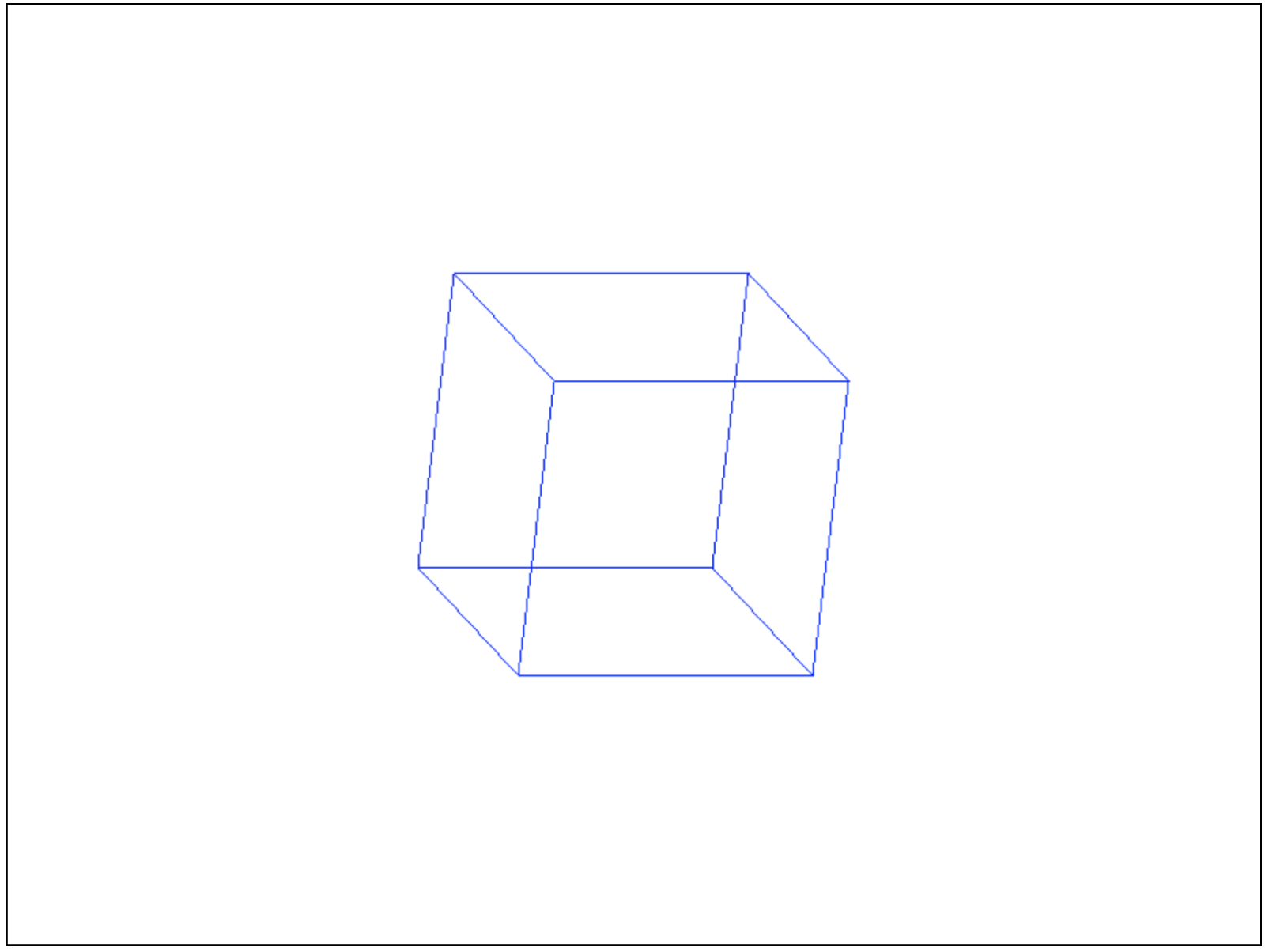
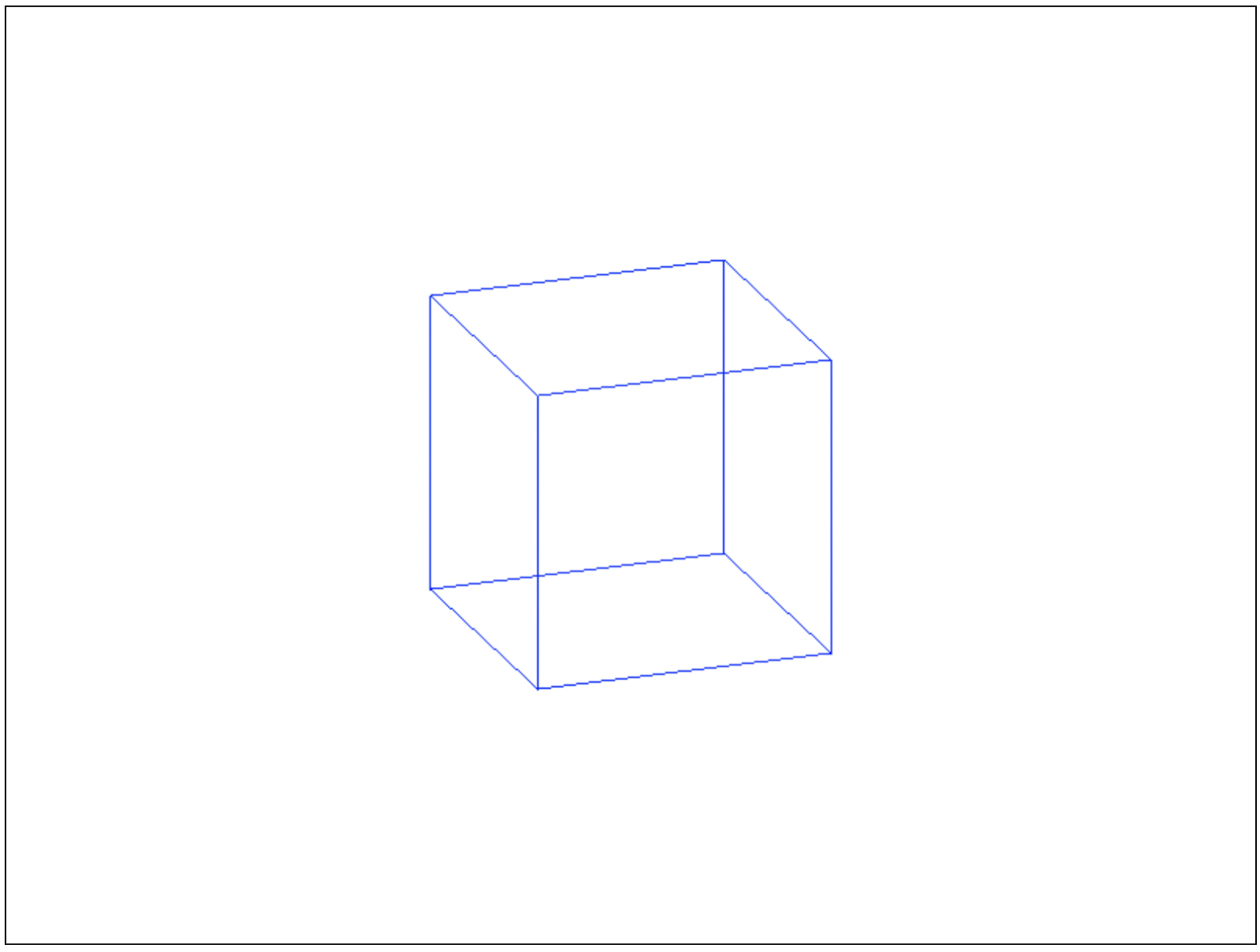
Поворот на 20 градусов вокруг X, затем на 20 градусов вокруг Y	Поворот на 20 градусов вокруг Y, затем на 20 градусов вокруг X

Есть и другие особенности, например, если куб повернуть на 90 градусов по оси Х, затем на 90 градусов по оси Y, и наконец, на 90 градусов вокруг оси Z, то последний поворот вокруг Z, отменит поворот вокруг Х, и получится такой же результат как если бы вы просто повернули фигуру на 90 градусов вокруг оси Y. Чтобы посмотреть почему так происходит, возьмите любой прямоугольный (или кубический) объект в руки (напр. собранный кубик Рубика), запомните начальное положение объекта и проверните его сначала на 90 градусов вокруг воображаемого Х, а затем на 90 градусов вокруг Y и на 90 градусов вокруг Z и запомните, какой стороной он к вам стал, затем начните с запомненного ранее начального положения и проделайте то же самое, убрав повороты повороты X и Z, повернути только вокруг Y — вы увидите, что результат одинаковый. Сейчас мы не будем решать эту проблему и вдаваться в ее подробности, такое вращение на данный момент нас полностью устраивает, но мы эту проблему еще упомянем в третьей части (если хочется подробнее разобраться сейчас, попробуйте поискать статьи на хабре по запросу «шарнирный замок»).

Теперь давайте немного оптимизируем наш код, выше упоминалось, что матричные преобразования можно комбинировать между собой, путем перемножения матриц преобразований. Давайте попробуем не умножать каждый вектор сначала на матрицу поворота вокруг X, затем вокруг Y, затем масштабирования и в конце перемещения, а сначала, до цикла, перемножим все матрицы, а в цикле будем умножать каждую вершину лишь на одну результирующую матрицу, у меня код вышел таким:

let matrix = Matrix.getRotationX(20);

matrix = Matrix.multiply(
  Matrix.getRotationY(20),
  matrix
);

matrix = Matrix.multiply(
  Matrix.getScale(100, 100, 100),
  matrix,
);

matrix = Matrix.multiply(
  Matrix.getTranslation(400, -300, 0),
  matrix,
);

const sceneVertices = [];
for(let i = 0 ; i < vertices.length ; i++) {
  let vertex = Matrix.multiplyVector(
    matrix,
    vertices[i]
  );

  sceneVertices.push(vertex);
}

В данном примере комбинирование преобразований выполняется до цикла 1 раз, и поэтому у нас всего 1 умножение матрицы с каждой вершиной. Если вы запустите этот код, то рисунок куба должен остаться прежним.

Давайте добавим простейшую анимацию, а именно – будем менять угол вращения вокруг оси Y в интервале, например, будем изменять угол вращения вокруг оси  Y на 1 градус, каждые 100 миллисекунд. Для этого нужно положить код конвейера визуализации в функцию setInterval, которую мы впервые использовали в 1-й статье. Код конвейера с анимацией выглядит так:

let angle = 0
setInterval(() => {
  let matrix = Matrix.getRotationX(20)

  matrix = Matrix.multiply(
    Matrix.getRotationY(angle += 1),
    matrix
  )

  matrix = Matrix.multiply(
    Matrix.getScale(100, 100, 100),
    matrix,
  )

  matrix = Matrix.multiply(
    Matrix.getTranslation(400, -300, 0),
    matrix,
  )

  const sceneVertices = []
  for(let i = 0 ; i < vertices.length ; i++) {
    let vertex = Matrix.multiplyVector(
      matrix,
      vertices[i]
    )

    sceneVertices.push(vertex)
  }

  drawer.clearSurface()

  for (let i = 0, l = edges.length ; i < l ; i++) {
    const e = edges[i]

    drawer.drawLine(
      sceneVertices[e[0]].x,
      sceneVertices[e[0]].y,
      sceneVertices[e[1]].x,
      sceneVertices[e[1]].y,
      0, 0, 255
    )
  }

  ctx.putImageData(imageData, 0, 0)
}, 100)

Результат должен быть таким:

Последнее, что мы сделаем в этой части – вывод осей системы координат на экран, чтобы было видно вокруг чего вращается наш куб. Ось Y нарисуем из центра вверх, длинной в 200 пикселей, ось X – вправо, тоже длинной 200 пикселей, а ось Z, нарисуем вниз и влево (по диагонали) длинной 150 пикселей, как это показано в самом начале статьи на рисунке правосторонней системы координат. Начнем с самой простой части, это оси  X, Y, т.к. их линия смещается лишь в одном направлении. После цикла, который рисует куб (цикл перебора edges) добавим отрисовку X, Y осей:

const center = new Vector(400, -300, 0)
drawer.drawLine(
  center.x, center.y,
  center.x, center.y + 200,
  150, 150, 150
)

drawer.drawLine(
  center.x, center.y,
  center.x + 200, center.y,
  150, 150, 150
)

Вектор center это середина окна рисования, т.к. у нас текущие размеры 800 на 600, а -300 для Y я указал, т.к. функция drawPixel переворачивает Y и делает его направление подходящим для canvas (в canvas Y смотрит вниз). Затем мы рисуем 2 оси используя drawLine, смещая сначала Y на 200 пикселей вверх (конец линии оси Y), затем X на 200 пикселей вправо (конец линии оси X). Результат:

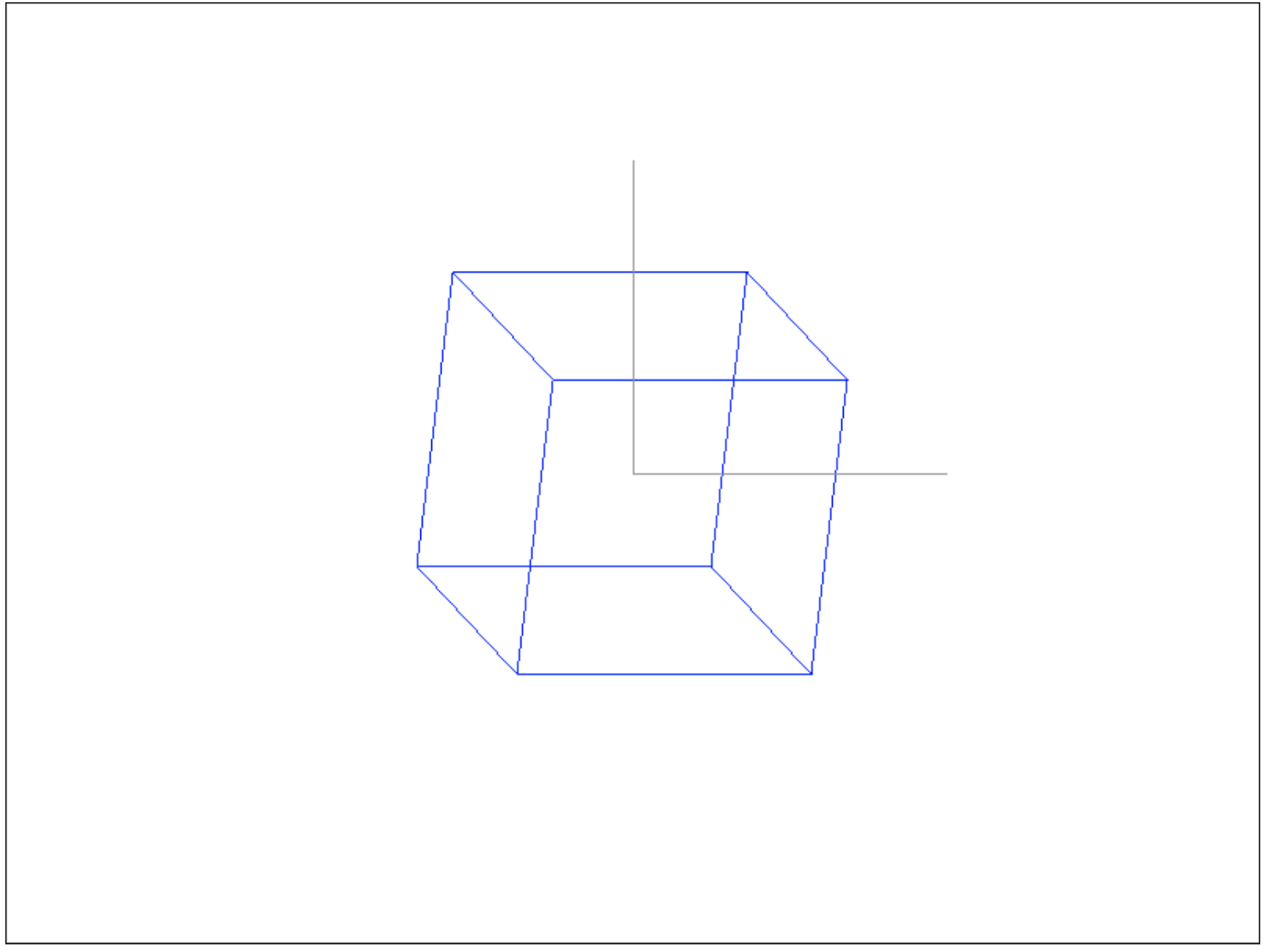
Теперь давайте нарисуем линию оси Z, она диагональная внизвлево и ее вектор смещения будет [-1, -1, 0] и также мы должны нарисовать линию длиной 150 пикселей, т.е. вектор смещения [-1, -1, 0] должен быть длинной 150, первый вариант  это [-150, -150, 0], но если мы посчитаем длину такого вектора, то она будет равняться примерно 212 пикселей. Выше в этой статье мы обсуждали как правильно получить вектор нужной длины. Первым делом нам необходимо его нормализовать, чтобы привести к длине 1, а затем умножить на скаляр той длины, которую хотим получить, в нашем случае это 150. И последним делом просуммируем координаты центра экрана и вектор смещения оси Z, таким образом мы получим, где линия оси Z должна заканчиваться. Давайте напишем код, после кода вывода 2-х предыдущих осей для отрисовки линии оси Z:

const zVector = new Vector(-1, -1, 0);
const zCoords = Vector.add(
  center,
  zVector.normalize().multiplyByScalar(150)
);
drawer.drawLine(
  center.x, center.y,
  zCoords.x, zCoords.y,
  150, 150, 150
);

И в результате вы получите все 3 оси нужной длины:

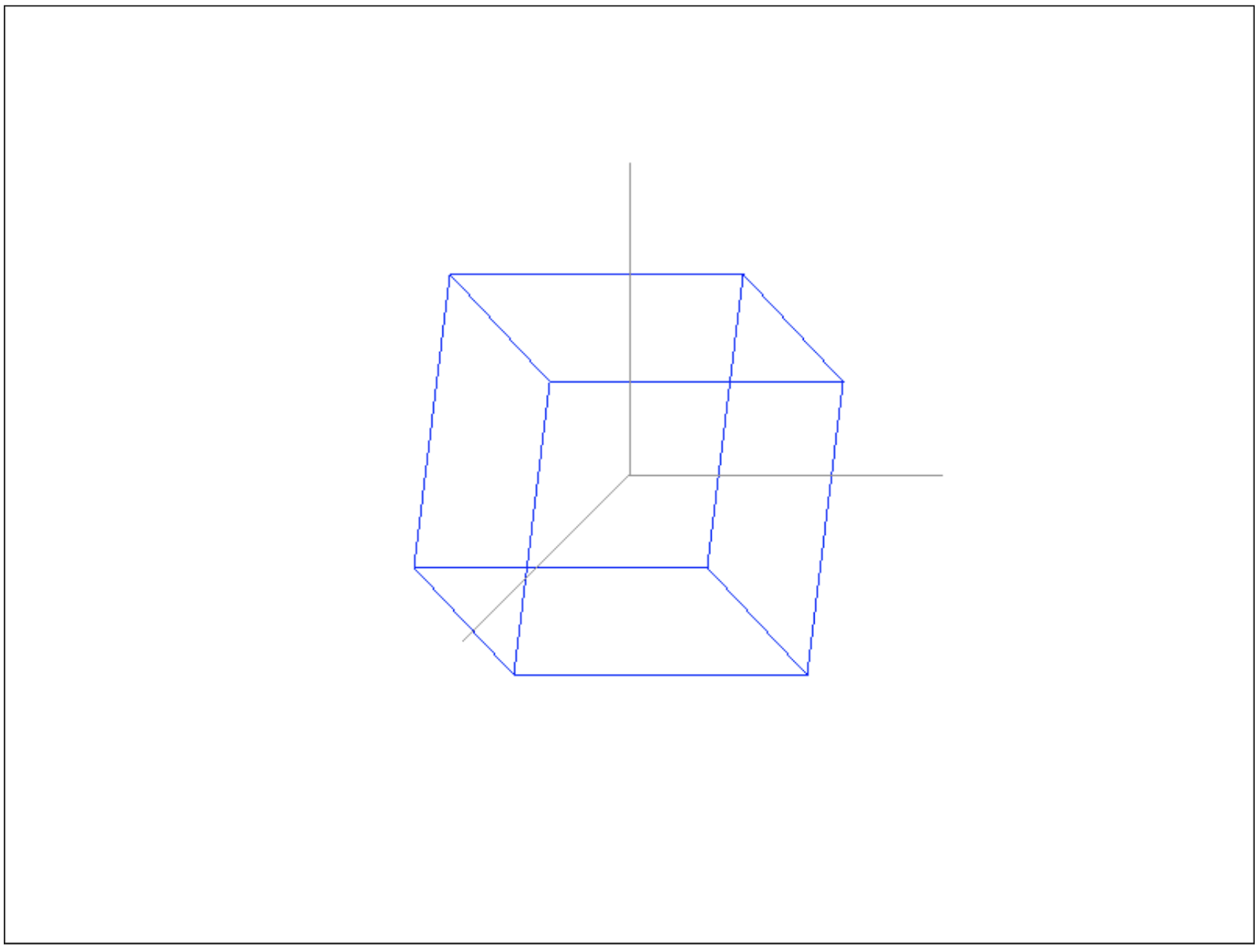
В этом примере ось Z, лишь показывает какая у нас система координат, мы ее нарисовали по диагонали чтобы ее было видно, т.к. настоящая ось Z  перпендикулярна нашем взгляду, и ее мы могли бы нарисовать точкой на экране, что было бы не красиво.

Итого, в это статье мы базово разобрались в системах координат, векторах и с некоторыми операциями над ними, матрицами и их роли в преобразованиях координат, разобрались с вершинами и написали простенький конвейер визуализации куба и осей системы координат, закрепив теорию практикой. Весь код приложения доступен под спойлером:

const ctx = document.getElementById('surface').getContext('2d');
const imageData = ctx.createImageData(800, 600);

class Vector {
  x = 0;
  y = 0;
  z = 0;
  w = 1;

  constructor(x, y, z, w = 1) {
    this.x = x;
    this.y = y;
    this.z = z;
    this.w = w;
  }

  multiplyByScalar(s) {
    this.x *= s;
    this.y *= s;
    this.z *= s;

    return this;
  }

  static add(v1, v2) {
    return new Vector(
      v1.x + v2.x,
      v1.y + v2.y,
      v1.z + v2.z,
    );
  }

  getLength() {
    return Math.sqrt(
      this.x * this.x + this.y * this.y + this.z * this.z
    );
  }

  normalize() {
    const length = this.getLength();

    this.x /= length;
    this.y /= length;
    this.z /= length;

    return this;
  }
}

class Matrix {
  static multiply(a, b) {
    const m = [
      [0, 0, 0, 0],
      [0, 0, 0, 0],
      [0, 0, 0, 0],
      [0, 0, 0, 0],
    ];

    for (let i = 0 ; i < 4 ; i++) {
      for(let j = 0 ; j < 4 ; j++) {
        m[i][j] = a[i][0] * b[0][j] +
          a[i][1] * b[1][j] +
          a[i][2] * b[2][j] +
          a[i][3] * b[3][j];
      }
    }

    return m;
  }

  static getRotationX(angle) {
    const rad = Math.PI / 180 * angle;

    return [
      [1, 0, 0, 0],
      [0, Math.cos(rad), -Math.sin(rad), 0],
      [0, Math.sin(rad), Math.cos(rad), 0],
      [0, 0, 0, 1],
    ];
  }

  static getRotationY(angle) {
    const rad = Math.PI / 180 * angle;

    return [
      [Math.cos(rad), 0, Math.sin(rad), 0],
      [0, 1, 0, 0],
      [-Math.sin(rad), 0, Math.cos(rad), 0],
      [0, 0, 0, 1],
    ];
  }

  static getRotationZ(angle) {
    const rad = Math.PI / 180 * angle;

    return [
      [Math.cos(rad), -Math.sin(rad), 0, 0],
      [Math.sin(rad), Math.cos(rad), 0, 0],
      [0, 0, 1, 0],
      [0, 0, 0, 1],
    ];
  }

  static getTranslation(dx, dy, dz) {
    return [
      [1, 0, 0, dx],
      [0, 1, 0, dy],
      [0, 0, 1, dz],
      [0, 0, 0, 1],
    ];
  }

  static getScale(sx, sy, sz) {
    return [
      [sx, 0, 0, 0],
      [0, sy, 0, 0],
      [0, 0, sz, 0],
      [0, 0, 0, 1],
    ];
  }

  static multiplyVector(m, v) {
    return new Vector(
      m[0][0] * v.x + m[0][1] * v.y + m[0][2] * v.z + m[0][3] * v.w,
      m[1][0] * v.x + m[1][1] * v.y + m[1][2] * v.z + m[1][3] * v.w,
      m[2][0] * v.x + m[2][1] * v.y + m[2][2] * v.z + m[2][3] * v.w,
      m[3][0] * v.x + m[3][1] * v.y + m[3][2] * v.z + m[3][3] * v.w,
    );
  }
}

class Drawer {
  surface = null;
  width = 0;
  height = 0;

  constructor(surface, width, height) {
    this.surface = surface;
    this.width = width;
    this.height = height;
  }

  drawPixel(x, y, r, g, b) {
    const offset = (this.width * -y + x) * 4;

    if (x >= 0 && x < this.width && -y >= 0 && -y < this.height) {
      this.surface[offset] = r;
      this.surface[offset + 1] = g;
      this.surface[offset + 2] = b;
      this.surface[offset + 3] = 255;
    }
  }
  drawLine(x1, y1, x2, y2, r = 0, g = 0, b = 0) {
    const round = Math.trunc;
    x1 = round(x1);
    y1 = round(y1);
    x2 = round(x2);
    y2 = round(y2);

    const c1 = y2 - y1;
    const c2 = x2 - x1;

    const length = Math.max(
      Math.abs(c1),
      Math.abs(c2)
    );

    const xStep = c2 / length;
    const yStep = c1 / length;

    for (let i = 0 ; i <= length ; i++) {
      this.drawPixel(
        Math.trunc(x1 + xStep * i),
        Math.trunc(y1 + yStep * i),
        r, g, b,
      );
    }
  }

  clearSurface() {
    const surfaceSize = this.width * this.height * 4;
    for (let i = 0; i < surfaceSize; i++) {
      this.surface[i] = 0;
    }
  }
}

const drawer = new Drawer(
  imageData.data,
  imageData.width,
  imageData.height
);

// Cube vertices
const vertices = [
  new Vector(-1, 1, 1), // 0 вершина
  new Vector(-1, 1, -1), // 1 вершина
  new Vector(1, 1, -1), // 2 вершина
  new Vector(1, 1, 1), // 3 вершина
  new Vector(-1, -1, 1), // 4 вершина
  new Vector(-1, -1, -1), // 5 вершина
  new Vector(1, -1, -1), // 6 вершина
  new Vector(1, -1, 1), // 7 вершина
];

// Cube edges
const edges = [
  [0, 1],
  [1, 2],
  [2, 3],
  [3, 0],

  [0, 4],
  [1, 5],
  [2, 6],
  [3, 7],

  [4, 5],
  [5, 6],
  [6, 7],
  [7, 4],
];

let angle = 0;
setInterval(() => {
  let matrix = Matrix.getRotationX(20);

  matrix = Matrix.multiply(
    Matrix.getRotationY(angle += 1),
    matrix
  );

  matrix = Matrix.multiply(
    Matrix.getScale(100, 100, 100),
    matrix,
  );

  matrix = Matrix.multiply(
    Matrix.getTranslation(400, -300, 0),
    matrix,
  );

  const sceneVertices = [];
  for(let i = 0 ; i < vertices.length ; i++) {
    let vertex = Matrix.multiplyVector(
      matrix,
      vertices[i]
    );

    sceneVertices.push(vertex);
  }

  drawer.clearSurface();

  for (let i = 0, l = edges.length ; i < l ; i++) {
    const e = edges[i];

    drawer.drawLine(
      sceneVertices[e[0]].x,
      sceneVertices[e[0]].y,
      sceneVertices[e[1]].x,
      sceneVertices[e[1]].y,
      0, 0, 255
    );
  }

  const center = new Vector(400, -300, 0)
  drawer.drawLine(
    center.x, center.y,
    center.x, center.y + 200,
    150, 150, 150
  );

  drawer.drawLine(
    center.x, center.y,
    center.x + 200, center.y,
    150, 150, 150
  );

  const zVector = new Vector(-1, -1, 0, 0);
  const zCoords = Vector.add(
    center,
    zVector.normalize().multiplyByScalar(150)
  );
  drawer.drawLine(
    center.x, center.y,
    zCoords.x, zCoords.y,
    150, 150, 150
  );

  ctx.putImageData(imageData, 0, 0);
}, 100);

Что дальше?

В следующей части рассмотрим, как управлять камерой и как делать проекцию (чем дальше объект, тем он меньше), познакомимся с треугольниками и узнаем, как из них можно построить 3D-модели, разберем, что такое нормали и зачем они нужны.

Автор: Александр

Источник