Одним вечером я наткнулся на статью о реализации одномерного клеточного автомата с помощью комонад, однако материал неполон и немного устарел, в связи с чем решил написать русскоязычную адаптацию (заодно рассмотрев двумерные клеточные автоматы на примере Game of Life)
Метка «game of life»
Клеточные автоматы с помощью комонад
2014-06-06 в 12:21, admin, рубрики: game of life, haskell, жизнь, клеточный автомат, функциональное программирование, метки: game of life, haskell, жизнь, клеточный автомат
Игра Жизнь на LiveScript в 30 строк
2013-11-19 в 13:01, admin, рубрики: 30 строк, 30строк, game of life, javascript, life, livescript, Веб-разработка, жизнь, игра, игра жизнь, матрица, ненормальное программирование, симуляция, строк, метки: 30 строк, 30строк, game of life, javascript, life, livescript, жизнь, игра, игра жизнь, матрица, симуляция, строк В продолжение 30-ти строчного мема, выкладываю реализацию известной игры Жизнь на LiveScript (язык, транслируемый в Javascript).
Читать полностью »
Жизнь на плоскости Лобачевского
2013-02-05 в 20:25, admin, рубрики: game development, game of life, Алгоритмы, игра жизнь, математика, метки: game of life, игра жизнь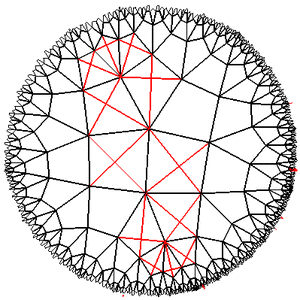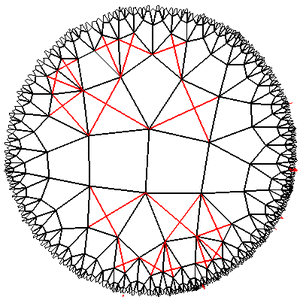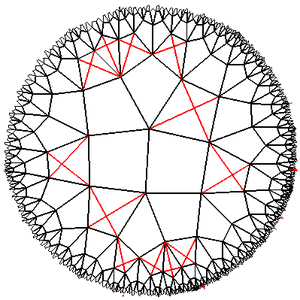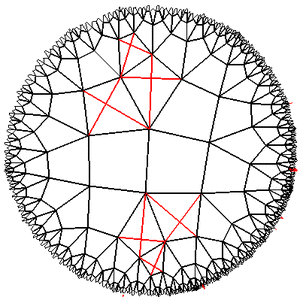 
Различные реализации игры «Жизнь» описывались на Хабре уже неоднократно. В этой статье, в качестве продолжения этой темы, рассматривается ещё один её вариант: в качестве игрового поля используется регулярная решётка на плоскости Лобаческого. Описываются общие методы использования плоскости Лобачевского в программах и необходимые для этого математические приёмы.
Как возникла плоскость Лобачевского, достаточно известно. В позапрошлом веке господа Гаусс, Лобачевский и Бойяи, проживавшие примерно в одно время в разных странах тогдашней Европы, задумались, что будет, если отменить пятый постулат Евклида и заменить его на противоположную аксиому. Оказалось, что не случится ничего плохого, и никаких противоречий не возникнет. Заметная часть последующего изучения неевклидовой геометрии была посвящена выяснению того, кто из них у кого украл идею этой самой геометрии.
Менее известно, что несмотря на «отрицательный» способ определения неевклидовой геометрии (вместо того, чтобы сказать, что через точку проходит ровно одна прямая, не пересекающая данную, мы говорим, что таких прямых может быть сколько угодно), мы, тем не менее, получаем систему теорем и формул, не менее стройную, чем та, что есть в евклидовой геометрии. И одновременно, у нас есть гораздо большее разнообразие геометрических фигур, в том числе, разбиений плоскости на правильные многоугольники.