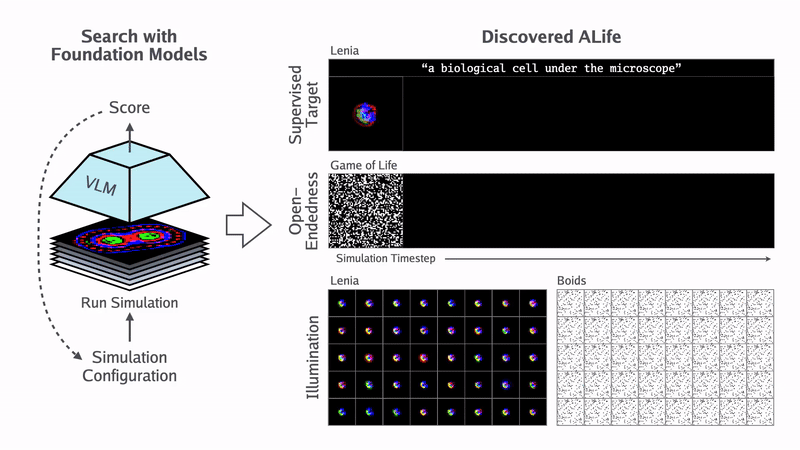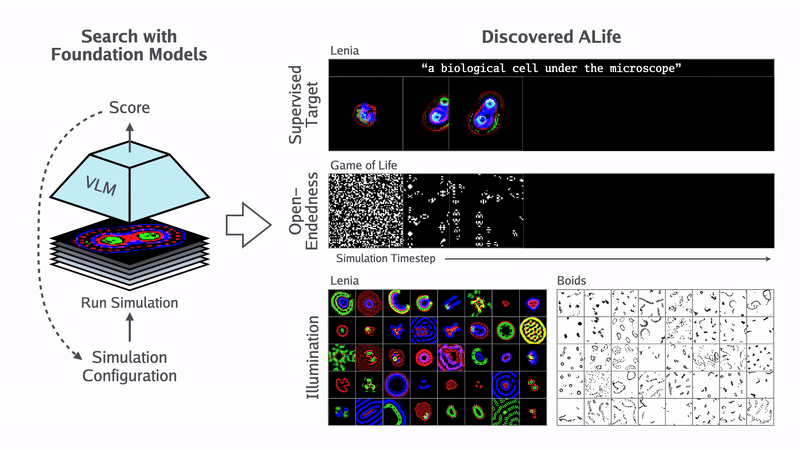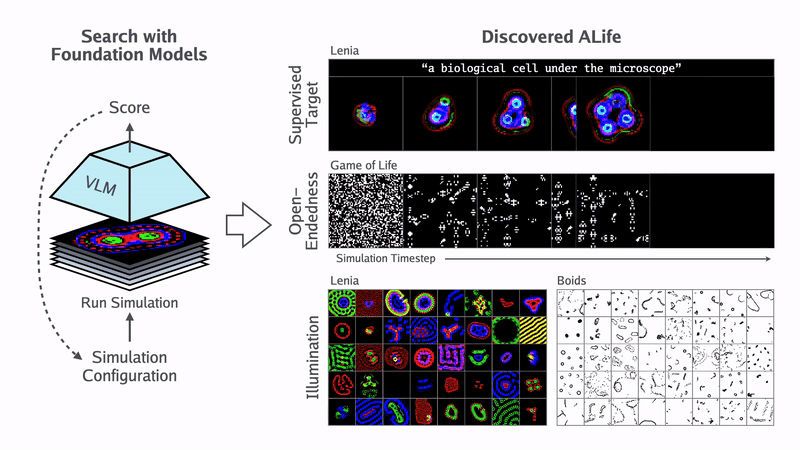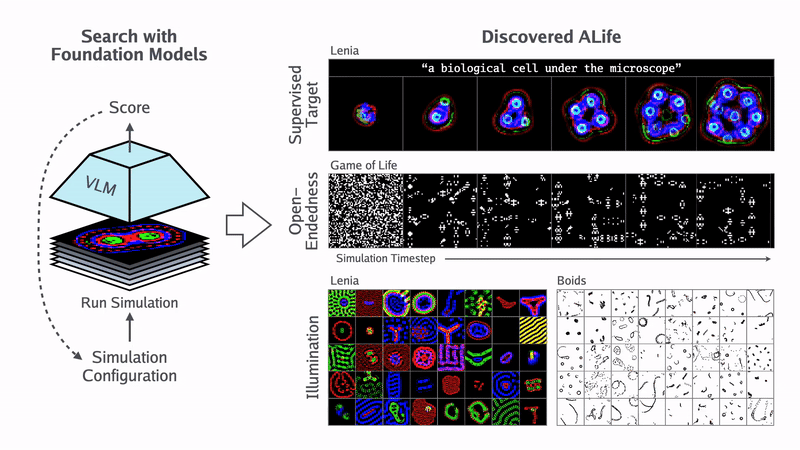
Некоторые люди смотрят «Матрицу» и думают, что это выдумка. Конечно, там есть приукрашивания и преувеличения о ценности человеческих тел, но в целом гипотеза симуляции построена на стройной научной модели цифровой физики.
Цифровая физика — это совокупность математических и философских работ, представляющих Вселенную как гигантский цифровой компьютер.
В этом направлении работали великие учёные и инженеры, такие как Конрад Цузе (создатель Читать полностью »
WebAssembly являясь (относительно) молодой технологией уже довольно распространён в индустрииЧитать полностью »
В 40-е годы XX века работа Фон Неймана в области самовоспроизводящихся машин привела к появлению теории клеточных автоматов. Оттуда же берёт своё начало не безызвестная "Game of Life" - математическая модель примитивной жизни захватывающая умы простотой своего описании и сложностью порождаемых ею систем.
Поиск искусственной жизни (artificial life или A-life) — это область науки, исследующая модели живых систем и их эволюцию в контролируемых условиях, чаще всего — в компьютерных симуляциях. поиски эти раньше часто проводились вручную, а рисерчеры из ИИ-лаборатории Sakana AI предложили новый подход к автоматизации поиска с использованием ИИ моделей, таких как CLIP.
Тридцать восемь лет назад в свои тридцать восемь лет аспирант Мичиганского университета Крис Лэнгтон придумал два простых правила для клеточного автомата. Мы быстро повторим правила Лэнгтона, оживим муравья, написав код онлайн, добавим динамики (плавная анимация) и интерактивности (редактор уровней). Повоюем, постреляем купидоновыми стрелами, порисуем на заборе. А ещё педагогически немного адаптируем код для занятий с детьми (опционально).
Продолжим экспериментировать с клеточными автоматами прямо в браузере (или в VS CodeЧитать полностью »
Привет! Сегодня мы поговорим о том, как сделать код не просто красивым, но и живым. Звучит как научная фантастика, либо вы уже подготовились к очередной банальности про искусственный интеллект, но не в этом посте. В 1970 году британский математик Джон Хортон Конвей показал миру, что даже простейшие алгоритмы могут порождать сложные, живые системы, которые ещё и к тому же полные по Тьюрингу. И что код может быть не только красивым, но и живым.
👾!
Возвращаемся к нашей экскурсии по модификациям клеточных автоматов. Объект сегодняшнего внимания – дефицитные правила (deficient rules). Это ещё более свежая вариация, чем рассмотренный в прошлом посте , и была описана 5 лет назад энтузиастом 83bismuth38.
Модификация предполагает, что при рождении клетки на окружающих соседей налагается ограничение на рождение по этому переходу, согласно нотации Хенселя. Освежить в памяти, что из себя представляют переходы можно здесь.Читать полностью »
👾!
В прошлой статье о циклических КА мы мельком затронули тему альтернативных окрестностей, рассмотрев несколько примеров. Несмотря на то, что ранее мы использовали только окрестности Мура и фон Неймана, существует ещё множество прочих именованных окрестностей, а потенциал для создания новых ограничен лишь нашей фантазией.
Сегодняшний обзор мы совместим с ещё одним расширением: в статье об LtL было упомянуто, что параметры рождения и выживания клетки могут поддерживать множество значений и диапазонов в некоторых прочих конфигурациях. В первую очередь речь шла о HROT (Higher-Range Outer-Totalistic) – обобщении LtL конфигурации, на котором и будут наши сегодняшние примеры.
Читать полностью »
В одной из своих прошлых статей по эволюции случайной конфигурации в игре жизнь я выдвинул гипотезу: Первая гипотеза касается окончания 'движухи' - в широком диапазоне изначальных плотностей p от 0.1 до 0.7, после окончания 'движухи' 'пепел' имеет одну и ту же плотность, около 0.27
