К рассмотрению предлагается одна из возможных реализаций алгоритма минимизации логических (булевых) функций (ЛФ) заданных в виде совершенной дизъюнктивной нормальной формы (СДНФ) методом КвайнаМак-Класки (далее просто Мак-Класки) и проблемы, выявленные при её тестировании. В исследуемом варианте алгоритм Мак-Класки реализован на языке C# с использованием Generic-коллекций библиотеки .NET.
Хотелось бы отметить, что задача минимизации ЛФ, по моему мнению, незаслуженно обходится стороной в тематике алгоритмов машинного обучения, т. к. по своему смыслу она реализует процедуру обучения с учителем для определённого набора входных терм (простых конъюнкций), на которых оптимизируемая функция принимает истинное (true) значение. Следовательно, этот набор входных терм, из общего их возможного числа $inline$2^N$inline$, где N – количество двух классовых категориальных (двоичных) переменных в термах, является обучающей выборкой для задачи обучения с учителем с известным (данном случае истинным) выходным значением целевой функции. Для всех остальных возможных терм, не входящих в обучающую выборку, минимизированная ЛФ должна принимать ложное (false) значение.
Одним из легко реализуемых для любого количества входных переменных алгоритмов минимизации ЛФ является метод Мак-Класки. Согласно теории метод Мак-Класки состоит из двух основных этапов:
- Нахождение всех простых терм ЛФ, используя правило (законы) склеивания:
a) (A & B) ∨ (A & !B) ≡ A;
b) (A ∨ B) & (A ∨ !B) ≡ A;
где & — операция логического «И»; ∨ — операция логического «ИЛИ»;! – операция логического отрицания «НЕ». - Минимизация количества простых терм полученного множества, как задача нахождения оптимального покрытия множества подмножествами разной длины.
using System;
using System.IO;
using System.Collections.Generic;
using System.Linq;
/// <summary>
/// Базовый класс для логических функций
/// </summary>
public abstract class LogicFunction
{
//Дизъюнкции или конъюнкции функции
public readonly ICollection<char[]> Terms = new LinkedList<char[]>();
//Вычисление значения функции
public abstract bool Calculate(bool[] X);
//Вычисление значения функции
public virtual bool Calculate(char[] X)
{
return Calculate(X.Select(p => p != '0').ToArray());
}
}
/// <summary>
/// Дизъюнктивная нормальная форма
/// </summary>
public class Dnf : LogicFunction
{
public override bool Calculate(bool[] X)
{
bool bResult = false;
foreach (char[] term in Terms)
{
bool TermVal = true;
for (int i = 0; i < term.Length; i++)
{
if (term[i] == '*') continue;
TermVal &= (term[i] != '0' ? X[i] : !X[i]);
}
bResult |= TermVal;
}
return bResult;
}
}
/// <summary>
/// Конъюнктивная нормальная форма
/// </summary>
public class Knf : LogicFunction
{
public override bool Calculate(bool[] X)
{
bool bResult = true;
foreach (char[] term in Terms)
{
bool TermVal = false;
for (int i = 0; i < term.Length; i++)
{
if (term[i] == '*') continue;
TermVal |= (term[i] != '0' ? X[i] : !X[i]);
}
bResult &= TermVal;
}
return bResult;
}
}
/// <summary>
/// Минимизация логической функции методом Квайна---Мак-Класки
/// </summary>
public class Quine_McCluskey
{
private readonly Dnf _result = new Dnf();
public Dnf Result
{
get { return _result; }
}
//Запуск метода
public void Start(IEnumerable<char[]> TermInput)
{
LogicFuncMinimize(TermInput, _result.Terms);
}
//Запуск метода
public void Start(string sFileName)
{
Start(LoadDsnfFromFile(sFileName));
}
//Нахождение минимальной логической функции
private static void LogicFuncMinimize(IEnumerable<char[]> X1, ICollection<char[]> OutR)
{
Dictionary<int, LinkedList<TreeNodeEnd>> OutTemp = new Dictionary<int, LinkedList<TreeNodeEnd>>();
if (X1.First().Length <= 40)
{
Dictionary<UInt64, TreeNodeEnd> X1Tree = new Dictionary<UInt64, TreeNodeEnd>();
DeleteDublicatingTerms(X1, X1Tree);
int iLevelCounter = 0;
//Повтор до тех пор пока будут оставаться термы
while (X1Tree.Count != 0)
{
Dictionary<UInt64, TreeNodeEnd> X2Tree = new Dictionary<UInt64, TreeNodeEnd>();
Skleivanie(X1Tree, X2Tree, OutTemp, iLevelCounter++);
X1Tree = X2Tree;
GC.Collect(); //Отсутствие сборки мусора очень сильно влияет на время работы!!!
}
}
else
{
TreeFuncTerm X1Tree = new TreeFuncTerm();
DeleteDublicatingTerms(X1, X1Tree);
int iLevelCounter = 0;
//Повтор до тех пор пока будут оставаться термы
while (X1Tree.Count != 0)
{
TreeFuncTerm X2Tree = new TreeFuncTerm();
Skleivanie(X1Tree, X2Tree, OutTemp, iLevelCounter++);
X1Tree = X2Tree;
GC.Collect(); //Отсутствие сборки мусора очень сильно влияет на время работы!!!
}
}
HashSet<TreeNodeEnd> OutRes = new HashSet<TreeNodeEnd>();
ReduceRedundancyTerms(OutTemp, OutRes);
OutR.Clear();
foreach (TreeNodeEnd term in OutRes) OutR.Add(term.Term);
}
//Процедура чтения ДСНФ из файла и запись в матрицу
private static ICollection<char[]> LoadDsnfFromFile(string sFullFileName)
{
ICollection<char[]> DSNF = new LinkedList<char[]>();
//Чтение строк из файла
using (StreamReader InFile = new StreamReader(sFullFileName))
{
string sLine = "";
while ((sLine = InFile.ReadLine()) != null)
{
DSNF.Add(sLine.ToArray());
}
}
return DSNF;
}
//Удаление дубликатов термов из входного списка
//В выходной словарь добавляются только уникальные термы
private static void DeleteDublicatingTerms(IEnumerable<char[]> InX1,
Dictionary<UInt64, TreeNodeEnd> OutX2Tree)
{
OutX2Tree.Clear();
TreeNodeEnd pCurrNode = null;
foreach (char[] x1 in InX1)
{
UInt64 iCode = GetTermCode(x1);
if (OutX2Tree.ContainsKey(iCode)) continue;
pCurrNode = new TreeNodeEnd(x1, null, null, pCurrNode, OutX2Tree.Count);
OutX2Tree.Add(iCode, pCurrNode);
}
}
//Удаление дубликатов термов из входного списка
//В выходное дерево добавляются только уникальные термы
private static void DeleteDublicatingTerms(IEnumerable<char[]> InX1, TreeFuncTerm OutX2Tree)
{
OutX2Tree.Clear();
foreach (char[] x1 in InX1)
{
OutX2Tree.AddTerm(x1, null, null);
}
}
//Склеивание строк с одним различием
private static void Skleivanie(TreeFuncTerm X1Tree, TreeFuncTerm X2Tree,
Dictionary<int, LinkedList<TreeNodeEnd>> OutResult, int iLevel)
{
LinkedList<TreeNodeEnd> OutR = new LinkedList<TreeNodeEnd>();
OutResult.Add(iLevel, OutR);
Dictionary<int, TreeNodeEnd> FindTerms = new Dictionary<int, TreeNodeEnd>();
TreeNodeEnd x1 = X1Tree.Last;
while (x1 != null)
{
X1Tree.SearchDiff1(x1, FindTerms);
if (FindTerms.Count == 0)
{
//Добавление на выход тех термов, которые ни с кем не склеились
OutR.AddLast(x1);
}
else
{
foreach (KeyValuePair<int, TreeNodeEnd> kvp in FindTerms)
{
//Проверка, чтобы комбинации термов обрабатывались только по одному разу
if (x1.Number < kvp.Value.Number) continue;
//Склеивание двух термов с одним различием
char cSymbSav = x1.Term[kvp.Key];
x1.Term[kvp.Key] = '*'; //Метка склеивания
X2Tree.AddTerm(x1.Term, x1, kvp.Value);
x1.Term[kvp.Key] = cSymbSav;
}
}
x1 = x1.Prev;
}
}
//Возвращает уникальный код для терма
private static UInt64 GetTermCode(char[] pTerm)
{
UInt64 iMultip = 1, iCode = 0;
for (int i = 0; i < pTerm.Length; i++)
{
switch (pTerm[i])
{
case '0':
break;
case '1':
iCode += iMultip;
break;
case '*':
iCode += (iMultip + iMultip);
break;
}
iMultip *= 3;
}
return iCode;
}
//Склеивание строк с одним различием
private static void Skleivanie(Dictionary<UInt64, TreeNodeEnd> X1Tree, Dictionary<UInt64,
TreeNodeEnd> X2Tree, Dictionary<int, LinkedList<TreeNodeEnd>> OutResult, int iLevel)
{
LinkedList<TreeNodeEnd> OutR = new LinkedList<TreeNodeEnd>();
OutResult.Add(iLevel, OutR);
foreach (KeyValuePair<UInt64, TreeNodeEnd> x1 in X1Tree)
{
bool bIsSkleiv = false;
UInt64 iMultip = 1;
for (int iPos = 0; iPos < x1.Value.Term.Length; iPos++)
{
char cSymbSav = x1.Value.Term[iPos];
if (cSymbSav != '*')
{
UInt64 iCode;
if (cSymbSav == '0')
iCode = x1.Key + iMultip;
else //_if (cSymbSav == '1')
iCode = x1.Key - iMultip;
TreeNodeEnd pSkleivNode = null;
X1Tree.TryGetValue(iCode, out pSkleivNode);
if (pSkleivNode != null)
{
bIsSkleiv = true;
//Проверка, чтобы комбинации термов обрабатывались только по одному разу
if (x1.Value.Number > pSkleivNode.Number)
{
//Склеивание двух термов с одним различием
if (cSymbSav == '0')
iCode = x1.Key + iMultip + iMultip;
else //_if (cSymbSav == '1')
iCode = x1.Key + iMultip;
x1.Value.Term[iPos] = '*'; //Метка склеивания
if (!X2Tree.ContainsKey(iCode)) X2Tree.Add(iCode,
new TreeNodeEnd(x1.Value.Term, x1.Value, pSkleivNode, null, X2Tree.Count));
x1.Value.Term[iPos] = cSymbSav;
}
}
}
iMultip *= 3;
}
if (!bIsSkleiv)
{
//Добавление на выход тех термов, которые ни с кем не склеились
OutR.AddLast(x1.Value);
}
}
}
// Отбрасывание избыточных терм с помощью алгоритма приближенного решения задачи о покрытии.
private static void ReduceRedundancyTerms(Dictionary<int, LinkedList<TreeNodeEnd>> X,
HashSet<TreeNodeEnd> ResultNumbers)
{
//Подготовка результирующего контейнера
ResultNumbers.Clear();
//Контейнер первичных входных термов с распределением по кол-ву образовавших выходные термы
HashSet<TreeNodeEnd> pNumbersForAdd = new HashSet<TreeNodeEnd>();
Dictionary<TreeNodeEnd, uint> Numbers2Terms = new Dictionary<TreeNodeEnd, uint>();
Dictionary<TreeNodeEnd, HashSet<TreeNodeEnd>> Terms2Numbers =
new Dictionary<TreeNodeEnd, HashSet<TreeNodeEnd>>();
//Формирование распределения по уровню
foreach (int iLevel in X.Keys.OrderByDescending(p => p).AsQueryable())
{
foreach (TreeNodeEnd term in X[iLevel])
{
HashSet<TreeNodeEnd> TermNumberCont = new HashSet<TreeNodeEnd>();
HashSet<TreeNodeEnd> ListNumbers = new HashSet<TreeNodeEnd>();
ListNumbers.Add(term);
while (ListNumbers.Count > 0)
{
TreeNodeEnd pCurrNode = ListNumbers.First();
ListNumbers.Remove(pCurrNode);
if (pCurrNode.Parent1 != null && pCurrNode.Parent2 != null)
{
ListNumbers.Add(pCurrNode.Parent1);
ListNumbers.Add(pCurrNode.Parent2);
}
else
{
if (!Numbers2Terms.ContainsKey(pCurrNode)) Numbers2Terms.Add(pCurrNode, 0);
Numbers2Terms[pCurrNode]++;
//Добавление номера в контейнер
TermNumberCont.Add(pCurrNode);
}
}
//int iIntersectNumbers = pNumbersForAdd.Intersect(TermNumberCont).Count();
//if (iIntersectNumbers < TermNumberCont.Count)
{
pNumbersForAdd.UnionWith(TermNumberCont);
Terms2Numbers.Add(term, TermNumberCont);
}
}
}
//Выполняется первый принцип - первыми обрабатываются минимальные столбцы ТП
pNumbersForAdd = new HashSet<TreeNodeEnd>(pNumbersForAdd.OrderBy(p => Numbers2Terms[p]));
//Контейнер для хранения отобранных выходных термов с их связями с входными
Dictionary<TreeNodeEnd, HashSet<TreeNodeEnd>> SelectedTerms =
new Dictionary<TreeNodeEnd, HashSet<TreeNodeEnd>>();
//Перебор всех первичных входных термов
while (pNumbersForAdd.Count > 0)
{
//Проверяемый входной терм
TreeNodeEnd pSrcTerm = pNumbersForAdd.First();
//Отбор лучшего выходного терма, который был образован с участием данного входного терма
TreeNodeEnd BestTerm = null;
int iBestTermNumbersCount = 0;
foreach (KeyValuePair<TreeNodeEnd, HashSet<TreeNodeEnd>> CurrTerm in Terms2Numbers)
{
if (!CurrTerm.Value.Contains(pSrcTerm)) continue;
int iCurrTermNumbersCount = CurrTerm.Value.Intersect(pNumbersForAdd).Count();
if ((BestTerm == null) || (iBestTermNumbersCount < iCurrTermNumbersCount))
{
BestTerm = CurrTerm.Key;
iBestTermNumbersCount = iCurrTermNumbersCount;
}
}
ResultNumbers.Add(BestTerm);
HashSet<TreeNodeEnd> pBestTermSrcNodes = Terms2Numbers[BestTerm];
Terms2Numbers.Remove(BestTerm);
SelectedTerms.Add(BestTerm, pBestTermSrcNodes);
pNumbersForAdd.RemoveWhere(p => pBestTermSrcNodes.Contains(p));
}
//Чтобы освободить неиспользуемую память
Terms2Numbers = SelectedTerms;
//Теперь проверка на возможность выкинуть из списка отобранных
TreeNodeEnd termForDelete = null;
do
{
termForDelete = null;
int iTermForDeleteUsedNumbCount = 0;
foreach (KeyValuePair<TreeNodeEnd, HashSet<TreeNodeEnd>> term1 in SelectedTerms)
{
int iUsedNumbCounter = 0;
foreach (TreeNodeEnd numb in term1.Value)
{
bool bFind = false;
foreach (KeyValuePair<TreeNodeEnd, HashSet<TreeNodeEnd>> term2 in SelectedTerms)
{
if (term1.Key == term2.Key) continue;
if (bFind = term2.Value.Contains(numb)) break;
}
if (bFind) iUsedNumbCounter++;
}
if ((iUsedNumbCounter == term1.Value.Count) && ((termForDelete == null) ||
(iUsedNumbCounter <= iTermForDeleteUsedNumbCount)))
{
termForDelete = term1.Key;
iTermForDeleteUsedNumbCount = iUsedNumbCounter;
}
}
if (termForDelete != null)
{
ResultNumbers.Remove(termForDelete);
SelectedTerms.Remove(termForDelete);
}
} while (termForDelete != null);
}
}
/// <summary>
/// Дерево термов
/// </summary>
public class TreeFuncTerm
{
//Корень
private readonly TreeNodeMiddle rootNode = new TreeNodeMiddle();
//Ссылка на завершающий узел последовательности ссылок на конечные листья дерева
private TreeNodeEnd _lastTreeNode = null;
public TreeNodeEnd Last
{
get { return _lastTreeNode; }
}
//Возвращает количество термов в дереве
private int _count = 0;
public int Count
{
get { return _count; }
}
//Конструктор
public TreeFuncTerm()
{
Clear();
}
//Очистить дерево
public void Clear()
{
rootNode.Clear();
_count = 0;
_lastTreeNode = null;
}
//Добавление в дерево нового терма
public void AddTerm(char[] term, TreeNodeEnd pParent1, TreeNodeEnd pParent2)
{
TreeNodeMiddle pCurrNode = rootNode;
for (int j = 0; j < term.Length; j++)
{
TreeNodeBase item = pCurrNode.GetChild(term[j]);
if (item == null)
{
if (j + 1 < term.Length)
{
item = new TreeNodeMiddle();
}
else
{
item = new TreeNodeEnd(term, pParent1, pParent2, _lastTreeNode, _count);
_lastTreeNode = (TreeNodeEnd)item;
_count++;
}
pCurrNode.AddChild(item, term[j]);
}
if (item is TreeNodeMiddle) pCurrNode = (TreeNodeMiddle)item;
}
}
//Поиск последовательностей с одним отличием от заданной не рекурсивным способом
public void SearchDiff1(TreeNodeEnd x1, Dictionary<int, TreeNodeEnd> result)
{
result.Clear();
TreeNodeMiddle pCurrNode = rootNode;
Dictionary<int, TreeNodeMiddle> OneDiffNodesList = new Dictionary<int, TreeNodeMiddle>();
for (int iPos = 0; iPos < x1.Term.Length; iPos++)
{
char cSymbol = x1.Term[iPos];
if (pCurrNode != null)
{
if (cSymbol != '*')
{
TreeNodeBase item = pCurrNode.GetChild(cSymbol == '0' ? '1' : '0');
if (item != null)
{
if (item is TreeNodeMiddle)
{
OneDiffNodesList.Add(iPos, (TreeNodeMiddle)item);
}
else //if (item is TreeNodeEnd)
{
//Добавление терма в выходной список
result.Add(iPos, (TreeNodeEnd)item);
}
}
}
TreeNodeBase pNextNode = pCurrNode.GetChild(cSymbol);
if ((pNextNode != null) && (pNextNode is TreeNodeMiddle))
{
pCurrNode = (TreeNodeMiddle)pNextNode;
}
}
//Проверяются последовательности, отобранные на предыдущих позициях,
//на единственность отличия от заданной
for (int iKey = 0; iKey < iPos; iKey++)
{
if (!OneDiffNodesList.ContainsKey(iKey)) continue;
TreeNodeMiddle pValue = OneDiffNodesList[iKey];
TreeNodeBase item = pValue.GetChild(cSymbol);
if (item == null)
{
OneDiffNodesList.Remove(iKey);
}
else if (item is TreeNodeMiddle)
{
OneDiffNodesList[iKey] = (TreeNodeMiddle)item;
}
else //if (item is TreeNodeEnd)
{
//Добавление терма в выходной список
result.Add(iKey, (TreeNodeEnd)item);
}
}
}
}
}
/// <summary>
/// Базовый интерфейс узла дерева термов
/// </summary>
public interface TreeNodeBase
{
//Очистка выделенных ресурсов
void Clear();
}
/// <summary>
/// Конечный узел дерева термов
/// </summary>
public class TreeNodeEnd : TreeNodeBase
{
//Терм, сопоставленный узлу
private char[] _term;
public char[] Term
{
get { return _term; }
}
//Ссылка на предыдущий конечный узел дерева текущего уровня для одностороннего связанного списка
private TreeNodeEnd _prev;
public TreeNodeEnd Prev
{
get { return _prev; }
}
//Ссылка на родительский конечный узел дерева предыдущего уровня
private TreeNodeEnd _parent1;
public TreeNodeEnd Parent1
{
get { return _parent1; }
}
//Ссылка на родительский конечный узел дерева предыдущего уровня
private TreeNodeEnd _parent2;
public TreeNodeEnd Parent2
{
get { return _parent2; }
}
//Номер узла, который он имеет в последовательности всех конечных узлов текущего уровня
public readonly int Number;
//Конструктор
public TreeNodeEnd(char[] pTermRef, TreeNodeEnd pParent1, TreeNodeEnd pParent2,
TreeNodeEnd pPrevTreeNode, int iNumber)
{
pTermRef.CopyTo(_term = new char[pTermRef.Length], 0);
_parent1 = pParent1;
_parent2 = pParent2;
_prev = pPrevTreeNode;
Number = iNumber;
}
//Очистка выделенных ресурсов
public void Clear()
{
_term = null;
_parent1 = null;
_parent2 = null;
_prev = null;
}
}
/// <summary>
/// Промежуточный узел дерева термов
/// </summary>
public class TreeNodeMiddle : TreeNodeBase
{
//Дочерние узлы
private TreeNodeBase Childs0;
private TreeNodeBase Childs1;
private TreeNodeBase Childs2;
//Очистка выделенных ресурсов
public void Clear()
{
if ((Childs0 != null) && (Childs0 is TreeNodeMiddle)) ((TreeNodeMiddle)Childs0).Clear();
if ((Childs1 != null) && (Childs1 is TreeNodeMiddle)) ((TreeNodeMiddle)Childs1).Clear();
if ((Childs2 != null) && (Childs2 is TreeNodeMiddle)) ((TreeNodeMiddle)Childs2).Clear();
Childs0 = Childs1 = Childs2 = null;
}
//Получение дочернего узла
public TreeNodeBase GetChild(char cSymbol)
{
switch (cSymbol)
{
case '0':
return Childs0;
case '1':
return Childs1;
case '*':
return Childs2;
}
return null;
}
//Добавление дочернего узла
public void AddChild(TreeNodeBase newChild, char cSymbol)
{
switch (cSymbol)
{
case '0':
Childs0 = newChild;
break;
case '1':
Childs1 = newChild;
break;
case '*':
Childs2 = newChild;
break;
}
}
}
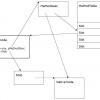
Класс Quine_McCluskey является собственно реализацией этого алгоритма, которому помогают другие классы и интерфейсы: Dnf, TreeNodeBase, TreeNodeMiddle, TreeNodeEnd, TreeFuncTerm. Для запуска оптимизации нужно вызывать один из перегруженных методов Start.
В пункте 1 происходит многократный попарный перебор терм с целью выявления возможности их склейки. Два терма склеиваются, если они отличаются друг от друга значениями только лишь в одной из позиций: у одного стоит ‘0’, а у другого – ‘1’. Склеивающиеся исходные (родительские) термы исключаются из дальнейшей работы, а вместо их двоих далее на следующей итерации п. 1 алгоритма рассматривается новая дочерняя терма, у которой на позиции различающихся переменных родительских терм стоит знак ‘*’. Таким образом, двоичный алфавит входных исходных терм внутри алгоритма расширяется до троичного: ‘0’, ‘1’, ‘*’.
Пункт 1 в классе Quine_McCluskey реализован в процедуре LogicFuncMinimize двумя принципиально разными способами. Первый способ, основанный на 64 битных целочисленных хэш-кодах и поиске в .NET словаре Dictionary<UInt64,…>, работает при количестве входных переменных булевской функции меньше или равном 40, а второй, основанный на поиске в троичном дереве, включается при большем их количестве. Такое раздвоение обусловлено тем, что первый способ работает несколько быстрее, чем второй, поэтому его использование приоритетнее, но он работает корректно только при количестве входных переменных до 40, а при большем их количестве выходит за 64 бит разрядную сетку целочисленного хэш-кода, используемого для работы алгоритма. Действительно, т. к. в термах внутри алгоритма применяется троичная логика, то при количестве входных переменных равном 41 максимальное значение хэш-кода $inline$3^{41}$inline$ уже превышает максимальное значение ($inline$2^{64}$inline$-1), которое можно записать в 64 битную переменную.
Второй способ работы п. 1, работающий при количестве переменных во входных термах больше 40, основан на поисковом троичном дереве терм TreeFuncTerm. Промежуточные узлы дерева реализованы с помощью класса TreeNodeMiddle. Каждый из них может ссылаться максимум на три последующих узла в зависимости от того были ли в дерево добавлены соответствующие термы. Все конечные узлы являются экземплярами класса TreeNodeEnd, глубина до которых от корня у них всех одинакова и равна количеству входных переменных. Каждый конечный узел также имеет ссылку на другой узел TreeNodeEnd, который был добавлен до него, реализуя тем самым однонаправленный связанный список. Такого рода список используется для быстрого перебора всех конечный узлов поискового дерева в процессе их склеивания.
Если в п. 1 для терма не находится другого отличающегося от него только в одной позиции терма, т. е. терм ни с кем не склеивается, то он считается одним из результатов работы п. 1 алгоритма, исключается из дальнейшей работы в нём и поступает на вход пункта 2 работы алгоритма, реализованный в процедуре ReduceRedundancyTerms.
Отбрасывание избыточных терм в ReduceRedundancyTerms осуществляется с помощью алгоритма приближенного решения задачи о покрытии множества подмножествами переменной длины. Покрытие, близкое к кратчайшему даёт алгоритм преобразования таблицы покрытий (ТП), основанный на методе “минимальный столбец–максимальная строка”, который можно посмотреть, например здесь.
Приблизительная логика его работы состоит в следующем:
- Исходная таблица считается текущей преобразуемой ТП, множество строк покрытий – пусто;
- В текущей таблице выделяется столбец с наименьшим числом единиц. Среди строк, содержащих единицы в этом столбце, выделяется одна с наибольшим числом единиц. Эта строка включается в покрытие, текущая таблица сокращается вычеркиванием всех столбцов, в которых выбранная строка имеет единицу;
- Если в таблице есть не вычеркнутые столбцы, то выполняется п. 2, иначе – покрытие построено.
Примечание: При подсчёте числа единиц в строке учитываются единицы в невычеркнуых столбцах.
Для проверки работы алгоритма используются две тестовые функции. Первая процедура позволяет для набора входных переменных количеством N сформировать совокупность терм количеством $inline$2^N$inline$, вычислить случайное значение ЛФ для каждого терма и выгрузить в файл только те термы, для которых соответствующее им значение функции было равно TRUE. После этого проводится проверка правильности работы минимизированной формы функции путём вычисления её значения для каждого терма и сравнения с исходным.
public static void TestQuineMcCluskeyRandom(string sFileName, int iVariableAmount)
{
int iTotalCombines = 1 << iVariableAmount;
ICollection<KeyValuePair<string, bool>> FuncResult = new List<KeyValuePair<string, bool>>(iTotalCombines);
File.Delete(sFileName);
Random rnd = new Random();
int iLogicFuncMask = 0;
while (iLogicFuncMask == 0) iLogicFuncMask = rnd.Next(iTotalCombines);
for (int iCounter = 0; iCounter < iTotalCombines; iCounter++)
{
int iCurValue = iCounter;
string sLine = "";
for (int i = 0; i < iVariableAmount; i++)
{
sLine += (iCurValue % 2).ToString();
iCurValue /= 2;
}
bool bFuncValue = (iCounter & iLogicFuncMask) > 0;
if (bFuncValue)
{
File.AppendAllText(sFileName, sLine + Environment.NewLine);
}
FuncResult.Add(new KeyValuePair<string, bool>(sLine, bFuncValue));
}
//Запуск в работу
DateTime DtStart = DateTime.Now;
Console.WriteLine("Старт - " + DtStart.ToLongTimeString());
Quine_McCluskey Logic = new Quine_McCluskey();
Logic.Start(sFileName);
DateTime DtEnd = DateTime.Now;
TimeSpan Elapsed = DtEnd - DtStart;
Console.WriteLine("Завершение - " + DtEnd.ToLongTimeString());
Console.WriteLine("Длительность - " + String.Format("{0:00}:{1:00}:{2:00}",
Elapsed.Hours, Elapsed.Minutes, Elapsed.Seconds));
//Сравнение результатов
int iErrorsCounter = 0;
foreach (KeyValuePair<string, bool> kvp in FuncResult)
{
if (Logic.Result.Calculate(kvp.Key.ToArray()) != kvp.Value) iErrorsCounter++;
}
Console.WriteLine("Кол-во термов = " + Logic.Result.Terms.Count);
Console.WriteLine("Кол-во ошибок = " + iErrorsCounter);
Console.ReadLine();
}
Вторая тестовая процедура позволяет из файла загрузить наборы, записанные предыдущей тестовой функцией TestQuineMcCluskeyRandom, для которых булевская процедура должна принимать значения TRUE и провести проверку правильности работы минимизированной функции.
public static void TestQuineMcCluskeyFile(string sFileName, int iVariableAmount)
{
int iTotalCombines = 1 << iVariableAmount;
ICollection<KeyValuePair<string, bool>> FuncResult = new List<KeyValuePair<string, bool>>(iTotalCombines);
string sFileContent = File.ReadAllText(sFileName);
for (int iCounter = 0; iCounter < iTotalCombines; iCounter++)
{
int iCurValue = iCounter;
string sLine = "";
for (int i = 0; i < iVariableAmount; i++)
{
sLine += (iCurValue % 2).ToString();
iCurValue /= 2;
}
bool bFuncValue = sFileContent.Contains(sLine + Environment.NewLine);
FuncResult.Add(new KeyValuePair<string, bool>(sLine, bFuncValue));
}
//Запуск в работу
DateTime DtStart = DateTime.Now;
Console.WriteLine("Старт - " + DtStart.ToLongTimeString());
Quine_McCluskey Logic = new Quine_McCluskey();
Logic.Start(sFileName);
DateTime DtEnd = DateTime.Now;
TimeSpan Elapsed = DtEnd - DtStart;
Console.WriteLine("Завершение - " + DtEnd.ToLongTimeString());
Console.WriteLine("Длительность - " + String.Format("{0:00}:{1:00}:{2:00}",
Elapsed.Hours, Elapsed.Minutes, Elapsed.Seconds));
//Сравнение результатов
int iErrorsCounter = 0;
foreach (KeyValuePair<string, bool> kvp in FuncResult)
{
if (Logic.Result.Calculate(kvp.Key.ToArray()) != kvp.Value) iErrorsCounter++;
}
Console.WriteLine("Кол-во термов = " + Logic.Result.Terms.Count);
Console.WriteLine("Кол-во ошибок = " + iErrorsCounter);
Console.ReadLine();
}
При тестировании реализации алгоритма Мак-Класки выявлен её существенный недостаток, заключающийся в том, что при количестве входных переменных в термах более или равном 16 работа программы завершается в связи с нехваткой памяти в процедуре Skleivanie на строках:
X2Tree.Add(iCode, new TreeNodeEnd(x1.Value.Term, x1.Value, pSkleivNode, null, X2Tree.Count));
X2Tree.AddTerm(x1.Term, x1, kvp.Value);
Причём эта проблема возникает при работе как по первому, так и по второму варианту работы пункта 1 соответственно порядку строк выше, которые кратко описаны в начале статьи.
Однако следует заметить, что проблема нехватки памяти возникает только в том случае, если оптимизирование происходит на наборе входных терм размером несколько меньше максимального количества $inline$2^N$inline$, где N – количество переменных. Если же используется сокращённый (неполный) набор с количеством Q < Qпор < $inline$2^N$inline$, то проблема не возникает до той поры, пока размер входного набора данных не перерастёт некоторый порог Qпор, критичный для алгоритма.
В качестве возможных путей преодоления этой проблемы исследовалась возможность определения TreeNodeEnd и TreeNodeMiddle не в виде классов языка C#, а в виде структур. Но в связи с принципиальным отличием между классами и структурами, состоящая в том, что нельзя получить ссылку на структуру, этот путь оказался тупиковым вследствие того, что исследуемая реализация в своей работе опирается именно на ссылки к TreeNodeEnd и TreeNodeMiddle.
Другим направлением преодоления проблемы с памятью было максимальная очистка памяти сборщиком мусора перед каждой итерацией в внутри п. 1, где и происходит чрезвычайное потребление памяти. Для этого в код функции LogicFuncMinimize были добавлены явные вызовы сборщика мусора (garbage collector). Выяснилось, что с уборкой мусора время работы значительно меньше, чем без неё! Хотя, казалось бы, на работу сборщика мусора должно тратиться время, что должно было ухудшить результат. Возможное объяснение этого «феномена» заключается в том, что освобождение памяти сборщиком уменьшает её дефрагментацию в куче, что положительно сказывается на скорости поиска свободных участков при последующем её массовом выделении.
Каких-либо иных возможностей на преодоление неприятностей с нехваткой памяти я не вижу. В связи с чем возникает вопрос можно ли что-то изменить, чтобы добиться стабильной работы алгоритма на полном наборе входных терм с количеством переменных хотя бы до 30? Или это врождённое свойство этого алгоритма, которое не поддаётся коррекции?
Тем не менее, несмотря на возможные проблемы с памятью, предложенная реализация алгоритма Мак-Класки в реальных задачах может быть использована в качестве достаточно быстрого и надёжного оптимизатора ЛФ, заданных набором терм своих входных переменных, при которых логическая функция принимает истинное значение, когда количество переменных N<16 или количество терм Q << $inline$2^N$inline$.
Автор: Degun