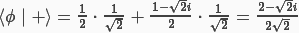Символьные вычисления на примере решения одной несложной задачи по квантовой механике

Сего дня я хотел бы предложить своим читателям небольшую заметку о том, как при помощи языка Haskell разработать модуль для выполнения символьных вычислений. В этой заметке будет описано только самое начало — как подступиться к задаче, какие типы данных использовать, как привязать к решению задачи мощную систему вывода типов языка Haskell. При помощи разработанных программных сущностей мы попробуем решить одну простенькую задачу по квантовой механике или даже, скорее, по линейной алгебре (она взята из первого задания курса «Quantum Mechanics and Quantum Computation» на Coursera — задача № 11). При этом мы посмотрим, как последовательное написание функций для выполнения символьных вычислений позволяет всё ближе и ближе подойти к правильному решению.

Вот условие задачи:

Let |ϕ> = ½ |0> + (1 + √2 i)/2 |1> be the state of a qubit. What is the inner product of |ϕ> and |+>?

Другими словами, необходимо найти скалярное произведение двух векторов, которые представляют кубиты |ϕ> и |+>, причём первый кубит задан в базисе (|0>, |1>), а то, как в этом же базисе раскладывается второй кубит, надо помнить :).

Для решения задачи мы будем пользоваться соглашением о скалярном произведении комплекснозначных векторов, принятом в физике — для этого используется так называемая нотация Дирака. Это значит, что при произведении компонентов векторов, для первого вектора необходимо взять сопряжённые комплексные числа. Но это частность. В общем же нашей задачей является написание общего модуля для решения символьных выражений. Почему символьных? Потому что ответ требуется примерно в таком же виде, в каком задано условие — в виде дробей, невычисленных квадратных корней и т. д.

Модуль решения задачи

Решение задачи на языке Haskell будет оформлено в виде двух модулей. Первый — основной модуль, в котором будут описаны типы данных для описания квантовых состояний и кубитов, функции для манипуляции с ними, а также функция решения задачи — по сути, функция для вычисления скалярного произведения по соглашению, принятому в физике. Во втором модуле, и его мы рассмотрим в следующем разделе, будет описан тип данных для представления символьных выражений, а также все необходимые функции для него. Второй модуль будем описывать итеративно — постепенно наращивая функционал и смотря на то, как меняется при этом решение.

Начнём, как обычно, с определения модуля и импорта:

module Main (main) where

import Control.Arrow ((&&&))
import Data.Complex
import Data.Function (on)
import Data.List (groupBy, sortBy)

import Expression_08

Здесь важным является импорт модуля Expression_08 — это импорт второго нашего модуля, который будет описан позже. И здесь приводится импорт уже восьмой итерации. Поскольку в статье описывается последовательно восемь итераций от 01 до 08, то для внимательного изучения того, что происходит, вдумчивым читателям надо будет вручную исправлять декларацию импорта этого модуля на номер соответствующей итерации. Независимо от номера итерации описываемый в данном разделе модуль не меняется.

Теперь определим алгебраический тип данных (АТД) для представления одного квантового состояния:

data QuantumState a = QS
                      {
                        amplitude :: Complex a,
                        sign      :: String
                      }

В квантовой физике для описания квантовых состояний используется нотация Дирака с этакими прикольными угловыми скобками. У любого квантового состояния есть комплекснозначная амплитуда и некоторое обозначение. Соответственно, наш АТД содержит два поля для представления амплитуды и обозначения. Обозначение имеет тип String на всякий случай — может быть потребуется записывать обозначения сложных состояний связанных кубитов. Функции для работы с комплексными числами возьмём из стандартного модуля Data.Complex.

Здесь надо понимать этот АТД так. Если амплитуда некоторого квантового состояния равна α, а описывающий его символ, к примеру, — «0», то само это квантовое состояние записывается в нотации Дирака как α|0>. Собственно, именно так определим для данного АТД экземпляр класса Show, который позволяет представлять значения АТД в виде строк:

instance (RealFloat a, Show a) => Show (QuantumState a) where
  show (QS a@(r :+ i) s) = ob ++ prettyShowComplex a ++ cb ++ name
    where
      name = "|" ++ s ++ ">"
      ob   = if r /= 0 && i /= 0
               then "("
               else ""
      cb   = if r /= 0 && i /= 0
               then ")"
               else ""

Функция prettyShowComplex реализована взамен стандартной функции show для типа Complex, поскольку стандартный способ отображения комплексных чисел на языке Haskell далёк от канонической записи, принятой в математике. Так что эта функция prettyShowComplex просто реализует канонический способ записи комплексных чисел:

prettyShowComplex :: (RealFloat a, Show a) => Complex a -> String
prettyShowComplex (re :+ im)  | im == 0   = show re
                              | re == 0   = if im < 0
                                              then sign ++ showIm
                                              else showIm
                              | otherwise = show re ++ " " ++ sign ++ " " ++ showIm
  where
    sign | im < 0    = "-"
         | otherwise = "+"
    
    showIm | im == 0   = ""
           | im == 1   = "i"
           | otherwise = show (abs im) ++ "i"

Здесь много всяких условий для того, чтобы приятно для глаз математика записывать разнообразные варианты комплексных чисел — не только «1 + 2i» или «1 — 2i», но и такие особенные варианты, как «0», «1», «i», «-i», «2i», «-2i» и т. д.

Теперь определим тип для представления кубита. Мы будем представлять только дискретные кубиты, то есть такие, у которых имеется конечное число квантовых состояний. Так что кубит — это всего лишь список квантовых состояний. Но мы определим тип, изоморфный списку, поскольку далее для него же определим экземпляр класса Show, который будет отличаться от стандартного определения для списка. Вот это определение:

newtype Qubit a = Qubit
                  {
                    quantumStates :: [QuantumState a]
                  }

Ну и, соответственно, экземпляр класса Show:

instance (RealFloat a, Show a) => Show (Qubit a) where
  show (Qubit qs) | null qs'  = ""
                  | otherwise = fst (head qs') ++ foldl show' "" (tail qs')
    where
      qs' = filter (not . null . fst) $ map (show &&& amplitude) qs

      show' ss (s, r :+ i) = ss ++ " " ++ sign ++ " " ++ part
        where
          (sign, part) = if (i == 0 && r < 0) || (r == 0 && i < 0)
                           then ("-", if head s == '\' then s else tail s)
                           else ("+", s)

Здесь опять сделано много специальных условий для того, чтобы кубиты представлять не просто в виде набора квантовых состояний, а в виде хорошо записанного математического выражения. Для этого знак сложения или вычитания записывается между отдельными квантовыми состояниями: «1/√2|0> + 1/√2|1>» или «1/√2|0> — 1/√2|1>».

Собственно, всё готово для определения главной функции для решения задачи. Опять воспользуемся подходом к разработке сверху вниз и начнём с определения самого верхнего уровня:

main :: IO ()
main = writeFile "Result_08.txt" $ prettyShowComplex $ innerProduct plus phi
  where
    phi :: Qubit (Expression Float)
    phi  = Qubit [QS (Fraction (Number 1) (Number 2) :+ Number 0) "0",
                  QS (Fraction (Number 1) (Number 2) :+ Fraction (Sqrt 2) (Number 2)) "1"]
    
    plus :: Qubit (Expression Float)
    plus = transform (Qubit [QS (Number 1 :+ Number 0) "+"])
                     [("+", Qubit [QS (Fraction (Number 1) (Sqrt 2) :+ Number 0) "0",
                                   QS (Fraction (Number 1) (Sqrt 2) :+ Number 0) "1"])]

Тут всё просто — записать в файл «Result_08.txt» строковое представление результата выполнения функции <code>innerProduct (скалярное произведение) над кубитами plus и phi, которые определены в виде локальных функций. Здесь мы впервые встречаемся с типом Expression, который представляет символьные выражения и будет описан в отдельном модуле, который мы рассмотрим в следующем разделе.

Здесь ещё есть вызов функции transform, которая осуществляет выражение заданного кубита в другом базисе. Её мы рассмотрим позже.

А вот определение функции для вычисления скалярного произведения:

innerProduct :: (Integral a, RealFloat a) => Qubit a -> Qubit a -> Complex a
innerProduct x y = foldl (acc p -> acc + uncurry (*) p)
                         (0 :+ 0)
                         [(ax, conjugate ay) | QS ax sx <- quantumStates x,
                                               QS ay sy <- quantumStates y,
                                               sx == sy]

И опять — ничего сложного нет. При помощи генератора списка мы выбираем все такие пары амплитуд квантовых состояний, при которых символы у обоих кубитов совпадают. Заодно сразу же для второго кубита преобразуем амплитуду в сопряжённое комплексное значение. Далее полученный список сворачивается посредством сложения произведений обоих чисел в каждой паре. В результате получается комплексное число с нулевой мнимой частью. Но мы оставим его комплексным для того, чтобы результат был совместим с другими значениями, которые надо будет вычислять — лишние приведения типов нам тут ни к чему.

Ну а теперь функция перевода кубита в другой базис transform:

transform :: RealFloat a => Qubit a -> [(String, Qubit a)] -> Qubit a
transform (Qubit qs) basis
  = sumQubits [Qubit $ map ((QS a'' s'') -> QS (a'' * a) s'') b' | (QS a s) <- qs,
                                                                    (s', Qubit b') <- basis,
                                                                    s == s']

Данная функция, как было сказано, преобразует заданный кубит в новый базис. Базис описывается при помощи списка пар, где первым элементов пары является символ в изначальном базисе кубита, а вторым — выражение этого символа в новом базисе. Так, к примеру, квантовое состояние |+> выражается в базисе (|0>, |1>) как «1/√2|0> + 1/√2|1>», что, собственно, и записано в определении локальной функции plus в функции main.

Как происходит преобразование? При помощи генератора списка готовится список кубитов, каждый из которых собирается как кубит из базиса, соответствующий символ которого равен какому-либо символу из преобразуемого кубита, при этом амплитуды кубита из базиса и изначального кубита перемножаются. Затем все кубиты в списке складываются специальным образом при помощи функции sumQubits.

Например, для того, чтобы перевести кубит «1/√2|+> + 1/√2|->» в базис (|0>, |1>), необходимо амплитуду при символе «+» (которая равна 1/√2) умножить на выражение этого символа в базисе (|0>, |1>), в результате чего получается «½ |0> + ½ |1>». Ну а выражение символа |-> в том же базисе умножается на его амплитуду, в результате чего получается кубит «½ |0> — ½ |1>». Сложение этих кубитов даёт значение |0>.

Складывать кубиты необходимо так, чтобы сумма квадратов модулей амплитуд при всех символах всегда равнялась единицы. Это условие нормализации, и оно необходимо по той простой причине, что квадрат амплитуды является вероятностью того, что при измерении кубит будет обнаружен в данном состоянии. А поскольку сумма вероятностей для всех квантовых состояний должна равняться 1, то вот такое условие нормализации имеет место. Поэтому определении функции sumQubits выглядит так:

sumQubits :: RealFloat a => [Qubit a] -> Qubit a
sumQubits = normalize .
              Qubit .
              map (((qs, s) -> QS (sum $ map amplitude qs) s) .
                   (qs -> (qs, sign $ head qs))) .
              groupBy ((==) `on` sign) .
              sortBy (compare `on` sign) .
              concatMap quantumStates

Функция хоть и записана в бесточечной форме, но вполне проста. Берём списки квантовых состояний всех кубитов и сливаем их. Затем сортируем при помощи сравнения символов квантовых состояний. После сортировки группируем список квантовых состояний по символам — все амплитуды при одинаковых символах оказываются в одном списке. Затем производится сложение амплитуд при одном и том же символе и развёртывание одного уровня вложенности списка. После этого список квантовых состояний можно обернуть в конструктор Qubit и подвергнуть нормализации. Функция нормализации normalize достаточно проста:

normalize :: RealFloat a => Qubit a -> Qubit a
normalize (Qubit qs) = Qubit $ map ((QS a s) -> QS (a / dnm) s) qs
  where
    dnm = sqrt $ sum $ map (module2 . amplitude) qs

Все амплитуды при каждом квантовом состоянии делятся на одно и то же число dnm, которое как раз и равно квадратному корню из суммы квадратов модулей амплитуд. Квадрат модуля амплитуды вычисляется при помощи функции module2, которая определяется следующим образом:

module2 :: RealFloat a => Complex a -> Complex a
module2 c = c * conjugate c

Лирическое отступление: когда я реализовывал этот модуль (в рамках более глобальной задачи), то в первой реализации функции normalize стоял не вызов функции module2, а вызов функции (^2) (квадрат же). Это породило при вычислении такое многоэтажное математическое выражение, что я долго не мог уснуть после его созерцания. Внезапно молния озарения ударила меня — мы не должны вычислять квадрат комплексного числа, но должны вычислить квадрат модуля его. И выражение сразу стало таким, каким оно должно быть. Кратко об этом написано здесь (осторожно, там немного спойлера).

• Модуль Main для скачивания почтенной публикой: Main.hs.

Модуль символьных вычислений

Символьные вычисления — это аналитические преобразования математических выражений, работа с математическими формулами как с последовательностью символов. Символьные выражения могут содержать числа, но эти числа рассматриваются только как некоторые вычислительные объекты. Обычно манипуляция с символьными выражениями производится именно на уровне формул (упрощения, преобразования и т. д.), а вычисление выражения осуществляется по специальной команде посредством назначения численных значений элементам формул.

Например, символьное выражение (a + b)(a — b) очевидным образом преобразовывается в a² — b², при этом оставаясь именно в таком виде. Если осуществить подстановку вида a ← (x — 1), то выражение преобразуется к виду (x² — 1) — b². И только после подстановок x ← 2 и b ← 1, выражение может быть вычислено, результат чего составит 2.

Именно такую логику работы мы хотим реализовать во втором модуле на языке Haskell для решения нашей задачи. Для этой цели мы постепенно будем наращивать сложность, рассматривая построение этого модуля по шагам. Всего будет восемь итераций, и для каждой итерации будет дан вариант модуля Expression.

Итерация 1

Прежде всего надо определить АТД для представления символьных выражений. Беглое размышление показывает, что в этой задаче для представления символьного выражения достаточно следующего рекурсивного определения:

• Число является символьным выражением.
• Отрицание символьного выражения является символьным выражением.
• Квадратный корень из символьного выражения является символьным выражением.
• Отношение двух символьных выражений является символьным выражением.
• Два символьных выражения, связанных бинарной операцией, являются символьным выражением.
• Других символьных выражений, вроде бы, нет.

Это определение является вполне достаточным для решения поставленной задачи, но откровенно неполным для решения более общих задач. В частности, здесь нет и намёка на какие-либо переменные, нет функциональных символов и т. д. При написании полноценного фреймворка для решения задач по квантовым вычислениям необходимо предусмотреть все возможности. Однако сейчас мы не будем заострять на этом внимания и будем довольствоваться этим определением, которое, кстати, переводится на язык Haskell один в один:

data Expression a
  = Number
    {
      number :: a
    }
  | Negation
    {
      negation :: Expression a
    }
  | Sqrt
    {
      squareRoot :: Expression a
    }
  | Fraction
    {
      numerator   :: Expression a,
      denominator :: Expression a
    }
  | Operation
    {
      operator :: a -> a -> a,
      operandX :: Expression a,
      operandY :: Expression a
    }

Теперь надо подумать — а каким образом мы будем реализовывать арифметику над этим АТД? Да и какая арифметика нам нужна? Ответ на эти вопросы даёт сам язык Haskell. Ведь в нём, в стандартном модуле Prelude уже есть всё необходимое для осуществления математических операций над любыми объектами. Действительно, нам же надо просто реализовать экземпляры всех математических классов для этого АТД, и вуа-ля — модуль заиграет всеми живыми красками, а система типизации языка Haskell сама будет проверять то, как используется тип.

Если посмотреть на систему классов языка Haskell, которые предназначены для выполнения математических действий, т омы увидим довольно внушительную иерархию. Начинается она с классов Eq, Ord и Num, а заканчивается всякими экзотическими классами, которые предоставляют методы для вычисления тригонометрических функций, всяких полярных координат и т. д. И всё это надо реализовать, если мы хотим сделать полноценный фреймворк. Но как подступиться к этой задаче?

На помощь приходит одна важная техника, которая позволяет начать реализацию постепенно. Мы определим заглушки для всех методов всех классов в виде вызова системной функции error, которая выводит на экран заданное сообщение об ошибке и останавливает программу. Это будет выглядеть примерно так:

instance (Eq a, Integral a, Floating a) => Eq (Expression a) where
  (==) = error "Eq.(==)"

Таким образом будут определены все методы для классов Eq, Num, Enum, Real, Ord, Floating, Integral, Fractional, RealFrac и RealFloat. Все эти классы необходимы для решения задачи, но не все методы нужны. Какие методы нужны — поможет узнать только выполнение функции main. Запуская её, мы будем получать сообщения об ошибках, вроде:

Error: Num.(+)

И это позволит шаг за шагом реализовать только те методы, которые потребуются для решения задачи. Зато запускать программу можно будет сразу, поскольку компиляцию она пройдёт — формально все методы всех классов (которых, к слову, требуется аж 71). Ещё, кстати, надо будет реализовать экземпляр класс Integral для типа Float (и мне не понятно, почему этого экземпляра нет в стандартной поставке). Ну и класс Show тоже не надо обходить вниманием, но пока тоже оставим его в виде заглушки.

В общем, смотрите полный код модуля.

• Получить описанный вариант модуля можно по следующей ссылке: Expression_01.hs.

Итерация 2

Теперь нам нужно подумать, как представлять символьные выражения в виде строки, чтобы выводить их на экран. Первое, что приходит в голову, — воспользоваться форматом для формул LaTeX. Простые формулы вполне понятны по своему представлению в этом формате, а для более или менее сложных формул можно воспользоваться каким-либо инструментом визуализации, например, Texify. Поэтому сразу же попробуем написать экземпляр класса Show:

instance (Show a, Eq a, Floating a) => Show (Expression a) where
  show (Number x)           = show x
  show (Negation x)         = '-' : show x
  show (Sqrt x)             = "\sqrt{" ++ show x ++ "}"
  show (Fraction x y)       = "\frac{" ++ show x ++ "}{" ++ show y ++ "}"
  show op@(Operation _ x y) = case operationType op of
                                OTAddition       -> show x ++ " + " ++ show y
                                OTSubtraction    -> show x ++ " - " ++ show y
                                OTMultiplication -> show x ++ " * " ++ show y
                                _                -> "?"

Оказывается, что всё не так просто. В образцах нельзя написать что-то вроде show (Operation (+) x y) = .... Вернее, так написать можно, но любая бинарная функция будет тут же сопоставлена с первым же образцом такого вида. Поэтому для бинарных операций нам придётся написать небольшой костыль — функция operationType будет возвращать одно значение из следующего перечисления:

data OperationType = OTUndefined
                   | OTUnknown
                   | OTAddition
                   | OTSubtraction
                   | OTMultiplication
                   | OTFraction
  deriving Eq

Честно говоря, здесь нам понадобятся только три конструктора. Остальные мы определили на будущее — вдруг ещё что-то потребуется.

Итак, метод show для АТД Expression преобразует символьное выражение в строку в формате LaTeX. Из специальных команд там только frac и sqrt. Остальное выводится как есть. Так что теперь определим функцию operationType. Как назвали её ранее «костылём», такой она и является:

operationType :: (Eq a, Num a, Floating a) => Expression a -> OperationType
operationType (Fraction _ _) = OTFraction
operationType op@(Operation o x y) | o' == x' + y' = OTAddition
                                   | o' == x' - y' = OTSubtraction
                                   | o' == x' * y' = OTMultiplication
                                   | otherwise     = OTUnknown
  where
    o' = evaluate op
    x' = evaluate x
    y' = evaluate y
operationType _ = OTUndefined

Как видно, тут используется самый «грязный хак» — для того чтобы понять, какая бинарная операция используется в символьном выражении, мы вычисляем это выражение и сравниваем его с суммой, разностью и произведением операндов в этом выражении. Для целых чисел это, быть может, и будет нормальным решением. Но для чисел с плавающей точкой из-за вопросов с точностью возможны проблемы. По крайней мере, в разных старых и нелепых языках. Но язык Haskell здесь позволяет прекрасно всё сравнивать — ведь для типа Float определён экземпляр класса Eq, при помощи которого можно всё прекрасно сравнивать, не опасаясь проблем с точностью.

А сама функция evaluate определяется очень уж просто:

evaluate :: Floating a => Expression a -> a
evaluate (Number x)        = x
evaluate (Negation x)      = - evaluate x
evaluate (Sqrt x)          = sqrt $ evaluate x
evaluate (Fraction x y)    = evaluate x / evaluate y
evaluate (Operation o x y) = evaluate x `o` evaluate y

Других изменений в модуль на этой итерации мы не вносили, так что программа при запуске функции main всё также будет выводить сообщение об ошибке при попытке сложить два символьных выражения. Так что скорее перейдём к третьей итерации.

• Получить описанный вариант модуля можно по следующей ссылке: Expression_02.hs.

Итерация 3

Ну а теперь пришло время заняться написанием функций для осуществления математических операций. Для этого будем запускать функцию main, смотреть, какая функция требуется на каждом шаге, и определять эту функцию. В конечном итоге, мы определим все функции, которые нам потребуются для решения задачи.

Как уже писалось, первым сообщением выводится требование реализовать операцию сложения. Не будем мудрствовать лукаво и определим метод (+) так:

  Number x + Number y         = Number (x + y)
  Negation x + Negation y     = Negation (x + y)
  Fraction x y + Fraction z v
    | y == v                  = Fraction (x + z) y
    | otherwise               = Fraction (x * v + z * y) (y * v)
  x + y                       = Operation (+) x y

Можно было, конечно, ограничиться самым последним клозом, но здесь мы уже сразу применили несколько оптимизаций. Ведь сразу понятно, что если складывать два числа, то в результате получится число, а для сложения отношений надо привести их к общему знаменателю.

В итоге нам потребуется определить всего 10 методов:

• Методы (+), (-), (*), negate, abs и fromInteger из класса Num.
• Метод (<) из класса Ord.
• Метод sqrt из класса Floating.
• Метод (/) из класса Fractional.
• Метод scaleFloatиз класса RealFloat.

Все эти методы определяются самым тривиальным образом, примерно так же, как и приведённый пример для операции (+). Более того, для метода scaleFloat сделана заглушка в виде id, поскольку в реальности этот метод не понадобится, а если реализовывать его правильно, то он потянет за собой весь набор методов класса RealFloat, а там мороки на несколько дней разработчика. Так что пока оставим так.

В итоге после тривиальной реализации всех требуемых методов мы даже можем запустить функцию main и получить результат. Размер полученного в результате работы файла составляет 69 Кб, и в полученной формуле очень много сложений с нулями, каких-то странных дробей и т. д. Начало этого файла такое:

0.0 + frac{0.0 + frac{1.0}{sqrt{2.0}} * 1.0 + 0.0 * sqrt{frac{sqrt{0.0 + 0.0 + frac{1.0}{sqrt{2.0}} * 1.0 + ...

Визуализатор формул не смог справиться с ним. Но ничего страшного, всё будет хорошо. Сейчас подумаем и продолжим. А пока можно посмотреть на код и на результат…

• Получить описанный вариант модуля можно по следующей ссылке: Expression_03.hs.
• Посмотреть на невразумительный результат работы функции main можно здесь: Result_03.txt.

Итерация 4

Попробуем немного сократить выражение, получающееся в результате. Для этого внесём в правила вычисления символьных выражений дополнительные условия. Мы же знаем, что прибавление 0 и умножение на 1 не несёт никакого эффекта, а, скажем, вычитание двух одинаковых чисел друг из друга даёт в результате 0. Вот эти правила и опишем, внеся изменения в определения операций (+), (-) и (*):

  Number x + Number y         = Number (x + y)
  x + Negation y | x == y     = Number 0
  Negation x + y | x == y     = Number 0
  Negation x + Negation y     = Negation (x + y)
  Fraction x y + Fraction z v
    | y == v                  = Fraction (x + z) y
    | otherwise               = Fraction (x * v + z * y) (y * v)
  x + y
    | x == Number 0 = y
    | y == Number 0 = x
    | otherwise     = Operation (+) x y
  
  Number x - Number y         = Number (x - y)
  Negation x - Negation y     = Negation (x - y)
  Fraction x y - Fraction z v
    | y == v                  = Fraction (x - z) y
    | otherwise               = Fraction (x * v - z * y) (y * v)
  x - y
    | x == y        = Number 0
    | x == Number 0 = Negation y
    | y == Number 0 = x
    | otherwise     = Operation (-) x y
  
  Number x * Number y         = Number $ x * y
  Negation x * Negation y     = x * y
  Sqrt x * Sqrt y             = Sqrt $ x * y
  Fraction x y * Fraction z v
    | x == v && y == z        = Number 1
    | x == v                  = Fraction z y
    | z == y                  = Fraction x v
    | otherwise               = Fraction (x * z) (y * v)
  x * y                       = Operation (*) x y

В общем, тут кроме сложения с 0 и умножения на 1 определено ещё несколько простейших правил. В итоге, результат выглядит примерно так:

Пришлось специально уменьшить изображение, а то оно выходило за край известной части Вселенной.

• Получить описанный вариант модуля можно по следующей ссылке: Expression_04.hs.

Итерация 5

Если присмотреться к полученному выражению, то станет ясно, что теперь основная проблема заключается в перемножении дробей. Много-много дробей перемножается, а упрощения выражений в этом случае нет. Попробуем дополнить определение операции (*) для случая перемножения дробей. Получится что-то вроде этого:

  Number x * Number y         = Number $ x * y
  Negation x * Negation y     = x * y
  Negation x * y = Negation $ x * y
  x * Negation y = Negation $ x * y
  Sqrt x * Sqrt y             = Sqrt $ x * y
  Fraction x y * Fraction z v
    | x == v && y == z        = Number 1
    | x == v                  = Fraction z y
    | z == y                  = Fraction x v
    | otherwise               = Fraction (x * z) (y * v)
  x * Fraction y z
    | x == z       = y
    | otherwise    = Fraction (x * y) z
  Fraction x y * z
    | y == z       = x
    | otherwise    = Fraction (x * z) y
  x * y
    | x == Number 0 = Number 0
    | y == Number 0 = Number 0
    | x == Number 1 = y
    | y == Number 1 = x
    | otherwise     = Operation (*) x y

Результат не заставил себя ждать — здесь и нашлась точка перелома. Если на графике по оси абсцисс отложить номер итерации (или какую-либо метрику сложности кода), а по оси ординат отложить уровень сложности получаемого математического выражения, то после внесения нескольких исправлений в определение операции (*) сложность выражения падает катастрофически. В итоге мы имеем:

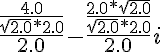
• Получить описанный вариант модуля можно по следующей ссылке: Expression_05.hs.

Итерация 6

Посмотрев на полученное выражение, мы сразу же понимаем, что теперь нам надо заняться упражнением по сокращению дробей. Так что надо будет написать функцию cancel, вызов которой надо будет вызвать перед всеми вызовами конструктора Fraction. Каждый раз, когда у нас появляется дробь, её надо попытаться сократить.

Вот определение функции cancel. Она достаточно нетривиальна:

cancel :: (Floating a, Integral a) => Expression a -> Expression a
cancel f@(Fraction x y)
  | x == Number 0 = Number 0
  | y == Number 1 = x
  | x == y = Number 1
  | isNegation x && isNegation y = let Negation x' = x
                                       Negation y' = y
                                   in  cancel $ Fraction x' y'
  | otx == OTMultiplication &&
    oty == OTMultiplication = let Operation _ x' y' = x
                                  Operation _ z' v' = y
                              in  if x' == z'
                                    then cancel $ Fraction y' v'
                                    else if y' == z'
                                           then cancel $ Fraction x' v'
                                           else if x' == v'
                                                  then cancel $ Fraction y' z'
                                                  else if y' == v'
                                                         then cancel $ Fraction x' z'
                                                         else f
  | otx == OTMultiplication = let Operation _ x' y' = x
                              in  if x' == y
                                    then y'
                                    else if y' == y
                                           then x'
                                           else f
  | oty == OTMultiplication = let Operation _ z' v' = y
                              in  if x == z'
                                    then cancel $ Fraction (Number 1) v'
                                    else if x == v'
                                           then cancel $ Fraction (Number 1) z'
                                           else f
  | otx == OTFraction && oty == OTFraction = let Fraction x' y' = x
                                                 Fraction z' v' = y
                                             in  cancel $ Fraction (x' * v') (y' * z')
  | otx == OTFraction = let Fraction x' y' = x
                        in  cancel $ Fraction x' (y' * y)
  | oty == OTFraction = let Fraction z' v' = y
                        in  cancel $ Fraction (x * v') z'
  | otherwise = f
  where
    otx = operationType x
    oty = operationType y

cancel x = x

Но несмотря на всю свою видимую монструозность, эта функция рассматривает различные варианты дробей и сокращает их. Например, в пятом охранном выражении, там где и числитель, и знаменатель представляют собой произведения, мы последовательно просматриваем, есть ли в числителе и знаменателе одинаковые множители. И если есть, то они просто удаляются (сокращаются). Ну и по остальным охранным выражениям — то же самое. В итоге получается всё очень приятно:

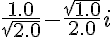
• Получить описанный вариант модуля можно по следующей ссылке: Expression_06.hs.

Итерация 7

Выражение стало практически тем, чем должно быть. Единственная проблема — квадратный корень из квадрата не упрощается. Ну зачем нам лицезреть в выражении «квадратный корень из 1», когда понятно, что это есть 1. Так что теперь в дополнение к функции сокращения дробей необходимо написать функцию для упрощения выражений с квадратным корнем. Само собой разумеется, что её всё так же надо будет вставить во все места, где вызывается конструктор Sqrt. То есть как только у нас появляется корень, мы пытаемся его упростить.

Вот определение:

simplify :: (Floating a, Integral a) => Expression a -> Expression a
simplify s@(Sqrt x)
  | operationType x == OTMultiplication = let Operation _ x' y' = x
                                          in  if x' == y'
                                                then x'
                                                else s
  | operationType x == OTFraction = let Fraction x' y' = x
                                    in  cancel $ (Fraction `on` (simplify . Sqrt)) x' y'
  | isNumber x = let x' = number x
                     r' = root x'
                 in  if r'^2 == x'
                       then Number r'
                       else s
  | otherwise = s
  where
    root n = last $ takeWhile (i -> i^2 <= n) [1..]

simplify x = x

Тут имеют место три типа упрощения. Для начала, если под корнем стоит произведение двух одинаковых чисел, то вместо этого оставляется просто это число. Далее — дробь под корнем преобразуется в дробь корней, каждый из которых подвергается тому же упрощению. Ну и, наконец, если у нас под корнем простое число, то мы проверяем, является ли оно квадратом натурального числа. И если да, то вычисляется корень. Остальные варианты символьных выражений возвращаются этой функцией, как есть.

В итоге получается такое выражение, и это уже окончательное решение задачи в канонической форме:

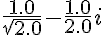
• Получить описанный вариант модуля можно по следующей ссылке: Expression_07.hs.

Итерация 8

Наконец, осталось только изменение, связанное с эстетикой. Наблюдать нули после запятой совсем неинтересно — зачем они нужны, если число целое? Вот и перепишем слегка один из клозов функции show для АТД Expression:

  show (Number x) = if round x == ceiling x
                      then show $ round x
                      else show x

Это позволит получить такое выражение, и оно хорошо:

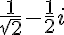
• Получить описанный вариант модуля можно по следующей ссылке: Expression_08.hs.

Заключение

Курс по квантовым вычислениям на Coursera крайне занятный. И большинство упражнений в нём можно решить при помощи развитого фреймворка для символьных вычислений, соединённого с модулей, описывающим понятия предметной области. Вместо того, чтобы считать карандашом на листе бумаги, можно быстро написать функции для расчёта по различным задачам и получать ответы в удобочитаемой форме.

Представленная работа является всего лишь прелюдией к довольно мощному фреймворку, который позволил мне с успехом завершить курс и получить высокую оценку. Конечно, тот фреймворк, который получен в результате работы, намного более мощен и развит, нежели модуль Expression, который описан здесь. В частности:

1. Намного более глубоко проведена работа по сокращению дробей, упрощению выражений, расчётам и преобразованиям.
2. В состав символьных выражений внедрены переменные и функциональные символы, а понимание видов операций и функций сделано через строковые идентификаторы.
3. Описаны многие понятия квантовой механики в общем и квантовых вычислений в частности.
4. Всё это дело оформляется и готовится к публичному выпуску в виде отдельной библиотеки.

Всех читателей, как обычно, благодарю за внимание к моей статье. Если у кого-либо найдутся слова для комментариев, буду рад и всякому отвечу.

Мои предыдущие статьи на Хаброхабре про язык Haskell:

• Генерация естественно-языковых фраз при помощи языка Haskell на основе порождающих грамматик и расширенных цепей Маркова
• Реализация конструирования N-грамм и генерации псевдо ЕЯ-текста на их основе на языке Haskell
• Фреймворк для генерации рекурсивных сказок на языке Haskell
• Утилита для работы с N-граммами
• Решение (несложных) криптографических задач на языке Haskell
• Поиграем в слова: создаём бота-игрока на языке Haskell

Автор: Darkus

Источник