Что мы знаем о ландшафте функции потерь в машинном обучении?

TL;DR

1. В глубоких нейронных сетях основным препятствием для обучения являются седловые точки, а не локальные минимумы, как считалось ранее.
2. Большинство локальных минимумов целевой функции сконцентрированы в сравнительно небольшом подпространстве весов. Соответствующие этим минимумам сети дают примерно одинаковый loss на тестовом датасете.
3. Сложность ландшафта увеличивается по приближении к глобальному минимуму. Почти во всём объёме пространства весов подавляющая часть седловых точек имеет большое количество направлений, по которым из них можно сбежать. Чем ближе к центру кластера минимумов, тем меньше «направлений побега» у встреченных на пути седловых точек.
4. Всё ещё неясно, как найти в подпространстве минимумов глобальный экстремум. Похоже, что это очень сложно; и не факт, что типичный глобальный минимум намного лучше типичного локального.
5. В сгустке минимумов существуют особые кривые, соединяющие локальные минимумы. Функция потерь на этих кривых принимает лишь чуть большие значения, чем в самих минимумах.
6. Некоторые исследователи считают, что широкие минимумы (с большим радиусом «ямы» вокруг) лучше узких. Но есть и немало учёных, которые полагают, что связь ширины минимума с обобщающей способностью сети очень слаба.
7. Skip connections делают ландшафт более дружелюбным для градиентного спуска. Похоже, что вообще нет причин не использовать residual learning.
8. Чем шире слои в сети и чем их меньше (до определённого предела), тем глаже ландшафт целевой функции. Увы, чем более избыточна параметризация сети, тем больше нейросеть подвержена переобучению.

Всё, листайте дальше. Я даже КДПВ ставить не буду.

Статья состоит из трёх частей: обзор теоретических работ, обзор научных работ с экспериментами и перекрёстное сравнение. Первая часть немного суха, если заскучаете, проматывайте сразу к третьей.

Обзор теоретических работ

Как известно, обучение нейронной сети — это поиск минимума целевой функции потерь в пространстве весов . Увы, нахождение глобального минимума произвольной дифференцируемой функции относится к классу NP-сложных задач[1]. Кроме того, нейросети могут иметь очень разную архитектуру и принимать на вход любые данные, так что на глубокий анализ одной формулы с чётко заданными ограничениями надеяться не приходится. Функция невероятно многомерная, следовательно и метод грубой силы тут тоже применить нетривиально. Тем не менее, даже какие-то общие факты о типичном ландшафте могут принести немалую пользу: как минимум, задать общее направление практических исследований.

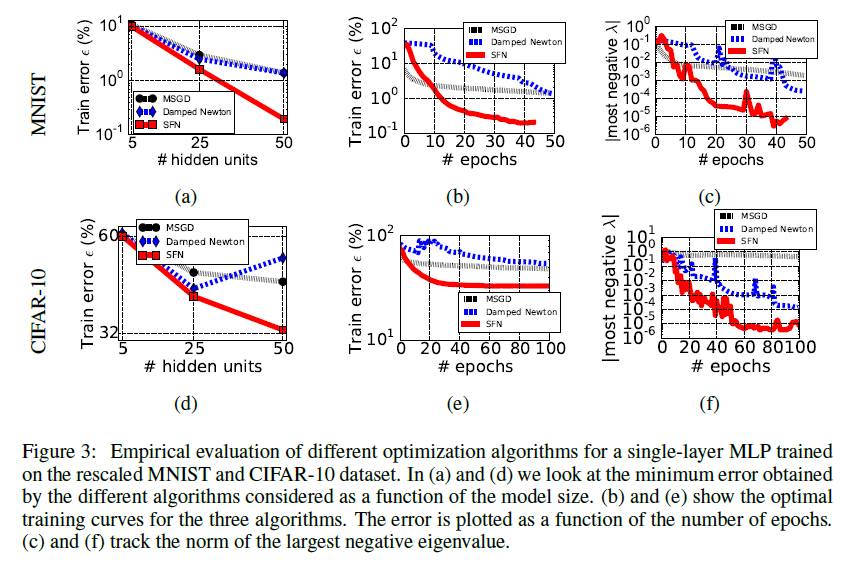
До недавнего времени желающих заняться такой титанической задачей было немного, но в начале 2014 увидела свет статья Andrew Saxe и остальных[2], в которой рассуждается о нелинейной динамике обучения линейных нейронных сетей (приводится формула для оптимальной скорости обучения) и о наилучшем способе их инициализации (ортогональные матрицы). Авторы получают интересные выкладки исходя из разложения произведения весов сети в SVD и теоретизируют, как результаты можно перенести на нелинейные сети. Хоть работа Saxe не имеет прямого отношения к теме этой статьи, она побудила других исследователей глубже вглядеться в динамику обучения нейросетей. В частности, чуть позже в 2014 году Yann Dauphin и команда[3] обозревают существующую литературу по динамике обучения и обращают внимание не только на статью Saxe, но и на работу Bray и Dean[4] из 2007 года про статистики критических точек в случайных гауссовых полях. Они предлагают модификацию метода Ньютона (Saddle Free Newton, SFN), которая не только лучше сбегает из седловых точек, но и не требуют вычисления полного Гауссиана (минимизация идёт по векторам так называемого подпространства Крылова). В статье демонстрируются весмьа симпатичные графики улучшения точности сети, а значит SFN что-то делает правильно. Статья Dauphin, в свою очередь, даёт толчок новым исследованиям распределения критических точек в пространстве весов.

Итак, есть несколько направлений анализа заявленной задачи.

Первый — стащить у кого-нибудь немного обкатанной математики и приложить к собственной модели. Такой подход с невероятным успехом применили Anna Chromanska и команда[5][6], использовав уравнения теории спиновых стёкл. Они ограничились рассмотрением нейросетей со следующими характеристиками:

• Сети прямого распространения.
• Глубокие сети. Чем больше весов, тем лучше работают асимптотические приближения.
• ReLU активационные функции.
• L2 или Hinge функция потерь.

После чего наложили на модель несколько более-менее реалистичных ограничений:

1. Вероятность того или иного нейрона быть активным описыватся распределением Бернулли.
2. Пути активации (какой нейрон активирует какой) равномерно распределены.
3. Количество весов избыточно для формирования функции распределения . Нет таких весов, удаление которых блокирует обучение или предсказание.
4. Сферическое ограничение на веса: (где — количество весов в сети)
5. Все входные переменные имеют нормальное распределение с одинаковой дисперсией.

И несколько нереалистичных:

1. Пути активации в нейронной сети не зависят от конкретного .
2. Входные переменные не зависят друг от друга.

На основании чего получили следующие утверждения:

• Минимумы функции потерь в нейронной сети формируют кластер в сравнительно небольшом подпространстве весов. За некоторой границей значения функции потерь их количество начинает экспоненциально убывать.
• Для правильно обученных глубоких нейронных сетей большинство локальных минимумов примерно одинаковы в плане показателей на тестовой выборке.
• Вероятность оказаться в «плохом» локальном минимуме заметна при работе с маленькими сетями и экспоненциально убывает с увеличением количества параметров в сети.
• Пусть — количество отрицательных собственных значений гессиана в седловой точке. Чем он больше, тем больше путей, по которым градиентный спуск может сбежать из критической точки. Для каждого существует некоторый показатель значения целевой функции , начиная с которого плотность седловых точек с таким начинает экспоненциально убывать. Эти числа строго возрастают. По-русски это означает, что у функции потерь слоёная структура, и чем ближе мы к глобальному минимуму, тем больше будет гадких седловых точек, из которых сложно выбраться.

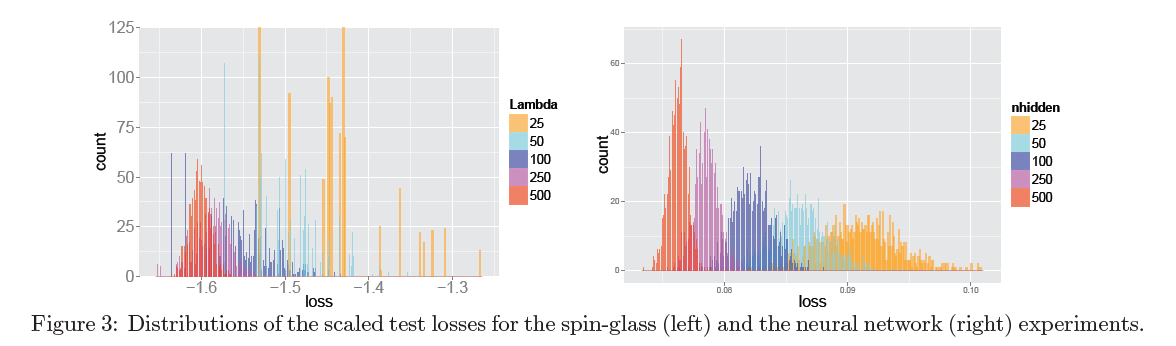
С одной стороны, мы почти «бесплатно» получили много проверенных теорем, показав, что при определённых условиях нейронные сети ведут себя сообразно спиновым стёклам. Если что и способно вскрыть печально известную «чёрную коробку» нейросетей, так это матан из квантовой физики. Но есть и очевидный недостаток: очень сильные исходные посылки. Даже 1 и 2 из группы реалистичных мне кажутся сомнительными, что уж там говорить про группу нереалистичных. Самым серьёзным ограничением в модели мне кажется равномерное распределение путей активации. Что если какая-то маленькая группа путей активации ответственна за классификацию 95% элементов датасета? Получается, она формирует как бы сеть в сети, что в разы уменьшает эффективную .

Есть дополнительный подвох: утверждения Chromanska сложнофальсифицируемы. Не так уж сложно сконструировать пример весов, представляющих «плохой» локальный минимум[7], но это как бы и не противоречит посылу статьи: их утверждения должны выполняться для больших сетей. Однако даже предоставленный набор весов для в меру глубокой feed-forward сети, который плохо классифицирует, скажем, MNIST вряд ли составит сильное доказательство, ведь авторы утверждают, что вероятность встретить «плохой» локальный минимум стремится к нулю, а не что их нет совсем. Плюс, «для правильно обученных глубоких нейронных сетей» — довольно растяжимое понятие…

Второй подход предполагает построение модели самой простой из возможных нейросетей и её итеративное доведение до состояния, когда она может описать современных монстров машинного обучения. Базовая модель у нас давно есть — это линейные нейронные сети (т.е. сети с функцией активации ) с одним скрытым слоем. Они хорошо поддаются анализу, и ими давно занимаются, но результаты этих теоретических изысканий были мало кому интересны, так как в целом линейные сети не слишком полезны.

По крайней мере, были мало кому интересны до недавнего времени. Используя довольно слабые ограничения на размеры слоёв и свойства данных, Kenji Kawaguchi[8] развивает результаты работы [9] аж из 1989 года и показывает, что в определённых линейных нейронных сетях с L2-лоссом

1. Хоть невыпуклая и невогнутая
2. В ней только один глобальный минимум.
3. А все остальные критические точки — седловые
4. Если — седловая точка функции потерь и ранг матричного произведения весов сети равен рангу самого узкого слоя в нейросети, то гессиан в имеет по крайней мере одно отрицательное собственное значение.

После этого Kawaguchi берёт в рассмотрение сети c ReLu-активацией, немного ослабляет ограничения Choromanska[6], и доказывает те же утверждения для нейронных сетей с ReLu-нелинейностями и L2-лоссом. (В следующей работе [10] тот же автор приводит более простое доказательство). Hardt & Ma[11], вдохновлённые выкладками [8] и успехом residual learning, доказывают ещё более сильные утверждения для линейных сетей со skip connections: при определённых условиях в них даже нет «плохих» критических точек без отрицательных собственных значений гессиана (см. [12] для теоретического обоснования, почему «короткие замыкания» в сети улучшают ландшафт, и [13] для примеров графиков до и после добавления skip connection'ов).

Накопленный багаж знаний обобщает совсем недавно появившаяся работа Yun, Sra & Jadbabaie [14]. Авторы усиливают теоремы Kawaguchi и, подобно Chromanska, разделяют пространство весов линейной нейронной сети на подпространство, которое содержит только седловые точки, и подпространство, которое содержит только один глобальный минимум (приводятся необходимые и достаточные условия). Более того, учёные наконец делают шаг в интересующую нас сторону и доказывают похожие утверждения для нелинейных нейронных сетей. Пусть последнее делается и с очень сильными предпосылками, но это предпосылки отличные от условий Chromanska.

Обзор работ с визуализацией

Третий подход — анализ значений гессиана в процессе обучения. Математикам давно известны методы оптимизации второго порядка. Специалисты по машинному обучению периодически заигрывают с ними (с методами, не с математиками… хотя и с математиками тоже), но даже усечённые алгоритмы спуска второго порядка никогда не были особо популярными. Основная причина этого кроется в затратности подсчёта данных, необходимых для спуска с учётом второй производной. Честно вычисленный гессиан занимает квадрат от количества весов памяти: если в сети миллион параметров, то в матрице вторых производных их будет . А ведь ещё хочется как-то посчитать собственные значения этой матрицы…

По той же причине мало и работ, позволяющих посмотреть на динамику изменения гессиана в процессе обучения. Точнее, я нашёл ровно одну работу Yann LeCun и компании[34], посвящённую именно этому, да и то они работают со сравнительно примитивной сетью. Плюс, в работах [3] и [12] есть пара релевантных замечаний и графиков.

LeCun[34]: Гессиан почти полностью состоит из нулевых значений на протяжении всего обучения. В течение оптимизации гистограмма гессиана ещё больше сжимается к нулю. Ненулевые значения распределены неравномерно: в положительную сторону выбрасывается длинный хвост, тогда как отрицательные значения сконцентрированы около нуля. Часто нам лишь кажется, что обучение остановилось, тогда как мы всего лишь оказались в бассейне с маленькими градиентами. В точке останова присутствуют отрицательные собственные значения гессиана.

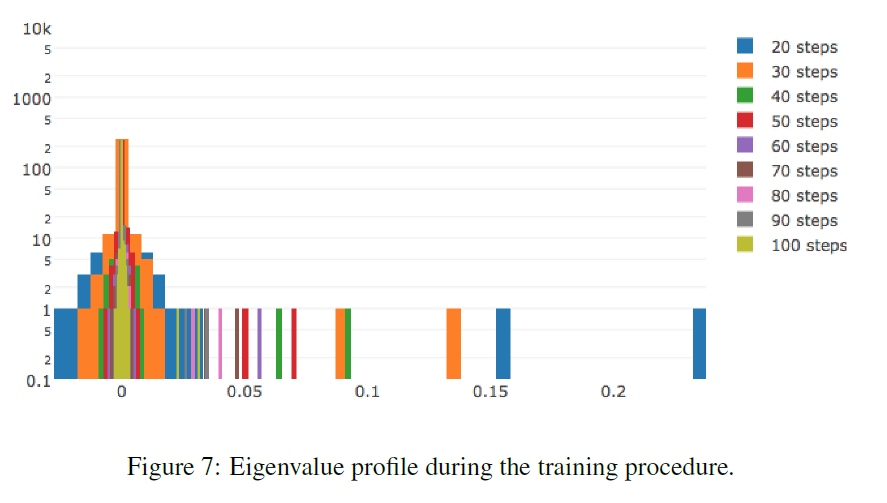
Чем сложнее данные, тем более вытянут положительный хвост распределения собственных значений.

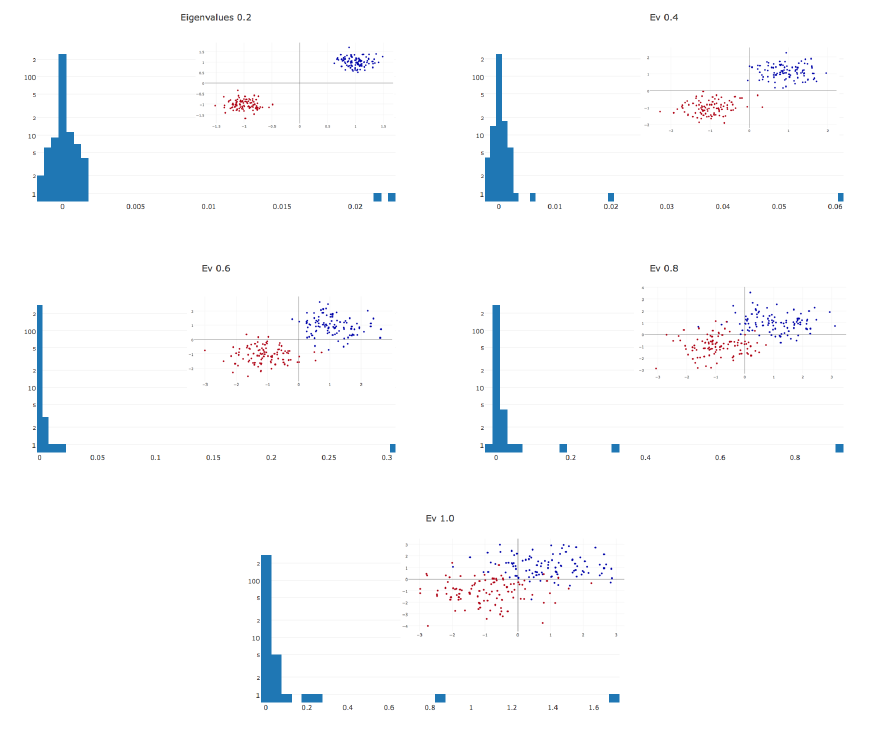
Чем больше параметров в сети, тем более растянута гистограмма собственных значений в обе стороны.

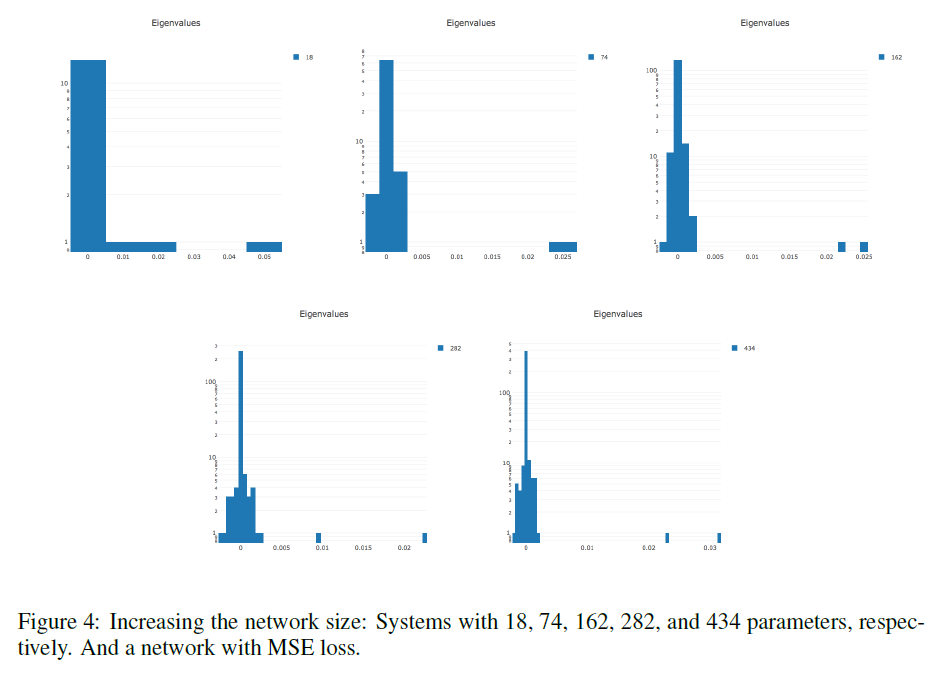
Dauphin et al.[3]: На графиках A и C по оси отложена относительная часть отрицательных значений в критической точке, в которой остановилось обучение, по отложена ошибка на тренировочной выборке. На графиках B и D представлены гистограммы собственных значений матрицы вторых производных для трёх точек с графиков A и C соответственно. Обратите внимание, что они согласуются с гистограммами LeCun.

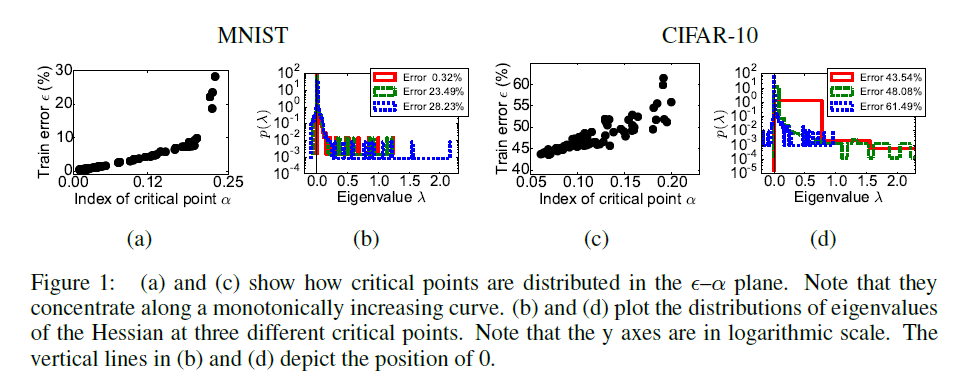
Явно видна корреляция между количеством направлений побега из седловой точки и качеством работы сети в ней.

Orhan&Pitkow[12]: Показаны относительное количество вырожденных и отрициательных собственных значений гессиана. В статье говорится не совсем про то же, о чём в [3] и [34], но в целом графики косвенно подтверждают результаты двух предыдущих работ.

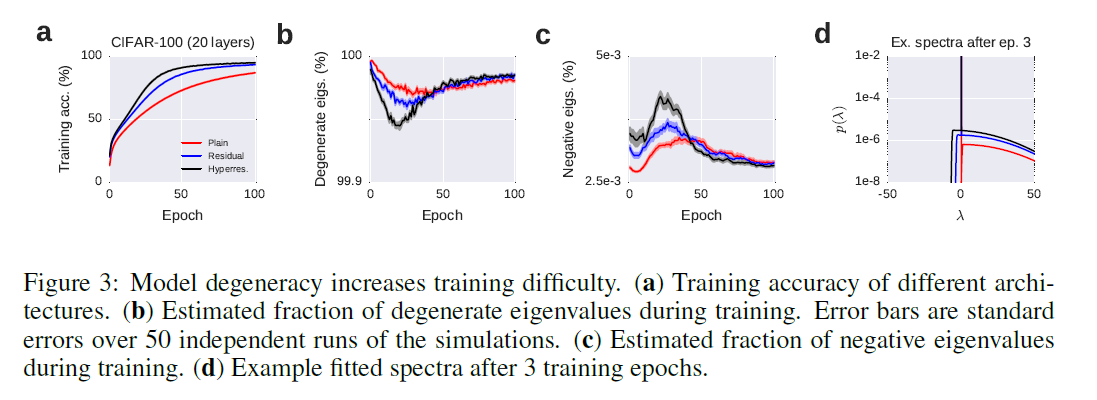
Четвёртый путь — прямой анализ ландшафта при помощи визуализаций каких-либо проекций. Идея тривиальна, но, как уже упоминалось, применить её совсем не просто, ведь в могут быть миллионы весов. Обычно рассматривают два вида визуализаций: значения функции потерь при изменении в пространстве весов по какой-либо кривой и график функции потерь в окрестности какой-либо точки при , где и — некоторые векторы, задающие плоскость сечения пространства весов. В случае одномерной проекции обычно визуализируют переходы из изначального состояния сети в конечное (напрямик или по кривой обучения) или между двумя конечными состояниями; в двумерном состоянии обычно берут два наиболее значимых вектора в PCA-разложении конечного участка кривой обучении. Кроме многомерности проблема визуализации целевой функции осложняется тем, что по сути одинаковые минимумы могут иметь очень разные веса. Например, если в линейной нейронной сети веса в одном слое уменьшить в раз, а в следующем за ним — в раз увеличить, то получившиеся наборы весов и области пространства вокруг них будут сильно отличаться, тогда как выученные фичи будут по сути одними и теми же. Дополнительное измерение для анализа — тип минимизатора или параметры конкретного типа минимизатора, с которыми был получен .

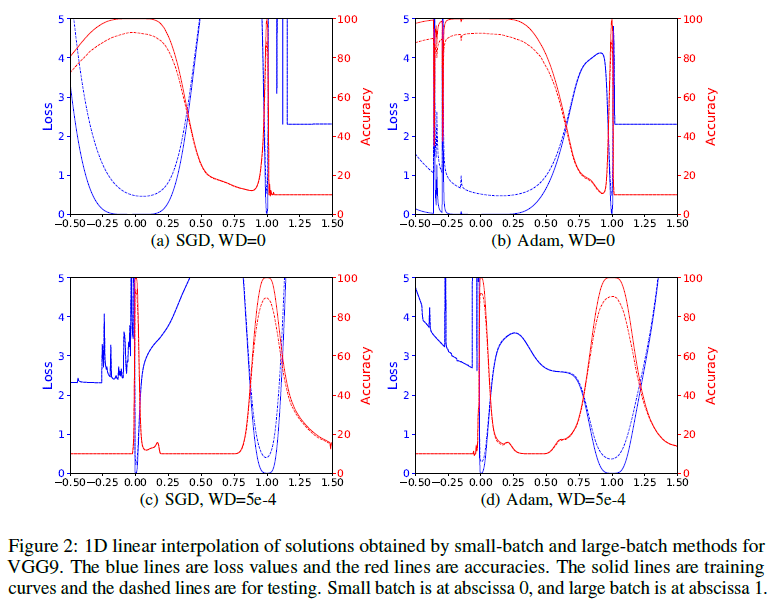
Одной из таких работ является [16]. В ней исследователи смотрят на отрезок между конечными точками запусков с SGD, Adam, Adadelta и RMSProp. Как и во многих других работах обнаруживается, что различные алгоритмы находят характерно разные минимумы. Также авторы статьи показывают, что если во время обучения поменять тип алгоритма, то изменит курс к другому минимуму. В качестве второго бонуса исследователи, смотрят как повлияет на ландшафт между конечными точками batch normalization, и заключают, что, во-первых, с batch normalization качество полученного минимума намного меньше зависит от точки инициализации, а во-вторых, между конечными в ландшафте целевой функции возникают «стены» — узкие участки с очень большим значением (непонятно, откуда это берётся и что с этим делать). В любом случае, на приведённых графиках между минимумами видны «холмы» loss'а, но никак не какая-то сложная поверхность.

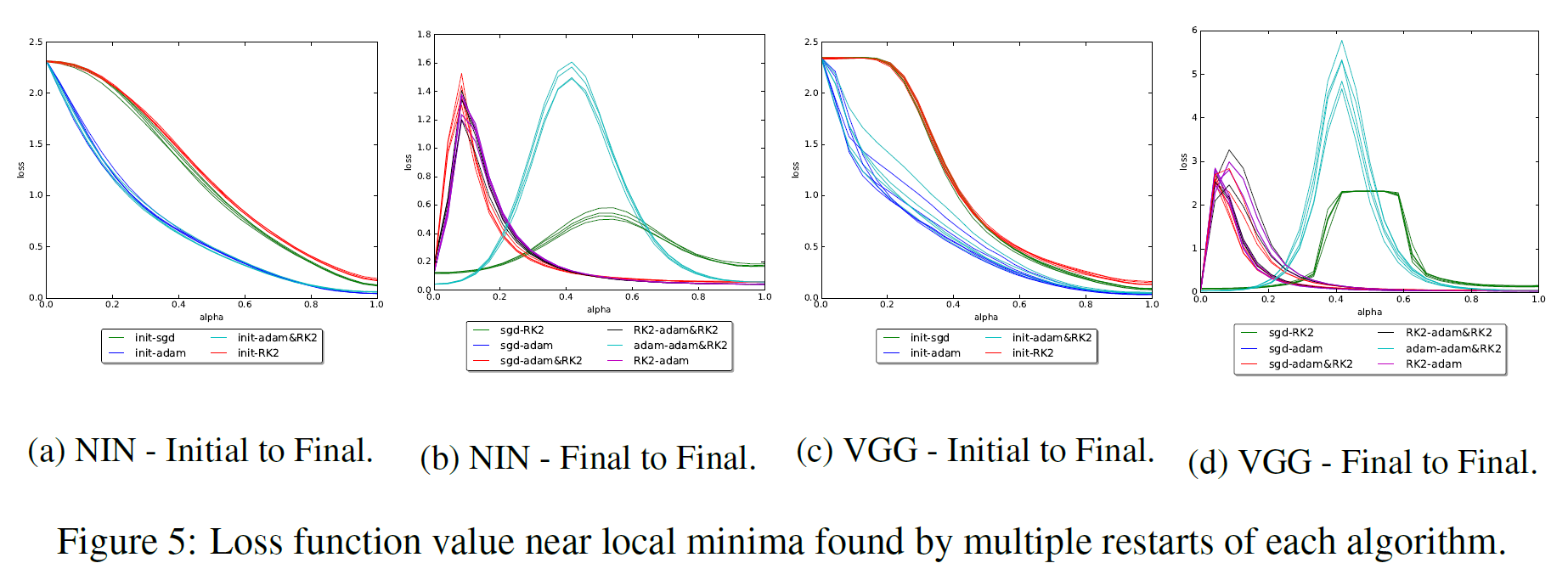
Сейчас нас больше интересует группа исследований, в которых доказывается, что между двумя минимумами в пространстве весов и почти всегда можно провести некоторую кривую, на всём протяжении которой функция потерь не будет превышать для , отделённых от нуля некоторой границей, но значительно меньших типичных значений функции потерь[17][18][19]. Есть сразу несколько способов сформировать такую кривую: как правило, в них простой отрезок между и разбивается на звенья, после чего соединяющие их узлы градиентным спуском перемещааются в пространстве весов. С помощью таких кривых можно, например, собирать более качественнын ансамбли сетей[18]. Их результаты показывают, что кластер минимумов имеет «пористую» структуру.

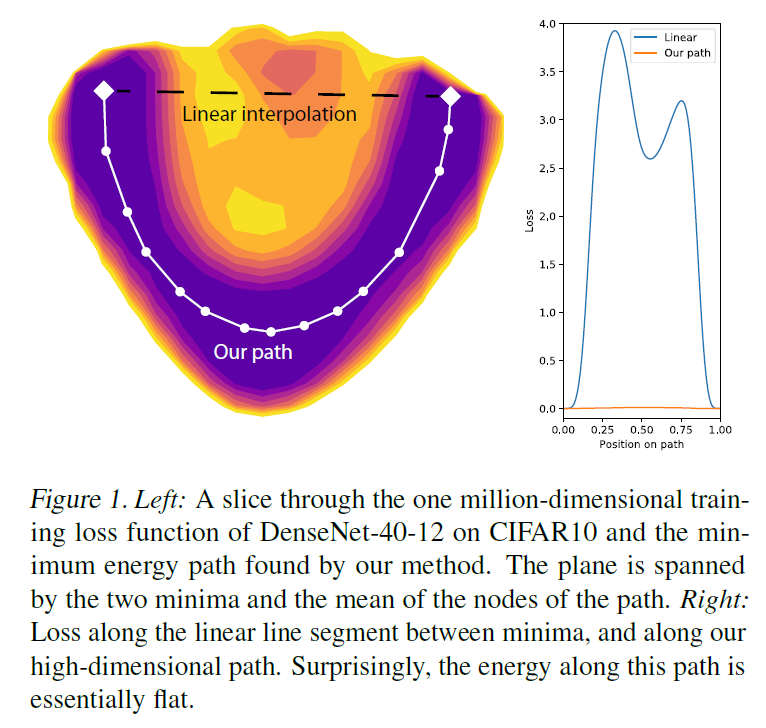
В ту же копилку идёт совсем недавняя статья от интернациональной команды учёных[23], в которой они строят графики loss'a между и и угла между направлениями градиента в моменты времени и . Оказывается, что в начале обучения градиенты соседних шагов направлены примерно в одну сторону и функция ошибки убывает монотонно, но с некоторого момента времени в промежутках между и начинает демонстрировать характерные минимумы, а угол между градиентами стремиться к ~170 градусам. Действительно очень похоже, что градиентный спуск «отскакивает» от стен «седла» с маленьким уклоном! Картина намного чище, когда градиентный спуск ведётся с использованием всего датасета; использование minibatch'ей искажает картину до неузнаваемости, что логично. Learning rate не влияет на график угла, а вот размер batch'ей — очень даже. Пересечения локальных минимумов исследователи не обнаружили.

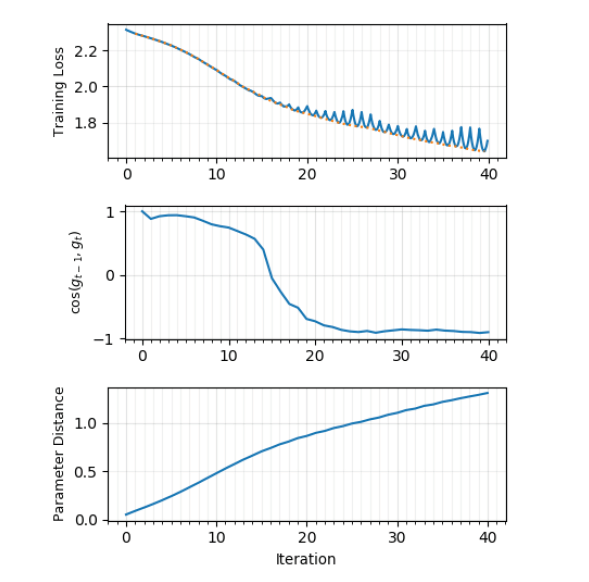
До сих пор мы полагали, что качество найденного минимума зависит только от его глубины. Однако, многие исследователи обращают внимание, что также имеет значение и ширина минимума. Формально её можно определить по-разному; не буду приводить различные формулировки (см. [20], если всё-таки хотите их увидеть), тут достаточно понимать основную мысль. Вот иллюстрация:

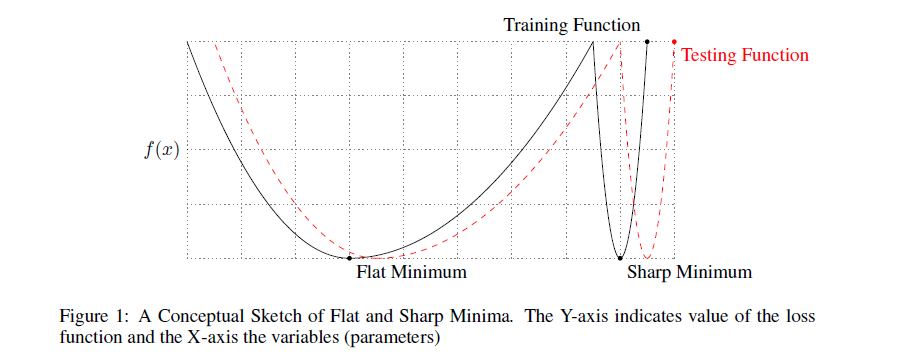
Минимум чёрного графика слева — широкий, справа — узкий. Почему это имеет значение? Распределение тренировочных данных не точно совпадает с распределением тестовых. Можно предположить, что минимумы на тестовых данных будут выглядеть слегка отлично от минимумов исходной функции , в частности, минимумов скорее всего будут смещены друг относительно друга. Но если широкому минимуму такие искажения не страшны, то узкий может измениться до неузнаваемости. Опять таки, обратимся к картинке сверху. Если принять, что чёрный график — исходная , а красный — тестовая, то сразу видно, к каким проблемам это может привести.

Замечено на практике, что градиентный спуск с большими batch'ами систематически достигает немного более хороших результатов на тренировочной выборке, но проигрывает на тестовой. Это часто объясняется тем, что маленькие batch'и вносят шум в оценку целевого распределения и не дают осесть в узком минимуме[21]. Происходит примерно то же самое, что и на картинке выше: функция постоянно меняется (на этот раз намеренно), и на месте ложбин образуются гребни. Из узких впадин при таком «шевелении» выбрасывается, а из широких — нет. Также авторы [21] утверждают, что при обучении с маленьким размером подвыборки убегает значительно дальше от точки инициализации, чем в обратном случае. Такой показатель описывается термином «исследовательская способность алгоритма градиентного спуска», и тоже считается благоприятным для достижения хороших результатов.

Увы, не всё так просто. Мы сталкиваемся с проблемой, упомянутой выше: ширина минимума зависит от параметризации[20]. В сетях с ReLu-активациями достаточно просто построить пример, когда два набора весов и представляют по сути одну и ту же сеть, но — узкий минимум, а — широкий. Более конкретный пример можно увидеть в [13], где узкий и широкий минимумы на графике интерполяции loss'a меняются местами при включении регуляризации:

Возможно, именно с этим связан весьма скромный успех модификации SGD, направленной на то, чтобы направлять оптимизацию в широкие ложбины[22]. Весьма именитые учёные демонстрируют правдоподобные гистограммы гессианов, но прирост в качестве остаётся почти незаметным.

Перекрёстное сравнение

Итак, что мы имеем?

Теоретические работы Chromanska[5], Kawaguchi[8] и Yun[14] согласуются друг с другом. Линейные нейросети — простой частный случай, и вполне логично, что вместо внутренней зоны сложного ландшафта мы получаем один чистый глобальный минимум (при том, что и там и там присутствует «зона сёдел»). В [14] же задаются гораздо более сильные условия на входную функцию.

Связь теории с практикой:

1. Утверждения Chromanska о сложном ландшафте в подпространстве минимумов согласуются с работами по построению низкоэнергетических кривых между минимумами [17][18][19], которые, в свою очередь, согласуются c эмпирическим успехом snapshot-ансамблей[24]. В [19] теоретизируется, что обилие «нор» между минимумами это следствие избыточной параметризации сети, а большое количество весов — основная предпосылка в [5].
2. Утверждение Chromanska о «слоях» в пространстве весов напрямую подтверждаются гистограммами собственных значений гессианов, в особенности, графиками из [3]: почти прямые линии демонстрируют сильную связь между количеством направлений побега и loss'ом.
3. Из теоретических работ напрямую следует поведение полученное в [23], а именно характерное «отскакивание» от стенок ложбины.
4. Утверждения о примерной равноценности минимумов согласуются с практическими результатами (сильно ли разнятся loss'ы среди первых десяти мест в типичном каггельном соревновании?), но косвенно антикоррелируют с анализом, какие фичи выучиваются в разные прогоны обучения[25]. Пока неясно, как всё это соотносится с проблемой узких/широких минимумов.
5. [12] и [11], которые согласуются с [8] и [14], сами по себе хорошо соотносятся с опытом применения residual learning на практике, а также подтверждаются визуализациями в [13].
6. Все вышеперечисленные утверждения совпадают с общими наблюдениями, что даже обычный SGD без накопления импульса стабильно даёт результат не сильно хуже, чем Adam и другие адаптивные алгоритмы градиентного спуска[26][27]. Если бы на пути у SGD встречалось много ловушек, мы бы наблюдали совсем другую картину. Также, если вы запустите обучение сети 100 раз, то скорее всего получите 100 сетей которые выдают примерно одинаковые показатели на валидационной выборке. У вас почти наверняка не будет резких скачков вниз или вверх, что соответствовало бы найденному плохому или, наоборот, слишком хорошему минимуму.
7. Во многих работах уточняется, что хоть теоретический анализ полагается на избыточное количество весов, для работы нейросети большая их часть не нужна. «Лишние» веса выполняют другие функции: во-первых, они «берут на себя» полезные сигналы, позволяя перестраиваться нейронам, которые уже несут положительную нагрузку[19], во-вторых, благодаря им в ландшафте целевой функции образуются хорошие пути спуска[32] (сравните с графиками для вариационной оптимизации в [31]), а в-третьих, благодаря им при инициализации сеть с большей вероятностью окажется в области весов, откуда оптимизация вообще начнётся[33]. Утверждение об избыточности параметризации хорошо коррелирует с успехом работ по сжатию сетей (optimal brain damage, и прочее).

На мой взгляд, остаётся бездоказательным утверждение, что не стоит искать глобальный минимум, потому что он будет иметь такую же обобщающую способность, что и рассеянные вокруг него локальные минимумы. Эмпирический опыт подсказывает, что сети, полученные разными запусками одного и того же минимизатора, делают ошибки на разных элементах (см. графики диссонанса, например, в [16] или в любой работе, посвящённой ансамблированию сетей). То же самое говорят работы по анализу выученных фич. В [25] защищается точка зрения, что большинство самых полезных фич стабильно выучиваются, но часть вспомогательных — нет. Если скомпоновать все редко появляющиеся фильтры, должно стать лучше? Снова вспомним про ансамбли, состоящие из различных версий одной и той же модели[24] и избыточность весов в нейронной сети[28]. Это вселяет уверенность, что всё-таки как-то можно взять лучшее от каждого запуска модели и намного улучшить предсказания, не меняя саму модель. Если ландшафт в сгустке минимумов действительно неисправимо непроходим для градиентного спуска, мне кажется, по его достижении можно попробовать переключиться с SGD на эволюционные стратегии[31] или что-то подобное.

Впрочем, это тоже лишь бездоказательные мысли. Возможно, действительно, не стоит искать чёрную кошку в чёрном миллиономерном гиперпространстве, если её там нет; что глупо бороться за пятые знаки после запятой в лоссе. Чёткое осознание этого дало бы научному сообществу толчок сконцентрироваться на новых архитектурах сетей. ResNet хорошо зашёл, почему нельзя придумать ещё что-то? Также не стоит забывать про пред- и постобработку данных. Если есть возможность преобразовать , чтобы «оголить» подлежащую складку распределения, то не стоит ей пренебрегать.

Куда, на мой взгляд, сообществу учёных следует двигаться дальше?

1. Нужно пробовать новые модифицированные методы градиентного спуска, которые хорошо умеют пересекать местность с седловыми точками. Желательно, методы первого порядка, с гессианом любой дурак сможет. На эту тему уже есть работы с симпатично выглядящими графками[29][30], но в этой области исследований ещё много низковисящих фруктов.
2. Хотелось бы больше знать про подпространство минимумов. Каковы его свойства? Можно ли, получив достаточное количество локальных минимумов, прикинуть, где будет находиться глобальный, или хотя бы более качественный локальный?
3. Теоретические исследования сконцентрированы, в основном, на L2-loss'e. Интересно было бы увидеть, как влияет на ландшафт кросс-энтропия.
4. Неясна ситуация с широкими/узкими минимумами.
5. Остаётся открытым вопрос про качество глобального минимума.

Если среди читателей есть студенты, которым скоро защищать диплом в области машинного обучения, я бы посоветовал им попробовать на зуб первую задачу. Если знаешь, в какую сторону смотреть, гораздо легче придумать что-нибудь здоровское. Также интересно попробовать реплицировать работу LeCun[34], варьируя входные данные.

На этом у меня пока всё. Следите за событиями в научном мире.

Список литературы

[1] Blum, A. L. and Rivest, R. L.; Training a 3-node neural network is np-complete; 1992.
[2] Saxe, McClelland & Ganguli; Exact solutions to the nonlinear dynamics of learning in deep linear neural networks; 19 Feb 2014. (305 цитат на Google Scholar)
[3] Yann N. Dauphin et al; Identifying and attacking the saddle point problem in high-dimensional non-convex optimization; 10 Jun 2014 (372 циатат на Google Scholar, обратите внимание на эту статью)
[4] Alan J. Bray and David S. Dean; The statistics of critical points of Gaussian fields on large-dimensional spaces; 2007
[5] Anna Choromanska et al; The Loss Surfaces of Multilayer Networks; 21 Jan 2015 (317 цитат на Google Scholar, обратите внимание на эту статью)
[6] Anna Choromanska et al; Open Problem: The landscape of the loss surfaces of multilayer networks; 2015
[7] Grzegorz Swirszcz, Wojciech Marian Czarnecki & Razvan Pascanu; Local Minima in Training of Neural Networks; 17 Feb 2017
[8] Kenji Kawaguchi; Deep Learning without Poor Local Minima; 27 Dec 2016. (70 цитат на Research Gate, обратите внимание на эту статью)
[9] Baldi, Pierre, & Hornik, Kurt; Neural networks and principal component analysis: Learning from examples without local minima; 1989.
[9] Haihao Lu & Kenji Kawaguchi; Depth Creates No Bad Local Minima; 24 May 2017.
[11] Moritz Hardt and Tengyu Ma; Identity matters in deep learning; 11 Dec 2016.
[12] A. Emin Orhan, Xaq Pitkow; Skip Connections Eliminate Singularities; 4 Mar 2018
[13] Hao Li, Zheng Xu, Gavin Taylor, Christoph Studer, Tom Goldstein; Visualizing the Loss Landscape of Neural Nets; 5 Mar 2018 (обратите внимание на эту статью)
[14] Chulhee Yun, Suvrit Sra & Ali Jadbabaie; Global Optimality Conditions for Deep Neural Networks; 1 Feb 2018 (обратите внимание на эту статью)
[15] Kkat; Fallout: Equestria; 25 Jan, 2012
[16] Daniel Jiwoong Im, Michael Tao and Kristin Branson; An Empirical Analysis of Deep Network Loss Surhaces.
[17] C. Daniel Freeman; Topology and Geometry of Half-Rectified Network Optimization; 1 Jun 2017.
[18] Timur Garipov, Pavel Izmailov, Dmitrii Podoprikhin, Dmitry Vetrov, Andrew Gordon Wilson; Loss Surfaces, Mode Connectivity, and Fast Ensembling of DNNs; 1 Mar 2018
[19] Felix Draxler, Kambis Veschgini, Manfred Salmhofer, Fred A. Hamprecht; Essentially No Barriers in Neural Network Energy Landscape; 2 Mar 2018 (обратите внимание на эту статью)
[20] Laurent Dinh, Razvan Pascanu, Samy Bengio, Yoshua Bengio; Sharp Minima Can Generalize For Deep Nets; 15 May 2017
[21] Nitish Shirish Keskar, Dheevatsa Mudigere, Jorge Nocedal, Mikhail Smelyanskiy and Ping Tak Peter Tang; On Large-batch Training for Deep Learning: Generalization Gap and Sharp Minima; 9 Feb 2017
[22] Pratik Chaudhari, Anna Choromanska, Stefano Soatto, Yann LeCun, Carlo Baldassi, Christian Borgs, Jennifer Chayes, Levent Sagun, Riccardo Zecchina; Entropy-SGD: Biasing Gradient Descent into Wide Valleys; 21 Apr 2017
[23] Chen Xing, Devansh Arpit, Christos Tsirigotis, Yoshua Bengio; A Walk with SGD; 7 Mar 2018
[24] habrahabr.ru/post/332534
[25] Yixuan Li, Jason Yosinski, Jeff Clune, Hod Lipson, & John Hopcroft; Convergent Learning: Do Different Neural Networks Learn the Same Representations? 28 Feb 2016 (обратите внимание на эту статью)
[26] Ashia C. Wilson, Rebecca Roelofs, Mitchell Stern, Nathan Srebro and Benjamin Recht; The Marginal Value of Adaptive Gradient Methods in Machine Learning
[27] shaoanlu.wordpress.com/2017/05/29/sgd-all-which-one-is-the-best-optimizer-dogs-vs-cats-toy-experiment
[28] Misha Denil, Babak Shakibi, Laurent Dinh, Marc'Aurelio Ranzato, Nando de Freitas; Predicting Parameters in Deep Learning; 27 Oct 2014
[29] Armen Aghajanyan; Charged Point Normalization: An Efficient Solution to the Saddle Point Problem; 29 Sep 2016.
[30] Haiping Huang, Taro Toyoizumi; Reinforced stochastic gradient descent for deep neural network learning; 22 Nov 2017.
[31] habrahabr.ru/post/350136
[32] Quynh Nguyen, Matthias Hein; The Loss Surface of Deep and Wide Neural Networks; 12 Jun 2017
[33] Itay Safran, Ohad Shamir; On the Quality of the Initial Basin in Overspecified Neural Networks; 14 Jun 2016
[34] Levent Sagun, Leon Bottou, Yann LeCun; Eigenvalues of the Hessian in Deep Learning: Singularity and Beyond; 5 Oct 2017

Автор: Павел Садовников

Источник