Слышали ли вы об «эффекте Даннинга-Крюгера»? Это (очевидная) тенденция неквалифицированных людей переоценивать свою компетентность. Обнаруженный в 1999 году психологами Джастином Крюгером и Дэвидом Даннингом эффект с тех пор стал очень знаменитым.
И вы понимаете почему.
Это слишком сочная идея, чтобы не быть правдой. Все «знают», что идиоты, как правило, не осознают своего идиотизма. Или, как выразился Джон Клиз :
Если ты очень-очень глуп, как ты можешь осознать, что ты очень-очень глуп?
Разумеется, психологи очень осмотрительны, что бы убеждаться, что доказательства воспроизводимы. Но, конечно же, каждый раз, когда вы их ищете, из данных выскакивает сам эффект Даннинга-Крюгера. Таким образом кажется, что все стоит на прочной основе.
Вот только есть проблема.
Эффект Даннинга-Крюгера также возникает из данных, в которых его не должно быть. Например, если вы тщательно обработаете случайные данные так, чтобы они не содержали эффекта Даннинга-Крюгера, вы все равно обнаружите этот эффект . Причина оказывается до неприличия простой: эффект Даннинга-Крюгера не имеет ничего общего с человеческой Эффект Даннинга-Крюгера ничего не говорит нам о людях, которых он якобы измеряет. Но он говорит нам о психологии социальных ученых, которые, по-видимому, испытывают трудности со статистикой. </p>" data-abbr="психологией">психологией. Это статистический артефакт — потрясающий пример автокорреляции.
Что такое автокорреляция?
Автокорреляция возникает, когда вы коррелируете переменную саму с собой. Например, если я измерю рост 10 человек, я обнаружу, что рост каждого человека идеально коррелирует сам с собой. Если это звучит как замкнутый круг рассуждений, то это потому, что так оно и есть. Автокорреляция — это статистический эквивалент утверждения, что 5 = 5.
В такой формулировке идея автокорреляции звучит абсурдно. Ни один компетентный учёный не станет соотносить переменную саму с собой. И это верно для чистой автокорреляции. Но что, если переменная окажется в обеих частях уравнения и забудется? В этом случае автокорреляцию обнаружить труднее.
Вот пример. Предположим, я работаю с двумя переменными: x и y . Я обнаружил, что эти переменные совершенно не коррелируют, как показано на левой панели рисунка 1. Пока всё нормально.
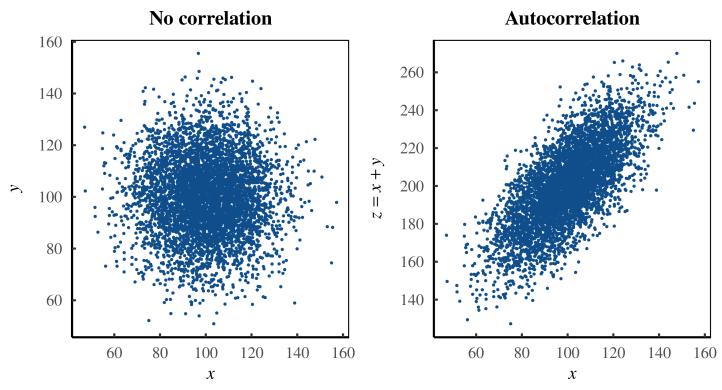
Далее я начинаю играть с данными. После некоторых манипуляций я получил величину, которую называю z. Я сохраняю свою работу и забываю о ней. Несколько месяцев спустя мой коллега вновь обращается к моему набору данных и обнаруживает, что z сильно коррелирует с x (рис. 1 , справа). Мы обнаружили кое-что интересное!
Фактически мы обнаружили автокорреляцию. Видите ли, без ведома моего коллеги я определил переменную z как сумму x + y . В результате, когда мы коррелируем z с x , мы на самом деле коррелируем x сам с собой. (Переменная y появляется в процессе, обеспечивая статистический шум.) Именно так происходит автокорреляция — забывая, что у вас есть одна и та же переменная по обе стороны корреляции.
Эффект Даннинга-Крюгера
Теперь, когда вы понимаете автокорреляцию, давайте поговорим об эффекте Даннинга-Крюгера. Как и в примере на рисунке 1, эффект Даннинга-Крюгера представляет собой автокорреляцию. Но вместо того, чтобы скрываться в измененной переменной, автокорреляция Даннинга-Крюгера скрывается под Кажется очевидным, что Даннинг и Крюгер не намеревались вводить в заблуждение. Скорее, похоже, что они сами обманули себя (и многих других). В этой связи мне стыдно признать, что я читал статью Даннинга и Крюгера несколько лет назад и не заметил ничего неправильного. Я понял это только после прочтения блога Джонатана Джарри. Это стыдно, потому что основной темой этого блога было то, как я указывал на то, что экономисты прибегают к автокорреляции, когда тестируют свои теории стоимости. (Примеры <a href="https://economicsfromthetopdown.com/2022/04/08/the-dunning-kruger-effect-is-autocorrelation/#fn2">https://economicsfromthetopdown.com/2022/04/08/the-dunning-kruger-effect-is-autocorrelation/#fn2</a>) Но меня утешает, что многие ученые также были обмануты диаграммой Даннинга-Крюгера</p>" data-abbr="обманчивой ">обманчивой диаграммой.
Давайте посмотрим.
В 1999 году Даннинг и Крюгер сообщили о результатах простого эксперимента. Они попросили группу людей пройти тест на навыки. (На самом деле Даннинг и Крюгер использовали несколько тестов, но это не имеет значения для моего обсуждения.) Затем они попросили каждого человека оценить свои способности. Даннинг и Крюгер (думали, что они) обнаружили, что люди, плохо сдавшие тест на навыки, также склонны переоценивать свои способности. Это «эффект Даннинга-Крюгера».
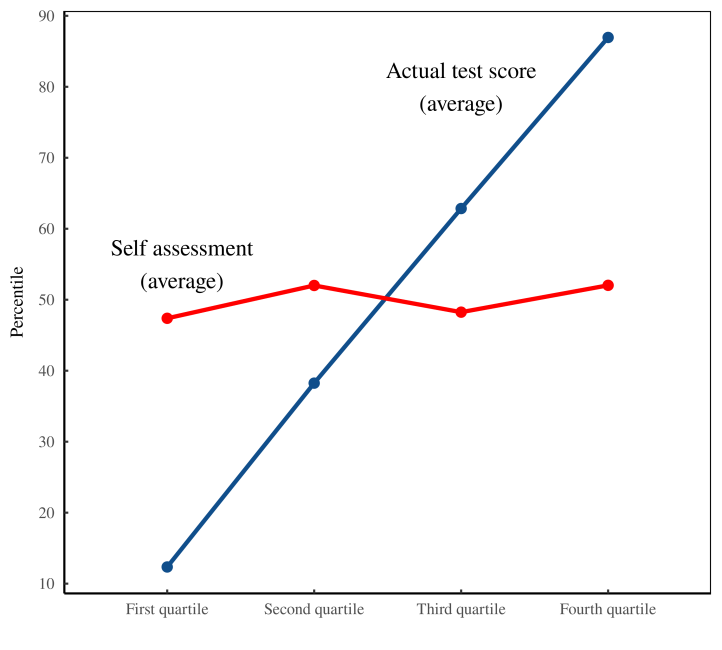
Даннинг и Крюгер визуализировали свои результаты, как показано на рисунке 2. Это простой график, который обращает внимание на разницу между двумя кривыми. На горизонтальной оси ученые распределили людей на четыре группы (квартили) в соответствии с их результатами тестов. На графике две линии показывают результаты внутри каждой группы. Серая линия обозначает средние результаты людей по тесту навыков. Черная линия указывает на их средние «воспринимаемые способности». Очевидно, что люди, получившие плохие результаты на тесте на навыки, слишком самоуверенны в своих способностях. (Или так кажется.)
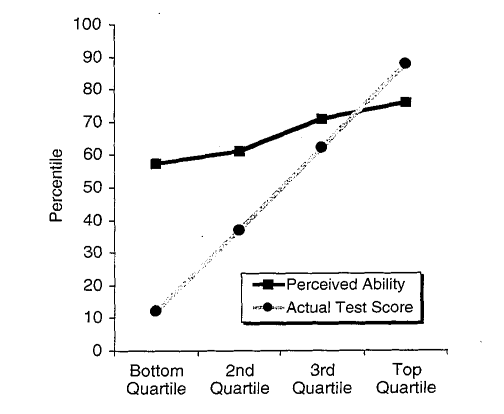
Сама по себе диаграмма Даннинга-Крюгера кажется убедительной. Добавьте к этому тот факт, что эти учёные — превосходные писатели, и вы получите рецепт хитовой статьи. В связи с этим я рекомендую вам прочитать их статью, поскольку она напоминает нам, что хорошая риторика — это не то же самое, что хорошая наука.
Разоблачение Даннинга-Крюгера
Теперь, когда вы ознакомились с диаграммой Даннинга-Крюгера, давайте покажем, как она скрывает автокорреляцию. Чтобы внести ясность, я буду комментировать диаграмму по ходу дела.
Начнем с горизонтальной оси. На диаграмме она является «категориальной», то есть на ней показаны «категории», а не числовые значения. Конечно, нет ничего плохого в использовании категорий. Но в данном случае категории на самом деле числовые. Даннинг и Крюгер берут результаты тестов людей и распределяют их по 4 ранжированным группам. (Статистики называют эти группы «квартилями».)
Это ранжирование означает, что горизонтальная ось эффективно отображает результаты тестов. Назовем эту оценку x .
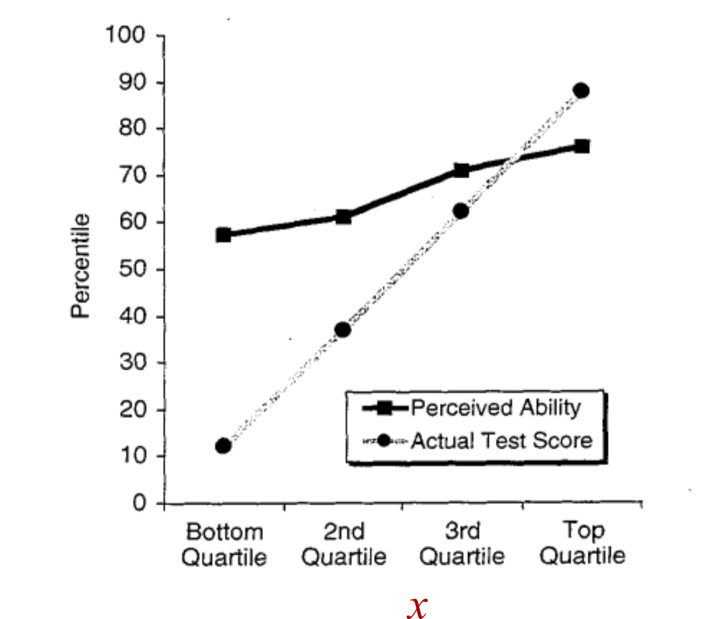
Далее давайте посмотрим на вертикальную ось, которая отмечена «процентилем» (Percentile). Это означает, что вместо того, чтобы отображать фактические результаты тестов, Даннинг и Крюгер строят рейтинг результатов по 100-балльной Преобразование в процентили вводит второе искажение (помимо проблемы автокорреляции). По определению, процентили имеют нижний порог (0) и верхний порог (100) и равномерно распределены между этими границами. Если вы близки к нижнему порогу, вам невозможно занизить свою оценку. Поэтому 'некомпетентные' будут казаться слишком уверенными в себе. И если вы близки к верхнему порогу, вы не можете завысить свою оценку. Следовательно, 'компетентные' будут казаться слишком скромными. См. подробнее в работе Нуфера и других (2016). </p>" data-abbr="шкале">шкале.
Теперь посмотрим на кривые. В строке с надписью «текущий результат теста» (Actual Test Score) отображается средний процентиль результатов теста каждого квартиля (я знаю, что это непростая задача). Кажется, все в порядке, пока мы не осознаем, что Даннинг и Крюгер, по сути, строят график результатов теста ( x ) против самого В технических терминах, Даннинг и Крюгер сопоставляют два различных вида ранжирования — 'процентиль' по баллам теста и 'квартиль' по баллам теста. Неочевидно, что такой тип графика не зависит от данных. По определению, каждый квартиль содержит 25 процентилей, чье среднее значение соответствует середине квартиля. Следствием этой истины является то, что линия, помеченная как 'фактический тестовый балл', парадоксальным образом не говорит нам ничего о фактических баллах людей за тест. </p>" data-abbr="себя">себя. Заметив этот факт, давайте переименуем серую линию. Он эффективно строит график зависимости x от x.
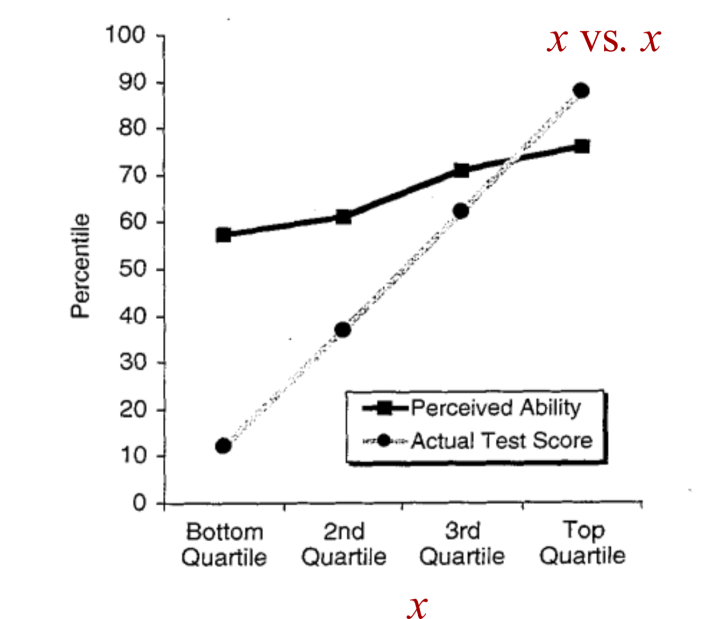
Двигаемся дальше, давайте посмотрим на линию «воспринимаемая способность» (Perceived Ability). Она отображает средний процентиль самооценки каждой группы. Назовем это самооценкой и. Вспоминая, что мы обозначили «фактический результат теста» как x , мы видим, что черная линия отображает зависимость y от результата x.
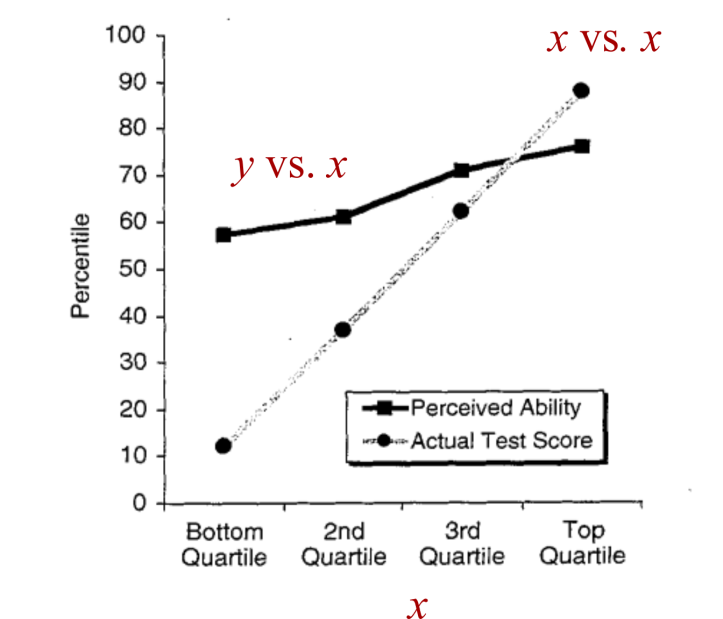
Пока ничего явно неправильного не выскакивает. Да, немного странно строить график x vs. x, но учёные не утверждают, что важна линия сама по себе. Что важно, так это разница между двумя строками («воспринимаемые способности» и «действительный результат теста»). Именно в этой разнице и проявляется автокорреляция.
В математических терминах «разница» означает «вычитание». Таким образом, показывая нам две расходящиеся линии, Даннинг и Крюгер (неявно) просят нас вычесть одну из другой: взять «воспринимаемые способности» и вычесть «действительный результат теста». В моих обозначениях это соответствует y – x .
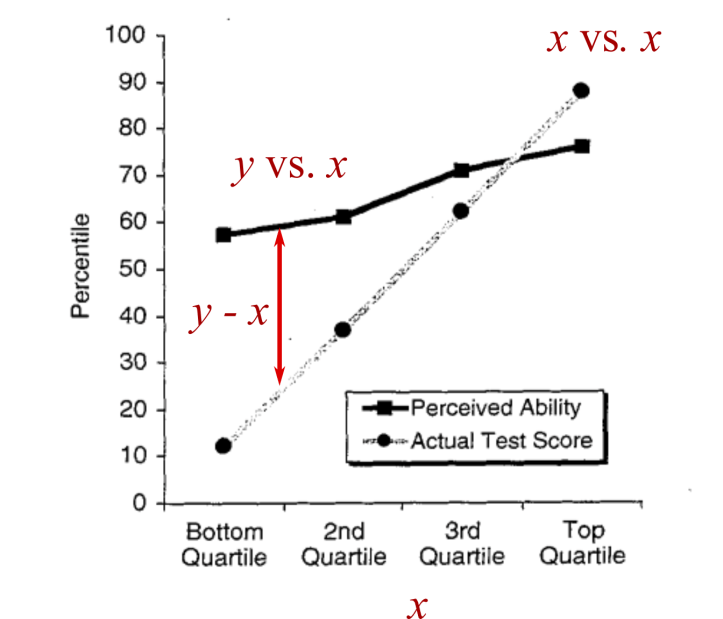
Вычитание y – x кажется вполне приемлемым, пока мы не осознаем, что должны интерпретировать эту разницу как функцию горизонтальной оси. Но по горизонтальной оси отложен результат теста x . Итак, нас (неявно) просят сравнить y – x с x :
(y−x) ∼ x
Видите проблему? Мы сравниваем x с его отрицательной версией. Это автокорреляция по учебнику. Это значит, что мы можем бросать случайные числа в x и y — такие, которые не содержат эффект Даннинга-Крюгера — и, тем не менее, на другом конце эффект все равно возникнет.
Воспроизведение эффекта Даннинга-Крюгера
Честно говоря, меня не особо убедили приведенные выше аналитические аргументы. Только используя реальные данные, я пойму проблему эффекта Даннинга-Крюгера.
Предположим, мы психологи, получившие крупный грант на повторение эксперимента Даннинга-Крюгера. Мы набираем 1000 человек, тестируем каждого из них и просим их пройти самооценку. Когда результаты будут получены, мы посмотрим на данные.
И выглядит это не очень хорошо.
Когда мы сопоставляем результаты тестов людей с их самооценкой, данные кажутся совершенно случайными. На рисунке 7 показан паттерн. Кажется, что люди с любыми способностями одинаково плохо предсказывают свои навыки. Нет и намека на эффект Даннинга-Крюгера.
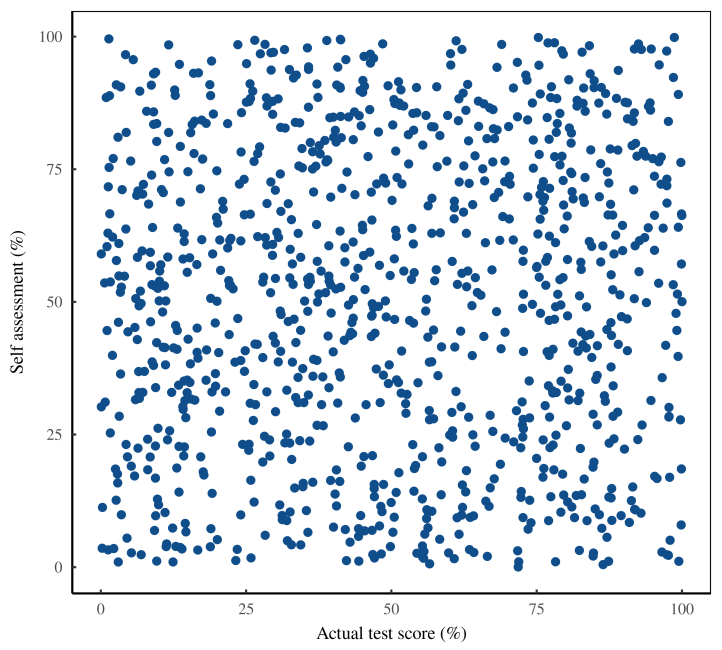
Посмотрев на наши необработанные данные, мы обеспокоены, что сделали что-то не так. Многие же другие исследователи повторили эффект Даннинга-Крюгера. Допустили ли мы ошибку в нашем эксперименте?
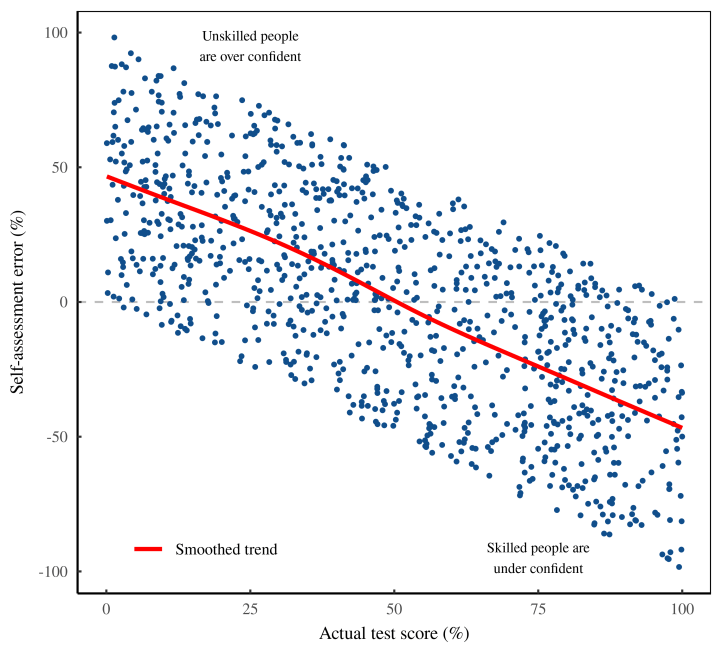
К сожалению, мы не можем собрать больше данных — у нас закончились деньги. Но мы можем поиграть с анализом. Коллега предлагает вместо построения необработанных данных рассчитать «ошибку самооценки» каждого человека. Эта ошибка представляет собой разницу между самооценкой человека и его результатом теста. Возможно, эта ошибка оценки связана с фактическим результатом теста?
Мы подсчитали цифры и, к нашему изумлению, обнаружили огромный эффект. На рисунке 8 показаны результаты. Кажется, что неквалифицированные люди чрезвычайно самоуверенны, а квалифицированные — чрезмерно скромны.
(Наши лабораторные специалисты отмечают, что корреляция на удивление тесная, как если бы числа были выбраны вручную. Но мы выбрасываем это наблюдение из головы и идем вперед.)
Воодушевленные успехом, мы решаем, что результаты, возможно, в конце концов не будут «плохими». Итак, мы строим диаграмму Даннинга-Крюгера, чтобы посмотреть, что произойдет. Мы обнаружили, что, несмотря на наши опасения по поводу данных, эффект Даннинга-Крюгера существовал всегда. На самом деле, как показано на рисунке 9, наш эффект даже больше, чем исходный.
Все идет под откос
Довольные нашим успешным воспроизведением, мы начинаем описывать наши результаты. И потом все разваливается. Охваченный чувством вины, наш дата инженер признается: он потерял данные нашего эксперимента и в приступе паники заменил их случайными числами. Наши результаты, признается он, основаны на статистическом шуме.
Опустошенные, мы возвращаемся к нашим данным, чтобы понять, что пошло не так. Если бы мы работали со случайными числами, как бы мы смогли воспроизвести эффект Даннинга-Крюгера? Чтобы выяснить, что произошло, мы перестаём притворяться, что работаем с психологическими данными. Мы переименовываем наши диаграммы в терминах абстрактных переменных x и y. Сделав это, мы обнаруживаем, что наш очевидный «эффект» на самом деле является автокорреляцией.
Рисунок 10 объясняет это. Наш набор данных состоит из статистического шума — двух случайных величин x и y, которые совершенно не связаны между собой (рис. 10 А). Когда мы вычисляли «ошибку самооценки», мы брали разницу между y и x . Неудивительно, что мы обнаружили, что эта разница коррелирует с x (рис. 10 B). Но это потому, что x автокоррелирует сам с собой. Наконец, мы разбираем диаграмму Даннинга-Крюгера и понимаем, что она тоже основана на автокорреляции (рис. 10 C). Он просит нас интерпретировать разницу между y и x как функцию x . Это автокорреляция из графика B, обернутая в более обманчивую оболочку.
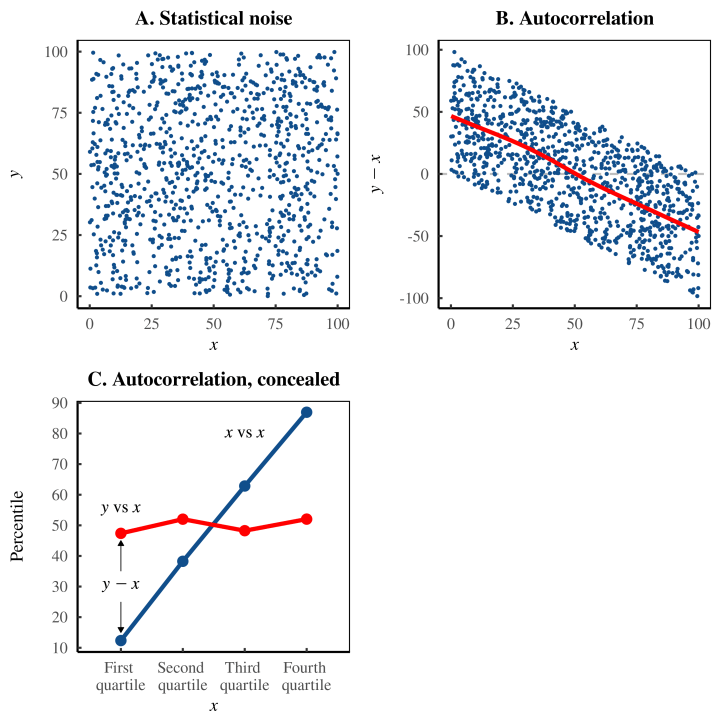
Цель этой истории — продемонстрировать, что эффект Даннинга-Крюгера не имеет ничего общего с человеческой психологией. Это статистический артефакт — пример автокорреляции, скрывающийся на виду.
Что интересно, так это то, сколько времени потребовалось исследователям, чтобы осознать ошибку в анализе Даннинга и Крюгера. Даннинг и Крюгер опубликовали свои результаты в 1999 году. Но только в 2016 году ошибка была полностью понята. Насколько мне известно, Эдвард Нухфер и его коллеги были первыми, кто исчерпывающе развенчал эффект Даннинга-Крюгера. (См. их совместные статьи в 2016 и 2017 годах .) В 2020 году Жиль Жиньяк и Марсен Заженковски опубликовали аналогичную критику .
Как только вы прочитаете эту критику, станет до боли очевидно, что эффект Даннинга-Крюгера является статистическим артефактом. Но на сегодняшний день об этом факте мало кто знает. В совокупности три критические статьи цитируются примерно в 90 раз меньше , чем Согласно Google Scholar, три критические работы (Нуфера 2016, 2017 и Гиньяка и Заенковского 2020) в сумме имеют 88 цитирований. В отличие от этого, работа Даннинга и Крюгера (1999) имеет 7893 цитирования. </p>" data-abbr="оригинальная ">оригинальная статья Даннинга-Крюгера. Таким образом, похоже, что большинство учёных до сих пор считают, что эффект Даннинга-Крюгера является Медленное распространение 'опровержений' является общей проблемой в науке. Даже когда первоначальные (неверные) статьи отзываются, они часто продолжают накапливать цитирования. Кроме того, статьи с критикой редко публикуются в том же журнале, что и оригинальная статья. Таким образом, ошибочная статья в Nature, скорее всего, будет опровергнута в более малоизвестном журнале. Эта асимметрия частично объясняет, почему я пишу об эффекте Даннинга-Крюгера здесь. Я считаю, что критика, высказанная Нуфером и другими (а также Гиньяком и Заенковским), заслуживает широкой известности (прим. пер. пер. —в том числе перевода) </p>" data-abbr="важным ">важным аспектом человеческой психологии.
Никаких следов эффекта.
Проблема с диаграммой Даннинга-Крюгера заключается в том, что она нарушает фундаментальный принцип статистики. Если вы собираетесь сопоставить два набора данных, их необходимо измерять независимо. В диаграмме этот принцип нарушается. На ней результаты тестов смешиваются по обеим осям, что приводит к автокорреляции.
Осознав эту ошибку, Эдвард Нухфер и его коллеги задали интересный вопрос: что происходит с эффектом Даннинга-Крюгера, если его измерить статистически достоверным способом? По свидетельству Нухфера, ответ заключается в том, что эффект исчезает.
На рисунке 11 показаны их результаты. Здесь важно то, что «навыки» людей измеряются независимо от их результатов на тестах и самооценки. Чтобы измерить «навыки», Нухфер группирует людей по уровню образования, показанному на горизонтальной оси. Затем вертикальная ось отображает ошибку в самооценке людей. Каждая точка представляет отдельного человека.
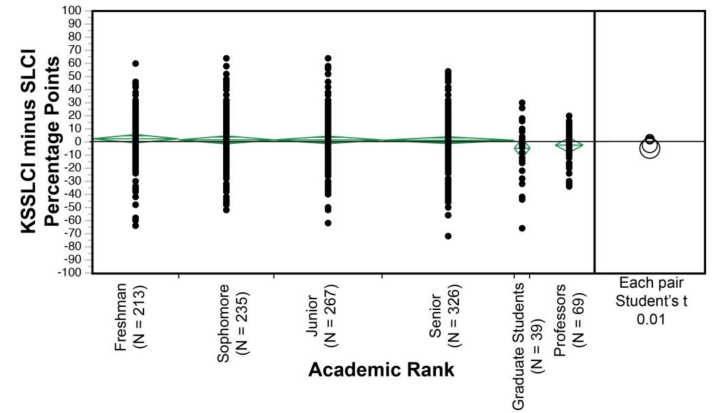
Если бы присутствовал эффект Даннинга-Крюгера, он отобразился бы на рисунке 11 как нисходящая тенденция данных (аналогично тенденции на рисунке 7). Такая тенденция указывает, что неквалифицированные люди переоценивают свои способности, и что эта переоценка уменьшается с увеличением навыков. Глядя на рисунок 11, мы не видим никаких намеков на тенденцию. Вместо этого средняя ошибка оценки (обозначенная зелеными кружками) колеблется около нуля. Другими словами, предвзятость оценки тривиально мала.
Хотя на эффект Даннинга-Крюгера нет никаких намеков, на рис. 11 показана интересная закономерность. Двигаясь слева направо, разброс ошибок самооценки имеет тенденцию уменьшаться по мере повышения уровня образования. Другими словами, преподаватели обычно лучше оценивают свои способности, чем первокурсники. В этом есть смысл. Обратите внимание, однако, что эта возрастающая точность отличается от эффекта Даннинга-Крюгера, который связан с системной погрешностью средней оценки. В данных Нуфера такой предвзятости не существует.
Неквалифицированный и не знающий об этом
Ошибки случаются. Поэтому в этом смысле нам не следует винить Даннинга и Крюгера в допущенных ошибках. Однако в обстоятельствах их ошибки есть восхитительная ирония. Вот два профессора Когда Даннинг и Крюгер опубликовали свою статью в 1999 году, они оба работали в Корнельском университете. </p>" data-abbr="Лиги плюща">Лиги плюща, утверждающие, что неквалифицированные люди несут «двойное бремя»: неквалифицированные люди не только «некомпетентны»… они не осознают своей собственной некомпетентности.
Ирония в том, что ситуация на самом деле обратная. В своей основополагающей статье Даннинг и Крюгер демонстрируют свою (статистическую) некомпетентность, смешивая автокорреляцию с психологическим эффектом. В этом свете название статьи может быть уместным. Просто именно авторы (а не испытуемые) были «неквалифицированными и не подозревали об этом».
Автор:
robertd