Используем силу уравнений Ньютона и численных методов для моделирования динамики простых плоских мешей в реальном времени! В конце вы сможете моделировать падение ножниц ✂️ как на анимации
Рубрика «численное интегрирование»
Реализация базового метода Стёрмера-Верле
2025-05-01 в 15:24, admin, рубрики: jupyterlab, rigid body, SIM, wljs, Wolfram, механика, Ньютоновская механика, пятничное, численное интегрирование, численные методы
Релятивистская трассировка лучей
2025-04-22 в 8:34, admin, рубрики: glsl, OpenGL, sympy, общая теория относительности, трассировка лучей, численное интегрирование
В этой статье я покажу как можно самому, бесплатно и без смс, нарисовать черную дыру при помощи OpenGL, в полном соответствии с ОТО.
Для этого, мы сначала выведем уравнения движения лучей света, напишем интегратор Рунге-Кутты на GLSLЧитать полностью »
Вычисление определённых интегралов: базовые алгоритмы
2018-08-23 в 23:26, admin, рубрики: python, Алгоритмы, математика, численное интегрирование, экстраполяция
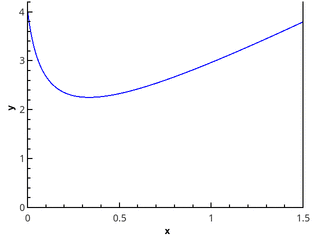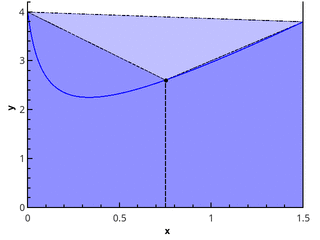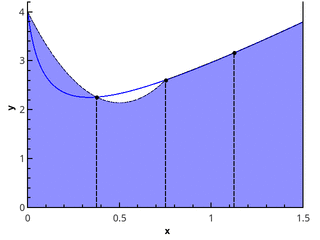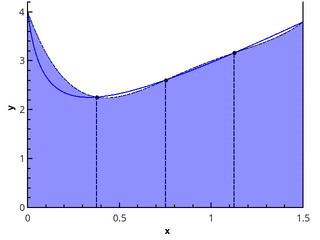
В этой публикации описаны простейшие методы вычисления интегралов функций от одной переменной на отрезке, также называемые квадратурными формулами. Обычно эти методы реализованы в стандартных математических библиотеках, таких как GNU Scientific Library для C, SciPy для Python и других. Публикация имеет целью продемонстрировать, как эти методы работают "под капотом", и обратить внимание на некоторые вопросы точности и производительности алгоритмов. Также хотелось бы отметить связь квадратурных формул и методов численного интегрирования обыкновенных дифференциальных уравнений, о которых хочу написать ещё одну публикацию.
Интегрирование уравнений движения
2017-11-10 в 8:50, admin, рубрики: Алгоритмы, математика, разработка игр, уравнения движения, физика, численное интегрирование, численные методы
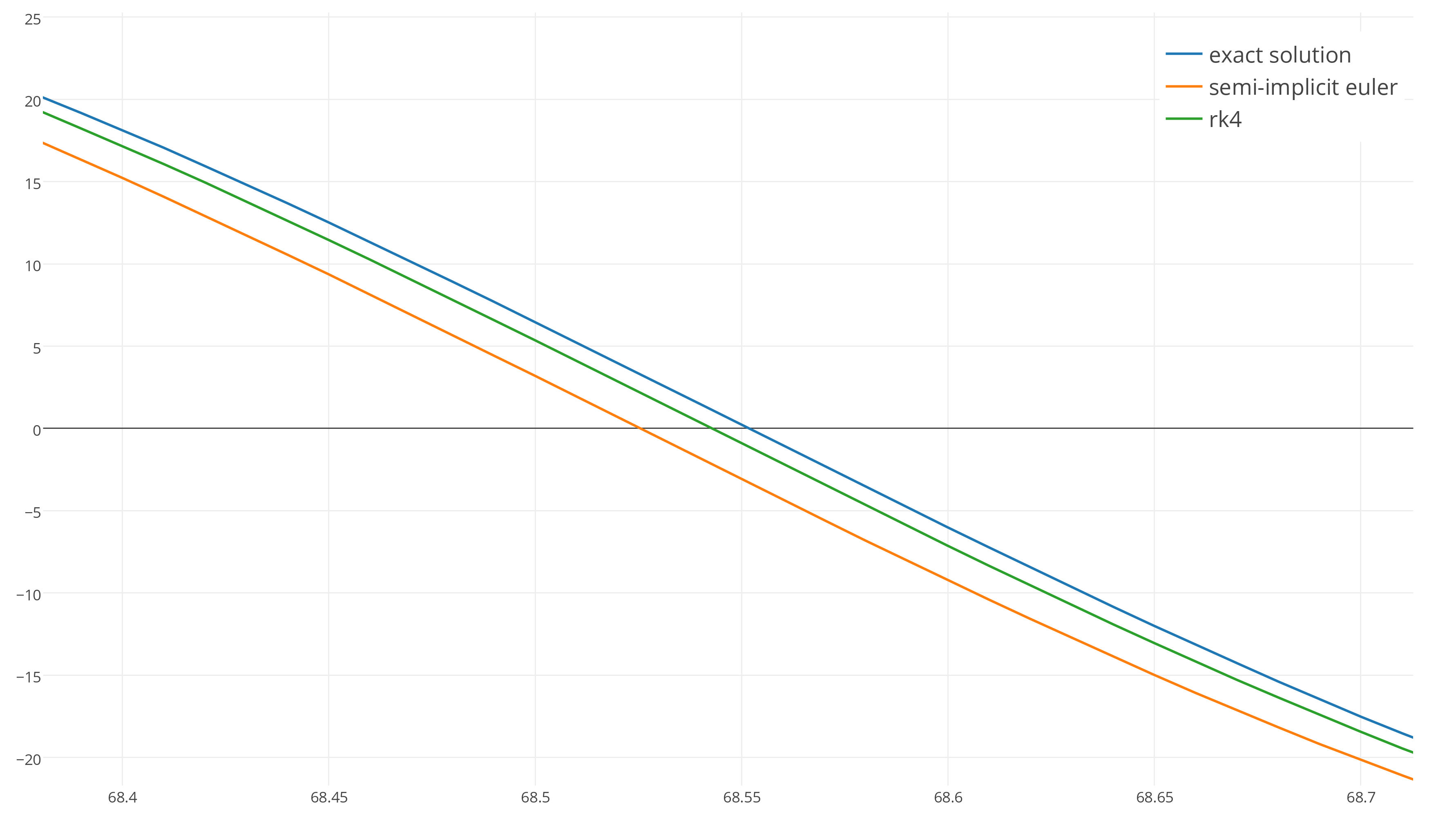
Симуляция физики делает небольшие предсказания на основании законов физики. Эти предсказания на самом деле достаточно просты, что-то вроде «если объект вот здесь и он движется с такой скоростью в этом направлении, то за краткий промежуток времени он окажется вот тут». Мы создаём такие предсказания с помощью математической техники под названием интегрирование.
Темой этой статьи как раз и будет реализация такого интегрирования.
Интегрирование уравнений движения
Вы можете помнить из курса старшей школы или вуза, что сила равна произведению массы на ускорение.
Преобразуем это уравнение и увидим, что ускорение равно силе, делённой на массу. Это соответствует нашим интуитивным ожиданиям, потому что тяжёлые объекты труднее бросать.
Ускорение — это темп изменения скорости от времени:
Аналогично, скорость — это темп изменения позиции от времени:
Это значит, что если мы знаем текущие позицию и скорость объекта, а также приложенные к нему силы, то сможем проинтегрировать, чтобы найти его позицию и скорость в определённый момент времени.
Читать полностью »
Симуляция физического мира
2017-10-02 в 5:58, admin, рубрики: CGI (графика), анимация, веб-дизайн, Компьютерная анимация, математика, Матчасть, прототипирование, симуляция, физика, численное интегрирование, численные методы
Как бы вы подошли к симуляции дождя, ну или любого другого продолжительного физического процесса?
Симуляцию, будь это дождь, поток воздуха над крылом самолёта или же падающий по ступенькам слинки (помните игрушку-пружинку радугу из детства?), можно представить, если знать следующее:
- Состояние всего в момент начала симуляции.
- Как это состояние меняется из одного момента времени в другой?